Показникова функція та її властивості
Узагальнити і систематизувати знання учнів з теми" Пказникова функція, показникові рівняння та нерівност"; формувати в учнів уміння та навички творчого застосування знань і вмінь до розвязування завдань
Урок з теми
«Показникова функція»
Мета: Узагальнити і систематизувати знання учнів з теми « Показникова функція , показникові рівняння та нерівності»; формувати в учнів уміння та навички творчого застосування знань і вмінь до розв′язування завдань; виховувати працелюбність, розвивати прагнення до знань; зацікавити учнів проектом, організувати роботу творчих груп.
Тип уроку: узагальнення та систематизація знань.
Хід уроку
Математику слід вивчати у школі ще й з тією метою, щоб одержані тут знання були достатні для звичайних потреб у житті
Микола Іванович Лобачевський
І. Організаційний момент
ІІ. Повідомлення теми і мети уроку
Учні класу зазделегідь поділені на три групи: «Функція». «Рівняння», « Нерівності». У кожній групі є теоретики, дослідники та практики. Кожна з груп представляє частину теоретичного матеріалу з теми, ілюструє його застосування під час розв′язування завдань.
Учитель повідомляє учням тему й мету уроку , називає групи, напрями їх діяльності.
ІІІ. Мотивація навчальної діяльності
Учитель. А чи не виникало у вас запитання, навіщо потрібно вивчати цю тему?
Чи потрібно вміти розв′язувати показникові рівняння і нерівності?
Де можна використати знання з даної теми?
Наприклад, можна навести багато задач із фізики, біології, економіки, які зводяться до показникових рівнянь. Це і радіоактивний розпад і барометрична формула , і т.д
Сьогодні на уроці ми повторимо основні способи розв′язування показникових рівнянь і які методи застосовують для розв′язування показникових нерівностей.
IV.Актуалізація опорних знань
«Метод мікрофон».
1.Що називається функцією?
2.Що називається областю визначення функції? Навести приклади.
3.Що називається областю значень функції? Навести приклади.
4.Яку функцію називають зростаючою? Навести приклади.
5.Яку функцію називають спадною? Навести приклади.
6.Із усіх запропонованих функцій назвати показникові:
1) f(x) = ![]() ; 2) f(x) =
; 2) f(x) = ![]() ; 3) f(x) =
; 3) f(x) = ![]() ; 4) f(x) =
; 4) f(x) = ![]() ; 5) f(x) =
; 5) f(x) = ![]() ; 6) f(x) =
; 6) f(x) = ![]()
7. При якій основі існує показникова функція.
8.Якою є функція, якщо основа дорівнює 1 і що є графіком даної функції.
9. Порівняти ![]() і
і ![]() , якщо:
, якщо:
А) ![]() >
> ![]() ; б) (
; б) ( ![]() <
< ![]()
10.Які рівняння називають показниковими?
11.Які властивості степенів використовують при розв’язуванні показникових рівнянь?
12.Які існують способи розв’язування показникових рівнянь?
13.Які нерівності називають показниковими?
14.На яких властивостях показникової функції базується розв’язування показникових нерівностей виду ![]() <
< ![]() ( a>0; a
( a>0; a ![]() 1).
1).
15.Які методи застосовуються для розв’язування показникових нерівностей?
V. Узагальнення та систематизація знань.
( Виступи учнів)
Група «Функції»
Теоретик
Доповідає про поняття та властивості функції:
Показникова фукція f(x) = ![]() , де а > 0; а
, де а > 0; а ![]() 1.
1.
- а>1.

Властивості: D(y) : х є R
E(y) : y є (0; ![]() )
)
Якщо х=0, то у = 1.
Функція зростає.
- 0< а < 1
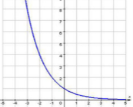
Властивості: D(y) : х є R
E(y) : y є (0; ![]() )
)
Якщо х=0, то у = 1.
Функція спадає.
Дослідник:
При розв’язуванні показникових рівнянь застосовують основні показникові тотожності.
Для а>0, b>0 та будь – яких дійсних x і у справедливі такі рівності:
-
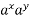 =
=  ; 2)
; 2)  =
=  ; 3)(
; 3)(  =
= 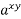 ; 4)(
; 4)(  =
= 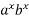 ; 5)(
; 5)(  =
=  .
.
Практик
1.Порівняти a і b, якщо:
-
 ; 2)
; 2) 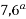 <
<  ; 3)
; 3) 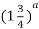 <(
<(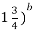 ; 4) (
; 4) (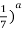 > (
> (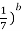 .
.
2. Порівняти із числом 1 значення виразу:
1) ( ![]() ; 2) (
; 2) ( ![]() ; 3) (
; 3) ( ![]() ; 4)
; 4) ![]() .
.
3. Порівняти із числом 1, додатне числом а,
1) ![]() >
> ![]() ; 2)
; 2) ![]()
![]()
![]() ; 3)
; 3) ![]() >
> ![]() ; 4)
; 4) ![]() >
> ![]() .
.
Група «Рівняння»
Теоретик
- Дає визначення, які рівняння називаються показниковими.
- Пояснює, які існують способи розв’язування показникових рівнянь.
Дослідник
-
Зведення обох частин рівняння до виду
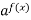 =
=  . Наприклад:
. Наприклад:
а)![]() = (2
= (2![]() ). б)
). б) ![]() ∙
∙![]() = 5∙
= 5∙![]() .
.
2) Винесення спільного множника за дужки. Наприклад:
![]() +
+ ![]() +
+![]() +
+![]() +
+ ![]() =120.
=120.
Практик
3)Заміна змінної, зведення показникових рівнянь до квадратних:
а) ![]() - 8∙
- 8∙![]() - 9 =0;
- 9 =0;
б) ![]() -
- ![]() =99;
=99;
в) 9∙![]() - 7∙
- 7∙![]() - 16∙
- 16∙![]() = 0.
= 0.
Група «Нерівності»
Теоретик
При розв′язуванні показникових нерівностей необхідно враховувати властивості поазникової функції:
-
Якщо 0<а<1
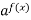 ≤
≤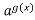 , то f(x) ≥ g(x);
, то f(x) ≥ g(x);
-
Якщо а > 1
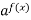 ≤
≤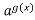 , то f(x)≤ g(x).
, то f(x)≤ g(x).
Дослідник
а) ![]() > 1; б)
> 1; б) ![]() - 4∙
- 4∙![]() +
+ ![]() < 80.
< 80.
Практик
а) ![]() - 6∙
- 6∙![]() ≥ 4; б) 3∙
≥ 4; б) 3∙![]() + 37∙
+ 37∙![]() = 26∙
= 26∙![]() .
.
VI. Підсумок уроку, рефлексія
VII. Домашнє завдання.
1.П.2; № 2.18; № 3.14.
- Додаткове завдання. Розвяжіть рівняння
![]() =
= ![]()
Відповідь: х=2.
![]()


про публікацію авторської розробки
Додати розробку
