Розвязування задач на знаходження первісних
Розвʼязування задач на знаходження первісних
Ванда Пашкова , учитель математики спеціалізованої школиІ – ІІІ ст. № 106,м. Київ
Мета уроку : узагальнити знання учнів про первісну; формувати уміння і навички обчислення первісних.
Розвивати увагу, розумову діяльність, уміння виконувати порівняльний аналіз, спонукати до пізнавальної діяльності; виховувати працьовитість, активність, інтерес до математики.
Тип уроку: узагальнення та систематизація знань.
Обладнання та наочність :презентація в PowerPoint, конверти із завданнями, інтерактивна дошка, мікрофон, робочий зошит.
Хід уроку
І. Організаційний етап
ІІ. Перевірка домашнього завдання.
Розв′язки домашнього завдання записані на слайдах. В кожному з номерів є помилка. Учням необхідно знайти й пояснити де є помилки. Один з учнів пояснює, як треба було розв′язати і чому.
ІІІ. Формування мети й завдань уроку
Учитель. Перш ніж розпочати урок, я хочу звернути вашу увагу на слова, які сказав відомий французський філософ, письменник, фізик, математик Блез Паскаль: «Предмет математики настільки серйозний, що корисно не упускати можливостей робити його цікавішим». Ці рядки залишаються актуальними й нині, тому що знання - це єдиний , цілісний і нерозривний процес, який має початок, але не має кінця…
Сьогодні на уроці ми закріпимо знання про первісну, обчислення первісних.
ІV. Актуалізація опорних знань
Метод «Мікрофон»
( представники кожної команди ставлять по черзі запитання учням інших команд. Якщо учні команди не відповідають на поставлене запитання або дають неправильну відповідь, то запитання адресується учням інших команд).
- Яку функцію називають первісною функціїf на проміжкуI?
- Сформулювати основну властивість первісної.
- Який запис називають загальним виглядом первісних?
- Хто з математиків відкрив інтегральне числення?.
- Які є правила знаходження первісних?
Тестові завдання
-
Яка з наведених функцій є первісною функції f(x)=2
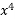
-
F(x)=8
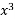 ; Б)F(x) =
; Б)F(x) =  ; B) F(x) =
; B) F(x) = 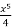 ; Г) F(x) =
; Г) F(x) =  .
.
2).Знайти загальний вигляд первісної функціїf(x)= ![]() + 3.
+ 3.
А) F(x)= 2х +С; Б)F(x) = ![]() ; B) F(x) =
; B) F(x) = ![]() + 3х +С; Г) F(x) = 2х + С.
+ 3х +С; Г) F(x) = 2х + С.
3) Указати загальний вигляд первісної функції у= 2![]() - 4х + 3
- 4х + 3
А) F(x)= 10![]() - 4х+ 3; Б)
- 4х+ 3; Б)![]() - 2
- 2![]() +3х + С; B) F(x) =
+3х + С; B) F(x) =![]() - 4
- 4![]() +3х +С;
+3х +С;
Г) F(x) =![]() - 2
- 2![]() + 3х.
+ 3х.
4) Яка з наведенихфункцій є первісною функції у = ![]() ?
?
А) F(x)= 5tg2x; Б)F(x) = ![]() ; B) F(x) =
; B) F(x) =![]() ; Г) F(x) = 5 tg2x.
; Г) F(x) = 5 tg2x.
5)Для функції f(x) = -2x +4, указати первісну, графік якої проходить через точку А(1; 2).
А. F(x)= -![]() +4х – 1; Б)
+4х – 1; Б) ![]() -
- ![]() +4х +2; В)
+4х +2; В)![]() +3х + 7; Г)
+3х + 7; Г)![]() -
- ![]() -4х -1.
-4х -1.
6)Для функції f(x) = 5+ 6x указати первісну, яка задовольняє дану умову![]() 24.
24.
А. F(x)= 5х +3![]() +12; Б)
+12; Б) ![]() - 5х +3
- 5х +3![]() +24; В)
+24; В)![]() 5+ 6x +12; Г)
5+ 6x +12; Г)![]() +6х +5
+6х +5
Правильнівідповідівідмітьте Х
П.і. учня
|
|
А |
Б |
В |
Г |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
( Учні виконують тести на аркушах, які здають вчителю , а бланки з відповідями залишають у себе для перевірки)
Відповіді: 1. Б; 2 .В; 3. Б; 4. В; 5. А; 6. А.
V. Засвоєння вмінь і навичок
Учитель. Повторення теоретичного матеріалу закінчено. Розглянемо декілька вправ на закріплення правил знаходження первісних.
1. Знайти первісну функції (усно)
1) f(x) = ![]() ; 2) f(x) =
; 2) f(x) =![]() ; 3) f(x) =
; 3) f(x) = ![]() ; 4) f(x) =
; 4) f(x) = ![]() ; 5) f(x) = sin 7x ; 6) f(x) = 4 cos
; 5) f(x) = sin 7x ; 6) f(x) = 4 cos![]()
2.Гра «Вірю - не вірю»
( Учні розв’язують задачі й відповідають за бажанням. Свою відповідь вони починають зі слів «вірю» або не «вірю»)
1) f(x) = 4sin2x; ![]() - 4 cos2x + C.
- 4 cos2x + C.
2) f(x) = - cos ![]() ;
; ![]() sin
sin ![]() + C.
+ C.
3) f(x) =![]() ;
; ![]() + C.
+ C.
4) f(x) = 3![]() ;
; ![]() - 3
- 3![]() + C.
+ C.
3. Для функції знайти первісну, яка задовольняє дану умову:
1) f(x) = 6![]() + 4х -3 , F(-2) = -3.
+ 4х -3 , F(-2) = -3.
2) f(x) =![]() , графік первісної проходить через точку М(-1; -
, графік первісної проходить через точку М(-1; -![]() ).
).
4.Розвʼязати завдання
Точка рухається по прямій так, що її V(t) = 7+2t. Знайдіть шлях, пройдений точкою за проміжок шляху від ![]() =2c до
=2c до ![]() =6c (швидкість руху вимірюється у метрах за секунду)
=6c (швидкість руху вимірюється у метрах за секунду)
VІ. Робота в групах
(Завдання кожної групи – за 15 хв. оперативно та правильно розв’язати завдання. Кожен учень повинен уміти пояснити розв’язання завдання. Представники групи по черзі пояснюють розв′язок певного завдання біля дошки, усі інші учні записують умови та їхні розв′язки в зошит).
Завдання для групи №1
Знайдіть первісну функції, графік якої проходить через вказану точку
-
f(x) =
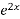 + sinx , A(0;0).
+ sinx , A(0;0).
-
f(x) = 4
 – 5 x + 7 A(1; 3).
– 5 x + 7 A(1; 3).
-
f(x) =
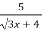 A(4; 7)
A(4; 7)
-
f(x) =
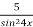 A(
A( ; -
; - )
)
Завдання для групи №2
Знайдіть первісну функції, графік якої проходить через вказану точку
-
f(x) =
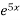 + sinx , A(0;1).
+ sinx , A(0;1).
-
f(x) = 4
 – 5 x + 7 , A(1; 3).
– 5 x + 7 , A(1; 3).
-
f(x) =
 cos
cos +
+  sin
sin , A(
, A( ; -
; - )
)
-
f(x) =
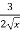 + 1 , A(4; -5)
+ 1 , A(4; -5)
Завдання для групи №3
Знайдіть первісну функції, графік якої проходить через вказану точку
-
f(x) = 2
 A (
A ( ;
;  ).
).
-
f(x) = 4
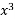 -
-  + 2x – 1, A(1;1).
+ 2x – 1, A(1;1).
-
f(x) =
 cos
cos -
-  sin
sin , A(
, A(  ).
).
-
f(x) =
 -
-  , A(1; -2)
, A(1; -2)
Здати роботи вчителю на перевірку.
VIІ.Підбиття підсумків уроку, рефлексія
Учитель
Які завдання для вас виявилися найважчими?
На які завдання потрібно звернути увагу на наступному уроці?
З якими завданнями було працювати цікаво?
VIII.Домашнє завдання
П.10; №10.10; №10.12.


про публікацію авторської розробки
Додати розробку
