Пошуково-наукова робота "Таємниці усного обчислення"

Сколівська академічна гімназія

 

 

 

 

 

 

 

 

 

 

Тема роботи
Таємниці усного обчислення

Секція природничо-математичних наук

 

 

 

 

 

 

Пошуково-наукова робота

учениці 6(10)-А класу,

Павлишин Ірини

Науковий керівник:

Павлишин Марта Теодорівна

 

 

 

 

 

 

2014-2015 н.р.

 

Я, міркую,  значить я існую

Рене   Декарт

 

Феномен особливих здібностей в усному рахунку зустрічається з давніх-давен. Як відомо, ними володіло  багато вчених, зокрема, Андре Ампер і Карл Гаусс. Проте, вміння швидко обчислювати була властива і тим людям, чия професія була далекою від математики та науки загалом.

До другої половини ХХ століття на естраді були популярними виступи фахівців у усному рахунку. Іноді вони влаштовували показові змагання між собою. Відомими російськими «суперрахівниками» є Арон Чиквашвили, Давид Гольдштейн, Юрій Гірський, зарубіжними: Борислав Гаджански, Вільям Клайн, Томас Фулер та інші.

Хоча окремі фахівці запевняли, що «справа у вроджених здібностях», інші аргументовано доводили зворотнє: «не тільки у якихось виняткових, феноменальних здібностях, а в знанні деяких математичних законів, які дозволяють швидко обчислювати» і з бажанням розкривали ці закони.

Істина, звісно ж, виявилася на певної «золотої середини» поєднання природних здібностей й освіченого, працьовитого їх пробудження, започаткування і використання. Ті, хто слідуючи Трофиму Лисенку, сподіваються виключно на напористість, з усіма його добре відомими способами і прийомами усного рахунку, зазвичай попри всі старання не піднімаються вище середніх досягнень. Понад те, наполегливі спроби «гарненько навантажити» мозок такими заняттями як усний рахунок, шахи наосліп тощо часто можуть призвести до перенапруги і помітному падіння розумової працездатності, пам'яті і самопочуття. З іншого сторони, і обдаровані люди при безладному використанні своїх талантів у такій області як усний рахунок швидко «перегорають» і перестають мати змогу довго й стійко показувати яскраві досягнення. Одне з прикладів вдалого поєднання обох умов (природної обдарованості і великої грамотної роботи з собою) показав уродженець Алтайського краю Юрій Гірський.

Мабуть, єдина науково обгрунтована і докладно розроблена система різкого підвищення швидкості усного рахунки створена була у роки Другої світової цюрихським професором математики Я. Трахтенбергом. Вона відома під назвою «Системи швидкого рахунки». Історія її створення незвична. У 1941 року гітлерівці кинули Трахтенберга до концтабору. Щоб вціліти в нелюдських умовах і зберегти нормальною свою психіку, Трахтенберг почав розробляти принципи прискореного рахунки. За чотири страшних роки у концтаборі професору вдалося створити струнку систему прискореного навчання і дорослих основам швидкого рахунки. По закінченні війни Трахтенберг створив і очолив Цюрихський математичний інститут, який одержав світову популярність.

Також розробкою прийомів швидкого рахунки займалися інші вчені: Яків Исидорович Перельман, Георгій Берман та інші.

 

Робимо висновок, що у всі часи математика була і залишається однією з найцікавіших наук, тому що математичні знання необхідні всім людям. Знати математику – це вміти її застосовувати через створення ситуацій, що стимулюють самостійне відкриття математичних фактів.

 

Не кожен школяр, навчаючись у школі, знає, яку професію він обере в майбутньому, але кожен розуміє, що математика необхідна для вирішення багатьох життєвих завдань: розрахунки в магазині, оплата за комунальні послуги, розрахунок сімейного бюджету і т. д.

 

Актуальність мого дослідження полягає в тому, що в наш час все частіше на допомогу учням приходять калькулятори, і все більша кількість учнів не може обчислювати усно. Адже вивчення математики розвиває логічне мислення, пам’ять, гнучкість розуму, привчає людину до точності, до вміння бачити головне, повідомляє необхідні відомості для розуміння складних завдань, що виникають в різних областях діяльності сучасної людини. Якщо показати, що застосування прийомів швидкого рахунку полегшує обчислення, то можна домогтися того, що підвищиться обчислювальна культура учнів, і їм буде легше вирішувати практичні завдання.

 

Тому в своїй роботі я хочу показати, як можна обчислювати швидко і правильно і що процес виконання дій може бути не тільки корисним, а й цікавим заняттям.

 

  Мета моєї роботи  –  знайти способи усних обчислень для підвищення обчислювальної культури і розвитку інтересу до уроків математики і довести необхідність уміння швидкого рахунку й ефективного використання даних прийомів на практиці.

Відповідно з поставленою метою були визначені завдання:

• Знайти і вивчити матеріал з даної теми «Таємниці усного обчислення»;
• Розглянути і показати на прикладах застосування нестандартних способів при множенні чисел ;
• Допомогти собі і друзям опанувати обчислювальні навички, розвиваючи при цьому пам'ять і увагу.

Гіпотеза дослідження: Існуючі спеціальні способи виконання дій, які  дозволяють звести обчислення до усних, розраховані на розум «звичайної» людини і не потребують унікальних здібностей.

 

 

Таблиця множення на «пальцях»

 

Таблиця множення - ті необхідні у житті кожної людини знання, які слід елементарно завчити, що у перші  шкільні роки дається не просто.

 Це вже потім легко «клацаємо» приклади на множення: 2·3, 3·5, 4·6 тощо. З віком люди , щоправда, дедалі більше забувають як множнити, якщо лічильної практики давно вже не відали. Тому віддаються до влади калькулятора чи сподіваються на свіжість знань друзів. Проте, оволодівши однієї невигадливому технікою «ручного» множення, ми можемо запросто відмовитися від послуг калькулятора. Але відразу уточню, що говорю лише про шкільну таблицю множення, тобто для чисел від 2 до 9, які множать на числа від 1 до 10.

 

  Множення для числа 9 

 9·1, 9·2 ... 9·10 - легше вивітрюється з пам'яті й важче перераховується вручну методом складання, проте саме з числа 9 множення легко відтворюється «пальцями». Розставимо пальці обох рук, повернемо руки долонями вниз. Подумки привласніть пальцях послідовно числа від 1 до 10, починаючи з мізинця лівої руками і закінчуючи мізинцем правої руки (це зображено малюнку).

 

Припустимо, хочемо помножити 9 на 3. Загинаємо палець з номером, рівним числу, на яке ми множили дев'ятку. У прикладі потрібно загнути палець з номером 3. Кількість пальців зліва загнутого пальця показує нам кількість десятків у відповідь, кількість пальців справа - кількість одиниць. Зліва маємо 2 не загнуті пальці, справа - 7 пальців. Отже, 9·3=27. Нижче  на  малюнку детально показаний весь принцип "обчислення".

 

 

 

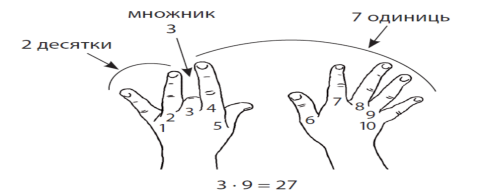
Ще приклад: потрібно обчислити 9·8=?. У процесі скажімо, що на посаді «лічильної машинки» необов'язково можуть виступати пальці рук. Візьміть, приміром, 10 клітинок у зошиті. Закреслимо 8-му клітинку. Зліва залишилося 7 клітинок, справа - 2 клітинки. Отже, 9·8=72. Усе дуже просто.

 

 

Способи швидкого додавання та віднімання натуральних чисел

 

    Якщо один із доданків збільшити на декілька одиниць, то з отриманої суми потрібно відняти стільки ж одиниць.

Приклад.

364+592=364+(592+8)-8=364+600-8=956

 

    Якщо один із доданків збільшити на декілька одиниць,а другий зменшити на стільки ж одиниць,то сума не зміниться.

Приклад.

997+856=(997+3)+(856-3)=1000+853=1853

 

    Якщо від’ємник збільшить на декілька одиниць і зменшуване збільшити на стільки ж одиниць, то різниця не зміниться.

Приклад.

1351-994=(1351+6)-(994+6)=1357-1000=357

 

    Якщо від суми двох чисел відняти різницю тих же чисел, то в результаті отримаємо подвоєне менше число: (а+б)-(а-б)=2б.

Приклад.

(57+23)-(57-23)=46

 

   Якщо до суми двох чисел додати їх різницю, то в результаті отримаємо подвоєне число : (а+в)+ (а-в) = 2а.

Приклад.

(74+26)+(74-26)=148

 

    Додавання в стовпчик. Сума цифр кожного розряду додається окремо. Цифра десятків в сумі попереднього розряду додається з цифрою одиниць наступної суми.

Приклад.

 

 

 

 

 

 

 

 

 

 

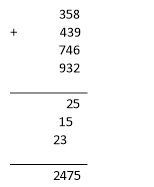
Способи швидкого множення і ділення натуральних чисел

 

Використовуємо закон розподільного множення відносно додавання і віднімання до множників, однин із яких у вигляді суми або різниці.

Приклад.

8∙318=8∙(310+8)=2480+64=2544

7∙196=7∙(200-4)=1400-28=1372

 

    Множення методом Фурроля. Для отримання одиниць перемножують одиниці множників, для отримання десятків множить десятки одного на одиниці другого множника і навпаки, та результати додають, для одержування сотень перемножують десятки. Цей спосіб множення слідує із тотожності:

 ( 10а+в)(10с+d)=100ac+10(ad+вc)+вd

Приклад.

37∙48=1776

А) 8∙7=56 пишемо 6,пам’ятаємо 5;

Б) 8∙3+4∙7+5=57, пишемо ?, пам’ятаємо 5;

В) 4∙3+5=17, пишемо 17.

 

     Методом Фурроля можна перемножити усно двоцифрові числа від 10 до 20.

Приклад.

12∙14=168 множимо так:

А) 2∙4=8

Б) 1∙2+1∙4=6

В) 1∙1=1

 

    Можна помножити і трьохцифрові на двоцифрові.

Приклад. 125∙23=2875

А) 3∙5=15, пишемо 5, пам’ятаємо 1;

Б) (3∙2+2∙5)+1=17, пишемо 7, пам’ятаємо 1;

В) (3∙1+2∙2)+1=8, пишемо 8

Г) 2∙1=2, пишемо 2.

 

 

Множення чисел, у яких число десятків однакове,

а сума одиниць дорівнює 10

   Число десятків любого множника помножить на число, яке більше на 1, потім перемножуємо окремо одиниці цих чисел і на кінець до першого результату справа дописати другий. Цей спосіб базується на тотожності:

(10а+в)∙(10а+с)=100а(а+1)+вс, де в+с=10

 

Приклад

13∙17=221

А) 1∙(1+1)=2

Б) 3∙7=21, пишемо справа 21

204∙206=42024

А) 20∙(20+1)=420, пишемо 420

Б) 6∙4=24, пишемо справа 24

 

Множення чисел на 11

Записати останню цифру числа (цифру із розряду одиниць), потім послідовно справа наліво записали суму сусідніх двох цифр множеного і на кінець першу цифру множеного.

Приклад.

54∙11=594

А)пишемо 4

Б) 4+5=9

В) пишемо 5.

124∙11=1(1+2) (2+4)∙4=1364

 

Якщо одна із сум сусідніх цифр буде більша 9, то відповідному місці записують цифри одиниць одержаної суми, а до наступної суми добавляють 1. Додають одиницю і до наступної цифри множеного, якщо попередня сума перевищувала 9.

Приклад.

58∙11=638

А) пишемо 8

Б) 5+8=13, пишемо 3, пам’ятаємо 1

В) 5+1=6, пишемо 6.

3765∙11=41415

А) пишемо 5

Б) 5+6=11, пишемо 1, пам’ятаємо 1

В) (7+6)+1=14, пишемо 4, пам’ятаємо 1

Г) (3+7)+1=11, пишемо 1, пам’ятаємо 1

Д) (3+1)= 4, пишемо 4.

 

Множення на числа виду аа

Помножимо число спочатку на а, потім на 11.

Приклад.

123∙55=(123∙5)∙11=615∙11=6(6+1)(5+1)∙5=6765

 

 

 

 

Множення двоцифрового числа на 111

  Справа на ліво потрібно записати: Останню цифру першого множника(цифру із розряду одиниць), сума цифр першого множника, знову сума його цифр і на кінець його першу цифру. Якщо сума цифр двоцифрових  чисел більше за 9, тоді записуємо цифру одиниць кожної суми, а до наступного результату додаємо 1.

Приклад.

42∙111=4(4+2) (4+2)∙2=4662

68∙111=7548

А) пишемо останню цифру 8;

Б) 6+8=14, пишемо 4, пам’ятаємо 1.

В) (6+8)+1=15, пишемо 5, пам’ятаємо 1;

Г) 6+1=7, пишемо 7.

 

Множення одноцифрового чи двоцифрового числа на 37

 Спосіб базується на рівностях

2∙37=74, 3∙37=111.

Приклад.

6∙37=37∙3∙2=222

8∙37=(6+2)∙37=222+74=296

45∙37=(48-3)∙37=12∙4∙37-3∙37=16∙3∙37-3∙37=3∙37(16-1)=111∙15=1665.

 

Множення на 5, 25, 125

Поділіть число відповідно на 2,4,8, а результат помножте на 10,100,1000

46∙5=46:2∙10=230

48∙25=48:4∙100=1200

32∙125=32:8∙1000=4000

Якщо  множник не ділиться на 2,4, або 8 то ділення проводимо з остачею. Потім остачу множать відповідно на 10,100,1000, а остачу на 5,25, або 125.

Приклад.

53∙5=26∙10+1∙5=265(53:2=26 і 1 в остачі)

43∙25=10∙100+3+25=1075(43:4=10 і 3 в остачі)

66∙125=8∙1000+2∙125=8250(66:8 і 2 в остачі)

 

Ділення на 5, 25, 125

Помножимо число відповідно на 2, 4, 8 і розділити на 10,100,1000.

Приклад.

220:5=220∙2:10=44

1300:25=1300∙4:100=52

9250:125=9250∙8:1000=74

   Інколи зручно міняти порядок дій, виконуючи спочатку ділення на 10,100, 1000,  а потім множення.

 

Множення на 9, 99, 999

  До першого множника допишуть стільки нулів, скільки дев’яток у другого множника і з результату відняти перший множник.

Приклад.

286∙9=2860-286=2574

23∙99=2300-23=2277

18∙999=18000-18=17982

 

 

Піднесення до квадрату двоцифрових чисел,

що мають 5 десятків

   До 25 додати цифру в розряді одиниць і до результату дописати справа квадрат числа одиниць, так, щоб отримати чотирицифрове число. Цей спосіб особливий на тотожність  = 100∙(25+а)+а²

Приклад.

51²=2601           а) 25+1=26,пишемо 26 

                         б)12=1, дописуємо 01

58²=3364           а) 25+8=33, пишемо 33   

                         б) 82=64, дописуємо 64 

 

 

Піднесення чисел до квадрату що закінчується на 5

    Для того, щоб піднести число до квадрату, потрібно помножити кількість десятків цього числа на таке саме число плюс одиниця і дописати до утвореного числа 25.

Приклад.     

    75²=5625

а)7∙ (7+1)=56;

б) дописати до утвореного числа 25, отримали 5625.   

  Так само можна  підносити до квадрату  і трицифрові числа, які закінчуються п'ятіркою.

Наприклад, 135 на 135. Спочатку множимо 13 (десятків) на 14, потім до результату дописуємо 25. Отримаємо 18225.  13 на 14 легко можна помножити, скориставшись цікавим способом, який я вам пропоную далі.

 

 

Множення двозначного числа на 101

Мабуть, найпростіше правило: припишіть ваше число перед самим собою. Множення закінчено.

Приклад:

57 ∙ 101= 5757

42 ∙ 101= 4242

Систематизовані правила множення

 

•              Множення на 5:   Помножте на 10 і розділіть на 2.
•              Множення на 6:   Іноді простіше помножити на 3, а потім на 2.
•              Множення на 9:   Помножте на 10 і відніміть вихідне число.
•              Множення на 12: Помножте на 10 і двічі додайте вихідне число.
•              Множення на 13: Помножте на 3 і 10 разів додайте вихідне число.
•              Множення на 14: Помножте на 7, а потім - на 2.
•              Множення на 15: Помножте на 10 і 5 разів додайте вихідне число, як у   попередньому прикладі.
•              Множення на 16: Якщо хочете, 4 рази помножте на 2. Або помножити на    8, а потім на 2.
•              Множення на 17: Помножте на 7 і 10 разів додайте вихідне число.
•              Множення на 18: Помножте на 20 і двічі відніміть вихідне число.
•              Множення на 19: Помножте на 20 і відніміть вихідне число.
•              Множення на 24: Помножте на 8, а потім на 3.
•              Множення на 27: Помножте на 30 і 3 рази відніміть вихідне число.
•              Множення на 45: Помножте на 50 і 5 разів відніміть вихідне число.
•              Множення на 90: Помножте на 9 і припишіть 0.
•              Множення на 98: Помножте на 100 і двічі відніміть вихідне число.
•              Множення на 99: Помножте на 100 і відніміть вихідне число.

Множення великих чисел

Якщо вам потрібно перемножити великі числа усно і одне з них парне, то ви можете скористатися методом спрощення множників, зменшивши парне число в два рази, а другий збільшуючи в два рази:

32∙125 це 16∙250 це 8 ∙ 500 це 4 ∙ 1000 = 4000

 

Множення  двоцифрових чисел, близьких до 100

   Нехай нам потрібно 93 помножити на 95. Традиційно такі приклади учні  виконують у стовпчик. Оригінальність даного обчислення можна розкрити таким ходом виконання:

1.              доповнити кожен множник до 100, це буде відповідно 7 (100 – 93) і 5 (100 – 95);
2.                     віднімемо від першого множника доповнення другого (93 – 5 = = 88) або від другого множника доповнення першого (95 – 7 = 88). І в першому, і в другому випадках одержимо 88 – це перші цифри шуканого добутку – сотні.
3.                     Перемножимо доповнення (7∙5)=35 – це останні дві цифри шуканого добутку. Отже, 93∙95=8835 .

Дроби

1. Множення цілого числа на змішане.

Множення цілого числа на змішане число може бути виконано за правилом множення числа на суму, так як змішане число є сума цілого числа і дроби. Пояснимо це на числовому прикладі:

1) .

Але при множенні цілого числа на змішане число можна звернути змішане число в неправильне дріб, потім помножити ціле число на чисельник дробу неправильної, отриманий добуток зробити чисельником шуканого дробу, знаменник ж дробу залишити знаменник множника:

.
 

Як бачимо, перший спосіб простіше і дає можливість швидше виробляти множення.

2) .
 

Перевага першого способу над другим у даному прикладі очевидно. Але можуть бути випадки, коли простіше і швидше можна вирішити приклад другим способом:

3) .
 

Таким чином, при множенні цілого числа на змішане число треба уважно розглянути приклад і застосувати той спосіб, який в даному випадку швидше веде до мети.

 
2. Розподіл змішаного числа на ціле.

Змішане число можна розглядати як суму двох чисел. Отже, поділ змішаного числа на ціле є розподіл суми двох чисел на число. Щоб розділити суму чисел на число, достатньо розділити на це число кожне з доданків, і скласти отримані результати.

Ми знаємо, що всі основні закони арифметичних дій, встановлені для натуральних чисел, зберігають свою силу і для дробових чисел:
1) 348 : 4 = (348 + ): 4 = 348: 4 + : 4 = 87 + = 87 .

Як бачимо, цей спосіб набагато легше (він дає можливість швидше робити обчислення), ніж звичайний спосіб розподілу змішаного числа на ціле з утворенням змішаного числа в неправильну дріб.

2) 252 : 12 = (252 + ): 12 = 252: 12 + : 12 = 21 + = 21 .
 

3. Множення і ділення цілого числа на дріб, яка відрізняється від одиниці на одну частку:

а) множення

1) ;

2) ;

б) поділ

3) .

Розглянемо приклад поділу цілого числа на дріб, причому дріб відрізняється від одиниці на дві і більше часток:

1) .

Як ми бачимо, даний спосіб дає можливість швидше множити і ділити ціле число на дріб, ніж звичайний спосіб, а тому слід розібраний спосіб використовувати при множенні або розподілі цілого числа на дріб.

 

Відсотки

Усне знаходження відсотків числа і числа за даними його відсоткам

Усне знаходження 5%, 25%, 12,5% числа і т.п., а також числа за даними його відсоткам засноване на множенні і діленні на дробу 0,05; 0,25; 0,125 і т.п.
а) Знаходження відсотка від числа.
1) Знайти 25% від 468.

Але можна замінити 25% і звичайної дробом. Цей приклад обчислимо так: .
2) Знайти 12,5% від 728.

Можна 12,5% замінити звичайної дробом: .
 

б) Знаходження числа за даними його відсоткам.
Знайти число, якщо 5% його рівні 492.
 

Як бачимо, спосіб заміни відсотків звичайної дробом іноді дає можливість швидше робити обчислення, ніж множенням на десяткову дріб.

 

Знаходження квадратів числа

1. Таблиця квадратів цілих чисел від 1 до 25 включно.
 

На підставі того, що суми послідовних непарних чисел:
1 + 3 = 4; 1 + 3 + 5 = 9; 1 + 3 + 5 + 7 = 16 і т.д. - представляють собою ряд квадратів, розроблені наступні способи складання таблиці квадратів.

а) Перший спосіб складання таблиці квадратів чисел від 1 до 25.

 

Числа		Квадрати чисел
цілі	непарні
1	1	1
2	3	4
3	5	9
4	7	16
5	9	25
6	11	36
7	13	49
8	15	64
9	17	81
10	19	100
11	21	121
12	23	144
13	25	169
14	27	196
15	29	225
16	31	256
17	33	289
18	35	324
19	37	361
20	39	400
21	41	441
22	43	484
23	45	529
24	47	576
25	49	625

 

У першій колонці написано ряд послідовних цілих чисел, починаючи з одиниці. У другій колонці написано ряд непарних чисел, починаючи з 1. Третя колонка містить ряд квадратів цілих чисел, зазначених у першій колонці.

Таблиця складається так: у першому рядку пишуть число 1; цей перший квадрат додають до непарному числу наступній рядки з другої колонки і отримують другий квадрат 4. Додаючи 4 до третього непарному числу (5) з другої колонки, отримуємо 3 ^2, тобто 9. Взагалі, квадрат числа є сума непарного числа, яке стоїть в одній з ним рядку і безпосередньо передує квадрата. В одній і тій же рядку зліва направо розташовані: 1) ціле число; 2) непарне число, для якого це ціле число є номером у ряді непарних чисел; 3) квадрат цілого числа.

б) Другий спосіб складання таблиці квадратів чисел від 1 до 25.
У першій вертикальної колонці пишуться по порядку цілі числа, починаючи з одиниці. У другій колонці пишеться ряд непарних чисел, починаючи з 3. У третій колонці, яка повинна містити ряд, квадратів всіх цілих чисел, пишеться спочатку квадрат 1, тобто одиниця. Щоб отримати кожний з наступних квадратів, додають до останнього числа третьої колонки то непарне число, яке стоїть зліва від нього, у другій колонці. Кожне з чисел третьої колонки є квадрат відповідного числа першої колонки.

 

Числа		Квадрати чисел
цілі	непарні
1	3	1
2	5	4
3	7	9
4	9	16
5	11	25
6	13	36
7	15	49
8	17	64
9	19	81
10	21	100
11	23	121
12	25	144
13	27	169
14	29	196
15	31	225
16	33	256
17	35	289
18	37	324
19	39	361
20	41	400
21	43	441
22	45	484
23	47	529
24	49	576
25	51	625

 

Числа	Квадрати чисел
1	1
2	4
3	9
4	16
5	25
6	36
7	49
8	64
9	81
10	100
11	121
12	144
13	169
14	196
15	225
16	256
17	289
18	324
19	361
20	400
21	441
22	484
23	529
24	576
25	625

 

в) Третій спосіб складання таблиці квадратів чисел.

Квадрати чисел від 1 до 10 включно визначаємо за таблицею множення: у першій колонці пишемо числа, в другій - їх квадрати. Щоб отримати квадрат наступного числа, до квадрату даного числа додаємо суму даного числа і наступного числа. Розглянемо на числових прикладах.

1) квадрат числа 11 дорівнює 100 + (10 + 11) = 121;

2) квадрат числа 12 дорівнює 121 + (11 + 12) = 144 і т.д.

Пояснення цього способу знаходження квадрата числа наступне:
(K + 1) ² = k ² + ² k • 1 + 1 ² = k ² + [k + (k + 1)].

3) 75 ² = 5625. 76 ² = (75 +1) ² = 75 ² + [75 + (75 + 1)] = 75 ² +
+ (75 + 76) = 5625 + 151 = 5776.

Отримуємо 76 ² = 5776.

 

 

2. Зведення в квадрат і множення з допомогою формул скороченого множення.
 

а) Обчислення за формулою .
.
 

б) Обчислення за формулою .
.
 

в) Особливо корисним виявляється застосування в усних обчисленнях формули .
1) .
2) .

3). 93∙87=( 90+3)(90-3)=8100-9=8091       

4). 66∙54=( 60+6)(60-6)=3600-36=3564

 

Множення

1. Заміна кількох співмножників їх добутком (сполучний  закон множення). 
   1) 17∙25∙4=17∙(25∙4)=17∙100=1700

Щоб перемножити кілька чисел, досить окремі співмножники поєднати в групи, зробити множення по групам, а потім перемножити одержані добутки. 
2)  . 

2. Перестановка співмножників (переставний і сполучний закони множення). 
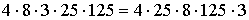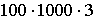    =  =300000. 
   Щоб перемножити кілька чисел, можна поміняти місцями окремі співмножники, з'єднати їх у групи, потім провести множення в групах і перемножити одержані добутки. 
3. Множення добутку на число. 

 =  = =  . 
Щоб помножити добуток декількох чисел на будь-яке число, достатньо один із співмножників помножити на це число і отриманий добуток послідовно помножити на інші співмножники. 

4.  Множення числа на добуток. 

1)  =  =168000. 
Щоб помножити число на добуток декількох чисел, досить помножити це число на перший співмножник, отриманий добуток - на другий, потім новий добуток - на третій і т.д. до кінця. 

До вказаного способу близький прийом множення за допомогою заміни множника відповідним добутком (іноді це називають послідовним множенням). 
2)  . 
5.   Множення добутку на добуток. 
 =  =  =

==  . 
Тут застосовано таке правило: щоб помножити твір декількох чисел на інший твір, досить послідовно перемножити всі співмножники обох творів. 

 

Множення, додавання і віднімання

1. Розподільний закон множення по відношенню до додавання (множення суми чисел на число). 

 . 
Щоб помножити суму декількох чисел на дане число, досить помножити кожний доданок на це число і одержані добутки скласти. 
До вказаного способу з обгрунтування прийому близький спосіб винесення за дужки загального множника або множимо. 
1)  ; 
2)  .

2. Розподільний закон множення по відношенню до вирахуванню     (множення різниці чисел на число).

1.  . 
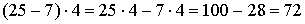   Щоб помножити різницю чисел на яке-небудь число, досить помножити на це число окремо зменшуване і від'ємник і з першого твору відняти друге.
2.  . 
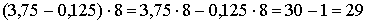   До вказаного способу з обгрунтування прийому близький спосіб винесення за дужки загального множника. 

3. Множення суми на суму. 

=  . 

Щоб помножити суму декількох чисел на іншу суму, можна кожне складова першої суми помножити на кожний доданок друге суми і одержані добутки скласти. 

 

 

 

 

 

 

Математика для всіх

 

Математика – наука не тільки для вчених. Вона потрібна всім. Коли ви йдете в магазин, робите ремонт або слухаєте щоденний прогноз погоди, математика вам може стати в нагоді. Багато хто вважає, що математика – нудна, відірвана від повсякденного життя наука. Може ви теж так думаєте? Давайте подивимося, наскільки простою і захоплюючою може бути математика.

 

Математика в магазині

 

Уявіть, що ви прийшли в магазин і бачите, що там великий розпродаж товарів за зниженими цінами. Річ, спочатку коштувала 35 грн, знижена в ціні на 25 відсотків. Схоже, що це досить хороша знижка. Скільки ж ця річ коштує тепер? На допомогу приходить арифметика. Спочатку відніміть відсоток знижки від 100. Вийде 75 відсотків (100 відсотків – 25 відсотків = 75 відсотків). Потім помножте отриманий результат (в даному випадку 75 відсотків, або 0,75) на початкову вартість. Нова ціна складе 26,25 грн (35 × 0,75 = 26,25). Тепер, коли ви знаєте ціну речі після знижки, можна вирішити, чи вигідною буде покупка. А якщо у вас немає з собою калькулятора? Можна зробити підрахунки в розумі.

 

Наприклад, якась річ, спочатку коштувала 45 грн, зменшується на 15 відсотків. Ось підказка, як це можна порахувати в голові. Для порівняння візьмемо 10 відсотків. Щоб порахувати, скільки складе 10 відсотків від будь-якого числа, потрібно поділити це число на 10. Це відносно легко зробити в умі. Потім, знаючи, що 15 = 10 + 5, а 5 – це рівно половина від 10, можна швидко вирахувати остаточний результат за допомогою додавання і віднімання. Давайте спробуємо це зробити. Якщо 10 відсотків від 45 буде 4,5, значить 5 відсотків від 45 буде в два рази менше, тобто 2,25. А 15 відсотків – це сума двох цих чисел, в нашому випадку це 6,75 (4,50 + 2,25 = 6,75). Після цього від 45 відніміть 6,75 і вийде нова ціна – 38,25 грн. До речі, ви можете скористатися подібним методом, підраховуючи торговий податок на якусь річ або те, скільки чайових потрібно додати до рахунку в ресторані. Звичайно, в цих випадках потрібно не віднімати, а додавати результат до первісної вартості.

 

Проте будьте обережні і не помиліться, вважаючи в розумі. Якщо плаття або штани, знижені в ціні на 40 відсотків, потім ще раз були знижені в ціні на 40 відсотків, це означає, що річ була знижена в ціні лише на 64 відсотки, а не на 80. Друга уцінка вираховується від уже зниженої ціни, а не від початкової. Можливо, покупка все одно буде вигідною, але все-таки добре знати, що скільки коштує. Однак є завдання, які за допомогою однієї арифметики не вирішити.

Арифметика (ця назва походить від грецького слова, що означає «число») вважається найдавнішим розділом математики. Арифметика виникла тисячоліття тому і була відома ще в стародавньому Вавілоні, Китаї та Єгипті. За допомогою арифметики ми кожен день можемо робити елементарні підрахунки і вимірювати будь-що в оточуючому нас матеріальному світі.

 

Ремонт у квартирі

 

 Припустимо, ви хочете перестелити підлогу у своїй квартирі, а кошти у вас обмежені. Перш ніж піти в магазин, сядьте і подумайте, що вам потрібно для ремонту. Найбільше питання: скільки матеріалу вам буде потрібно? Тут вам знадобляться основи геометрії. Матеріал для підлоги в магазинах часто обчислюється в квадратних одиницях. Наприклад, у ділянки підлоги в один квадратний метр обидві сторони – довжина і ширина – дорівнюють одному метру. Перш ніж порахувати, скільки матеріалу вам буде потрібно, спочатку визначте, яка площа підлоги в кожній з кімнат і в коридорі вашої квартири.

 

На планах більшості будівель підлога представлена квадратами і прямокутниками. Тому наступна формула допоможе вам зробити підрахунки: пл. = дов. × шир. (Площа – це довжина, помножена на ширину). За цією геометричною формулою можна порахувати площу прямокутника або квадрата. Щоб проілюструвати, як користуватися цією формулою, уявімо, що вам потрібно перестелити підлогу у всіх кімнатах, окрім кухні та ванної.

 

Виміряйте кожну кімнату і намалюйте план. Квадрати і прямокутники на цьому плані будуть показувати розміри і розташування кімнат. Використовуючи вищезгадану формулу, спробуйте порахувати, скільки квадратних метрів матеріалу для підлоги вам буде потрібно. Ось ще підказка: можна обчислити площу кожної кімнати окремо, а результати скласти. Або, можливо, швидше порахувати площу всієї квартири і відняти з неї площу кухні та ванної кімнати.

 

Слово «геометрія» прийшло з грецької мови і буквально означає «вимір землі». Геометрія пов’язана з обчисленням площі, довжини, об’єму і інших параметрів тіл, фігур і ліній. Для розрахунку всіляких параметрів фігур і тіл є зручні формули. Щодня вчені, інженери і дизайнери користуються цими формулами, щоб робити точні обчислення. Але математика не обмежується лише арифметикою і геометрією.

 

 

 

Математика на кожен день

 

 Алгебра і математичний аналіз – теж розділи математики. Протягом століть математика була і залишається воістину універсальною мовою всіх людей, незалежно від статі, віросповідання та культури. У науці, промисловості, бізнесі і в повсякденному житті математика здатна допомогти нам вирішити найскладніші питання. Чи намагаєтеся ви розкрити таємниці Всесвіту або ж плануєте сімейний бюджет, мова цифр допоможе вам досягти успіху.

 

Навіть якщо ви не любите математику в школі, чому б зараз не глянути на неї по-новому? Математика – це свого роду мова, а вчити будь-яку мову краще за все на практиці. Спробуйте кожен день вдаватися до математики у своєму житті: наприклад, вирішуйте головоломки або грайте в математичні ігри. Можливо, у вас все чудово вийде і ваше ставлення до математики зміниться.

 

А якщо хочете потренуватись усно обчислювати, пограйте з товаришем (з татом, сестричкою...) в гру  «Дивовижні перетворення телефонного номера». Перший гравець називає номер телефона (наприклад шестизначний) і першим розставляє між його цифрами знаки дій та дужок, другий (третій. четвертий. кількість гравців не має значення) усно знаходять значення утвореного числового виразу , використовуючи прийоми усних обчислень,– хто швидше. Наступний вираз складає гравець, котрий справився найшвидше із попереднім виразом. Із цифр даного номера можна скласти безіч різних числових виразів таких, які можна обчислити, використовуючи прийоми швидкого обчислення.  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Висновки

 

Як бачимо, швидка лічба це не є таємниця під сімома печатками, а науково розроблена система. Якщо є система, її можна вивчати й опанувати. Усі розглянуті мною методи усного множення говорять про багаторічний  інтерес  не тільки вчених, а й найпростіших людей до гри з цифрами.

 

У наше століття високих технологій і використання комп'ютера вміння швидко та усно обчислювати досить складні приклади в жодному разі не втратило своєї актуальності. Гнучкість розуму дає підстави пишатися людям, а здатність, наприклад, швидко усно обчислювати викликає відвертий подив.  Такі навички допоможуть фахівцям в царині навчанні, у побуті, у професіональній діяльності. З іншого боку, швидка лічба - справжня гімнастика для розуму, яка дозволяє у найскладніших життєвих ситуаціях знаходити у найкоротший термін хороші й нетрадиційні рішення.

 

Впевнена, що мною розглянута невелика частина відомих у світі математичних методів і прийомів обчислень, які можна назвати не тільки цікавими, а й корисними. Знання прийомів швидкого рахунку дозволяє спрощувати обчислення, економити час, розвиває логічне мислення і гнучкість розуму.

 

Вважаю, що моя гіпотеза частково підтвердилася. Дійсно, деякі прийоми можна вважати спрощеними. Але частина з них - просто цікаві, нестандартні, які розвивають    увагу, пам'ять.                Користуйтесь власною головою - це швидше, надійніше, і дешевше!  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список літератури

 

Берман Р. М. Прийоми рахунки, вид. 6-те, М., Физматгиз, 1959. Кордемский Б. А. Ахадов А. А. Дивовижний світ чисел: Книга учнів, – М. Освіта, 1986р.

Нагібін Ф. Ф., Канін Є. С. Математична шкатулка: Посібник для учнів 4-8 кл. середовищ. шк. – 5-е вид. – М. Освіта, 1988.

Мінських Е. М. «Від гри до знань», М. «Просвещение», 1982р.

Борзенко В. І. Горєлов А. Г. Вимоги до дослідницьких робіт з математики / / Журнал «Дослідницька робота школярів», 2005. № 3.с.63-64

Черемних Г. В. Художнє оформлення результатів дослідної роботи / / Журнал «Дослідницька робота школярів», 2005. № 3.с.65-82

 Бантова М. А. Система формування обчислювальних навичок. //Нач. шк - 1993.-№ 11.-с. 38-43.

Белошистая А. У. Прийом формування усних обчислювальних умінь не більше 100 // Початкова школа. - 2001.- № 7

Берман Р. М. Прийоми рахунку, вид. 6-те, М.: Физматгиз, 1959.

 Боротьбенко Є І. Контроль навичок... усних обчислень. //Нач. шк. - 1972. - № 7.- з. 32-34.

Вроблевский. Як навчиться легко і швидко вважати. - М.-1932.-132с. Гольдштейн Д. М. Техніка швидких обчислень. М.: Учпедгиз, 1948.

 Гончар Д. Р. Устний рахунок і пам'ять: загадки, прийоми розвитку, ігри // У сб. Устный рахунок і пам'ять. Донецк:Сталкер, 1997 р. Катлер Еге.

 Мак-Шейн Р. Система швидкого рахунку по Трахтенбергу. - М.: Учпедгиз.- 1967. ?150с.

 Мартель Ф. Прийоми швидкого рахунку. - Пб. ?1913. ?34с.

Мартинов І. І. Устний рахунок школяреві, що гами для музиканта. // Початкова школа. - 2003. - № 10. - З. 59-61.

 Мелентьев П. У. «Швидкі і усні обчислення.» М.: «Гостехиздат», 1930. Перельман Я. І. Швидкий рахунок. Л.: Союздрук, 1945

Пекеліс У. Д. «Твої можливості, людина!» М.: «Знання», 1973. Робер Токэ «2 + 2 = 4» (1957) (англомовне видання: «Магія чисел» (1960))

 Сорокін А. З. Техніка рахунку. М.: «Знання», 1976.

 Сухорукова А. Ф. Більше уваги усним обчисленням. //Нач. шк. - 1975.-№ 10.-с. 59-62.

 Фаддейчева Т. І. Навчання усним обчисленням // Початкова школа. - 2003. - № 10.

 Фаермарк Д. З. «Завдання настало з початком картини.» М.: «Наука». Шаригін І.Ф. Шевкин А.В. Математика. Завдання на кмітливість. 2000 р.