Презентація "Тригонометричні функції"
Про матеріал
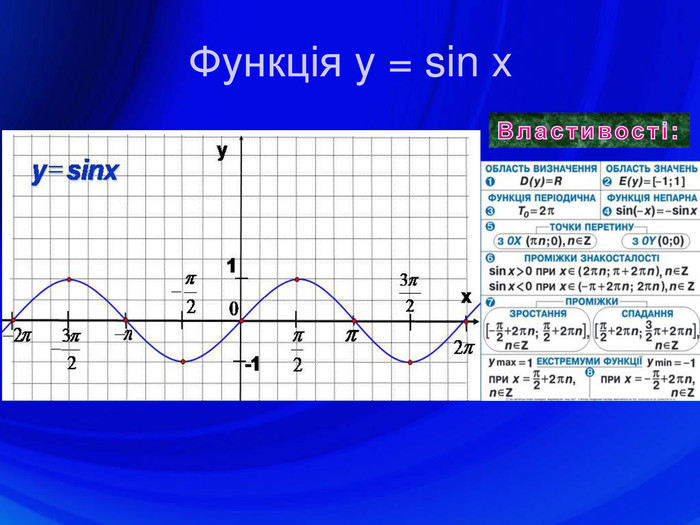
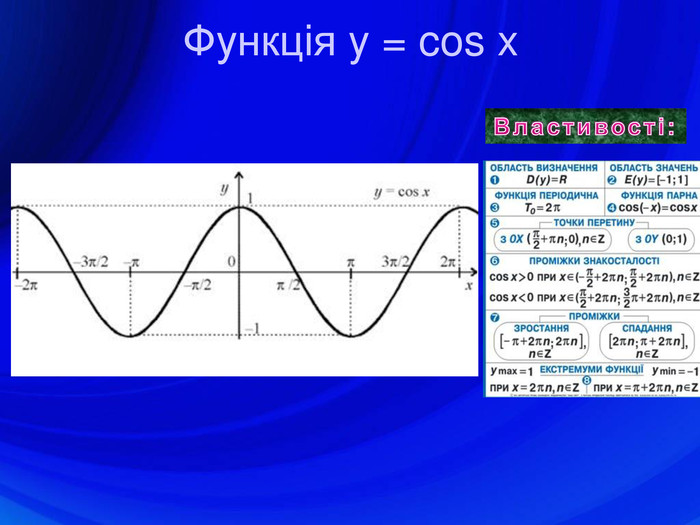
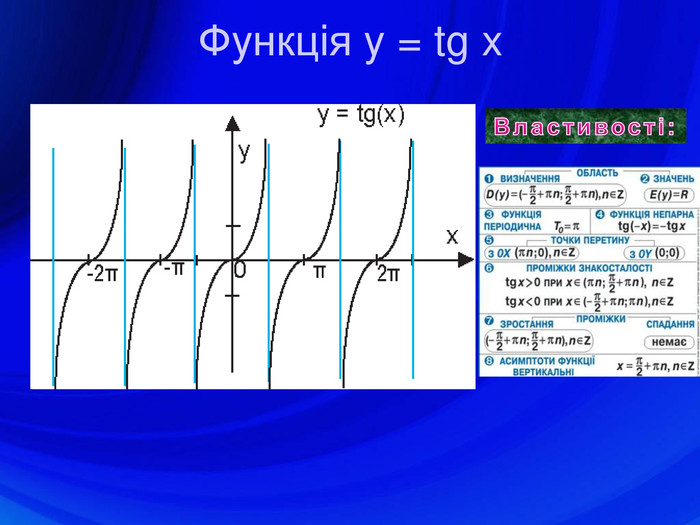
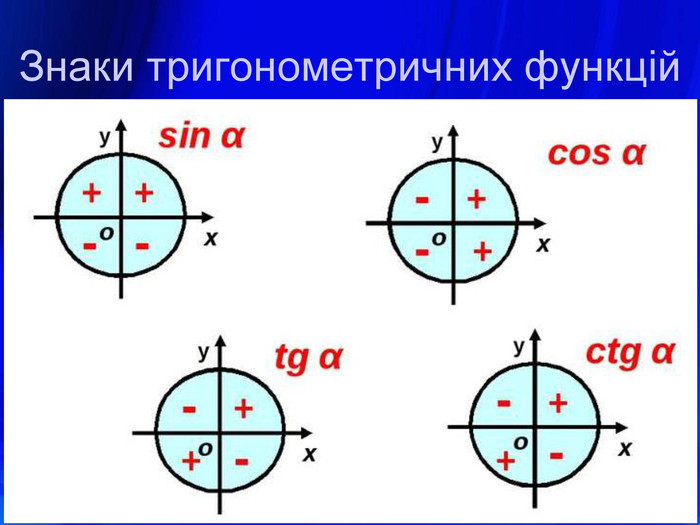
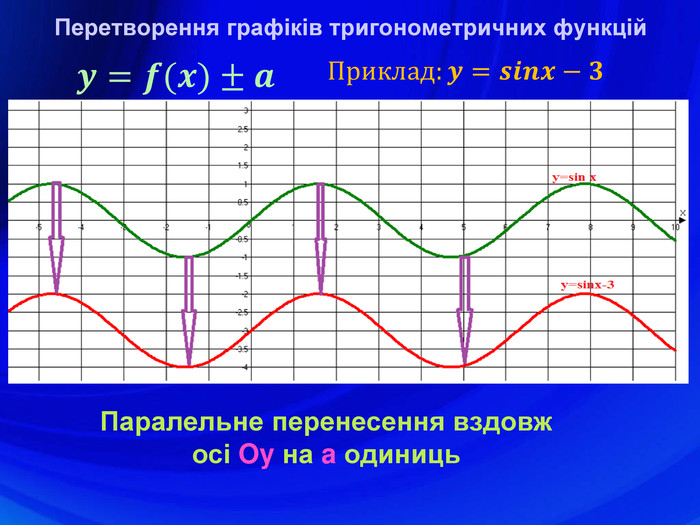
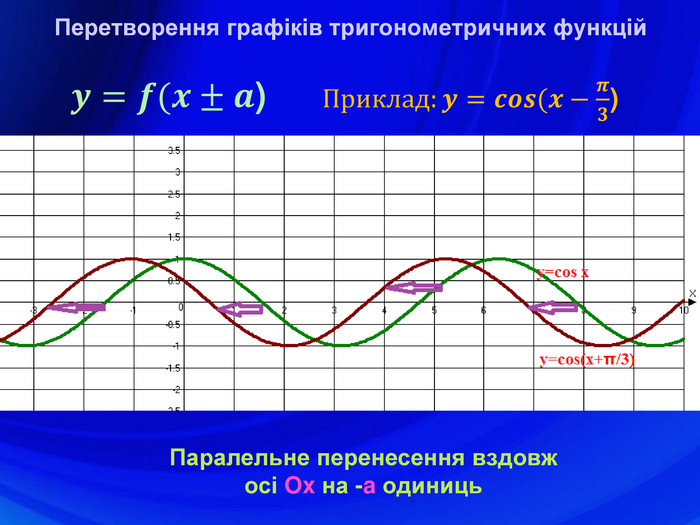
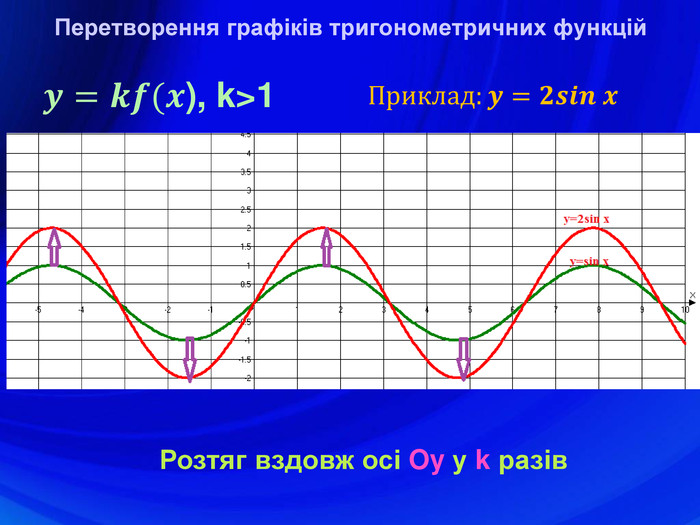
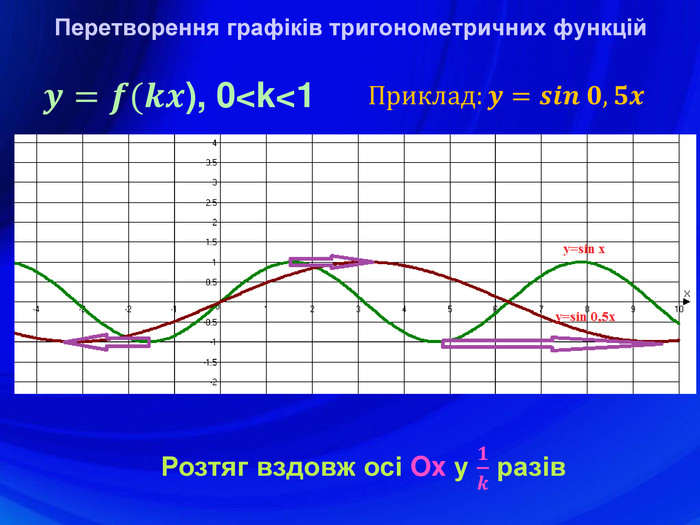
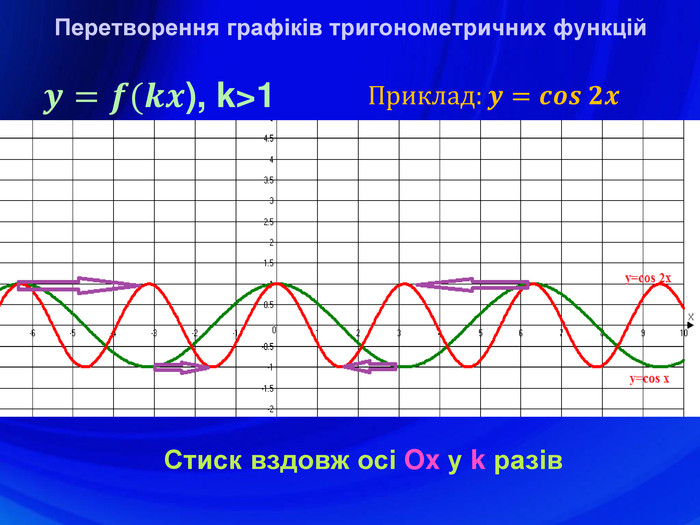
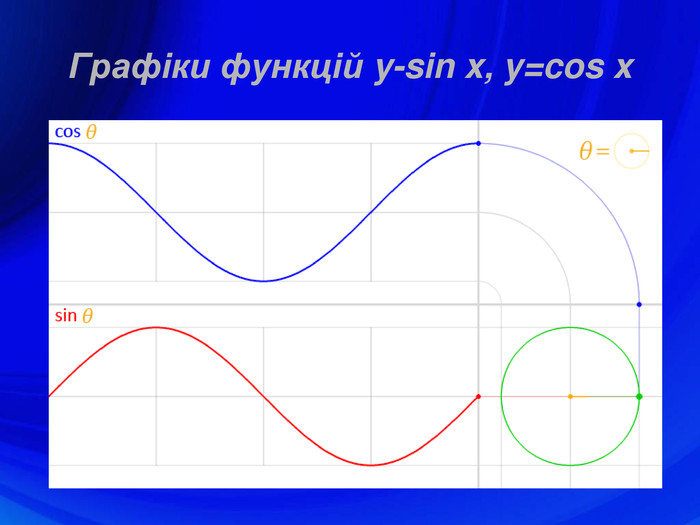
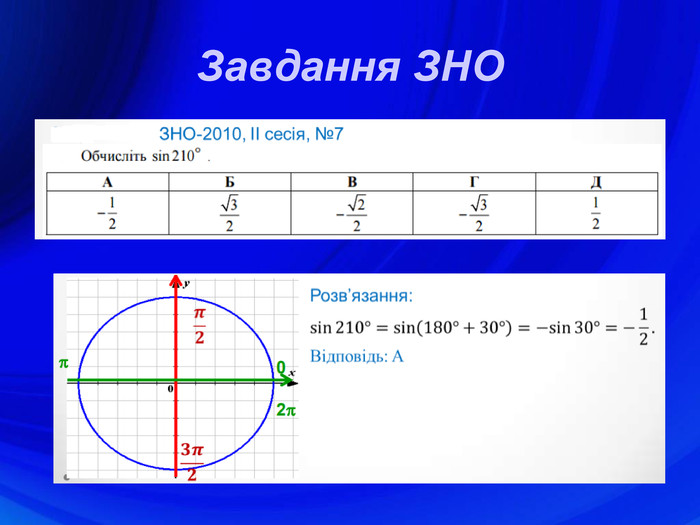
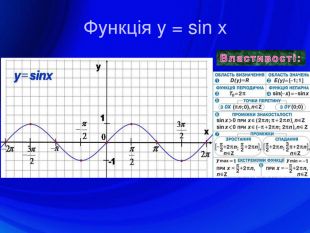
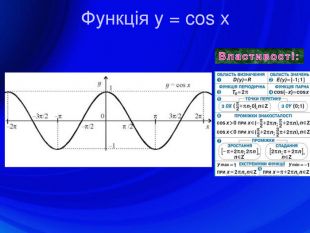
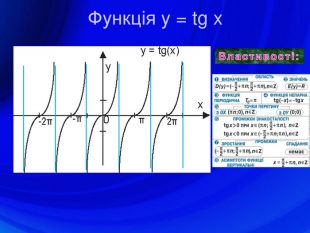
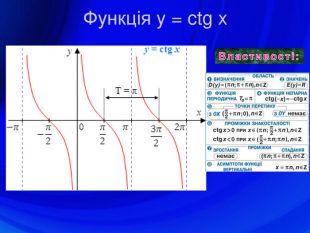
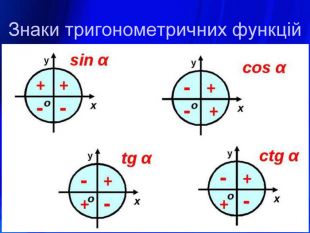
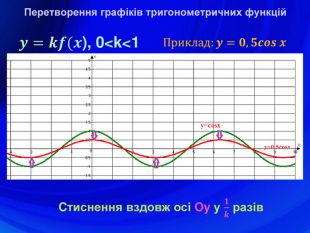
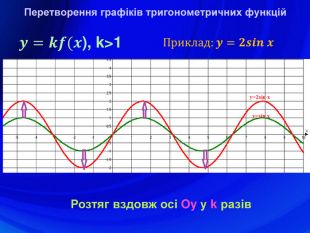
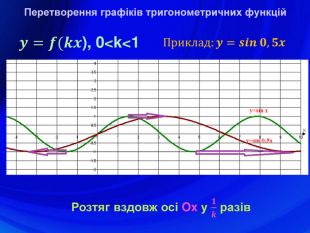
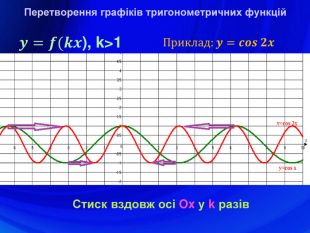
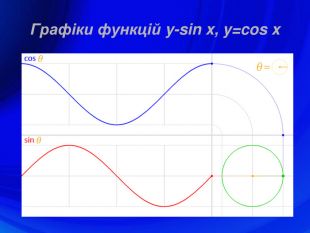
У презентації подано означення тригонометричних функцій, їх властивості, графіки, формули зведення, перетворення графіків тригонометричних функцій, а також завдання ЗНО з цієї теми. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку