Посібник для уроків алгебри ІІ семестр 8 класу
Шановні восьмикласники!
Ви продовжуєте вивчати алгебру. А сприяти вам буде навчальний посібник, який ви тримаєте в руках.
Посібник складається з двох тем. Кожна тема має таку структуру:
- перший урок – урок розбору блоку навчальної інформації;
- наступні уроки – уроки фронтального опрацювання матеріалу, на яких проводиться робота з засвоєння понять, термінів і правил блоку навчальної інформації, також наведені вправи і завдання для відпрацювання практичних умінь і навичок.
-
між уроками фронтального опрацювання ви будете виконувати завдання індивідуального опрацювання матеріалу, вправи якого не наведені в даному посібнику. Але він містить завдання для підготовки до індивідуального опрацювання, позначені

- в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен покаже свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.
Також в кінці посібника є повторення всього матеріалу, який ми вивчали протягом року.
Нехай Бог посилає вам мудрості у вивченні алгебри!!!
Тема №4. Квадратні корені. Дійсні числа
Урок №1

Квадратні корені. Дійсні числа
Завдання математики не навчання лічби, а
навчання прийомів людського мислення під час лічби
Л. М. Толстой
Питання
-
Функція
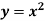 , її графік та властивості.
, її графік та властивості.
- Квадратний корінь.
- Дійсні числа.
-
Функція
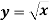 , її графік та властивості.
, її графік та властивості.
Література
Істер О.С. Алгебра: підручник для 8-го класу загальноосвітніх навчальних закладів, К.: Ґенеза, 2016 рік, § 13 – 19, стор. 112 – 169.
|
||||||||||||||
|
1.1 |
Графіком функції |
|
||||||||||||
|
1.2 |
Властивості функції
|
|||||||||||||
|
1.3 |
Графічний спосіб розв’язування рівнянь f(x) = g(x)
|
Відповідь: |
||||||||||||
|
||||||||||||||
|
2.4 |
Квадратним коренем з невід’ємного числа а називається таке число х, квадрат якого дорівнює а. |
16: 4 і – 4; 121: 11 і – 11. |
||||||||||||
|
2.5 |
Арифметичним квадратним коренем з невід’ємного числа а називається таке невід’ємне число х, квадрат якого дорівнює а.
|
|
||||||||||||
|
2.6 |
Властивості арифметичного квадратного кореня:
|
=
|
||||||||||||
|
2.7 |
Розв’язування рівнянь виду
|
|
||||||||||||
|
2.8 |
Розв’язування рівнянь виду
|
|
||||||||||||
|
||||||||||||||
|
3.9 |
Числа, які використовуються при лічбі називаються натуральними. Множина натуральних чисел позначається – N. |
1, 2, 6, 12, 132 |
||||||||||||
|
3.10 |
Натуральні числа, протилежні їм числа і число 0 складають множину цілих чисел Z. |
1, 45, – 8, – 148 |
||||||||||||
|
3.11 |
Число, яке можна подати у вигляді дробу Множина раціональних чисел позначається – Q. |
|
||||||||||||
|
3.12 |
Кожне раціональне число можна подати у вигляді скінченного, або нескінченного періодичного десяткового дробу. |
|
||||||||||||
|
3.13 |
Нескінченні неперіодичні десяткові дроби складають множину ірраціональних чисел. |
|
||||||||||||
|
3.14 |
Множину всіх раціональних та ірраціональних чисел називають множиною дійсних чисел R. |
|
||||||||||||
|
||||||||||||||
|
4.15 |
Властивості функції
|
|
||||||||||||
Урок №2
«Одного разу ви зрозумієте, що ваша
велич починається там, де закінчується гординя»
Збірка «Хліб наш насущний»
Фронтальне опрацювання матеріалу
Функція ![]() , її властивості та графік. Графічний спосіб розв’язування рівнянь
, її властивості та графік. Графічний спосіб розв’язування рівнянь
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.3 блоку № 4.
- Дай відповідь на питання, запропоновані вчителем у презентації.
- На електронну пошту нашої школи прийшов лист від Лінійної функції та Прямої пропорційності. Але він захищений паролем. Потрібно усно виконати вправи, щоб його розгадати.
-
Після введення паролю, ми можемо прочитати лист і допомогти нашим функціям. Для цього розглянемо побудову графіка функції
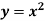 .
.
- Щоб краще вивчити цю функцію, необхідно пройти протокол вивчення.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Письмово розв’яжи вправи, стор.116 підручника: 506; 508.
Завдання 3.
Розглянь приклад розв’язування вправи


Завдання 4.
Використовуючи розглянутий приклад, письмово розв’яжи вправи:
-
На рисунку зображено графіки функцій
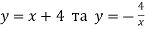 . Розв’яжіть рівняння
. Розв’яжіть рівняння 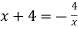 .
.
- Розв’яжіть графічно рівняння:
-
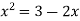 ;
;
-
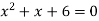 ;
;
-
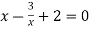 .
.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 5.
Задача «Маркетинг»
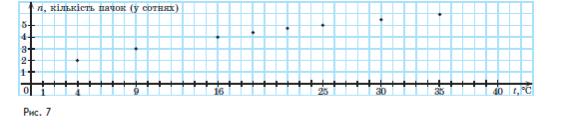
 Кондитерська компанія реалізує новий вид шоколадних цукерок. Щоб покращити збут нової продукції, компанія замовила на телеканалі трансляцію рекламного ролика протягом чотирьох місяців (вересень – грудень). Відомо, що у вересні трансляція ролика тривала 10 с, а кожного наступного місяця збільшувалась.
Кондитерська компанія реалізує новий вид шоколадних цукерок. Щоб покращити збут нової продукції, компанія замовила на телеканалі трансляцію рекламного ролика протягом чотирьох місяців (вересень – грудень). Відомо, що у вересні трансляція ролика тривала 10 с, а кожного наступного місяця збільшувалась.
Відділ маркетингу, дослідивши обсяги продажу цукерок за цей час, отримав результати подані на рисунку. Кожна з чотирьох точок із координатами ![]() відповідає одному місяцю;
відповідає одному місяцю; ![]() – тривалість ролика щодня (у с);
– тривалість ролика щодня (у с); ![]() – кількість проданих цукерок (у тис. шт.), проданих протягом місяця.
– кількість проданих цукерок (у тис. шт.), проданих протягом місяця.
Користуючись рисунком, дайте відповідь на запитання:
- Скільки шоколадних цукерок було продано у вересні?
- Скільки секунд тривав щоденний рекламний ролик у жовтні?
-
Якою формулою можна задати залежність змінною
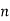 від змінної
від змінної 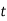 ?
?
-
Припустимо, що залежність змінної
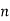 від
від 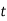 збережеться і в майбутньому. Скільки тисяч цукерок буде продано в січні, якщо протягом цього місяця щоденний рекламний ролик триватиме 50 с?
збережеться і в майбутньому. Скільки тисяч цукерок буде продано в січні, якщо протягом цього місяця щоденний рекламний ролик триватиме 50 с?
Урок №3
«Нейтральним бути не можна»
Андрій Кузьменко
Фронтальне опрацювання матеріалу
Квадратний корінь. Арифметичний квадратний корінь. Рівняння ![]() та
та ![]()
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.5, 2.7, 2.8 блоку № 4.
- Усно дай відповіді на питання:
-
Що є графіком функції
 ?
?
-
Сформулюй властивості функції
 .
.
- Сформулюй алгоритм графічного способу розв’язування рівнянь.
-
Що називають квадратним коренем з невід’ємного числа
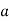 ?
?
-
Що називають арифметичним квадратним коренем з невід’ємного числа
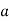 ?
?
-
Як розв’язують рівняння виду
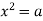 ?
?
-
Як розв’язують рівняння виду
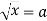 ?
?
Завдання 2.
-
При яких умовах є правильною рівність
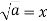 ?
?
- Усно розв’яжи вправи, стор. 120 підручника: 523; 524; 526.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконай вправи, стор. 121 – 122 підручника: 530 (1, 3, 5, 7); 534 (2, 4, 6, 8); 536 (1, 3); 539.
Завдання 4.
- Розв’яжіть рівняння:
-
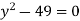 ;
;
-
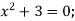
-
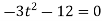 ;
;
-
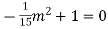 .
.
- Знайдіть значення виразу:
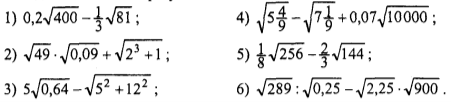
- Обчислити:

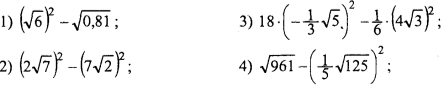
- Самостійно, за допомогою мобільних телефонів, виконати інтерактивну вправу, зашифровану у QR-коді:
Урок №4
«Глядіть, щоб ніхто
нікому не віддавав злом за зло, але завжди
дбайте про добро один для одного й для всіх!»
1послання ап. Павла до солунян 5:15
Фронтальне опрацювання матеріалу
Раціональні, ірраціональні, дійсні числа. Числові множини
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.5, 2.7, 2.8, 3.9 – 3.14 блоку № 4.
- Усно дай відповіді на питання:
-
Що є графіком функції
 ?
?
-
Сформулюй властивості функції
 .
.
- Сформулюй алгоритм графічного способу розв’язування рівнянь.
-
Що називають квадратним коренем з невід’ємного числа
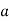 ?
?
-
Що називають арифметичним квадратним коренем з невід’ємного числа
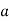 ?
?
-
Як розв’язують рівняння виду
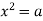 ?
?
-
Як розв’язують рівняння виду
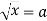 ?
?
- Які числа називаються натуральними?
- Які числа називаються цілими?
- Які числа називаються раціональними?
- Які числа називаються ірраціональними?
- Які числа називаються дійсними?
 Завдання 2.
Завдання 2.
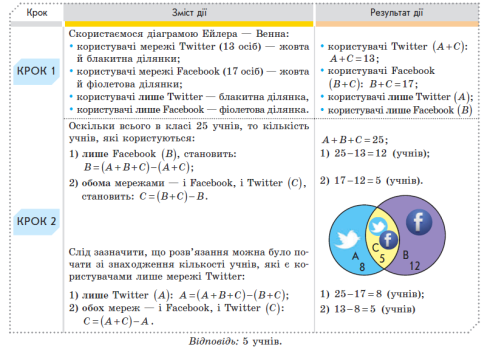
Розгляньте приклад розв’язування вправи:
У класі 25 учнів. Серед них 13 учнів користуються соціальною мережею Twitter, а 17 учнів — мережею Facebook. Визначте, скільки учнів класу є користувачами обох соціальних мереж.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
- Відомо, що 18 працівників фірми тримають собак, 16 – котів, причому 2 працівники тримають і собаку, і кота. Скільки всього співробітників працює на фірмі, якщо всі вони мають домашніх тварин?
- На фестиваль приїхала група учнів з 15 дітей. Із них 8 дітей взяти участь у фотоконкурсі, 9 – конкурсі з пісочної анімації. Скільки дітей взяли участь в обох конкурсах?
Завдання 4.
-
Визначте, яким множинам (
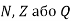 ) належать числа:
) належать числа:
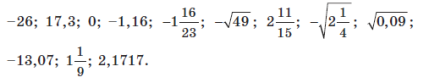
- Усі учні класу прочитали або книжку про Дон Кіхота, або про Шерлока Холмса. Причому про Дон Кіхота читали 85% учнів класу, а про Шерлока Холмса – 75%. Визначте, скільки відсотків учнів прочитали книгу і про Дон Кіхота, і про Шерлока Холмса.
- Подайте числа у вигляді нескінченного періодичного десяткового дробу
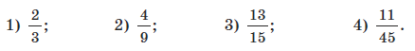
- Розташуйте числа у порядку спадання:
![]()
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 5.
Задача «Києво-Могилянська академія»
Національний університет «Києво-Могилянська академія» налічує 6 факультетів: інформатики, правничих наук, економічних наук, гуманітарних наук, соціальних наук та
соціальних технологій, природничих наук. Студентська колегія університету складається із 6 студентів (по одному представнику від кожного факультету).
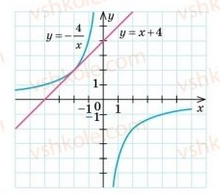
На рисунку подано діаграми (А–Д), на яких зображено відношення між множинами A і B.

- Виберіть діаграму, на якій елементами множини A є студенти студентської колегії, а елементами множини B – студенти факультету економічних наук.
- Виберіть діаграму, на якій елементами множини A є студенти університету, а елементами множини B – студенти факультету економічних наук.
- Виберіть діаграму, на якій елементами множини A є студенти факультету правничих наук, а елементами множини B – студенти факультету економічних наук.
- У чергових виборах до студентської колегії представника від факультету економічних наук взяли участь 135 студентів. Кожний студент голосував за одного з чотирьох кандидатів. Переміг той кандидат, який набрав найбільше голосів (строго більше, ніж кожний із трьох інших). Яку найменшу кількість голосів міг набрати переможець?
Урок №5
«Мудрий бачить лихе – і
ховається, а безумні йдуть – і караються»
Книга приповістей Соломонових 27:12
Фронтальне опрацювання матеріалу
Властивості арифметичного квадратного кореня
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.14 блоку № 4.
- Усно дай відповіді на питання:
-
Що є графіком функції
 ?
?
-
Сформулюй властивості функції
 .
.
- Сформулюй алгоритм графічного способу розв’язування рівнянь.
-
Що називають квадратним коренем з невід’ємного числа
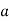 ?
?
-
Що називають арифметичним квадратним коренем з невід’ємного числа
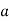 ?
?
-
Як розв’язують рівняння виду
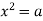 ?
?
-
Як розв’язують рівняння виду
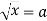 ?
?
- Які числа називають натуральними? Цілими? Раціональними? Ірраціональними? Дійсними?
- Сформулювати властивості арифметичного квадратного кореня.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
- Розглянь приклад 1, 2, 3, 4, стор. 138 – 139 підручника.
- Користуючись розглянутими прикладами, письмово виконай вправи, стор. 141 – 143 підручника: 615 (1, 3, 5); 617 (1, 3, 5); 625 (2, 4, 6); 627 (2, 4, 6); 633 (1, 3); 635 (1, 3, 5).
Завдання 3.
- Розглянь приклади 5, 6, 7, стор. 139 – 140 підручника.
- Користуючись розглянутими прикладами, письмово виконай вправи, стор. 142 – 143 підручника: 629 (1, 3, 5); 638; 642 (1, 3, 5).
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 4.
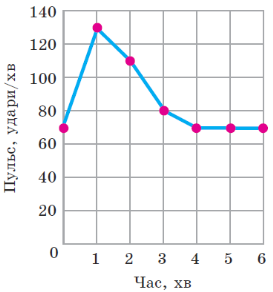
Задача «Тренажерний зал»
Олег щодня відвідує тренажерний зал. Одного разу він вирішив виміряти частоту пульсу перед початком фізичних вправ – вона становила 70 ударів за хвилину. Після виконання вправ протягом хвилини Олег знову виміряв пульс, а потім повторив вимірювання ще кілька разів – через кожну хвилину, без додаткових фізичних навантажень. Удома Олег побудував діаграму, що відображає отримані результати (див. малюнок).
П’ятеро друзів Олега, побачивши ці результати, зробили такі висновки.
- Після виконання фізичних вправ частота пульсу збільшилася на 50 ударів за хвилину.
- Для зниження частоти пульсу знадобилося менше часу, ніж для її зростання.
- Через 4 хв після початку вимірювання частота пульсу становила 80 ударів за хвилину.
- Частота пульсу прийшла до норми менш ніж за 6 хв.
- після виконання фізичних вправ частота пульсу зросла вдвічі.
З якими висновками можна погодитися?
Уроки №6, 7
«Хліб з неправди солодкий людині,
та піском потім будуть наповнені її уста»
Книга приповістей Соломонових, 20:17
Фронтальне опрацювання матеріалу
Тотожні перетворення виразів, що містять квадратні корені
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитай тези 2.4. – 3.14 блоку № 4.
- Усно встав пропущені слова у визначення і правила:
-
Квадратним коренем з … числа
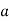 називається …
називається …
- Арифметичним квадратним коренем з … числа називається таке …
- Числа, які …. називаються натуральними.
- Число, яке можна подати у вигляді дробу, називається …
- Нескінченні … дроби складають множину … чисел.
- Допиши рівності:
-
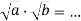 ; 4)
; 4) 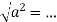 ;
;
-
 5)
5) 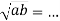 ;
;
-
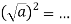 ; 6)
; 6) 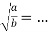
Завдання 2.
- Уважно прочитай § 18, стор. 147 – 150 підручника.
- Усно дай відповідь на запитання:
- як виконувати дії з виразами, що містять однакові підкореневі вирази;
-
як звільнитися від ірраціональності в знаменнику або в чисельнику дробу.
- Виконати кросворд:
Питання кросворду:
1. Як називають невід’ємний квадратний корінь із невід’ємного числа? (Арифметичний). Сформулюйте означення арифметичного квадратного кореня.
2. Як називають знак арифметичного квадратного кореня? (Радикал)
3. Назвіть відомого французького математика, який ввів сучасне позначення радикала? (Декарт)
4. Як одним словом назвати додатні числа і нуль? (Невід’ємні)
5. Із якого числа неможливо добути квадратний корінь? (Від’ємного)
6. Числа, які можна подати у вигляді нескінченного десяткового періодичного дробу. (Раціональні)
7. Числа, які не можна подати у вигляді нескінченного десяткового періодичного дробу, але можна подати у вигляді нескінченного неперіодичного десяткового дробу. (Ірраціональні)
8. Назвіть знак, який необхідно поставити при порівнянні чисел ![]() і
і ![]() . (Більше)
. (Більше)
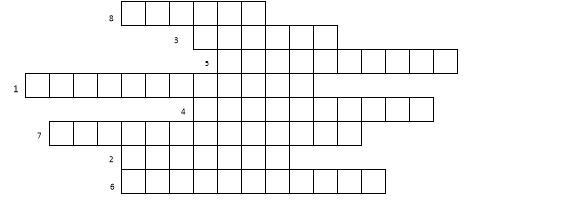
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконай вправи, стор. 151 – 154 підручника:
- 661 (1, 3, 5); 663; 665 (1, 3, 5, 7); 667; 671 (2, 4, 6).
- 677; 683; 686; 688.
Урок №8
«Будьте терпимими один
до одного, прощайте одне одного…»
Послання ап. Павла до колосян 3:13
Фронтальне опрацювання матеріалу
Функція ![]() , її графік та властивості
, її графік та властивості
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитай тези 2.4 – 4.15 блоку № 4.
- Усно встав пропущені слова у визначення і правила:
-
Квадратним коренем з … числа
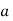 називається …
називається …
- Арифметичним квадратним коренем з … числа називається таке …
- Числа, які …. називаються натуральними.
- Число, яке можна подати у вигляді дробу, називається …
- Нескінченні … дроби складають множину … чисел.
- Допиши рівності:
-
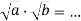 ; 4)
; 4) 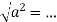 ;
;
-
 5)
5) 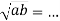 ;
;
-
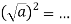 ; 6)
; 6) 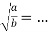
-
Область визначення функції
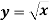 …
…
- Область значень – …
-
Якщо
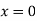 , то
, то 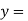 …
…
- Графік функції …
-
При збільшенні
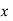 збільшуються …
збільшуються …
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
- Розглянь приклад:

- Користуючись розглянутим прикладом, виконай вправу:

Завдання 3.
Письмово виконай вправи:
-
Не виконуючи побудови графіка функції
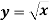 , вкажіть, через які з даних точок проходить цей графік: А(0,16; 0,4), В(–64;8), С(30,25; 5,5).
, вкажіть, через які з даних точок проходить цей графік: А(0,16; 0,4), В(–64;8), С(30,25; 5,5).
-
Не виконуючи побудови, знайдіть координати точки перетину графіка функції
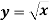 та прямої 1)
та прямої 1) 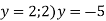 .
.
-
Розв’яжіть графічно рівняння: 1)
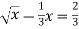 ; 2)
; 2) 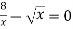
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
 Завдання 4.
Завдання 4.
Письмово виконай вправу:



 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
- Письмово виконай вправи:
- Обчисли:
1) ![]() ;
;
2) ![]() .
.
-
Винеси множник з-під знака кореня: 1)
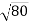 ; 2)
; 2) 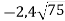 .
.
-
Спрости вираз:
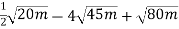 .
.
-
Розташуй в порядку зростання числа:
 ..
..
-
Скороти дріб: 1)
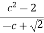 ; 2)
; 2) 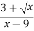 .
.
-
Розв’яжи графічним способом рівняння:
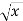 =
= 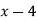 .
.
Урок №10
«Хто любить навчання, той любить
пізнання, а хто докір ненавидить, той нерозумний»
Книга приповістей Соломонових 12 :1
Внутрішньопредметне узагальнення матеріалу
Квадратні корені. Дійсні числа
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 4.
- Дай письмово відповідь на питання, запропоновані вчителем.
Завдання 2.
Усно виконай вправи:
-
Яка з точок належить графіку функції
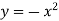 ?
?
|
А |
Б |
В |
Г |
|
(2; 4) |
(3; 6) |
(1; 2) |
(3; – 9) |
- Яке з тверджень правильне?
|
А |
Б |
В |
Г |
|
Множина цілих чисел є частиною множини натуральних чисел |
0,4545…= 0,(45) |
|
|
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
-
Обчисли значення виразу: 1)
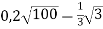 ; 2)
; 2) 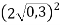 .
.
-
Спрости вираз:
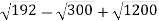 .
.
-
Звільнись від ірраціональності у знаменнику дробу: 1)
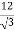 ; 2)
; 2) 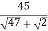 .
.
-
Скороти дріб:
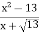 .
.
-
Спрости вираз:
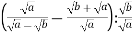 .
.
Урок №12
Міжпредметне узагальнення матеріалу
Перетворення виразів, що містять квадратні корені
Формування компетентностей:
- Предметна компетентність: узагальнити та систематизувати знання учнів з теми «Квадратні корені»; удосконалити вміння виконувати перетворення виразів, що містять квадратні корені;
- Ключові компетентності:
- Спілкування державною мовою – грамотно висловлюватися рідною мовою, доречно і коректно вживати в мовленні математичну термінологію;
- Уміння вчитися впродовж життя – відбирати й застосовувати потрібні знання та способи діяльності для досягнення навчальної мети;
- Соціальна та громадянська компетентності – співпрацювати в команді, виділяти та виконувати власну роль у командній роботі;
- Інформаційна компетентність – вільне користування комп’ютерною технікою, виконання он-лайн вправ на LearningApps;
- Загальнокультурна компетентність - орієнтуватися у досягненнях національної культури
Обладнання та наочність: ноутбуки 4+1 (підключені до мережі Інтернет), математичне доміно «Вирази із квадратними коренями»; капелюх.
Хід уроку
- Організаційний етап. Емоційне налаштування.
Вправа «Капелюшок» - учні в колі під музику передають один одному капелюшок та одягають собі на голову. На кому музика зупиняється, той відповідає на запитання вчителя (добути квадратний корінь з числа).
Розподіл учнів на 4 групи.
- Усні вправи для розвитку обчислювальних навичок.
- Завдання на Google-карті «пропонують» визначні міста України. За розповіддю вчителя назвати місто, показати його на карті та виконати запропоноване завдання:
https://drive.google.com/open?id=1XFX69pWM7EBbaAc1f-i_3D3L9jP8LTy-&usp=sharing
-
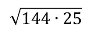 Київ
Київ
Колиска української історії, зосередження величних пам’яток архітектури, мальовничих місць і куточків відпочинку найвищого рівня. Михайлівський золотоверхий собор, комплекс Софія Київська та Києво-Печерська лавра – це лише мала частина того, чим захоплюватися у цьому місті. - Львів
![]() Колоритне місто з багатою історією. Напевно, кожен, хто побував у ньому, пам’ятає п’янкий аромат кави і шоколаду на мощених вуличках. Старовинні будиночки, цікаві музеї, верхівки церков – все це можна побачити у цьому місті.
Колоритне місто з багатою історією. Напевно, кожен, хто побував у ньому, пам’ятає п’янкий аромат кави і шоколаду на мощених вуличках. Старовинні будиночки, цікаві музеї, верхівки церков – все це можна побачити у цьому місті.
- Одеса
![]() Самобутнє місто, в якому можна вічно відкривати щось нове і незвичайне. Це місто унікальне тим, що побачити пам’ятки тут можна на кожному кроці. Придбайте квиток в театр опери та балету, прогуляйтеся по затишних мощених вуличках і мальовничих набережних, відвідайте морські ресторанчики , відомі пам’ятники архітектури. А ще це місто пов’язують із гумором.
Самобутнє місто, в якому можна вічно відкривати щось нове і незвичайне. Це місто унікальне тим, що побачити пам’ятки тут можна на кожному кроці. Придбайте квиток в театр опери та балету, прогуляйтеся по затишних мощених вуличках і мальовничих набережних, відвідайте морські ресторанчики , відомі пам’ятники архітектури. А ще це місто пов’язують із гумором.
-
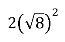
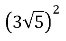 Вінниця
Вінниця
Друга назва цього міста – місто-фонтан. Це не дивно, адже фонтанчики розташовані по всьому місту. Одним з найвідоміших фонтанів у місті є світломузичний фонтан Рошен. - Кам’янець-Подільський
![]() З усіх куточків світу з’їжджаються сюди туристи для того, щоб подивитися на знамениту фортецю. Ця фортеця прекрасно збереглася до наших днів і не перестає вражати своєю монументальністю і величчю. Саме завдяки цій фортеці місто називають “музеєм під відкритим небом”.
З усіх куточків світу з’їжджаються сюди туристи для того, щоб подивитися на знамениту фортецю. Ця фортеця прекрасно збереглася до наших днів і не перестає вражати своєю монументальністю і величчю. Саме завдяки цій фортеці місто називають “музеєм під відкритим небом”.
- Запоріжжя
![]() Це місто з унікальним минулим, колиска українського козацтва. У центральній частині міста розташований найбільший острів на Дніпрі – Хортиця, де для відвідувачів відкрито історико-культурний центр “Запорізька Січ”.
Це місто з унікальним минулим, колиска українського козацтва. У центральній частині міста розташований найбільший острів на Дніпрі – Хортиця, де для відвідувачів відкрито історико-культурний центр “Запорізька Січ”.
-
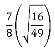 Луцьк
Луцьк
Це місто дуже часто називають містом-фортецею, хоча, незважаючи на свою багату історію, він залишається молодим і блискучим містом. У ньому можна відвідати старовинні церкви і монастирі, замки епохи Середньовіччя і чудові собори. -
Харків
Місто з унікальною історією, зосередження освіти і культури, місце з особливою енергетикою і ритмом. Найвідоміші пам’ятки міста - це чудовий Успенський собор і Покровський монастир. А ще це місто певний час було столицею України.
- Математичне доміно «Вирази із квадратними коренями» - робота в групах.
|
СТАРТ
|
|
|
4
|
|
|
3
|
|
|
6
|
|
|
10
|
|
|
36
|
|
|
5
|
|
|
28
|
|
|
14
|
|
|
21
|
ФІНІШ |
- Робота в групах «Подорож по країні Квадракорїї» (робота за ноутбуками)
Завдання групам: пройти запропонованим маршрутом на карті та виконати он-лайн вправи у LearningApps ( групи заздалегідь зареєстровані на LearningApps під певним логіном)
Карта подорожі:
Результат виконання вправ учитель та учні спостерігають на вчительському ноутбукові в режимі «Статистика»
1). Вправа «Пазли»
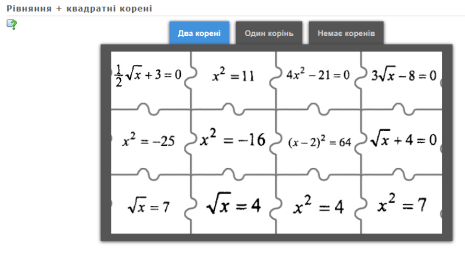
2). Вправа «Знайди пару» (додаткове завдання)

3). Вправа «Відповідності сітки»

4). Вправа «Перегони»

Учитель спостерігає за роботою учнів в групах. З-за необхідності надає допомогу у виконанні вправ.
- Оцінювання роботи учнів (на підставі самооцінки та спостережень учителя за роботою учнів протягом уроку)
Тема №5. Квадратні рівняння
Урок №1

Квадратні рівняння
«Любіть своїх ворогів, добро робіть тим,
хто ненавидить вас. Благословляйте тих, хто вас
проклинає, і моліться за тих, хто кривду вам чинить»
Євангеліє від Луки 6:27, 28
Питання
- Квадратні рівняння.
- Квадратний тричлен.
- Рівняння, які зводяться до квадратних.
- Рівняння як математичні моделі прикладних задач.
Література
Істер О.С. Алгебра: підручник для 8-го класу загальноосвітніх навчальних закладів, К.: Ґенеза, 2016 рік, § 20 – 26, стор. 170 – 221.
|
1.Квадратні рівняння |
|||
|
1.1 |
Рівняння виду |
|
|
|
1.2 |
Квадратне рівняння, в якому хоча б один із коефіцієнтів b або c дорівнює 0, називають неповним квадратним рівнянням. |
|
|
|
1.3 |
Розв’язування неповних квадратних рівнянь |
|
|
|
1)
Відповідь: |
Відповідь: |
||
|
2)
|
|
||
|
3) |
|
||
|
1.4 |
Формула коренів квадратного рівняння
D – дискримінант (розрізнювач)
|
|
|
|
1.5 |
Якщо
Якщо D = 0, то рівняння має один корінь
Якщо
|
||
|
1.6 |
|
|
|
|
1.7 |
Квадратне рівняння, у якому а = 1 називається зведеним. |
|
|
|
1.8 |
Теорема Вієта
Сума коренів зведеного квадратного рівняння
|
||
|
1.9 |
Теорема, обернена до теореми Вієта
Якщо числа |
||
|
2. Квадратний тричлен |
|||
|
2.10 |
Квадратним тричленом називається многочлен виду |
|
|
|
2.11 |
Коренем квадратного тричлена називається значення змінної, при якому значення цього тричлена дорівнює 0. |
||
|
2.12 |
Формула розкладання квадратного тричлена на лінійні множники Теорема.
Якщо |
||
|
3. Рівняння, які зводяться до квадратних |
|||
|
3.13 |
Рівняння виду |
||
|
3.14 |
Біквадратні рівняння розв’язують методом введення нової змінної, позначивши |
||
|
3.15 |
Способи розв’язування рівнянь, які зводяться до квадратних:
|
||
|
4. Рівняння як математичні моделі прикладних задач |
|||
|
4.16 |
|
||
Урок №2
«Господь моє світло й спасіння моє, кого буду боятись?
Господь то твердиня мого життя, кого буду лякатись?»
Псалом 27:1
Фронтальне опрацювання матеріалу
Означення квадратного рівняння. Неповні квадратні рівняння
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитай тези 1.1 – 1.3 блоку № 5.
- Усно дай відповіді на запитання:
- Що називають квадратним рівнянням?
- Що таке неповне квадратне рівняння?
- Як розв’язати неповне квадратне рівняння?
- Скільки коренів може мати квадратне рівняння?
- Як називають коефіцієнти квадратного рівняння?
Завдання 2
Виконай усно вправи, стор. 173: 775, 776.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3
Письмово виконати завдання:
- Виписати коефіцієнти квадратного рівняння:
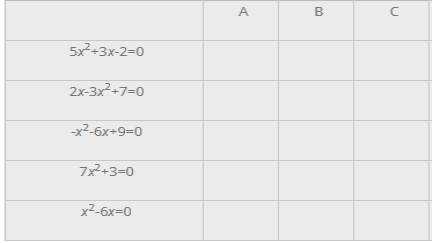
- Склади квадратне рівняння, у якого:
- старший коефіцієнт дорівнює 5, другий коефіцієнт дорівнює 6, а вільний член дорівнює 1;
-
старший коефіцієнт дорівнює
 , другий коефіцієнт дорівнює 0, а вільний член дорівнює – 9.
, другий коефіцієнт дорівнює 0, а вільний член дорівнює – 9.
- Виконай письмово вправи, стор. 174 – 175 підручника: 784 (2, 4, 6); 787 (1, 3, 5), 793 (1, 3).
-
При якому значенні
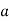 число 3 є коренем рівняння
число 3 є коренем рівняння 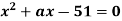 ?
?
- Розв'яжіть рівняння:
-
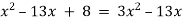 ;
;
-
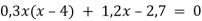 .
.
- Знайдіть корені рівняння:
-
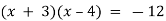 ;
;
-
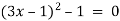 ;
;
-
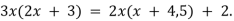
Уроки №3, 4
"Свого тягаря поклади ти на Господа, і тебе Він
підтримає, Він ніколи не дасть захитатися праведному!"
Псалом 55:23
Фронтальне опрацювання матеріалу
Формула коренів квадратного рівняння
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.6 блоку № 5.
- Усно дай відповіді на запитання:
- Що називають квадратним рівнянням?
- Що таке неповне квадратне рівняння?
- Як розв’язати неповне квадратне рівняння?
- Скільки коренів може мати квадратне рівняння?
- Як називають коефіцієнти квадратного рівняння?
- Від чого залежить кількість коренів квадратного рівняння?
- Як записується формула для обчислення дискримінанта?
- Як записується формула коренів квадратного рівняння? Спрощена формула?
Завдання 2
Виконай усно вправи:
- Яке з рівнянь є квадратним?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Вкажи коефіцієнти
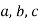 у квадратному рівнянні
у квадратному рівнянні 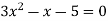 .
.
|
А |
Б |
В |
Г |
|
1; 2; 3 |
3; – 1; – 5 |
1; – 2; 3 |
1; 2; – 3 |
-
Розв’яжи рівняння
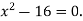
|
А |
Б |
В |
Г |
|
2 |
– 4 і 4 |
– 2 |
4 |
- Скільки різних коренів має квадратне рівняння, якщо: 1) D = 7; 2) D = – 7; 3) D = 5; 4) D = 0.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3
- Розглянь приклад розв’язування квадратного рівняння.

- Знайди дискримінант і визнач кількість коренів квадратного рівняння:

- Розв’яжи рівняння:
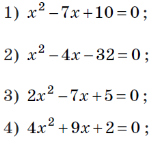
-
Зведи до вигляду
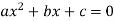 та розв’яжи рівняння:
та розв’яжи рівняння:
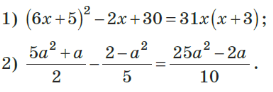
Завдання 4.
Виконай письмово вправи, стор. 181 підручника:
1 варіант: 818 (1); 820 (2); 2 варіант: 818 (2); 820 (1).
Завдання 5.
- Розв’яжи рівняння:

- Розв’яжи рівняння:
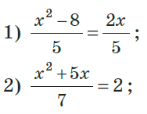
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 6.
Виконай письмово вправи:
-
Розв’яжи рівняння:
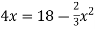 .
.
-
Розв’яжи рівняння:
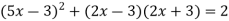 .
.
-
При якому значенні а обидва корені рівняння
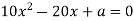 рівні між собою?
рівні між собою?
-
При якому значенні k рівняння
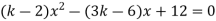 має один корінь?
має один корінь?
- Стор. 182 підручника: 824 (1).
Уроки №5, 6
«Бо Господь дає мудрість, з Його уст знання й розум»
Книга приповістей Соломонових 2:6
Фронтальне опрацювання матеріалу
Теорема Вієта
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.9 блоку № 5.
- Усно дай відповіді на запитання:
- Які рівняння називаються квадратними?
- Що таке неповне квадратне рівняння?
- Яке квадратне рівняння називається зведеним?
- Як розв’язати неповне квадратне рівняння?
- Від чого залежить кількість коренів квадратного рівняння?
- Як записується формула для обчислення дискримінанта?
- Як записується формула коренів квадратного рівняння? Спрощена формула?
- Сформулюй теорему Вієта.
- Сформулюй теорему, обернену до теореми Вієта.
Завдання 2.
Усно розв’яжи вправи:
- Яке з рівнянь є зведеним квадратним рівнянням?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Яке з чисел є добутком коренів рівняння
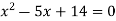 ?
?
|
А |
Б |
В |
Г |
|
5 |
14 |
– 5 |
– 14 |
- У якого з рівнянь сума його коренів дорівнює – 8?
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
- Переглянь історичну довідку «Франсуа Вієт та його теорема» (презентація).
- Розглянь приклад виконання вправи.

- Користуючись розглянутим прикладом, виконай завдання 4.
Завдання 4.
Письмово розв’яжи вправи:
- Знайди «підбором» корені рівняння:
|
1) х2 – 6х + 8=0 |
2) х2 –2х –15=0 |
3) х2 –15х + 36=0 |
|
4) х2 + 5х – 6=0 |
5) х2 + 7х– 8=0 |
6) х2 –10х – 39=0 |
- Один із коренів квадратного рівняння дорівнює –2. Знайди другий корінь рівняння: 1) х2 + 17х + 30 = 0; 2) х2 – 6х – 16 = 0.
- Склади квадратне рівняння, корені якого дорівнюють: 1) 5 і 4 ; 2) 12 і – 8 ; 3) – 2 і 8 ; 4) – 8 і 8 ; 5) 5 і 13 ; 6) – 2,5 і 2.
- Склади таблицю відповідностей між квадратним рівнянням та його коренями:
А) х2 – 4х + 3 = 0; 1) 2 і 5;
Б) х2 – 24х – 81 = 0; 2) – 4 і 3;
В) х2 + 8х + 12 = 0; 3) – 3 і 27;
Г) х2 + х – 12 = 0; 4) – 6 і - 2;
Д) х2 – 7х + 10 = 0. 5) 1 і 3.
|
|
1 |
2 |
3 |
4 |
5 |
|
А |
|
|
|
|
|
|
Б |
|
|
|
|
|
|
В |
|
|
|
|
|
|
Г |
|
|
|
|
|
|
Д |
|
|
|
|
|
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 5.
Письмово виконай вправи, стор. 188 підручника: 840 (1, 3, 5); 845; 847; 849 (1, 3, 5).
Завдання 6.


Завдання 7. (домашнє)
Виконати завдання на картках швидкого рахунку, запропоновані вчителем.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
Розв’яжи рівняння: 1)
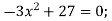 2)
2) 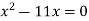 .
.
-
Скільки коренів має рівняння
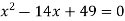 ?
?
-
Знайди методом підбору корені рівняння:
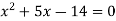 .
.
-
Розв’яжи рівняння:
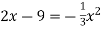 .
.
-
При якому значенні а рівняння
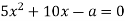 має один корінь?
має один корінь?
-
Розв’яжи рівняння:
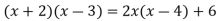 .
.
-
Число – 3 – корінь рівняння
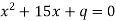 . Знайди
. Знайди 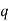 і другий корінь рівняння.
і другий корінь рівняння.
Урок №8
«Діточки, любімо не словом,
ані язиком, але ділом та правдою!»
1послання ап. Івана 3:18
Фронтальне опрацювання матеріалу
Квадратний тричлен та його корені. Розкладання квадратного тричлена на множники
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.12 блоку № 5.
- Усно дай відповіді на запитання:
- Яке рівняння називається квадратним?
- Від чого залежить кількість коренів квадратного рівняння?
- Як записуються формули дискримінанта та коренів квадратного рівняння?
- Як читається теорема Вієта?
- Що називається квадратним тричленом?
- Що називається коренем квадратного тричлена?
- Як записується формула розкладання квадратного тричлена на множники?
Завдання 2.
- Ознайомся з алгоритмом розкладання квадратного тричлена на множники. Запам’ятай його.

- Розглянь приклад:
![]()

ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Користуючись алгоритмом та розглянутим прикладом, виконай вправи:

3.1.
 3.2.
3.2.
- Виконай самостійно:
|
1 варіант |
2 варіант |
|
1. Розклади на множники квадратний тричлен: |
|
|
|
|
|
2. Скороти дріб та обчисли його значення при заданому значенні x: |
|
|
|
|
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач

Завдання 4.
Задача «Страхова компанія»
Кожний менеджер страхової компанії веде однакову кількість справ клієнтів. Усього компанія веде 180 справ. Через реформування компанії трьох менеджерів було звільнено, а справи їхніх клієнтів розподілено між іншими менеджерами, причому кожен отримав 2 нові справи.
- Скільки менеджерів було в компанії спочатку?
- Скільки справ став вести кожний менеджер після реформування компанії?
Уроки №9, 10
«Нехай молодим твоїм віком ніхто не гордує, але будь зразком
для вірних у слові, у житті, у любові, у дусі, у вірі, у чистості!»
1послання ап. Павла до Тимофія 4:12
Фронтальне опрацювання матеріалу
Розв’язування рівнянь, що зводяться до квадратних
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори блок № 5.
- Усно дай відповіді на питання:
- Яке рівняння називається квадратним? Наведи приклад квадратного рівняння.
- Як записується формула коренів квадратного рівняння?
- Коли квадратне рівняння має один корінь; два корені; немає коренів?
- Яке квадратне рівняння називається зведеним?
- Сформулюй теорему Вієта.
- Що називається квадратним тричленом?
- Наведи приклад квадратного тричлена.
- Як записується формула розкладання квадратного тричлена на множники?
Завдання 2.
- Прочитай § 25, стор.206 – 209 підручника.
- Знайди в тексті відповіді на питання:
- Назви найпоширеніші типи рівнянь, розв’язування яких зводиться до квадратних рівнянь та методи їх розв’язування.
- Які рівняння називаються біквадратними?
- Поясни спосіб розв’язування рівнянь кожного типу.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
3.1. Розв’яжіть рівняння:
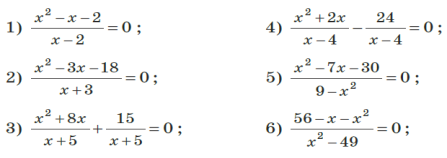
3.2. Розв’яжіть рівняння: 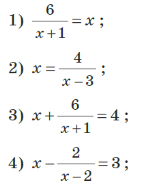
3.3. Розв’яжіть рівняння:
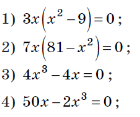
- Знайдіть корені рівняння:
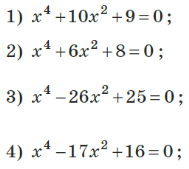
- Розв’яжіть рівняння:

Завдання 4.
4.1. Знайдіть корені біквадратного рівняння:
![]()
4.2. Розв’яжіть рівняння:

4.3. Розв’яжіть рівняння:

Уроки №11, 12
«Поважати людей – означає поважати кожного
із них, а не тільки тих, на кого хочеш справити враження…»
Народна мудрість
Фронтальне опрацювання матеріалу
Розв’язування задач за допомогою квадратних та дробових раціональних рівнянь
І. Робота над засвоєнням понять, означень і правил
Завдання 1.
- Повтори блок № 5.
- Усно дай відповіді на питання:
- Яке рівняння називають квадратним?
- Як дізнатись кількість коренів квадратного рівняння?
- Сформулюй теорему Вієта.
- Яке квадратне рівняння називається зведеним? Наведи власний приклад.
- Як розв’язати задачу за допомогою рівняння?
ІІ. Відпрацювання умінь і навичок, застосування правил.
 Завдання 2.
Завдання 2.
Письмово виконай вправи:
- Софійка та Юрко прикрашали фруктами приготовлені птіфури. Усі тістечка Софійка може прикрасити на 6 хв швидше, ніж Юрко. За який час може прикрасити всі птіфури Юрко, якщо вдвох усі тістечка діти можуть прикрасити за 7,2 хв?
- Валентина посадила 200 кущів самшиту до обіду, висаджуючи щогодини x кущів, та 90 кущів — після обіду, висаджуючи щогодини на 20 кущів менше, ніж до обіду. На всю роботу Валентина витратила 7 год. Знайдіть x.
- Дві бригади робітників клали тротуарну плитку. Кожна бригада мала покласти 2400 плиток. Перша бригада клала x тротуарних плиток щогодини, а друга — на 50 плиток більше. Друга бригада закінчила всю роботу на 4 год швидше, ніж перша. Знайдіть x.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Письмово виконай вправи:
Завдання 3.
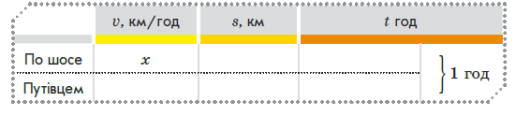
- Під час змагань зі спортивного орієнтування Дмитро подолав 7 км по шосе і 5 км путівцем. По шосе Дмитро рухався зі швидкістю на 4 км/год більшою, ніж путівцем. Визначте швидкість його руху по шосе, якщо на весь шлях Дмитро витратив 1 год.
До розв’язання:
- Літак виконує рейси між Берліном і Києвом, відстань між якими 1440 км. Рейс із Берліна до Києва тривав на 1 год більше, ніж зворотний рейс, оскільки літак рухався зі швидкістю на 72 км/год меншою.
1) Знайдіть швидкість літака під час зворотного рейсу. Вважайте погоду спокійною, знехтуйте швидкістю вітру.
2) Андрій вилетів рейсом із Берліна о 15 : 30 за київським часом. З’ясуйте, чи встиг він того самого дня на концерт у Києві, що розпочався о 19 : 00.
До розв’язання:

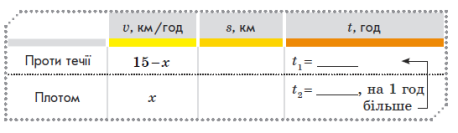
- Турист проплив 10 км проти течії річки на моторному човні, власна швидкість якого становить 15 км/год. Назад турист повернувся на плоту. Відомо, що плотом він плив на 1 год більше, ніж човном.
1) Знайдіть швидкість течії річки.
2) Визначте, скільки часу витратив би турист на зворотний шлях, якби повернувся на човні.
До розв’язання:
Урок №13
«Раджу вам розглядати власні
невдачі як джерело мотивації і натхнення»
Нік Вуйчич, християнський
проповідник, мотиваційний тренер
Фронтальне опрацювання матеріалу
Квадратний тричлен. Рівняння, що зводяться до квадратних. Розв’язування задач за допомогою квадратних рівнянь
І. Робота над засвоєнням понять, означень і правил
Завдання 1.
- Повтори тези 2.10 – 4.16 блоку № 5.
- Усно дай відповіді на питання:
- Що називають квадратним тричленом?
- Що називають коренем квадратного тричлена?
- Як записується формула розкладання квадратного тричлена на множники?
- Яке рівняння називається біквадратним?
- Які є способи розв’язування рівнянь, які зводяться до квадратних?
- Як розв’язати задачу за допомогою рівняння?
ІІ. Відпрацювання умінь і навичок, застосування правил.
Завдання 2.
Усно розв’яжи вправи:
-
Числа 2 і – 4 є коренями квадратного тричлена
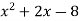 . Тоді
. Тоді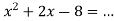
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Якщо у рівнянні
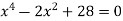 замінити
замінити 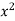 на
на 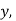 то одержимо рівняння …
то одержимо рівняння …
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайди периметр квадрата площею 144 см². Яке з рівнянь відповідає умові задачі, якщо через
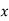 позначити сторону квадрата.
позначити сторону квадрата.
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово виконай вправи:
-
Знайди корені квадратного тричлена:
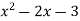 .
.
-
Скороти дріб:
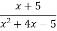 .
.
-
Розв’яжи рівняння: 1)
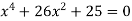 ; 2)
; 2) 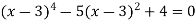 .
.
- Патрульний катер пройшов 72 км за течією річки та повернувся назад, витративши на весь шлях 7 год. Знайдіть власну швидкість катера, якщо швидкість течії річки дорівнює 3 км/год.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
Знайди корені квадратного тричлена:
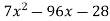 .
.
-
Скороти дріб:
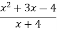 .
.
-
Розв’яжи рівняння:
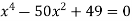 .
.
- Пасажирський поїзд проходить відстань, що дорівнює 480 км, на 4 год швидше, ніж товарний. Знайди швидкість пасажирського поїзда, якщо швидкість товарного на 20 км/год менша від швидкості пасажирського.
Урок №15
«Хто добре запалився, той добре почав,
а добре почати – це наполовину завершити»
Григорій Сковорода
Внутрішньопредметне узагальнення матеріалу
Квадратні рівняння
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 5.
- Дай письмово відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
-
Знайди корені рівняння:
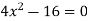 .
.
|
А |
Б |
В |
Г |
|
– 1; 1 |
– 2; 2 |
– 3; 3 |
– 4; 4 |
-
Не розв’язуючи рівняння
 , знайди суму його коренів.
, знайди суму його коренів.
|
А |
Б |
В |
Г |
|
– 8 |
8 |
– 1 |
1 |
- Коренями якого з наведених рівнянь є числа 3 і – 4?
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово виконай вправи:
-
За допомогою теореми Вієта знайди корені рівняння:
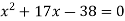 .
.
-
Розклади на множники квадратний тричлен:
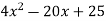 .
.
-
Розв’яжи рівняння:
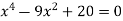 .
.
-
Скороти дріб:
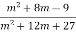 .
.
- Перші 40 км шляху велосипедист рухався зі швидкістю, яка на 5км ∕ год більша за швидкість, з якою він долав останні 40 км. З якою швидкістю проїхав велосипедист другу половину шляху, якщо на весь шлях він витратив 6 год 40 хв?
Урок №17
«Єдиний шлях, що веде до знань – це діяльність.
Бернард Шоу
Міжпредметне узагальнення матеріалу
Урок – квест «Квадратні рівняння»
Мета: систематизувати здобуті знання, формувати практичні навики їх використання, вміння аналізувати, критично мислити, працювати в команді, виховувати відповідальність, упевненість в собі, волю до перемоги, досягнення успіху у житті
Обладнання: мультимедійна система, ресурс Learningapps, додаток Документ Google, програма для зчитування QR-коду, картки із завданнями, маршрутні листи для команд
Місце проведення: кабінет математики
Підготовча робота: клас поділений на 6 команд, кожна команда обирає капітана; учнівські парти розміщені так, щоб дітям зручно було працювати на станціях; на партах назви станцій «Дослідження», «Теорема Вієта», «Історична», «Інтерактивна», «Цікаве рівняння», «QR-код»; кожна команда працює вдома по історичному матеріалу, пов’язаному з темою «Квадратні рівняння»; на Google Диску створено секторну діаграму з спільним редагуванням для підведення підсумків квесту; підготувати на станції консультантів
Хід уроку
І. Організаційний момент
Учитель: Доброго дня, діти! Ми сьогодні проведемо з вами урок-квест. Що таке квест, я впевнена, ви знаєте. Поділіться своїми знаннями. (Діти розповідають, що вони розуміють під словом «квест»).
Отже, команди готові до роботи, і ми можемо вирушати в подорож по країні «Квадратні рівняння». Не забудьте взяти з собою гарний настрій, спрямований тільки на перемогу; відповідальність, взаємоповагу і бажання зміцнити свої знання і відкрити для себе нове! Кожна команда рухається по шести станціях, перемагає та, яка перша відкриє всі таємниці! Капітани команди, отримайте маршрутні листи (Додаток 1) і починаємо подорож!
ІІ. Подорож по станціях
- «Цікаве рівняння»
Розв’яжіть рівняння:
![]()
Консультанти перевіряють правильність і роблять відмітку у маршрутному листі кожної команди. (Відповіді подані у Додатку 2).
- «Дослідження»
Що буде, якщо в квадратному рівнянні ах2 + bx + c = 0 поміняти
місцями a і c?
Для дослідження використайте рівняння:
х2 – 6х + 5 = 0
5х2 – 9х – 2 = 0
- «Інтерактивна вправа»
Розділіть рівняння на групи по кількості їх коренів.
Вправа виконується на комп’ютері, перевіряється автоматично.
https://learningapps.org/view4563471
- «Теорема Вієта»
Заповніть таблицю, використовуючи теорему Вієта.
|
Рівняння |
Сума коренів |
Добуток коренів |
|
х2 – 6х + 5 =0 |
|
|
|
3х2 + 3х ‒ 5 =0 |
|
|
|
0,2х2 – 8х + 5 =0 |
|
|
|
|
8 |
12 |
- «Історична станція»
Встановіть відповідність між історичним фактом і особистістю.
|
Питання |
Відповіді |
|
А. Вієт |
|
2. Відкрив правило знаходження коренів рівняння ах2 +bх = с |
Б. Діофант |
|
3. Вивів формулу залежності коренів рівняння від коефіцієнтів |
В. Брахмагупта |
|
4. Вивів загальне правило розв’язування квадратних рівнянь |
Г. Штифель |
|
5. Запропонував формулу дискримінанта |
Д. Піфагор |
|
|
Е. Сільвестр
|
-

«QR- код»
Прочитайте вислів і поясніть його важливість.
ІІІ. Підсумок уроку
Команди звітуються про виконані завдання, розповідають, що було найважче виконати, над чим ще треба попрацювати.
На якій станції було найцікавіше працювати показують на секторній діаграмі, яка створена в Документі Google і для якої відкритий доступ для спільного редагування. Учні виходять до інтерактивної дошки і перетягують трикутник до певного сектора.
Посилання для спільного доступу
Додаток 1
Маршрутні листи команд
Команда № 1
|
Станції |
Відмітка про виконання |
Бали |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Команда № 2
|
Станції |
Відмітка про виконання |
Бали |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Команда № 3
|
Станції |
Відмітка про виконання |
Бали |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Команда № 4
|
Станції |
Відмітка про виконання |
Бали |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Команда № 5
|
Станції |
Відмітка про виконання |
Бали |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Команда № 6
|
Станції |
Відмітка про виконання |
Бали |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Додаток 2
Відповіді
Станція «Цікаве рівняння»
х = -0,4, х ≠ 1.
Станція «Історична»
- – Б, 2 – В, 3 – А, 4 – Г, 5 –Е.
«Теорема Вієта»
|
Рівняння |
Сума коренів |
Добуток коренів |
|
х2 – 6х + 5 =0
|
6 |
5 |
|
3х2 + 3х ‒ 5 =0
|
|
|
|
0,2х2 – 8х + 5 =0
|
40 |
25 |
|
|
8
|
12 |
Станція «Дослідження»
Корені будуть оберненими до коренів даного рівняння
Станція «QR- код»
Вислів:
Найкращий спосіб вивчити що-небудь – це відкрити самому.
Д. Пойа
Тема №6. Повторення матеріалу, вивченого протягом року
Уроки №1, 2
«Любіть своїх ворогів, добро робіть тим,
хто ненавидить вас. Благословляйте тих,
хто вас проклинає, і моліться за тих,
хто кривду вам чинить»
Луки 6:27,28
Внутрішньопредметне узагальнення матеріалу за рік
Завдання 1.
Усно виконати вправи:
-
Виконайте множення
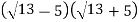 .
.
|
А |
Б |
В |
Г |
|
8 |
18 |
– 12 |
12 |
-
При яких значеннях х не має змісту вираз
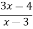 ?
?
|
А |
Б |
В |
Г |
|
|
– 3 |
3 |
|
-
Чому дорівнює сума коренів квадратного рівняння
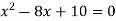 ?
?
|
А |
Б |
В |
Г |
|
– 10 |
10 |
– 8 |
8 |
Завдання 2.
Письмово виконати вправи:
-
Скоротіть дріб
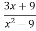 .
.
-
Розв’яжіть рівняння
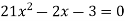 .
.
-
Знайдіть значення виразу
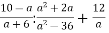 , якщо
, якщо  .
.
-
Спростіть вираз
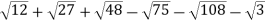 .
.
- Два робітники, працюючи разом, можуть виконати роботу за 12 днів. Перший, працюючи окремо, може виконати цю роботу на 7 днів швидше, ніж другий. За скільки днів виконає роботу кожен робітник, працюючи окремо?
Завдання 3.
Усно виконати вправи:
-
Виконайте множення
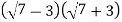 .
.
|
А |
Б |
В |
Г |
|
8 |
18 |
– 2 |
2 |
-
При яких значеннях х не має змісту вираз
 ?
?
|
А |
Б |
В |
Г |
|
|
– 4 |
4 |
|
-
Чому дорівнює сума коренів квадратного рівняння
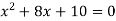 ?
?
|
А |
Б |
В |
Г |
|
– 10 |
10 |
– 8 |
8 |
Завдання 4.
Письмово виконати вправи:
4.1. Скоротіть дріб ![]() .
.
-
Розв’яжіть рівняння
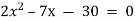
-
Знайдіть значення виразу
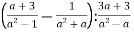 , якщо
, якщо 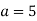 .
.
-
Спростіть вираз
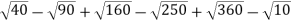 .
.
- Два маляри, працюючи разом, можуть пофарбувати фасад будинку за 16год. За скільки годин може виконати цю роботу кожен з них , працюючи самостійно, якщо одному з них для цього потрібно на 24год менше, ніж другому?



про публікацію авторської розробки
Додати розробку