Посібник. Літня інтелектуальна школа «АЛЬФА + ОМЕГА»

Управління освіти і науки Луцької міської ради Луцька гімназія № 4 імені Модеста Левицького

Методичне об’єднання вчителів математики

 

Шеретюк Н.В., Цейко Г.М.

 

Методичні рекомендації

 

 

 

 

Луцьк 2016 р.
Схвалено колегією науково-методичного центру Луцької гімназії №4 імені

 Модеста Левицького (протокол №5 від 11 лютого 2016 року).

 

 

 

 

 

 

 

В методичних рекомендаціях обґрунтовано важливість розвитку творчого мислення учнів у процесі вивчення математики, зокрема в позаурочний час. Висвітлено зміст та організацію роботи літньої інтелектуальної школи «АЛЬФА + ОМЕГА» за проектними технологіями «Метаморфози паперу» та «Літо інтелекту».

Посібник буде корисний вчителям математики та студентам педагогічних закладів освіти.

 

 

 

 

 

 

 

 

 

 

 

Рецензенти:

Трачук Т. В. – доцент кафедри теорії та методик викладання шкільних предметів ВІППО, кандидат педагогічних наук.

Дудик Л. М. – вчитель  вищої категорії Луцької гімназії №4 імені Модеста Левицького, вчитель-методист.

 

 

 Шеретюк Н. В., Цейко Г. М. 

Літня інтелектуальна школа «АЛЬФА + ОМЕГА»

Методичні рекомендації. – Луцьк. 2016. – 73 с.

ЗМІСТ

 

ВСТУП………………………………………………………………………………4

РОЗДІЛ 1. Навчання як творчий процес………………………………………..6

1.1.Творчість від вчителя до учня..............................................................................6

1.2.Відпочинок поруч з математикою.......................................................................9

РОЗДІЛ 2. Літня інтелектуальна школа «АЛЬФА + ОМЕГА»….....……….10

2.1.Проект «Метаморфози паперу» (5-8 класи).....................................................11

2.1.1. Мета та завдання проекту…………………………………………………...13

2.1.2. Виникнення та розвиток орігамі…………………………………...………17

2.1.3. Легенди про орігамі……………………………………………………...….19

2.1.4. Види і техніки орігамі……………………………………………...………22

2.1.5. Орігаметрія як нова математична теорія………………………….……….33

2.1.6. Розв’язування геометричних задач методом перегинів………………..…36

2.1.7. Застосування орігамі в науці і житті………………………………………46

2.2. Проект «Літо інтелекту – відпочинок з математикою» (10 класи) ...............48

2.2.1. Турнірна задача як елемент спільної дослідницької

           діяльності науковців, учителів та учнів ......................................................50

2.2.2. Як правильно розподілити ролі в турнірній грі .........................................54

2.2.3. Зразки доповідей міського турніру, які підготували учні

           Луцької гімназії № 4 імені Модеста Левицького ......................................58

2.2.4. Як опонувати та рецензувати.........................................................................68

2.2.5. Гордість Луцької гімназії № 4 імені Модеста Левицького ........................70

CПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ.............................................................73

ВСТУП

 

Творчості, як і будь-якої діяльності, можна навчитися.
Г. Альтшуллер

 

Не секрет, що математика завжди вважалася і вважається одним із найскладніших предметів, однак не можна переоцінити її особливу роль у розвитку мислення, формуванні творчої особистості. Повноцінне навчання математики у сучасному розумінні має за мету не лише отримання дітьми ґрунтовних знань, але й озброєння їх умінням застосовувати знання творчо, нестандартно, постійно поповнювати систему знань; знаходити оригінальні методи, способи, прийоми розв’язування завдань та проблем; критично оцінювати результати власної діяльності. Математична освіта є стратегічним ресурсом розвитку цивілізації, оскільки під час вивчення саме цього предмету закладаються основи для того, щоб школяр у майбутньому став активним, самостійним і відповідальним суб’єктом власної професійної діяльності.

Запалити в учнів бажання вчитися – основне завдання кожного творчого вчителя. І зробити це доцільно на етапі мотивації навчальної діяльності. Навчання стане творчим процесом, якщо воно буде сплановане на творчу діяльність самих учнів. Навчання не має зводититися лише до засвоєння готових правил і визначень, а повинно бути справжнім процесом "здобуття знань". Для цього потрібно, щоб навчання планувалось як процес постановки і вирішення системи творчих задач.

Творчість – це людська діяльність, у процесі якої особистість, задовольняючи потреби в реалізації своїх здібностей, створює нові знання, об’єкти, схеми поведінки, робить власні «відкриття». Головний закон усіх змін – творчість. Тільки творчість надає сенс життю людини. Для розвитку інтелектуально-творчих здібностей необхідний як певний рівень розвитку цих здібностей, так і мотиви, і риси особистості, характерні для творчих людей, що з’являються на тлі загального мотиваційного розвитку особистості. Іншими словами, творчих якостей  розуму на порожньому місці не буває.

Український психолог  В. Моляко зазначає, що «під творчістю розуміють процес створення чогось нового для даного суб’єкта . Тому зрозуміло, що творчість у тій чи іншій формі не є талантом «вибраних», вона доступна кожному. І школяр, який засвоює нові знання, розв’язує нову, незнайому задачу, і робітник, який виконує нове технічне завдання, і комбайнер, якому потрібно в процесі збору врожаю  врахувати  вологість колосся, напрямок вітру – всі вони займаються творчістю, розв’язують творчі завдання».         

         На протязі багатьох років Луцька гімназія№ 4 імені Модеста Левицького успішно реалізує модель школи – школи підтримки обдарованих учнів. Для того щоб активізувати позакласну роботу, вчителі математики постійно шукають і знаходять нові форми роботи: шкільні наукові конферен­ції, робота в Малій академії наук, інтелектуальні ігри, турніри юних математиків, математичні бої.

Нові творчі турнірні задачі спонукали вчителів математики нашої гімназії продовжити роботу з обдарованими учнями влітку. Тому в гімназії було організовано літню математичну школу, залучивши до неї як старшокласників так і учнів середньої ланки.

Наводимо деякі рекомендації по умовах перебування в літній інтелектуальній  школі, режиму дня, змісту занять. А особливу увагу звертаємо на методику підготовки учнівських команд до турнірів з математики. Адже, турнір - це командні змагання учнів у здатності розв’язувати спільними зусиллями складні математичні проблемні завдання, подавати розв’язок у переконливій формі та захищати свій варіант розв’язку завдань у науковій дискусії (математичному бою), аргументовано відстоювати свою точку зору на проблеми, пов’язані з завданнями турніру, кваліфіковано опонувати відповіді інших команд. Рекомендуємо як можна влітку зацікавити школярів, залучивши їх до творчого розв’язування задач за допомогою згинів паперу та як зробити класичні фігури орігамі та орігамі з модулів.

РОЗДІЛ 1.  НАВЧАННЯ ЯК ТВОРЧИЙ ПРОЦЕС

 

1.1. Творчість – від вчителя до учня

Надання учням радості праці, радості успіху у навчанні, збудження в їхніх серцях почуття гордості, власної гідності, віри в себе – це важливе завдання вчителя. І лише в таких умовах можуть розвиватися творчі здібності учнів. Головна особливість творчої людини – це віра у власні сили та у свої можливості. Як тільки людина повірить в це – в неї відкривається творче начало. І його ніхто потім не може заглушити.

Саме про це говорив В.О. Сухомлинський: «У наших школах не повинно бути нещасливих учнів, душу яких гнітить думка, що вони ні на що не здібні. Успіх у навчанні – єдине джерело внутрішніх сил учня, які породжують енергію для долання труднощів, бажання вчитися».

Навіть разове переживання успіху може докорінно змінити психологічне самопочуття учня. Адже успіх – спусковий механізм подальшого творчого руху особистості.

Процес творчості – це перш за все відкриття нового: нових об’єктів, нових знань, нових завдань та методів їх вирішення. Навчання як творчий процес – це вирішення нестандартних навчальних задач нестандартними методами, в ході яких учні засвоюють нові знання, уміння та навички спілкування.

Здатність вчителя організовувати спілкування є основою продуктивної, творчої діяльності учнів. Спілкування стимулює творчий процес. Педагогічна практика свідчить про те, що тільки знання, набуті самостійною працею, роблять випускника здатним творчо вирішувати проблеми.

Очевидно, що життя вчителя – це обов'язок бути світочем, утверджувати ідеали правди, краси, добра. Учитель – це той, хто сіє добре зерно. Щастя для нього – гідні учні, які сяють, як сонце, наслідуючи його чесноти та продовжуючи його доброчинність. Та природно, що активність учня не лише самобутня, а й стимульована прикладом учителя. Як же розвивати творчі можливості?

Важливим завданням ефективного розвитку творчих можливостей є створення необхідних умов для їх розвитку. Чим частіше дитина досягає найвищої «планки» успіху, тим успішніше розвиваються її можливості. Дуже важливо, щоб вона мала свободу у виборі діяльності, способів роботи, шляхів досягнення мети. Учитель же повинен пропонувати ненав'язливу допомогу, розумну, доброзичливу, тактовну. Тільки за таких умов можливий розвиток творчих можливостей

В сучасному житті, яке характеризується стрімкими змінами у різних його сферах – політичній, економічній, науковій і культурній, особливого значення набувають уміння людини самостійно та нестандартно мислити, прогнозувати результати, виявляти творчий підхід у будь-якій діяльності.

Тому розкриття творчого потенціалу, створення оптимальних умов для самореалізації особистості, тобто розвиток творчості їх обдарованості є одне з пріоритетних.

Обдарованість – складне, багатогранне явище. Кожна обдарована дитина– індивідуальність, що потребує особливого підходу. Під час роботи з такими дітьми постійно виникають педагогічні й психологічні труднощі, обумовлені розмаїтістю видів обдарованості, зокрема віковою та прихованою, безліччю суперечливих теоретичних підходів і методів, варіативністю сучасної освіти. Працюючи з обдарованими дітьми, педагог повинен уміти вставати в позицію рефлексії до самого себе. Так, одним з основних психологічних принципів роботи з дітьми є принцип «прийняття іншого», згідно з яким учитель повинен спочатку приймати учня як індивідуальність зі своїми особливостями, що вже склалися. Крім того, вчителеві важливо володіти даром навіювання, вміти аргументовано переконувати; бути неупередженим, справедливим, емоційно врівноваженим, тактовним, щоб не вплинути негативно на прагнення дитини до творчості, на її етичні вчинки; бути здатним до самоаналізу, самокритики, перегляду своїх позицій, виваженості вчинків; налагоджувати з учнями партнерські стосунки; надавати дітям свободу вибору і прийняття рішень; володіти високим рівнем пізнавальної і внутрішньої мотивації, адекватною самооцінкою тощо. Як відомо, лише особистість може виховати особистість і тільки талант може виростити новий талант.

 Саме вчитель створює атмосферу, яка може надихати учня або руйнувати його впевненість у собі, заохочувати чи пригнічувати інтереси. Щоб створити таку атмосферу, варто використовувати такі творчі методи:

• стимулювати бажання учнів працювати самостійно;
• заохочувати до роботи над проектами, запропонованими самими учнями;
• переконувати учнів у тому, що вчитель є їхнім однодумцем;
• заохочувати до максимальної захопленості у спільній діяльності;
• виключати будь-який тиск на дітей, створювати розкуту атмосферу;
• надавати дитині свободу вибору галузі застосування своїх здібностей.

Адже обдарований учень починається з обдарованого вчителя (інтелект загострюється інтелектом, характер виховується характером, особистість формується особистістю). Завдання педагога - управляти процесами творчого пошуку, йдучи від простого до складного: створювати ситуації, що сприяють творчій активності та спрямованості школяра, розвивати його уяву, асоціативне мислення, здатність розуміти закономірності, прагнення постійно вдосконалюватися, розв'язувати дедалі складніші творчі завдання.

А якою ж має бути мотивація навчальної діяльності учнів?

Математика більшості дітям дається нелегко. Для таких учнів залучення до загальнолюдської культури – дуже слабкий, мало дієвий мотив навчання. А якщо в учня немає мотивів вивчати математику або ці мотиви слабкі, його навчання перетворюється на безцільну муку. Усунути цю причину можна лише одним способом – своєчасно сформувати дієві мотиви учіння. Учні мають усвідомлювати, що матеріал, який вивчається на уроках математики, знадобиться їм не лише для розвитку їхньої загальної культури, а й безпосередньо у практичній діяльності та просто в житті.

1.2. Відпочинок поруч з математикою

В Україні функціонує багато наукових літніх шкіл: дистанційні літні школи, багатопрофільні школи при фізико-математичних ліцеях, наукові літні школи Малої академії наук України. Літня школа – різновид річного шкільного табору, в якому поєднуються літній відпочинок і активні заняття в тій чи іншій галузі науки. Велика роль відводиться неформальному спілкуванню школярів, студентів і викладачів, як на наукові теми, так і на загальнолюдські. У літніх школах проводяться спортивні заняття, екскурсії, свята, заняття творчою самодіяльністю.

На базі нашої Луцької гімназії № 4 імені Модеста Левицького влітку 2015 року була створена літня інтелектуальна  школа «АЛЬФА + ОМЕГА». Для учнів 5-8 класів було розроблено проект «Метаморфози паперу», а для учнів 10-х класів «Літо інтелекту - відпочинок з математикою».

Мета літньої наукової школи: стимулювати учнів до інтелектуального розвитку, забезпечити мотиваційне середовище для усвідомлення науково-дослідної діяльності,  забезпечити інтелектуальне зростання, розвиток творчого потенціалу,  створити умови, необхідні для розвитку індивідуальності учнів, усвідомлення ними свого образу «Я»,  формувати позитивний імідж гімназії.

Літня наукова школа - це не тільки школа навчання, й школа відпочинку.

Не всі учасники літньої наукової школи стануть науков­цями. Але жага знань та вміння їх здобувати залишаться з ними на все життя. Тільки шляхом самоосвіти можна чогось навчитись. І наше завдання полягає в тому, щоб допомогти дітям самостійно отримувати знання. Це — шлях до створення кращих можливостей для самореалізації обдарованих дітей, атмосфери наукового спілкування. У майбутньому їм знадобляться здобуті знання, навички пошукової, дослідної роботи, вміння самостійно здійснювати експерименти, працювати з науковою літературою. Діти бачать перспективу особистісного розвитку, обирають своєрідні ідеали, у них виникає необхідність у науковому пізнанні та дослідництві. Це стає їхньою внутрішньою потребою, умовою самореалізації.

РОЗДІЛ 2. ЛІТНЯ ІНТЕЛЕКТУАЛЬНА ШКОЛА «АЛЬФА + ОМЕГА»

 

З 8 червня по 18 червня  щороку учні гімназії мають можливість забезпечити інтелектуальне зростання, покращити та вдосконалити знання з математики, пізнати математику в світі прекрасного, навчитись робити математичні дослідження з теми, яка припала до душі. Математична літня школа включає заняття для учнів 5-8 класів та 10-х класів.

Пропонуються теми для опрацювання:

• відпочинок (спорт, мистецтво і наука);
• розв’язування олімпіадних, турнірних задач та задач ЗНО;
• підготовка учнів до турнірів; 
• розв’язування  задач за допомогою перегину паперу;
• робота над орігамі, фігури орігамі;
• математика навколо нас (світ прекрасного, світ природних явищ).

 

Умови перебування у літній інтелектуальній школі

«АЛЬФА + ОМЕГА»:

1. Літня математична школа працює з 10.00 по 13.30 год. з 08.06. по 19.06. року (крім суботи та неділі).
2. Режим дня:

10.00 – 10.30  Прийом, організація дітей. Сніданок.

10.30 – 11.30  Робота у групах над виконанням проектів.

11.30 – 12.00  Перерва. Рухливі ігри на шкільному майданчику.

12.00 – 13.00  Активні заняття з використанням елементів змагання.

13.00 – 13.30  Обід. Завершення роботи.

3. Групи формуються відповідно до віку (5-8 класи; 10 класи).
4. Орієнтовна вартість харчування – 14 грн. в день.
5. Одноразовий внесок у розмірі 20 грн. на канцтовари.
6. Щоп’ятниці презентація учнівських проектів в кабінетах №43, №16 гімназії.  Запрошуються батьки.

2.1. Проект «Метаморфози паперу» (5-8 класи)

Орієтовний план проекту

Понеділок    

І. Знайомство учнів в команді.

1.               Гра на знайомство «Інтерв’ю».
2.               Інтелектуальна вікторина.

ІІ. Поділ на групи. Назви груп.

1.               Вибираємо навчальний проект «Метаморфози паперу».
2.               Визначення правил роботи.
3.               Розподіл обов’язків.

Вівторок  

І. Змістовне (історичне) насичення до проекту.

1.               Звідки прийшло орігамі?
2.               Як можна виміряти красу законами геометрії?
3.               Як можна вивчати геометрію через орігамі?
4.               Як можна розв’язати задачу за допомогою згинів паперу?

Середа 

І. Наглядне ознайомлення з орігамі.

1.               Легенди, казки орігамі.
2.               Орігамі – мистецтво складання з паперу.
3.               Аксіоми орігамі.

Четвер   

І. Практичне насичення проекту.

1.               Задача про поділ квадрата на рівні частини.
2.               Задача на побудову правильних многокутників.
3.               Цікаві геометричні задачі.

П’ятниця

І. Створення проекту.

1.               Як зробити прості орігамі з паперу (стаканчик, класичний журавель, лебідь, голуб, жабка, тюльпан).
2.               Розподіл доручень по створенню фігур орігамі.
3.               Презентація простих фігур орігамі.

Понеділок   

І. Створення проекту.

1.               «Як зробити модуль орігамі».
2.               Виготовлення різнокольорових модулів орігамі.
3.               Виведення формул площ методом перегину паперу.

Вівторок   

І. Створення проекту.

1.               Прості базові форми орігамі «трикутник» та «подвійний трикутник». Презентація форм.
2.               Виготовлення базових форм.
3.               Застосування методу орігаметрії при розв’язуванні задач на побудову, доведення.

Середа    

І. Створення проекту.

1.               Як зробити орігамі з модулів.
2.               Виготовлення фігур з базових модулів.
3.               Задачі-жарти.

Четвер     

І. Презентація проекту.

1.               Виготовлення фігур з базових модулів.
2.               Виставка-конкурс фігур з орігамі.
3.               Захист творчих проектів.

П’ятниця     

І. Підсумки проекту.

1.               Короткий зміст.
2.               Ставлення до проекту.
3.               Запитання – відповіді.

ІІ. Нагородження.

2.1.1. Мета та завдання проекту

У світі немає місця для некрасивої математики.

Готфрід Харді, математик

Геометрія – один із найважливіших розділів шкільного курсу математики. Саме геометрія допомагає розвинути логічне мислення, просторову уяву учнів, застосувати математику до практичної діяльності людини. Досвід показує, що наочність при вивченні курсу геометрії дозволяє учням якісно і свідомо засвоїти геометричні поняття і методи розв'язування задач, що важче досягається шляхом усталеного академічного лекційного викладу тільки на рівні уяви. Особливого значення для підвищення пізнавальної активності та мотивації учнів до навчання набуває можливість самостійної геометричної побудови або конструювання. Конструювання учнями виробів з паперу, долучення до мистецтва орігамі допоможуть їм краще засвоїти такі важливі геометричні поняття як симетрія, рівність фігур, тривимірний простір, навчать аналізувати, обґрунтовувати, відкривати і доводити властивості геометричних фігур. Орігамі сприятиме створенню наочної моделі евклідової геометрії та допоможе побачити в академічній науці мистецтво.

Орігамі знайомить з усіма геометричними об’єктами і полегшує вивчення курсу геометрії. Вивчення перетворень квадратного та прямокутного аркушів паперу, можливо, один із найбільш цікавих шляхів створення образів плоских і об’ємних фігур. Тут об’єктом безпосередніх перетворень є реальна ситуація. Крім цього, даний метод є корисним заняттям.

В процесі розв’язування задач методом перегину паперу відбувається природний масаж кінчиків пальців рук. Це унікальний засіб для розвитку тонкої моторики і чутливості пальців. Активна робота обома руками спонукає активно працювати головний мозок.

Під час роботи з папером діти без перевантаження, з радістю виконують різноманітні завдання, які розвивають просторову уяву, графічні навички, руховий стереотип, уміння аналізувати малюнок за зразком та розвивають акуратність, координацію та ритм рухів, окомір, точність, дрібні м'язи рук, зап'ястя.

Конструювання при ознайомленні з наукою «Орігаметрія» дозволить учням сприймати геометрію не тільки як академічну науку, а ще й як науку мистецтва, творчості і краси, що підвищить мотивацію учнів до навчання геометрії і розуміння її місця в житті та діяльності людини, дозволить урізноманітнити навчальну діяльність.

В геометрії все починається з точки, прямої, відрізка, потім – трикутник, квадрат, а далі – піраміда, куб, паралелепіпед. Аналогічно і в орігамі відбувається розвиток від ліній (так званих умовних знаків), до форм складання листа: трикутник, ромб, подвійний квадрат і вже потім самі моделі орігамі.

Коли створюються фігурки - орігамі, то учні згадують такі поняття, як середина відрізка, діагональ квадрата, трикутник, центр фігури, рівність відрізків, бісектриса, перпендикуляр, третина відрізка та інші.

Методами орігамі, тобто лише перегинами аркуша паперу, можна розв’язати будь-які задачі на побудову, які розв'язуються за допомогою класичних інструментів - циркуля і лінійки.

Орігамі – цікавий спосіб краще зрозуміти геометрію. Тому елементи орігаметрії необхідно застосовувати на уроках математики. Так, під час вивчення теми «Кути та їх міри» доцільно з учнями спочатку на квадратному аркуші паперу розглянути кути 180°, 90°, 45°, 30°, а потім будувати за допомогою транспортира.

Вивчаючи тему «Ознаки паралельності прямих» та «Сума кутів трикутника» можна задати домашнє завдання учням довести теореми методом перегину паперу.

Пояснюючи учням тему «Рівнобедрений трикутник», можна методом перегину паперу довести теорему про бісектрису, проведену до основи трикутника. Для цього достатньо вирізати із паперу прямокутний, гострокутний, тупокутний рівнобедрені трикутники. Перегинаючи їх по бісектрисі кута при вершині можна побачити доведення даної теореми.

Побудову многокутників при вивченні теми «Правильні многокутники» можна також побудувати орігамним методом. Схеми побудови правильних многокутників легко зрозуміти і використати в роботі.

А що вже говорити про 11 клас, коли вивчається тема «Многогранники»… Неоціненну допомогу у виготовленні многогранників може принести орігамі. Складання многогранників - захоплююче заняття, але разом з тим і не просте. Воно вимагає акуратності, точності і високого зосередження уваги. Тільки три многогранники: тетраедр, куб і октаедр можна скласти з одного квадратного аркуша паперу. Решта збираються з декількох модулів.

Ще в античності були поставлені такі три задачі на побудову:

• Трисекція кута – розбити довільний кут на три рівні частини.
• Подвоєння куба – побудувати відрізок, що є ребром куба вдвічі більшого об'єму, ніж куб з даним ребром.
• Квадратура круга – побудувати квадрат, рівний за площею даному кругу.

У XIX столітті було доведено, що всі три задачі нерозв'язні циркулем та лінійкою. На сьогоднішній день перші дві задачі можна розв’язати орігамним методом. Дані задачі можна запропонувати розв’язати учням на факультативних заняттях з математики або під час предметного тижня оголосити конкурс.

Квадратний аркуш паперу є незрівнянним матеріалом для практичного вивчення геометрії. В руках дитини плоска фігура може з легкістю перетворитися в об'ємну, демонструючи графічні елементи без використання креслярських інструментів.

Навчальний проект «Метаморфози паперу» запропонований для учнів 5-8 класів.

Мета: розвиток геометричного та образного мислення, просторової уяви учнів, формування геометричних знань шляхом побудов за допомогою аркуша паперу, творчий розвиток особистості.

Завдання проекту: унаочнити вивчення геометрії, сприяти реалізації її прикладної спрямованості, формувати основні навички в мистецтві орігамі, надати початкові відомості про просторові фігури.

Обладнання: мультимедійний проектор, телевізор, комп'ютери, білий папір, кольоровий папір, ножиці, клей.

Методичні матеріали:

• Презентація вчителя
• Техніка безпеки при роботі з ножицями
• Джерела інформації

Ключове питання

Орігамі - це мистецтво чи наука?

Діяльність учнів

Учні познайомилися зі стартовою презентацією, вибрали напрямки для досліджень,ознайомилися зі списком джерел інформації та правилами техніки безпеки.

За напрямком дослідження: орігамі - це мистецтво

• Познайомилися з історією орігамі
• Підібрали легенди, казки орігамі
• Відшукали в мережі Інтернет схеми фігур орігамі
• Організували виставку робіт орігамі
• Оформили результати досліджень у вигляді презентації

За напрямком дослідження: орігамі - це наука

• Вивчили аксіоми орігамі
• Розглянули застосування методу орігаметрії при розв’язуванні задач на побудову, доведення, обчислення
• Побудували правильні многокутники методом перегину паперу

• Провели математичне обґрунтування побудов
• Розглянули застосування орігамі в науці і житті
• Оформили дослідження у вигляді презентації

2.1.2. Виникнення та розвиток орігамі

Оріґамі (яп. 折り紙 орі – «складати», камі – «папір», тобто «складений папір») – мистецтво складання паперу. Метою цього мистецтва є створення витворів шляхом використання схеми геометричних згинів і складок. Термін оріґамі відноситься до всіх типів складання паперу, а не тільки японських зразків.

В оріґамі використовуються небагато різних згинів, але вони можуть бути скомбіновані багатьма способами й утворювати дуже складні фігури. Зазвичай фігури оріґамі складають без розрізів з квадратного аркуша, сторони якого можуть бути різних кольорів. Усупереч найпоширенішій версії, у традиційному японському оріґамі, що сягає ери Едо (1603–1867), цих правил суворо не дотримувались і в багатьох випадках аркуші розрізали (Кіріґамі 切り紙) або фігури складали не з квадратного аркуша, а з прямокутного, круглого, трикутного тощо.

Хоча, щодо походження оріґамі є деякі розбіжності, але напевно можна сказати, що розвинулось оріґамі саме в стародавньому Китаї, в 105 році н. е. з’явилися перші послання для виникнення орігамі – мистецтва складання улюблених фігурок з квадратного аркуша паперу без використання ножиць та клею.

Як свідчить історія, в тому знаменитому році чиновник Цай Лунь зробив офіційну доповідь імператору про створення технології по виготовленню паперу. Багато десятиліть під острахом смертної кари китайці зберігали таємницю створення білого аркуша. Але з часом, коли китайці почали подорожувати до Японії, разом з ними подорожували й деякі таємниці цієї країни. В 7 ст. Буддійський монах Дан-Хо, якого вважали дуже розумним, і який знав технологію виготовлення туші та паперу, потрапляє в Японію і навчає монахів виготовляти папір за китайською технологією. Дуже скоро в Японії зуміли налагодити своє виробництво  паперу, випередивши Китай.

Перші аркуші паперу, складені в незвичайні фігурки з’являються спочатку в монастирях. Тому що в японській мові поняття «Бог» і «Папір» звучать однаково, хоч і позначаються різними ієрогліфами. Фігурки з паперу ставали учасниками релігійних церемоній. Прикрашали стіни храмів. До сьогодення дійшли одні з перших фігурок з паперу – коробочки «санбо», в які японці клали кусочки риби та овочів, і підносили їх в якості жертвопринесення. Але це ще було не мистецтво. Просто аркуш паперу, дуже цінний і дорогий, що несе в собі ім'я Бога, ставав невід'ємною частиною життя японця. Просто аркуш паперу, дуже цінний і дорогий, що несе в собі ім'я Бога, ставав невід'ємною частиною життя японця.

В середні віки, коли виробництво паперу дозволило знизити на неї ціну, мистецтво складання проникло в побут дворянства. І тоді з'явилося мистецтво самураїв. У ті часи вважалося ознакою хорошого виховання уміння багатого дворянина розважити свою даму на балу складанням паперових фігурок. Тоді ж виникло і мистецтво згортання таємних листів. Використовуючи своє вміння, самураї так складали свої записки, що тільки той, кому вона призначалася, міг розвернути її.

З часом орігамі (а цей термін виник тільки в 1880 році) стає обов’язковим заняттям в багатьох японських сім’ях. Матері передавали свої знання дочкам, показуючи відомі їм фігурки.

В перекладі з японської орігамі означає «складання паперу». Саме орігамі в Японії називають мистецтвом цілого аркуша.

Мистецтво орігамі існувало багато століть як храмове. Кількість фігурок була невелика.

Якщо звернутися до історії різних країн, то практично усюди, де існувало виробництво паперу, виникли свої традиції складання з аркуша паперу різних фігурок. Наприклад, Північна Африка чи Латинська Америка. Але саме Японія подарувала світу мистецтво орігамі.

Розквіт мистецтва орігамі припадає на середину двадцятого століття, робочий-металіст Акіра Йошизава вирішив присвятити себе орігамі та його розвитку. Основна заслуга А. Йошизава в тому, що він зумів створити те, що сьогодні називають «Азбукою орігамі». Умовні позначення, символи, графічні знаки, які придумав А. Йошизава, дозволили зафіксувати на папері процес складання фігур орігамі. Це відкриття дозволило орігамі стати універсальною, міжнародною мовою.

В сорокових роках створюються перші Центри і школи орігамі. Перший Центр Орігамі створила орігамістка Ліліан Оппенгеймер в Нью-Йорку.

Сьогодні мистецтво орігамі відкрито всьому світу. Заняття орігамі дозволяє людині хоч не надовго відірватися від повсякденних проблем і полетіти разом з квадратним аркушем паперу в прекрасну країну Мистецтва.

 

2.1.3. Легенди про орігамі

Легенда про тисячу журавликів

Найголовніша японська легенда пов'язана з образом журавлика. Всі знають, що в країнах Сходу його вважають символом щастя, дружби та любові. Люди вірять, що коли зробити тисячу фігурок цієї пташки, а потім подарувати їх своїм друзям, то обов'язково здійсниться найзаповітніша мрія.

Якщо вірити легенді, то колись жив один майстер. Він був дуже бідний, але водночас дуже добрий. Цілими днями майстер складав з паперу різні фігурки і роздавав їх дітям. А одного разу він подарував свій виріб монахові, який брів дорогою. Це була фігурка журавлика. Мудрий монах сказав йому: «Твоє мистецтво зробить тебе багатим. Складай свої фігурки й надалі, але пам'ятай: коли складаєш, потрібно не думати про все навколишнє. Навіть якщо навколо тебе йде війна, ніщо не повинно відволікати твою увагу». Майстер послухав мудрого монаха і продовжував працювати.

Невдовзі, дійсно, почалася війна. Молоді пішли воювати, а старим доручили наглядати за дітьми та жінками. Настали важкі часи. Люди втрачали віру та надію на краще. Вони не розуміли нашого майстра, який не дивлячись ні на що, не залишав свої заняття. Розізлившись, вони вирішили спалити майстерню, але коли вони зайшли до майстерні, їх вразила різноманітність та неймовірна краса фігурок. Майстер запропонував вибрати кожному по одній. Люди почали запитувати, чому він їх виготовляє. І майстер сказав: «Я вірю, що вони дарують щастя». На очах у всіх він склав з паперового аркуша журавлика. І раптом птах змахнув крилами і, зірвавшись з руки, вилетів у вікно. Люди знову повірили в себе і змогли не тільки подолати ворога, але й відновити зруйноване селище.

Це лише одна з багатьох легенд. Насправді їх є тисячі, і кожен народ вірить в свою. На основі однієї легенди виникло ще кілька.

Після другої світової війни у відомої фігурки журавлика з'явилося нове значення. Його почали називати символом миру. Цьому також передує одна легенда. До цих пір кругом дітям розповідають про японську дівчинку на ім'я Садако Сасакі. Вона народилась в 1943 році. Батьки дівчинки загинули під час атомного бомбардування Хіросіми, а сама вона захворіла на променеву хворобу. Дівчинку забрали до шпиталю, а там вона почала складати паперових журавликів.

Дівчинка вірила, що історія про тисячу журавликів не вигадка, і бажання здійснюються. Мріючи про видужання, вона складала журавликів, також просячи в думках про мир на планеті. Нажаль, закінчити роботу вона не змогла. Вона померла 25 жовтня 1955 року, виготовивши тільки 644 журавлика. Цю надію дівчинки підхопили інші люди і теж почали виготовляти цих птахів, відсилаючи їх в музей миру. Так журавлик став символом миру.

Легенда про кулю орігамі (кусудама)

За іншою легендою, орігамі має властивість зберігати частинку душі господаря. Вважають, що, складаючи фігурку, майстер вкладає в неї частинку самого себе. А тому разом з господарем помирає і його орігамі. Японці розповідають, що колись одній дуже впливовій людині за надану послугу було подаровану кулю орігамі. Не знайшовши їй належне призначення, багатій віддав кулю своїй пристарілій матері, яка проживала окремо. Мати повісила кулю в кімнаті над столом. Несподівано багатій захворів. Мати дуже хвилювалася, але зла невістка не впускала її до оселі і нічого не розповідала. Скоро син помер. Коли до жінки прийшли, щоб повідомити цю новину, вона вже все знала. Виявилось, що в ту мить, коли її син помер, куля впала і розлетілась на частинки.

Створюючи орігамі, не можна думати про погане. Жителі Сходу впевнені, що якщо, створюючи орігамі, майстер думав про погане, а потім не спалив свій виріб, а подарував другові, той може захворіти. В свою чергу, захворіє й майстер, якщо його подарунок буде знищено. Тому орігамісти обов'язково просять зберігати подаровану фігурку як талісман і рідко дарують вироби незнайомим людям.

В зв'язку з тим, що в Японії до цих пір вважають орігамі талісманом вдачі та успіху, деякі фірми використовують його в якості торгової марки. Одна із таких марок відома всьому світу, це значок «Міцубісі». Зображення на ньому трьох трикутників, це не що інше, як фігури орігамі.

Варто тільки повірити в силу талісману, і подарунок починає приносити вам приємні сюрпризи. Один з таких сюрпризів описаний в легенді.

Легенда про паперовий нарцис

Один бідний юнак закохався в багату дівчину. Але у нього не було грошей, щоб робити їй дорогі подарунки, а тому він кожного дня приносив і ставив їй на підвіконня букет живих квітів. Коли прийшла зима і квіти зів'яли, він почав виготовляти паперові квіти. Виготовляючи їх він вкладав своє кохання і ніжність. Але дівчина була капризною і ніколи не брала тих квітів. Їх викидала її покоївка.

Та одного разу, коли покоївка забула це зробити, кохана юнака таки взяла квітку в руки і несподівано відчула, що вона насправді має дуже приємний запах. Це був прекрасний паперовий нарцис. Вона не могла повірити в це чудо. Їй здавалося, що цей аромат приніс вітер. І тоді вона поставила квітку до скриньки. Діставши її на слідуючий день, була вражена: запах не зник. Тоді дівчина зрозуміла, наскільки справжнє кохання юнака, і закохалася теж.

Відомі випадки, коли папір намагались використовувати для лікування, і про це також складали легенди.

Легенда про магічний знак

Колись давно говорили, що в одному з давніх селищ вибухнула епідемія холери. Люди помирали і ніхто не міг допомогти. Одного разу біля селища проходили двоє подорожуючих: вчитель та його учень. Дізнавшись про біду, вони вирішили допомогти жителям. Деякий час вони готувалися, а потім наказали селянам в одному порожньому будинку, принести туди навіть тих, хто був уже невзмозі ходити, і добре закрити вікна. Як тільки це було зроблено, вчитель сів посередині будинку в позі лотоса, накреслив на паперовому аркуші якийсь магічний знак, поклав аркуш перед собою і почав медитувати.

Учень майстра запалив вогнище з хмизу та соломи. Коли вогонь повністю розгорівся, майстер спалив на ньому аркуш з накресленим на ньому магічним знаком. Дим, який утворився, розійшовся по будинку, почав душити людей. Хворі кашляли, стогнали, деякі, навіть, блювали. Цим димом накрив все селище, читаючи при цьому таємні заклинання. Коли дим розсіявся, люди відчули покращення.

Один з сучасних парапсихологів вирішив виміряти біоенергетику паперових виробів. Він був вражений. Виявилось, що в приміщенні, де є фігурки орігамі, енергетика в багато разів вища, ніж без них.

 

2.1.4. Види і техніки орігамі

Розрізняють такі види та техніки орігамі:

1. Модульне орігамі

Однією з популярних різновидів орігамі є модульне орігамі, в якому ціла фігура збирається з багатьох однакових частин (модулів). Кожен модуль складається за правилами класичного орігамі з одного аркуша паперу, а потім модулі з'єднуються шляхом вкладання їх один в одного, що з'являється при цьому сила тертя не дає конструкції розпастися. Одним із відомих об'єктів модульного орігамі є кусудама, об'ємне тіло кулястої форми.

2. Просте орігамі

Просте орігамі - стиль орігамі, придуманий британським орігамістом Джоном Смітом, і який обмежений використанням тільки складок горою і долиною. Метою орігамі є полегшення занять недосвідченим орігамістам, а також людям з обмеженими руховими навичками. Дане вище обмеження означає неможливість багатьох (але не всіх) складних прийомів, звичних для звичайного орігамі.

3. Складання по розгортці

Розгортка (англ. Creasepattern; патерн складок) - один з видів діаграм орігамі, який представляє собою креслення, на якому зображені всі складки готової моделі. Складання по розгортці складніше складання за традиційною схемою. Проте, даний метод дає не просто інформацію, як скласти модель, але і як вона була придумана. Справа в тому, що розгортка використовується при розробці нових моделей орігамі. Останнє також робить очевидним факт відсутності для деяких моделей інших діаграм, крім розгортки.

4. Мокре складання

Мокре складання - техніка складання, розроблена Акірою Йошидзавой. Вона використовує змочений водою папір для додавання фігуркам плавності ліній, виразності, а також жорсткості. Особливо актуальний цей метод для таких негеометричних об'єктів як фігурки тварин і квітів - в цьому випадку вони виглядають набагато природніше і ближче до оригіналу.

Не всякий папір підходить для мокрого складання, а лише той, в який при виробництві додають водорозчинний клей для скріплення волокон. Як правило, даними властивостями володіють щільні сорти паперу.

Класичні фігури орігамі можна відшукати у мережі Інтернет за адресою:

http://www.origami.ru/mod/i_clas.htm

Учні виготовляли моделі фігур - орігамі за схемами:

Орігамі - стаканчик

(одна з найпростіших фігур-орігамі)

 

 

 

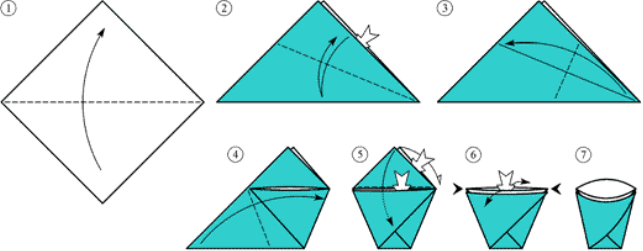
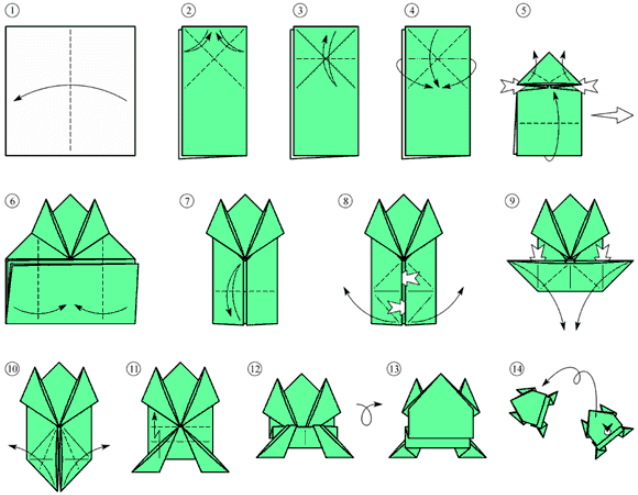
Класична модель жабки

 

 

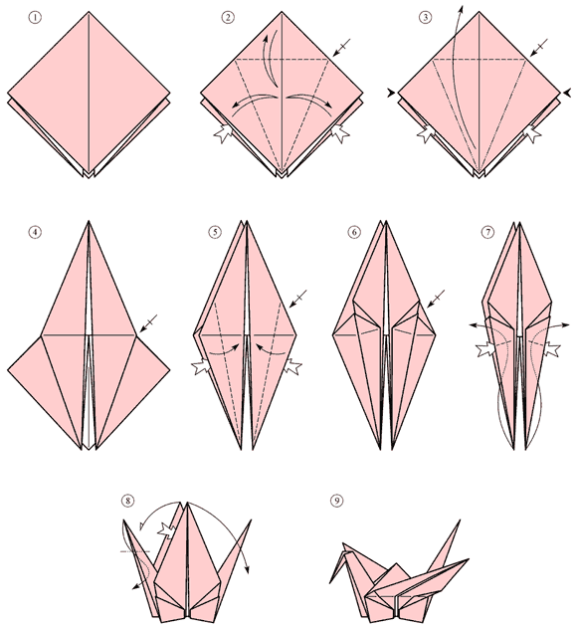
Класичний журавель

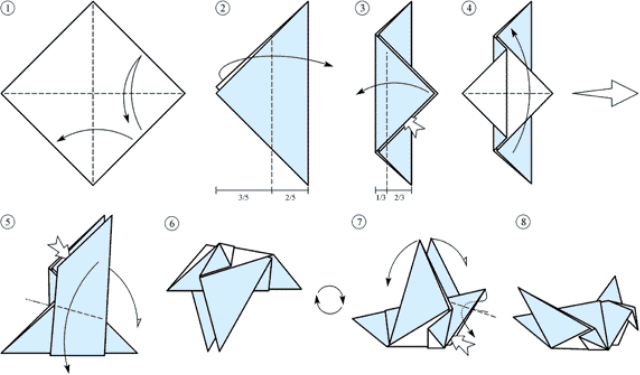
Голуб

 

 

 

Тюльпан (https://www.youtube.com/watch?v=qpi_JbOJUIw&feature=youtu.be)

Модульні орігамі

Квіткова кусудама - традиційна японська кусудама

Дана кусудама робиться з використанням клею . Спочатку склеюються пелюстки квітки між собою, а потім - самі квіти у квіткову кулю. Щоб виготовити кулю, потрібно дванадцять таких квіток.

Схеми складання можна відшукати за адресами в мережі Інтернет:

http://www.business-lady.com/ideya_narod_150.php

http://poradu.pp.ua/svoyimi-rukami/13495-kusudama-dlya-pochatkvcv-orignaln-prikrasi-svoyimi-rukami.html

 

 

Лебідь з модулів орігамі

Як зробити модуль орігамі? Майстер-клас для початківців можна переглянути на відеохостингу YouTube: https://www.youtube.com/watch?v=ZMzh59YtJT4.

Скласти лебедя з модулів орігамі допоможе перегляд відео: https://www.youtube.com/watch?v=K7nJuCxttjA

https://www.youtube.com/watch?v=zqB9F-llgeU

Творимо красу, вона рятує світ від сірості і посередності!

 

Виставка творчих робіт

Учні виготовляють модулі орігамі для складання лебедя

Презентація модульних орігамі: лебідь, кусудама, ваза

2.1.5. Орігаметрія як нова математична теорія

Математики давно переконалися, що за допомогою різних способів орігамі можна розв'язати найскладніші задачі. Науковці об'єднали методи орігамі з геометрією і назвали нову гілку мистецтва орігаметрією.

Орігаметрія – це зовсім інший, оригінальний підхід до розв'язування геометричних задач.

В основу орігаметрії покладено твердження:

1. Роль прямих будуть виконувати краї аркуша та лінії перегину, що утворюються при його складанні.

2. Роль точок - вершини кутів аркуша і точки перетинів ліній згину один з одним або з краями аркуша.

3. Основні поняття орігаметрії: точка, лінія згину, квадратний аркуш паперу.

4. Основні відношення: лінія згину проходить через точку; точка належить лінії згину.

Орігаметрія досить молода математична теорія. Як і будь-яка теорія, орігаметрія має свою систему аксіом.

Видатний італійський математик із японським походженням Хуміакі Хузіта (Humiaki Huzita), разом зі славетним японським майстром орігамі Акіро Йошидзава сформулювали систему аксіом(шість аксіом).

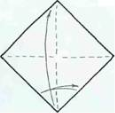
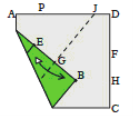
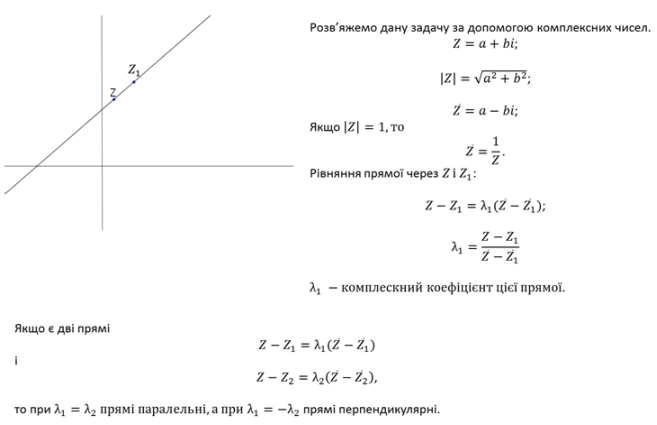
Аксіома A1. Існує єдиний перегин p, який проходить через дві подані точки A і B (рис.2.1)

.

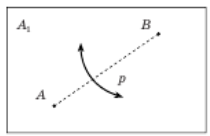
Рис.2.1 Аксіома А1

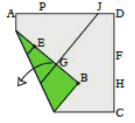
Аксіома A2. Існує єдиний перегин p , який суміщає дві подані точки A і B (рис. 2.2).

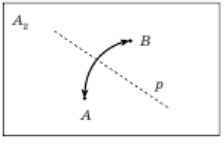
Рис.2.2 Аксіома А2

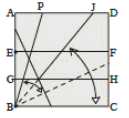
Аксіома A3. Існує перегин p , який суміщає дві подані прямі a і b (рис. 2.3).

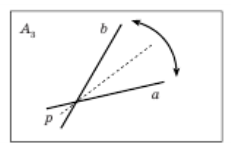
Рис.2.3 Аксіома А3

Аксіома A4. Існує єдиний перегин p , який проходить через подану точку A і є перпендикулярним до поданої прямої a (рис. 2.4).

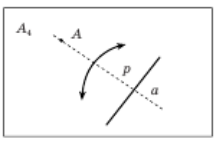
Рис.2.4 Аксіома А4

Аксіома A5. Існує перегин p , який проходить через подану точку A і зміщує іншу подану точку B на подану пряму a (рис. 2.5).

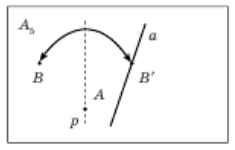
Рис.2.5 Аксіома А5

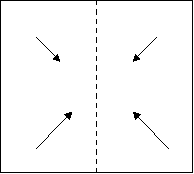
Аксіома A6. Існує перегин, який зміщує кожну з двох поданих точок A і B на одну з двох поданих прямих a і b, які перетинаються (рис. 2.6).

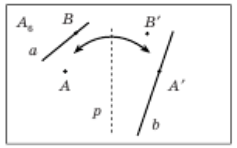
Рис.2.6 Аксіома А6

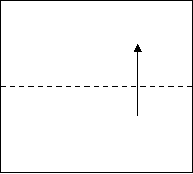
Аксіома А7 Існує перегин, який зміщує дану точку на пряму і є перпендикулярним до іншої прямої (рис.2.7).

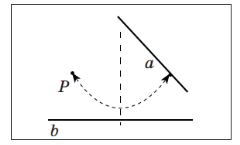
Рис. 2.7 Аксіома А7

Система аксіом A1 - A5 − еквівалентна системі аксіом геометрії, де в якості основного інструмента виступає креслярський трикутник.

Звідси випливає, що методами орігамі, тобто лише перегинами аркуша паперу, можна розв’язати будь-які задачі на побудову, які можна розв’язати класичними інструментами – циркулем і лінійкою. Шоста аксіома не може бути проілюстрована  методами конструктивної геометрії, оскільки обґрунтування побудов, які проводяться в цій аксіомі, зводяться до розв’язування кубічного рівняння, яке не має раціональних коренів.

Сьома аксіома з’явилася пізніше. Вона була відкрита Кошіро Хаторі. Американський математик Роберт Ленг довів, що подана аксіома завершує список аксіом орігамі. Тобто дана система аксіом є повною.

Розв’язання будь – якої задачі орігаметрії складається із:

1.               Постановка задачі. Аналіз умови, виокремлення даних компонентів, дослідження їхніх властивостей.
2.               Розв’язання за допомогою орігамі. Перевірка виконання заданої умови або побудова шуканої фігури.
3.               Математичне обґрунтування. Доведення того, що в результаті дійсно отримано фігуру з шуканими властивостями.

Існує багато типів задач, до яких можна застосувати метод перегинів. Серед них задачі на побудову, на доведення, задачці на знаходження розмірів шуканих фігур, на знаходження площі, периметра фігур тощо.

 

6. Розв’язування геометричних задач методом перегинів

Розглянемо кілька задач, від найпростіших до більш складних, щоб проілюструвати красу і можливості зазначеного методу.

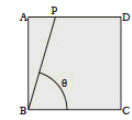
Задача 1. Придумайте, як із листа прямокутної форми виготовити лист квадратної форми?

Учні запропонували два способи розв’язання:

         

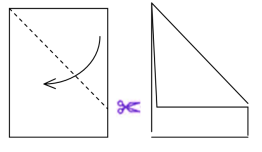
    Рис. 2.8 1-й спосіб   Рис. 2.9 2-й спосіб

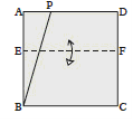
Задача 2. Візьміть квадратний аркуш паперу, який би був з одного боку білий, а з іншого – блакитний (кольоровий). Які блакитні многокутники можна отримати, загинаючи один кінець цього квадрата, якщо квадрат розташовано білим кольором до нас?

Розв’язання

Можна отримати трикутники, чотирикутники, п’ятикутники. А ось уже шестикутник отримати не можна.

Влаштуйте обговорення: чому саме такі n – кутники отримали? Можна продовжити дослідження і запропонувати учням аналогічне завдання, але з вихідною фігурою трикутник (п’ятикутник, шестикутник). Кожного разу ми зможемо отримувати фігури від трикутника до n+1 – кутника, де n – кількість кутів вихідного многокутника.

Задача 3. Без креслярських інструментів поділити квадрат на 2, 4, 3, 6 частин.

На дві та чотири частини поділити квадрат досить легко: потрібно лише скласти навпіл квадрат один раз – поділ навпіл, ще раз – поділ на чотири частини. Поділ квадрата на три частини дещо складніша задача. Розв’язок її зображено на рис.2.10.

Рис.2.10

Задача 4. Поділити даний відрізок у відношенні 2 до 3.

Розв’язання

Взяти квадратний аркуш і виконати необхідні перегини: спочатку виконати перегин аркуша навпіл, а потім уздовж лінії ВС. Точка А перейде у точку Р. Тепер виконати перегин, що проходить через точку Р і переводить пряму АВ у себе (тобто перегин буде перпендикулярним до АВ), отримаємо точку Н. АН:НВ=2:3.

Рис.2.11

Задача 5. Поділити прямий кут на кути .

Для розв’язування задачі візьмемо квадрат. Спочатку поділимо квадрат на два рівні прямокутники. Отримаємо лінію поділу. Перегнемо квадрат так, щоб одна із його вершин лягла на утворену лінію. Отриманий кут дорівнює . Інший кут рівний . Поділивши кути навпіл, отримаємо кути відповідно (Рис. 2.12)

Рис.2.12

Доведення

Рис 2.13

Використовуючи схему (рис 2.13), маємо:

АВ=АС=ВС і ∆ВАС – рівносторонній, отже АВС=60⁰.

ОВА=90⁰-60⁰=30⁰, ABN=30⁰,  ОВА= ABN= NBC=30⁰.

Розв’язуючи дану задачу, ми поділили прямий кут на три рівні частини.

Використовуючи задачу 4 нескладно розв’язати задачі на побудову рівностороннього трикутника в квадраті.

Задача 6. Із квадрата утворити правильні многокутники:

              

Рис 2.14

1.               Рівносторонній трикутник.

Схема розв’язання задачі зображено на рис. 2.15.

Рис. 2.15

Можна запропонувати також інший спосіб побудови правильного трикутника (рис. 2.16).

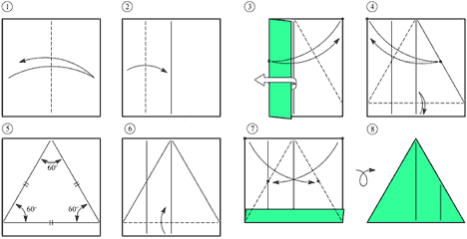
Рис. 2.16

2.               Правильний п’ятикутник (рис. 2.17):

Рис. 2.17

3.               Правильний восьмикутник (рис. 2.18):

Рис. 2.18

4.               Побудувати правильний шестикутник (рис. 2.19).

Побудова

1.               Намітити на квадраті вертикаль і перегнути його навпіл в трикутник.
2.               Намітити середину правої сторони.
3.               Намітити верхню четвертинку правої сторони.
4.               Перегнути правий кут так, щоб лінія перегину пішла із середини основи і вказані точки співпали.
5.               Перегнути ліву частину назад.
6.               Відрізати верхню частину (лінія розрізу йде від кута до кута) і розгорнути нижню.

 

 

   

 

         а)                         б)                                в)                             г)

 

 

 

 

          д)                           є)                                 ж)                           з)

Рис. 2.19

Задача 7. Знайти кут між бісектрисами суміжних кутів.

Дана задача може формулюватись дещо по іншому. Довести, що кут між бісектрисами суміжних кутів дорівнює

Ці задачі розв’язуються за одним алгоритмом (Рис. 2.20а, 2.20б)

   

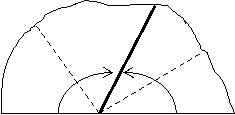
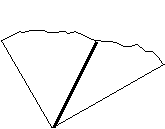
          Рис. 2.20а                                               рис. 2.20б

В результаті перетворень розгорнутий кут () перетворився на два рівних кути. Тому градусна міра кожного з них дорівнює .

Задача 8. На малюнку зображено трапецію (рис. 2.21) А, В – середини її бічних сторін. Якщо площа сірого прямокутника 13см², то площа трапеції рівна…

Рис. 2.21

Щоб розв’язати дану задачу, необхідно перегнути трапецію по лініях прямокутника. Отримаємо два рівних прямокутники із площею 13см². Отже, площа трапеції рівна 26см².

Задача 9. Із заданого квадрата отримайте квадрат, площа якого у 2рази менша від вихідного (2.22).

 

 

 

 

 

 

Рис. 2.22

Виведення формул площ

Одна з найдавніших практичних задач – визначення площ геометричних фігур. Ця задача і сьогодні залишається такою ж актуальною. Одним із способів знаходження площ фігур – є використання формул. Способів доведення формул є досить багато. Також можна використати спосіб орігамі.

У класичному орігамі використовуються квадрати. В сучасному – можна використовувати й інші фігури.

1.               Виведемо формулу площі трикутника 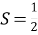  ah

Доведення

Нехай дано трикутник з стороною a та висотою h. Спочатку відшукаємо точку основи висоти. Для цього перегнемо трикутник так, щоб пряма перегину пройшла через вершину трикутника, що лежить навпроти даної сторони.

Перегнемо трикутник так, щоб всі вершини збігалися з точкою основи висоти.

Після виконаних перегинів, ми отримаємо два прямокутники зі сторонами .  Обчислимо площу утвореного прямокутника:

.

Оскільки заданий трикутник перетворився на два прямокутники, площу одного з яких ми знайшли, то площа трикутника:

 .

2.               Доведемо формулу для обчислення площі прямокутного трикутника зі сторонами a і b.

Алгоритм подібний до попереднього. Перегнемо дві вершини трикутника до вершини прямого кута. Отримаємо прямокутник зі сторонами . Таких прямокутників утвориться два, тому площа трикутника:

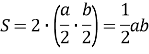
3.               Формула обчислення площі ромба   ,

де - діагоналі ромба.

Спочатку знайдемо точку перетину діагоналей ромба – перегнемо ромб навпіл (двічі). Потім перегнемо всі вершини фігури до точки перетину діагоналей. В результаті отримаємо два прямокутники зі сторонами та  . Звідси площа ромба:   .

Аналогічно доводиться формула площі квадрата.

4.               Формула для обчислення площі паралелограма  , де  a – сторона паралелограма, h – висота паралелограма, проведена до даної сторони.

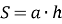
Спочатку перегнемо фігуру так, щоб сторони паралелограма лежали на одній прямій (вибираємо сторони, що розташовані горизонтально). Перегнемо гострі кути паралелограма (один на лицеву сторону, інший – на зворотну) так, щоб утворився прямокутник зі сторонами .  Звідси площа паралелограма:  

5.               Досить цікаво доводиться формула площі трапеції з основами a і b та висотою h.

Насамперед перегинаємо трапецію так, щоб основи лягли одна на одну. Гострі кути перегинаються на лицевий бік. Утвориться прямокутник зі сторонами

Звідси:    .

Доведення теорем

Теорема 1. Сума кутів трикутника дорівнює 180 градусів.

Доведення

1. Взяти аркуш паперу, що має форму довільного трикутника.

2. Проведемо перегин через одну з вершин трикутника, перпендикулярно протилежному боку ( висоту трикутника) .

3. Сумістимо вершини трикутника з точкою біля основи висоти трикутника.

4. Отримаємо, що кути 1, 2, 3 трикутника збіглися при накладенні з розгорнутим кутом. Отже, сума кутів дорівнює 180 градусів.

 

 

 

 

 

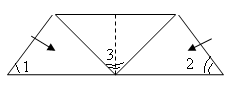
Рис. 2.23

Теорема 2. Вертикальні кути рівні.

Доведення

1. Перегнемо аркуш паперу двічі так, щоб утворилося дві прямі, що перетинаються.

2. «Заховаємо» два зайві кути. Отримаємо рівні вертикальні кути.

Теорема 3. Внутрішні різносторонні кути при паралельних прямих, перетнутих січною, рівні.

Доведення

1. Візьмемо аркуш паперу з двома паралельними сторонами. Проведемо січну і відмітимо внутрішньо різносторонні кути.

2. Сумістимо вершини січної. Відмічені наші кути накладаються.

Отже, внутрішні різносторонні кути рівні.

 

Розв’язання нерозв’язних за допомогою циркуля і лінійки задач методом орігамі

Ще в античності були поставлені такі три задачі на побудову:

•                   Трисекція кута – розбити довільний кут на три рівні частини.
•                   Подвоєння куба – побудувати відрізок, що є ребром куба вдвічі більшого об'єму, ніж куб з даним ребром.
•                   Квадратура круга – побудувати квадрат, рівний за площею даному кругу.

У XIX столітті було доведено, що всі три задачі нерозв'язні циркулем та лінійкою.

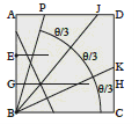
Задача. Поділити кут на три рівні частини.

Дану задачу можна розв’язати методом орігамі. Це розв’язання запропонував Хісасі Абе.

Розв’язання

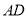1. Взяти аркуш паперу квадратної форми і позначити його як . На стороні позначити довільну точку Р і провести відрізок 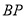. Потрібно розділити кут 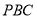на три рівні кути (рис. 2.24а).
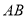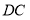2. На сторонах і позначити точки 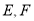так, щоб лінія 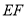була паралельною 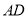. Позначити 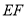за допомогою перегину. (рис. 2.24б)
3. Сумістити сторону 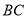з лінією 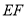. Лінію, отриману в результаті перегину, позначити як 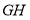(рис. 2.24в)
4. Зробити такий перегин, щоб точка Е дотикалася лінії 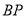і точка 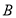дотикалась лінії 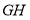(рис. 2.24г).
5. Перегнути аркуш по перпендикуляру до лінії 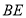, що проходить через точку . На стороні позначаємо точку (рис. 2.24д).
6. Відгинаємо кут назад (рис. 2.24е).
7. Довести лінію, що виходить з точки до точки . Сторону 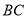сумістити з лінією 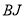(рис. 2.24є).
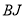8. Лінії і 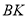ділять кут на три рівні частини (рис. 2.24ж)

 

 

 

 

 

 

 а)                            б)                           в)                           г)

 

 

   

 

           д)                           е)                                є)                           ж)

Рис. 2.24

У задачі ми розглянули випадок коли заданий кут – гострий. У побудові трисекції тупого кута можна скористатись наступним підходом: побудувати трисекцію суміжного гострого, а потім від крайньої побудованої трисектриси відкласти кут 60°. Переконаємося у правильності побудови. Нехай тупий кут дорівнює 3β, а суміжний гострий - 3α, тоді 3α+3β=180°, а α+β=60°.

Цією задачею список «неможливих побудов» не обмежується. За допомогою перегинів можна також побудувати правильний семикутник, який не можливо побудувати, використовуючи тільки циркуль та лінійку, а також розв’язати стародавню задачу «подвоєння куба».

Існує ще багато задач де можна застосувати метод орігаметрії. Причому ці задачі є наочними та ілюструють доступність пояснення ходу думок.

 

2.1.7. Застосування орігамі в науці і житті

Повідомлення учня.

Для мене стало відкриттям, що орігамі знайшло застосування і в інших науках, а також широко використовується в сучасних технологіях. Наприклад, в 1970 році японським астрофізиком Коріо Міура на основі техніки жорсткого орігамі була розроблена схема складання «Міура-орі», яка використовується сьогодні для розгортання установок сонячних батарей на космічних супутниках. Спочатку ця технологія використовувалася для складання паперових документів, карт місцевості, упаковок. Наприклад, при складанні карт складки Міура-орі розташовані не під прямими кутами, а злегка нахилені по відношенню один до одного.В результаті така карта компактна, в складеному вигляді являє плоску фігуру, але її можна розгорнути і згорнути одним рухом , а відсутність багатошарових складок зменшує навантаження на папір. Це хороший приклад практичної важливості жорсткого орігамі, що розглядає складки як петлі, що з'єднують дві плоскі, абсолютно тверді поверхні.

За допомогою основ орігамі інженери навчилися конструювати абсолютно нові технічні машини, телескопи для космічних кораблів. Багато часу та сил було затрачено для виготовлення телескопу з великою лінзою. Довго не могли помістити лінзу необхідного розміру у вузький «Шатл». І тоді за допомогою «обчислювального орігамі» науковці змогли краще зрозуміти, як об'єкти реагують на різні ступені тиску. В результаті це дало змогу скласти велику лінзу так, щоб її горизонтальні розміри зменшились і вона пройшла в «Шатл», де потім була розвернута.

У процесі вивчення орігамі я дізнався, що воно позитивно впливає на роботу головного мозку. Професор Кавасима Рюта займається вивчення фізіології мозку в Інституті вікової медицини при університеті Тохоку. Він показав, що виконання орігамі збільшує потік крові, що проходить через префронтальну зону головного мозку, допомагаючи йому краще працювати.

2.2. Проект «Літо інтелекту - відпочинок з математикою»(10 класи)

Орієнтовний план проекту

Понеділок   

І. Знайомство учнів в команді.

1. Тренінг «Хто Я? Який Я?»

ІІ. Поділ на групи. Назви груп.

2. Визначення правил роботи. Розподіл обов’язків.

3. Турнірний рух в Україні. Як навчитись перемагати в турнірах.

     Зустріч з психологом.

Вівторок    

І. Змістовне  насичення до проекту.

1. З чого починається турнір.Секрети турнірних задач.

2. Прості і складені числа. Обговорення задачі «Складене число» з ХVIII Всеукраїнського турніру юних математиків.

3. Дискусія з теми «Діаметрально протилежні точки».

Середа    

І. Практичне насичення проекту.

1. Наукова дискусія «Тригонометричні функції».

2. Задачі на побудову. Відновлюємо трикутник лише циркулем та лінійкою.

3. Від простого до складного. Коло ідей.

Четвер     

І. Створення проекту.

1. Елементи турнірної стратегії.

2. Презентація задачі «Композиція тригонометричних функцій».

3. Особливості ролі Доповідача, Опонента та Рецензента в турнірній грі.

 

П’ятниця     

І. Гімназія + ВНЗ.

1. Співпраця з вченими: рекомендації з розв’язування турнірних задач.

2. Дослідницький клубок однієї задачі.

3. Зустріч з викладачем СНУ імені Лесі Українки Філозофом Л.І., кандидатом фізико-математичних наук.

Понеділок   

1. Розв’язування алгебраїчних завдань ЗНО.

2. Розв’язування геометричних завдань ЗНО. Коло ідей.

Вівторок    

1. Полеміка, дебати, коло ідей до задач турніру.

2. Дискусія з теми «Нелінійна система рівнянь».

3. Цікава задача  «Країна чотирьох островів»

 Середа    

1. Обговорення задачі ЗНО на дослідження коренів раціонального рівняння з параметром, яке містить тригонометричну функцію (поглиблений рівень).

2. Презентація задачі «Нелінійна система рівнянь».

Четвер 

1. Ми з насолодою пізнаємо математику. Світ цікавих ігрових задач.

2. Задача  «Перестановка чисел». Коло ідей до задачі турніру.

3. Презентація задачі  «Країна чотирьох островів».                                                    

 

П’ятниця

І. Презентація проекту.

1. Презентація та захист турнірних задач.

2. Полеміка, дебати.

3. Підведення підсумків.

ІІ. Нагородження.

 

Навчальний проект «Літо інтелекту - відпочинок з математикою» запропонований для учнів 10-х класів.

Мета: вдосконалення вмінь і навичок розв’язування нестандартних задач (задач ЗНО та турнірних задач), розвиток науково-дослідницького підходу до розв’язування задач, формування в учнів інтересу до прикладної математики, забезпечення інтелектуального зростання учнів, створення умов, необхідних для розвитку індивідуальності учнів.

Завдання проекту: ознайомити учнів з турнірним рухом в Україні, специфікою турнірної задачі; формувати вміння учнів вести наукову дискусію в ролях (доповідач, опонент, рецензент), створювати презентації до виконаних досліджень.

Обладнання: мультимедійний проектор, телевізор, комп'ютери.

Методичні матеріали:

• Презентація вчителя
• Джерела інформації

Ключове питання:

Як навчитись перемагати в турнірах.

Діяльність учнів

Учні познайомилися зі стартовою презентацією, обговорили ключове та тематичні питання, вибрали напрямки для досліджень, ознайомилися зі списком джерел інформації.

За напрямком дослідження: з чого починається турнір?

• Познайомилися з історією турнірного руху в Україні
• Підібрали задачі з вiдбiркових етапiв турнiру
• Відшукали в мережі Інтернет задачі ХVIII всеукраїнського турніру юних математиків імені професора М.Й.Ядренка        
• Опрацювали вибрані задачі (дослідили) та зробили необхідні висновки  (розв’язали).
• Оформили результати досліджень у вигляді презентації

За напрямком дослідження: турнір – це особлива рольова гра

• Розподіл ролей Доповідача, Опонента та Рецензента
• Дискусії з вибраних тем (математичний бій)  
  • Презентація турнірних задач.

 

2.2.1. Турнірна задача як елемент спільної дослідницької діяльності науковців, учителів та учнів

Повноцінними є тільки ті знання,

які дитина здобула власною активністю.

Йоганн Песталоцці

Науково-дослідницька діяльність у школі – це творча праця учня під керівництвом учителя, яка полягає у відкритті нових знань на основі науки та особистого досвіду дитини. Дослідницька діяльність – потужний засіб розвитку компетентності дитини, ефективна форма пізнання та самоосвіти учня.

Турнір, як форма роботи з обдарованою молоддю, відрізняється особливістю, як за формою проведення, так і за своєю суттю. Саму форму підготовки і проведення турнірів важко переоцінити в плані виховання і розвитку математичних здібностей обдарованих учнів. Але є ще один аспект турнірних задач, який, можливо, на сьогодні ще не оцінено в повній мірі. Це пов’язано з тим, що майже кожна турнірна задача передбачає не тільки її узагальнення, але і можливість розвитку ідеї, закладеної в задачу, та, навіть, генерацію нових ідей.

Головна мета турніру – створення умов для реалізації та розвитку творчих здібностей школярів, формування в учнів інтересу до прикладної математики, пошук школярів, схильних до наукової діяльності та здатних, застосовуючи знання з математики, знаходити оригінальні технічні рішення.

Турнір юних математиків є командним змаганням учнів в їх спроможності вирішувати складні математичні проблемні завдання, представляти рішення в переконливій формі та захищати їх в науковій дискусії

Турнір юних математиків проводиться в три етапи:

•          І етап – заочний;
•          ІІ етап – регіональний очний (міський, обласний);
•          ІІІ етап – Всеукраїнський очний.

На І етапі (заочному) в школах створюються творчі учнівські колективи, до роботи яких потрібно долучати учителів, студентів, науковців, які працюють над розв’язанням подібних задач. Така співпраця дає змогу школярам успішно проводити науковий пошук, дає можливість самостійно ознайомитися з математичною літературою, принциповими математичними фактами, набути навичок колективної творчої праці.

Одержавши відповідний комплект задач, необхідно ознайомити з ним якомога ширше коло учнів, відобразивши ідею турніру, зацікавити та захопити учнів. Учитель, проаналізувавши зміст і рівень задач, можливі напрямки дослідження, збирає всіх охочих випробувати свої сили в розв’язуванні запропонованих завдань.

Ознайомивши учнів на першій зустрічі зі специфікою турніру, доцільно підкреслити дослідницький характер задач, зосередити їх увагу на власне бачення запропонованої моделі, можливих напрямів дослідження, ігровий дискусійний характер презентації та захисту своїх напрацювань. Далі необхідно детально розібрати завдання з метою розуміння їх умов учнями, надати методичні рекомендації щодо теоретичного опрацювання необхідного матеріалу.

 

Дискусія з теми «Нелінійна система рівнянь»

Готуючись до змагань, учасники опиняються у тих же  умовах, у яких знаходяться зазвичай дослідники. Ні розв’язок задачі,  ні хід розв’язування заздалегідь не відомі. Від учасників вимагається здобути необхідну інформацію (набути знання), опрацювати її (дослідити) та зробити необхідні висновки  (розв’язати). При цьому вміння організувати діяльність, навички роботи в команді відіграють дуже важливу роль. Для успішного виступу на турнірі також дуже важливим є ще один вид діяльності – вміння презентувати зроблене. Членам команди потрібно підготувати структуровану доповідь у якій переконливо викласти всю необхідну інформацію та результати дослідження напрацьовані у процесі розв’язання конкретної задачі.

Значення турнірного руху з точки зору його впливу на інтелектуальне становлення молодої особистості важко переоцінити, оскільки розвиток здібностей обдарованої молодої людини,  рівень інтелектуального розвитку,  коло навчальних, а згодом наукових інтересів визначається середовищем спілкування, рівнем завдань,  які людина ставить перед собою та можливостями досягнення поставлених цілей. Жодна з інших форм роботи з обдарованою молоддю практично зовсім не передбачає колективну працю щодо здобуття знань, пошуку шляхів вирішення наукової (навчальної) проблеми, дослідження певного явища,  процесу тощо. Підготовка та участь у турнірах передбачає, як обов’язковий компонент, спілкування з однолітками, педагогами, науковцями, виробничниками. Обдаровані учні вчаться самостійно планувати свою роботу, розподіляти напрямки діяльності, обмінюватися думками, дискутувати, приймати спільні рішення щодо поставлених проблем. Фактично учні саморозвиваються, самовдосконалюються, набуваючи відповідні знання, вміння та навички здобуття нових знань та співпраці у процесі дослідження та розв’язання проблеми.

Особлива складність полягає в тому, що для розв’язування турнірних задач потрібний науково-дослідницький підхід, який передбачає застосування програми поглибленого вивчення математики, використання багатьох спеціальних тем. Наукою математикою займаються, як показує досвід, ті учні, які мають достатні здібності та сильну внутрішню мотивацію, тобто по справжньому захоплені серйозною академічною математикою, проявляють інтерес до дослідницької роботи.

Обговорення задачі 35 ЗНО 2015року

 

Турнір юних математиків є спільною діяльністю учнів, вчителів, науковців на всіх етапах освітнього процесу з широким застосуванням активних та інтерактивних технологій навчання, що забезпечують максимальну самостійність та активність усіх учасників процесу навчання.

Турнір – це особлива рольова гра, що відбувається у формі наукової дискусії. Тому пропонуємо методичні поради  для організації роботи по підготовці до турнірів з власного досвіду.

 

2.2.2. Як правильно розподілити ролі в турнірній грі

В процесі спільної роботи над завданнями проявляються індивідуальні схильності конкретних учнів. Таким чином, відповідно до індивідуальних можливостей учнів, відбувається розподіл ролей Доповідача, Опонента та Рецензента. Важливо, що уся команда в процесі підготовки стає "єдиним механізмом", де кожен учень відчуває іншого, знає його можливості. Турнір – це гра за конкретними правилами, які команда повинна досконало знати і виконувати. До складу команди входять переважно п'ять учнів (за правилами турнірів від 3 до 5). Бажано, щоб, крім 11-класників, у команді були учні 10 чи 9-го класу. Це дає можливість зберегти наступність і набути досвіду для майбутніх турнірів. Під час одного бою розігрується три задачі. Команди по черзі виступають у ролях Доповідача, Опонента, Рецензента. Команда Опонент задає задачу команді Доповідачу, третя команда виступає у ролі Рецензента. Надалі ролі змінюються. Важливо допомогти дітям детально розібратися в особливостях кожної ролі.

Відповідно до правил, Доповідач (один або декілька членів команди) має чітко викласти суть розв’язання задачі й отриманий результат, акцентуючи увагу слухачів на основних математичних ідеях, висновках, узагальненнях, чи визначити окремі суттєві просування в задачах дослідницького характеру. Доповідь має бути чітка, конкретна, лаконічна, представлений розв'язок повинен бути аргументованим При цьому бажано використовувати заздалегідь підготовлені малюнки, плакати, фотографії, відео фрагменти, слайди.

Усвідомити суть ролі Опонента та Рецензента учням значно складніше, ніж роль Доповідача. Опонент (один або декілька членів команди) відмічає позитивні та негативні моменти розв'язку, дає критичні зауваження до доповіді, задає запитання, які характеризують недоліки і помилки у розумінні проблеми і методах її розв'язку. Опонент має чітко визначити всі позитивні, на його думку, моменти виступу Доповідача, найбільш вагомі , з його точки зору, результати, продемонструвати розуміння кожного  з етапів запропонованого розв’язання, зробити висновок щодо їх правильності та повноти, у толерантній формі вказати на всі помилки та недоліки. При цьому Опонент має утримуватися від коментарів, не пов’язаних з доповіддю, не зводити виступ до власного розв’язання задачі.

Рецензент (один член команди) має дати коротку оцінку виступам Доповідача и Опонента, підбити підсумок бою, вказавши, чи розкрита тема (чи правильно розв’язана задача), чи правильними та обґрунтованими були твердження під час доповіді та полеміки. Рецензент має право ставити питання і доповідачу, і опоненту. Хоча і балів за рецензію команда отримує найменше, але роль Рецензента є найважчою, оскільки потрібно відмітити як негативні, так і позитивні сторони представленого розв'язку і опонування, звернувши особливу увагу на те, що не було помічено Опонентом. Необхідно відмітити теоретичні помилки і неточності, якщо такі були допущені в ході доповіді, опонування та полеміки.

Дуже важливо налаштувати учнів на те, що під час бою працює уся команда. Кожен повинен включитися у роботу. Важливо почути і зафіксувати всі зауваження (як позитивні, так і негативні), швидко відшукати аргументи, які будуть використані як при опонуванні та рецензуванні, так і в ході загальної полеміки. Максимально ефективно слід використати ті хвилини, що даються для підготовки опонування та рецензії. Тому відповідно до індивідуальних особливостей в команді повинні бути: лідер, який вміє мобілізувати команду та приймати стратегічні рішення; мозковий центр з глибокою теоретичною базою; психологічний стабілізатор; упорядник ідей; група швидкого реагування, що відшукує теоретичні  та практичні помилки суперника, коректно і швидко формулює запитання.

Отож розпочинається підготовча робота. Вчителі та учні беруть участь в семінарах «Методи розв'язування турнірних задач», які проводять викладачі СНУ. Проводиться ретельний запис усіх запропонованих варіантів чи напрямів розв'язування (працює дивергентне мислення – мислення "вшир"). Результатом є кілька висунутих ідей розв'язання конкретного завдання.

Далі проводиться аналіз кожної ідеї, їх детальне обговорення. Цей етап ми називаємо "критика", оскільки він відбувається у формі жвавої дискусії з аргументацією позитивних і негативних сторін кожної гіпотези. Цей етап є чи не найважливішим – він завершується як формуванням робочої гіпотези для Доповідача, так і аргументацією відхилення інших розв'язків для Опонента і Рецензента. Здавалося б, що задача уже розв'язана. Але розв'язок у такому вигляді не може бути успішно представлений і захищений у турнірному бою. Необхідно провести глибокий аналіз теоретичних кроків, практичних перетворень. На цьому етапі працює конвергентне мислення - мислення "вглиб". Необхідно опрацювати багато інформації, детально розібратися у теоретичних основах даної проблеми. І тут учням особливо необхідна допомога вчителя. Адже часто турнір вимагає глибокого опрацювання тих розділів навчального матеріалу, які за програмою ще не вивчалися. В результаті розробки розв'язання готується чорнова доповідь. На її обговорення запрошуються не тільки члени команди, а й всі зацікавлені вчителі математики та учні. Корисно, щоб на такі обговорення потрапляли люди різного фаху, різного віку з нестандартним мисленням. У кожного з присутніх свій погляд на представлене рішення, що дає змогу поглянути на проблему під різними кутами зору. Проблема атакується з усіх сторін. Така атака дає можливість передбачити питання Опонента, виявляє слабкі або сильні сторони у теоретичних знаннях Доповідача, готує його до справжнього бою. Важливо фіксувати усі конструктивні запитання, зауваження та поради. Це стане в пригоді при опонуванні та рецензуванні даного питання. Іноді доповідь такої атаки не витримує. Тоді необхідно повернутися до іншого розв'язання або знайти доведення необґрунтованих фактів. Якщо ж доповідь і доповідач вистояли, то можна переходити на заключний етап – "шліфування".

Необхідно виготовити наочність – таблиці, схеми, малюнки, підготувати презентації. До цього можна залучати вболівальників. Вони ж запрошуються на рольові ігри, які проводяться для усвідомлення ролі Опонента та Рецензента. Важливо провести роботу над культурою виступу та ведення полеміки. Варто до цього залучити вчителів української мови, випускників, які мають досвід у проведенні турнірів. Задачу вважаємо розв'язаною, якщо готовий до представлення чистовий варіант спільного розв'язку, зібрано нотатки для аргументованого опонування інших розв'язків і команда має необхідну теоретичну базу з даної задачі.

2.2.3. Зразки доповідей міського турніру 2015 року, які підготували учні Луцької гімназії № 4 імені Модеста Левицького

 

Задача 14. «Композиція тригонометричних функцій»

Позначимо через M сукупність функцій y = sinx , y = arcsinx , y = cosx ,

y = arccosx , y = tgx , y = arctgx , y = ctgx , y = arcctgx. Чи iснує таке n ∈ N i такі функції f ₁ ∈ M , f ₂ ∈ M ,..., f _n ∈ M , що f  ₁  (f ₂   (...f _n  (2015)...)) = 1?

Доповідач Лещук Олександр.

Шановні члени журі та учасники турніру!  Пропонуємо вашій увазі розв'язання задачі «Композиція тригонометричних функцій» командою нашої гімназії. Для простішого сприйняття розв'язання задачі нагадаю, що композицією декількох функцій є функція, побудована з двох функцій таким чином, що результат першої функції є аргументом другої.

Композиція функцій f: X → Y та g: Y → Z будується так: аргумент x з X застосовується до першої функції f, а її результат y з Y застосовується як аргумент до другої функції g.

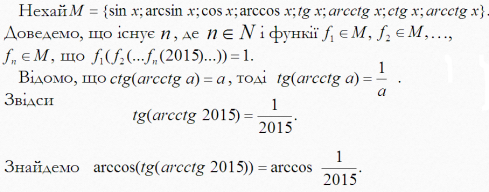
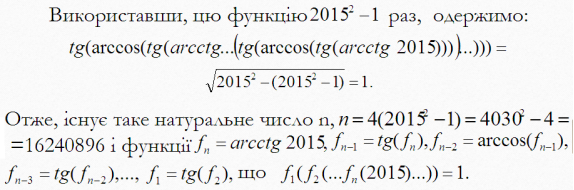
Відповідь: n = 16240896; функції існують.

Доповідь завершено. Дякую за увагу!

Задача 24. «Діаметрально протилежні точки»

Вписане коло ω трикутника ABC дотикається до його сторін BC , CA i AB в точках D , E i F відповідно. Нехай точки X , Y i Z кола ω діаметрально протилежні точкам D, E i F відповідно. Прямі AX, BY i CZ перетинають сторони BC , CA i AB в точках D^’, E^’ i F^’ вiдповiдно. На відрізках AD^’, BE^’  i CF^’ вiдмiтили точки X^’ , Y^’ i Z^’ відповідно так, що D^’ X^’ = AX, E^’ Y^’ = BY, F^’ Z ^’= CZ. Доведіть, що точки X^’ , Y^’ i Z^’  збігаються.

Доповідач Александров Владислав.

Шановні члени журі та учасники турніру! Пропонуємо вашій увазі розв'язання задачі «Діаметрально протилежні точки» командою нашої гімназії.

Геометрична задача  на комбінацію кола, трикутника й діаметрально протилежних точок є досить цікавою та складною.

Нехай на даному малюнку зображено трикутник ABC, який дотикається до його сторін BC , CA i AB в точках D , E i F відповідно. Точки X , Y i Z кола ω діаметрально протилежні точкам D, E i F відповідно. Прямі AX, BY i CZ перетинають сторони BC, CA i AB в точках D^’, E^’ i F^’ відповідно. На відрізках AD^’, BE^’ i CF^’ вiдмiтимо точки X^’, Y^’ i Z^’ відповідно так, що D^’ X^’ = AX, E^’ Y^’= BY, F^’ Z ^’= CZ. Доведемо, що точки X^’, Y^’ i Z^’ збігаються.

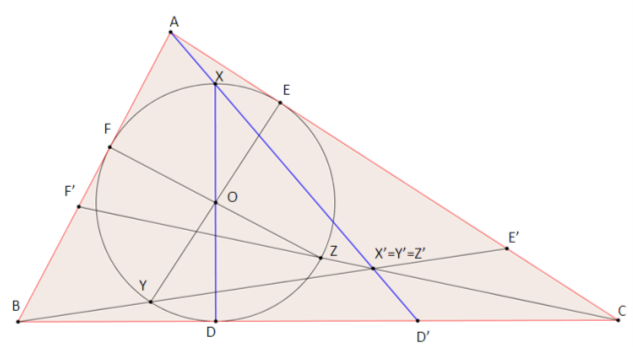
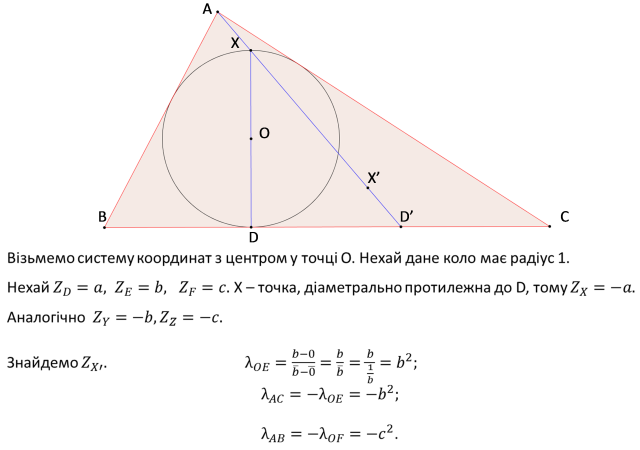
Отже, точки X^’, Y^’ i Z^’ збігаються, що й треба було довести.

Доповідь завершено. Дякую за увагу!

Задача 6. «Країна чотирьох островів»

На островах A , B i C проживає по 2000 чоловік, а на островi D — 2015 чоловiк. Щодня в країнi вiдбувається переселення: з одного з островiв перебираються на кожен з решти островiв по однiй людинi. Чи може через певну кiлькiсть днiв статися так, щоб на островi A опинилося 2015 мешканцiв, а на островах B, C i D — по 2000 мешканцiв?

Доповідач Лещук Олександр.

Шановні члени журі та учасники турніру! Наша команда пропонує один із способів розв’язання  даної задачі.

Доповідь завершено. Дякую за увагу!

Задача 11. «Перестановка чисел»

Нехай b ₁ , b ₂ , ... , b _n — довільна перестановка заданих невід’ємних дійсних чисел a ₁ , a ₂ , ... , a _n . Доведіть, що

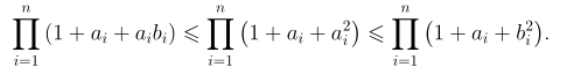
Доповідач Жигалло Микола.

Доброго дня всім учасникам турніру!  Із задоволенням  хочу представити задачу, для розв’язання якої застосовано всім вам відомий метод математичної індукції.

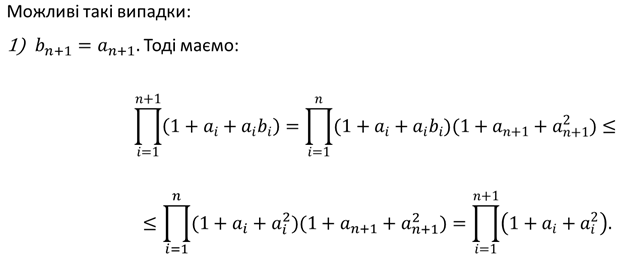
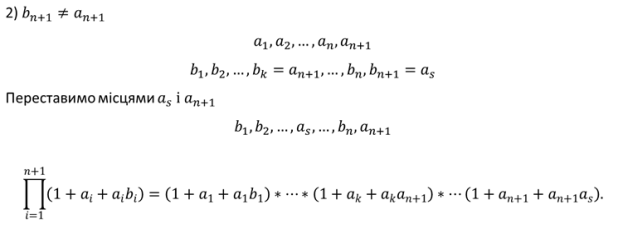
Доповідь завершено. Дякую за увагу!

 

2.2.4. Як опонувати та рецензувати

Як готувати опонування?

На опонування відповідних задач команда налаштовується завчасно – адже вона сама задає задачу Доповідачу. Проте сам процес опонування передбачити неможливо. Які сюрпризи підготував суперник – бездоганну доповідь, у якій, крім позитиву, необхідно знайти недоліки, чи необґрунтоване власне розв'язання задачі? Слабку доповідь опонувати важче, ніж сильну. Проблема в тому, що Опонент не має права нав'язувати своє розв'язання задачі, а повинен аналізувати ту доповідь, яка представлена Доповідачем.

Подаємо один із прикладів опонування. На міському турнірі нашій команді довелося опонувати задачу «Композиція тригонометричних функцій»

Зразок опонування (підготував Лещук Олександр). Дякуємо Доповідачеві за представлений розв'язок задачі. Слід відмітити, що доповідь була чітка, структурована, основні моменти викладені доступно та у логічній послідовності. Як справжній математик, Доповідач запропонував модель розв'язання задачі, від простого до складного. Було достатньо зрозуміло вміле використання властивостей обернених тригонометричних функцій, багаторазове знаходження їх значень.

Але у доповіді не достатньо обґрунтоване саме розв'язання задачі. Окрім цього, у ході доповіді було допущено ряд помилок. Зокрема, Доповідач  неправильно вказав обмеження на функцію y = arcctgx. Доповідач не наголосив на особливостях перетворень композиції тригонометричних функцій. Задача не була узагальнена. В висновку не прозвучало конкретне число n ∈ N, та конкретні  тригонометричні функції f ₁ ∈ M , f ₂ ∈ M ,..., f _n ∈ M , що f  ₁  (f ₂   (...f _n  (2015)...)) = 1. Таким чином, на думку нашої команди, задача розв'язана не повністю, розв'язок не є достатньо аргументованим.

Далі між Доповідачем та Опонентом розпочинається полеміка. Доповідач відповідає на зауваження Опонента, висловлює свої зауваження щодо опонування.

Нарешті в дискусію вступає Рецензент, він задає уточнюючі запитання та має 1–2 хвилини на підготовку рецензії. Навести конкретний приклад рецензування неможливо – адже для цього потрібно знати весь хід турнірного бою. Рецензія починається з подяки Доповідачеві за представлений розв'язок задачі та Опоненту за проведене опонування. Далі подається загальна оцінка доповіді та виступу Опонента. Рецензент повинен вказати на помилки та неточності, зроблені Опонентом, та ті помилки Доповідача, які Опонент не помітив. Проблема у тому, що рецензування не повинно дублювати опонування. Рецензент дає детальну оцінку виступу Доповідача, якщо його думка не збігається з оцінкою Опонента. Слід не забувати, що, окрім аналізу доповіді та опонування, Рецензент повинен проаналізувати ще й полеміку між Доповідачем та Опонентом.

Найчастіше на рецензію відважуються найдосвідченіші члени команди. У цьому випадку найважливіше правильно зіграти роль. Проте, якщо досвідчений учень не володіє необхідними знаннями з даного питання – навіть досвід йому не допоможе. Окрім того, команда не обирає задачу, що випадає на рецензію. І можливий випадок, коли на рецензії розігрується задача того учня, що уже виступив у ролі Доповідача та Опонента. А за правилами турніру не можна виступати за один бій тричі. На рецензію повинен іти інший учасник. Ось чому важливо обговорювати усі турнірні завдання повним складом команд. Після рецензії Доповідач та Опонент відповідають на зауваження Рецензента і відбувається полеміка між ними. Через певний час оголошується загальна полеміка, у якій можуть взяти участь усі члени команд. І саме тут  видно чи є командна гра!

До побачення, “АЛЬФА + ОМЕГА”!

 

2.2.5. Гордість Луцької гімназії № 4 імені Модеста Левицького

2008 р. – ХІ Всеукраїнський турнір юних математиків (м. Луцьк) - (ІІ місце).

2009 р. -  ХІІ Всеукраїнський турнір юних математиків (м. Луганськ) – команда Луцької гімназії № 4 імені Модеста Левицького (ІІ місце).

Богдан Школа та Оксана Сухович – доповідачі ХІ Всеукраїнського турніру юних математиків

Команда переможців ХІІ Всеукраїнського турніру

юних математиків під час гри

Рудь Тетяна – доповідач ХІІІ Всеукраїнського турніру юних математиків

 

2010 р. – ХІІІ Всеукраїнський турнір юних математиків (м. Миколаїв) – команда Луцької гімназії № 4 ім. Модеста Левицького - (учасник).

2011 р. – ХІV Всеукраїнський турнір юних математиків (м. Львів) – команда Луцької гімназії № 4 ім. Модеста Левицького - (учасник).

2014 р. - ХVІІ Всеукраїнський турнір юних математиків (м. Чернівці) – збірна команда «Волинь» - учень Луцької гімназії № 4 імені Модеста Левицького  Александров Олександр - (ІІІ місце).

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 1. Агафонова О. О. Інтерактивні форми і методи роботи на уроках математики                               / О. О. Агафонова // Математика в школах України. – 2005. – № 8 (92). – С. 2– 6.

2. Алгебра і початки аналізу: Підручник для 10–х  класів з поглибленим вивченням математики / А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський, М. С. Якір. – Х. : Гімназія, 2010. – 411 с.

3. Афонькин С. Ю. Все об оригами / С. Ю. Афонькин, Е. Ю. Афонькина. – СПб. : Кристалл, 2005. – 272 с.

4. Афонькин С. Ю. Уроки оригами в школе и дома / С. Ю. Афонькин, Е. Ю. Афонькина. – М. : Аким, 1998. –  300 с.

 5. Афонькин С. Ю. Оригами на праздничном столе / С. Ю. Афонькин, Е. Ю. Афонькина. — М. : Изд-во Аким, 1996. — 30 с.

6. Афонькин С. Ю. Волшебные шары – кусудамы / С. Ю. Афонькин, Е. Ю. Афонькина. —  СПб. : Издательский Дом «Кристалл», 2001. — 160 с.

 7. Балдіна Л. М. Розвиток творчої компетентності учнів на уроках математики   / Л. М. Балдіна // Математика в школах України. – 2006. – № 29 (149). – С.14.                    

8. Белим С. Н. Задачи по геометрии, решаемые методами оригами / С. Н. Белим. — М. : Аким, 1998. — 63 с.

9. Галкин Е. В. Нестандартные задачи по математике. Задачи с целыми числами: Учебное пособие для учащихся 7–11 кл. /  Е. В.  Галкин. – Челябинск: Взгляд, 2005. – 271 с.

10.  Геометрія: Підручник для 8–х класів з поглибленим вивченням математики    / А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський, М. С. Якір. – Х. : Гімназія, 2008. – 239 с.

11. Германович П. Ю. Сборник задач по математике на сообразительность: Пособие для учителей / П. Ю. Германович. – М. : Учпедгиз, 1960. – 224с.

12. Головина Л. И. Индукция в геометрии / Л. И. Головина, И. М. Яглом. – М. : Физматгиз, 1961. – 101 с.

13. Голубев В. И. Решение сложных и нестандартных задач по математике / В. И. Голубев. – М. : ИЛЕКСА, 2007. – 252 с.

14. Гончар В. В. Модульное оригами / В. В. Гончар. – М : Айрис-пресс, 2009. – 112 с.

15. Егоров А. А. Олимпиады «Интеллектуальный марафон». Математика / А. А. Егоров, Ж. М. Раббот. –  М. : Бюро Квантум, 2006. – (Библиотечка «Квант»).

16. Заочные математические олимпиады / Н. Б. Васильев, В. Л. Гуттенмахер,  Ж. М. Раббот, А. Л. Тоом. – 2-е  изд. – М. : Наука, 1987. – 176 с.

17. Клочко І. Я. Нестандартна математика. Тестові завдання. 7 клас: Посібник для підготовки до математичних турнірів та олімпіад / І. Я. Клочко  – Тернопіль: Навчальна книга – Богдан, 2010. – 128 с.

 18. Лось В. М. Математика: навчаємо міркувати. Розв'язування нестандартних задач: Навч. посібник / В. М. Лось, В. П. Тихієнко.  – К. : Кондор, 2005 – 312 с.

19. Мандражи О. Оригаметрія як нова математична теорія / О. Мандражи, М. Федунов // Математика в школах України. – 2008. – № 36 (228). – С.13.

20. Острун Н. Д. Оригами. Мозаики / Н. Д. Острун, А. В. Лев. – М . : Айрис-пресс, 2006. — 144с.

21. Положення про Всеукраїнські учнівські олімпіади, турніри, конкурси з навчальних предметів, конкурси-захисти науково-дослідницьких робіт, олімпіади зі спеціальних дисциплін та конкурси фахової майстерності. Наказ Міністерства освіти і науки, молоді та спорту України № 1099 від 22.09.2011 р. Реєстрація в Міністерстві юстиції України 17 листопада 2011 р. за N 318/20056.

22.  Рабець К. Математичний турнір: змагання, що навчає і виховує: Навчальний посібник / К. Рабець. – К. : Шк. світ, 2009. – 128 с. – (Бібліотека «Шкільного світу»).

23. Рубльов Б. В. Математичні олімпіадні змагання школярів України: 2007 –2008 та 2008 – 2009 р. / Б. В. Рубльов. – Львів: Каменяр, 2010. – 549 с.

24. Розвиток математичних здібностей у школярів. Всеукр. дистанц. наук.-метод. конф. з міжнарод. участю. «ІТМ*плюс – 2011» / В. Г. Бевз. – м. Суми.   С. 16 – 18.

25. Сержантова Т. Б.  365 моделей оригами / Т. Б. Сержантова. — М. : Айрис-пресс, 2010. — 192 с.

26. Тарасюк Т. І. Форми і методи роботи з метою активізації пізнавальної      діяльності учнів / Т. І. Тарасюк // Математика в школах України. – 2006. – № 323 (152). – С. 5 – 10.

27. 35-й Турнир имени М. В. Ломоносова 30 сентября 2012 года. Задания. Решения. Комментарии / Сост. А. К. Кулыгин. – М. : МЦНМО, 2014. – 224 с.

28. Чен Н. В. Надзвичайні вироби своїми руками / Н. В. Чен. – Харків : Книжковий Клуб «Клуб сімейного Дозвілля», 2007. – 240 с.

29. Юртакова А. Е. Об’ємні фігурки  / А. Е. Юртакова, Л. В. Юртакова. – Донецьк: «Видавництво СКІФ», 2007. – 64 с.

30. Ясінський В. А. Геометричні задачі: Готуємося до математичної олімпіади / В. А. Ясінський. – Львів: Каменяр, 2003. – 76 с.

 

Інтернет джерела

1. http://esnuir.eenu.edu.ua/bitstream/123456789/4069/1/Zimych%20A.I.%20Zimyc

h%20T.F..pdf  – Турнірна задача як елемент самостійної дослідницької діяльності учнів.

2. http://kvant.mirror1.mccme.ru/ – Фізико-математичний журнал «Квант» (завдання різних математичних олімпіад ).

3. http://www.origamiart.info/ –  Уроки оригами: от простого к сложному. 

4. http://pedsovet.org/component/option,com_mtree/task,viewlink/link_id,111141/

Itemid,5461250/ – Проект "Оригами – математика!"

5. http://www.ukrreferat.com/index.php?referat=77653 – Оригамі – оригінальний підхід до розв'язування математичних задач.

6. http://ukrtym.blogspot.com/ http://ukrtym.blogspot.com/ – Всеукраїнський турнір юних математиків імені професора М. Й. Ядренка.

7. http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?I21DBN=LINK

&P21DBN=UJRN&Z21ID=&S21REF=10&S21CNR=20&S21STN=1&S21FMT=ASP_meta&C21COM=S&2_S21P03=FILA=&2_S21STR=Npchduped_2012_188_176_14 – Матеріали математичних турнірів як джерело задач дослідницького характеру для роботи в системі МАН.