Завдання для І етапу Всеукраїнської олімпіади з математики (5 -11класи)

Завдання  для І етапу Всеукраїнської олімпіади з математики

5. клас

 

1. (3 бали ) За допомогою дій та чотирьох цифр 5 склади вираз, значення якого дорівнює 12.

2. (5 балів ) Із сірників склали фігуру (див рисунок).  Забери 3 сірники так, щоб залишилось 7 рівних квадратів.

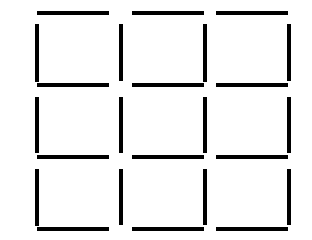
3. (5 балів ) Два землекопи викопають 2 метри канави за 2 години.  Скільки землекопів за 5 год викопають  5м канави.

4. (5 балів ) У трьох класах 119 учнів. У другому класі на 4 учні більше, ніж у першому, а в третьому на три більше, ніж у другому. Скільки учнів у кожному класі.

5. (7 балів ) Якщо до деякого двоцифрового числа приписати справа  нуль, то це число збільшиться на 252. Знайти це число.

 

 

 

 

Завдання  для І етапу Всеукраїнської учнівської олімпіади з математики

6 клас

 

1. (3 бали ) Знайдіть площу городу прямокутної форми, якщо людина обходить його за 5 хв зі швидкістю 20 м/хв. Відомо, що ширина городу 20 м.

 

2. (5 балів) Розв’яжіть ребус:

                                                                                               

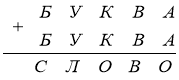
3. (5 балів) Доведіть, що будь-яке число, записане трьома однаковими цифрами, ділиться націло на 37.

 

4. (5 балів) Є аркуш паперу. Його розрізають на 4 частини,  потім деякі частини знову розрізають на 4 частини і т.д. Чи можна при цьому дістати 50 частин аркуша?

 

5. (7 балів) Зараз вік сестри відноситься до віку брата як  4 : 3. Скільки років кожному, якщо 10 років тому сестра була вдвічі старша за брата.

 

 

 

 

 

 

 

 

 

Завдання  для І етапу Всеукраїнської учнівської олімпіади з математики

7 клас

 

1. (3 бали )  Чи існують цілі числа x, y і z, що задовільняють рівняння      28x +30y+ 31z = 365?

 

2. (5 балів ) Вася в Інтернеті знайшов книгу відомого письменника. У книзі було 208 аркушів. Прочитавши книгу, Вася вирішив, що вся потрібна йому інформація знаходиться на декількох, а саме 25 листах, які він і скачав з Інтернету. Вася, як справжній математик, став шукати закономірність в потрібних сторінках книги і склав всі 50 чисел, якими вони нумерувалися. Чи могло у нього вийти 2010?

 

3. (5 балів ) Дано дошку 9 × 9, в кожній клітинці якої стоїть по шашці. За один хід можна зняти будь-яку кількість поспіль шашок в стовпці або в рядку. Програє той, хто не може зробити ходу. Хто виграє при правильній грі і як він повинен грати?

 

 

4. (5 балів ) Множене збільшили на 50%, а множник зменшили на 16%. Як змінився   добуток?

 

5. (7 балів ) Знайдіть площу фігури, зображеної на малюнку, якщо площа однієї клітинки дорівнює 1.

     

 

 

 

 

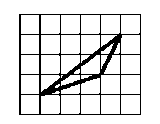
Завдання  для І етапу Всеукраїнської олімпіади з математики

8 клас

1. (3 бали ) Розв’язати рівняння:

2. (5 балів ) Якщо до запису деякого числа дописати справа цифру 9 і до утвореного таким чином числа додати подвоєне початкове число, то одержимо число 633. Знайти дане число.

3. (5 балів ) Побудувати графік функції 

4. (5 балів ) ABCD - квадрат, AD = ВЕ = СЕ. Знайдіть кут AED, якщо Е- довільна точка.

 

5. (7 балів ) Довести, що з будь-яких дев’яти натуральних чисел можна вибрати два, різниця яких ділиться на 8 .

 

 

 

 

 

 

 

 

 

 

 

 

Завдання  для І етапу Всеукраїнської олімпіади з математики

9 клас

1. (3 бали ) Розрізати трикутник на дві частини так, щоб з них можна було скласти паралелограм.

2. (5 балів ) Побудувати графік функції .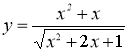

3. (5 балів ) Довести, що , якщо , .

 

4. (5 балів ) Дано рівняння .

При якому значенні а  , де і - корені даного рівняння.

 

5. (7 балів ) Один з кутів рівнобедреного трикутника дорівнює 120º. З середини

основи опущено перпендикуляр на бічну сторону. В якому відношенні

основа перпендикуляра ділить бічну сторону?

 

 

 

 

 

Завдання для I етапу Всеукраїнської учнівської олімпіади з математики

10 клас

 

1. (3 бали) Розв’яжіть нерівність: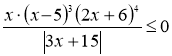

 

2. (5 балів) При яких значеннях параметра корені рівняння є додатними  числами?

 

 

3. (5 балів) Для додатних чисел  х,  у  і  z доведіть нерівність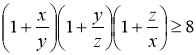

 

4. (5 балів) На бічних сторонах АВ і ВС рівнобедреного трикутника АВС взятоточки Е та F відповідно. Відрізки ЕС та FА перетинаються в точці О. Доведіть, що якщо площа чотирикутника ВЕОF дорівнює площі трикутника АСО, то АЕ = ВF

 

5. (7 балів)  На дошці записано числа від 3 до 22. За один крок дозволяється пару чисел х, у замінити на число х+у+5ху. Чи можна наприкінці дістати число 20112014?

 

 

 

 

 

 

 

        

 

 

 

 

Завдання для І етапу Всеукраїнської учнівської олімпіади з математики

 

11 клас

 

1. (3 бали ) Обчислити  .

 

2. (5балів) Розв’язати систему рівнянь:

 

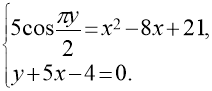
3. (5 балів) В трапецію вписано коло радіуса r. Знайдіть площу трапеції, якщо

кути при більшій основі рівні α та β.

 

4. (5 балів) Знайти значення параметра а,  при якому система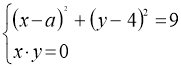

має єдиний розв’язок.

 

5. (7балів) Додатнi числа x,y,z задовольняють умову  xyz = 1. Доведiть нерiвнiсть

x + y + z ≤ х²+ y²+ z².