І. І. ТЕЛИЧКО

Методика використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії в загальноосвітніх навчальних закладах різних типів та у вищих навчальних закладах І-ІІ рівнів акредитації

Навчальний посібник

 

 

 

 

 

 

 

 

 

 

Кам’янець-Подільський

                                                                                                  2011                                                 

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

КАМ’ЯНЕЦЬ-ПОДІЛЬСЬКА ШКОЛА І-ІІІ СТУПЕНІВ №1 З ПОГЛИБЛЕНИМ

ВИВЧЕННЯМ НІМЕЦЬКОЇ МОВИ 

І. І. ТЕЛИЧКО

Методика використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії в загальноосвітніх навчальних закладах різних типів та у вищих навчальних закладах І-ІІ рівнів акредитації

Навчальний посібник

 

 

 

 

 

 

 

 

Кам’янець-Подільський

                                                                                                  2011                                       

Автор:       І.І. Теличко, вчитель математики Рецензент:  М.Л. Павлуцький, вчитель математики.

Теличко І. І.

Методика використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії в загальноосвітніх навчальних закладах різних типів та у вищих навчальних закладах І-ІІ рівнів акредитації: навчальний посібник / І. І. Теличко. – Кам’янець-Подільський: Кам’янець-Подільська школа І-ІІІ ступенів №1 з поглибленим вивченням німецької мови, 2011. – 45 с.

У посібнику розкрито роль і значення наочності при вивченні шкільного курсу математики, розглянуто види наочних посібників, комп’ютер як наочний посібник на уроках геометрії, викладено методику використання наочних посібників на уроках геометрії в середніх загальноосвітніх навчальних закладах різних типів та у вищих навчальних закладах І-ІІ рівнів акредитації.

Для вчителів математики середніх загальноосвітніх навчальних закладів, студентів педагогічних вищих навчальних закладів.

 

 

 

 

© І. І. Теличко, 2011

          

ЗМІСТ

Вступ…………..…….………………………..…………………………………..3

І. Наочність в навчальному процесі як принцип дидактики

§ 1. Роль і значення наочності в навчально-виховному процесі …..........7

§ 2. Типи наочних посібників з математики, їх характеристика ……....17

§ 3. Аналіз психологічної, дидактичної і методичної літератури по темі дослідження ……………………………………….….............................33

ІІ. Методика використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії в загальноосвітніх навчальних закладах різних типів та у ВНЗ І-ІІ рівнів акредитації

§ 1. Методика використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії в загальноосвітніх навчальних закладах …………..………………………………………..46

§ 2. Методика використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії в загальноосвітніх навчальних закладах з поглибленим вивченням математики...………69

§ 3. Методика використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії у вищих навчальних

закладах І-ІІ рівнів акредитації ………………………………………126

Висновки і рекомендації...…………………………..…..…...……...................162

Список використаної літератури…...…………..………...…………….….......166 Вступ

Актуальність теми дослідження. В умовах реформування системи освіти, відтворення і зміцнення інтелектуального потенціалу нації, виходу вітчизняної науки і техніки, економіки і виробництва на світовий рівень, інтеграції в світову систему освіти, переходу до ринкових відносин і конкуренції будь-якої продукції, в тому числі й інтелектуальної, особливо актуальним стає забезпечення належного рівня математичної підготовки підростаючого покоління.

Математика має широкі можливості для інтелектуального розвитку особистості, в першу чергу, розвитку логічного мислення, просторових уявлень і уяви, алгоритмічної культури, формування вміння встановлювати причинно-наслідкові зв’язки, обґрунтовувати твердження, моделювати ситуації та ін.

Визначаючи завдання навчання математики на етапі загальної середньої освіти, необхідно враховувати потреби учнів у математичній підготовці відповідно до того, яке місце вона займе в майбутній трудовій діяльності.

За останні роки у соціальному житті суспільства відбулись значні зміни, що вимагають перегляду системи освіти. Її переорієнтовують у бік демократизації та гуманізації освіти, яка спрямована на виховання, пер за все, особистості, функціонально грамотної і методологічно компетентної, яка володіє інформаційними технологіями, здатна адаптуватися до навколишнього середовища, до аналізу і самоаналізу, до свідомого вибору і відповідальності за нього.

Аналіз сучасного стану системи освіти в Україні говорить про актуальність та необхідність створення єдиного освітнього простору для інформаційно-педагогічного забезпечення освітян всім необхідним для проведення занять з використанням ілюстративного і наочно-навчального матеріалу [41, с.40].

На сьогодні є досить актуальною проблема використання наочності на уроках математики. Необхідно відзначити, що проблеми використання наочності у навчальному процесі висвітлювали відомі дидакти та методисти: Дубравська Д.М. [31], Коменський Я.А. [60], Малафіїк І.В. [72], Іванюта О.В.

[45], Леонтьєв А.Н. [69] та ін.

Незважаючи на наявність досить значної кількості публікацій, методичних рекомендацій, в яких висвітлюється проблема використання наочності під час вивчення тієї чи іншої теми, необхідно зазначити, що, поперше, на сьогоднішній день не існує досконалого всеохоплюючого посібника, який розкривав би повністю методику використання різних видів наочності на уроках геометрії старшої школи, а по-друге, відсутній навчальний комплект наочностей, який би забезпечував ефективне засвоєння учнями програмного матеріалу з теми «Взаємне розміщення прямих і площин в просторі».

Спостерігається тенденція до зменшення кількості тижневих годин, які відводяться на вивчення математики в загальноосвітній школі, особливо там, де математика не є профілюючою дисципліною. Зміст програми та вимоги до знань, умінь та навичок учнів з математики залишаються майже незмінними.

Тому постає проблема щодо ефективного використання часу протягом уроку. Одним із способів такої економії є доцільне використання засобів наочності.

В нині діючих підручниках з геометрії [10, 86] не використовують

методики, яка б забезпечила проведення занять з використанням ілюстративного й наочно-навчального матеріалу.

Все це зумовило вибір теми нашого дослідження «Методика використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії в загальноосвітніх навчальних закладах різних типів і у ВНЗ I-II рівнів акредитації».

Об’єктом          дослідження       є        процес        навчання    математики в загальноосвітніх навчальних закладах і у ВНЗ І-ІІ рівнів акредитації.

Предметом дослідження є методика використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії в загальноосвітніх навчальних закладах різних типів і у ВНЗ І-ІІ рівнів акредитації.

Мета дослідження полягає в тому, щоб розробити методику використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії в загальноосвітніх навчальних закладах різних типів і у ВНЗ І-ІІ рівнів акредитації, а також у зв’язку з впровадженням в навчально-виховний процес нових інформаційних технологій, які забезпечують подальше вдосконалення навчання, доступність та ефективність освіти, розробити навчальні презентації із застосуванням мультимедійного комплекту, оскільки комп’ютерна підтримка вивчення математики дає наочні уявлення про поняття, що вивчаються.

У процесі дослідження була висунута гіпотеза: розробка та впровадження такої методичної системи, яка б відповідала основним принципам навчання, зокрема, принципу наочності, та забезпечуватиме ефективне засвоєння учнями навчального матеріалу, сприятиме різнобічному розвитку особистості учня та розвиватиме стійкий інтерес до вивчення математики.

Для досягнення мети планується розв’язати наступні завдання:

•      проаналізувати методичну, дидактичну і психологічну літературу по темі дослідження;

•      ознайомитись        з        сучасними інноваційними     та      інформаційними технологіями навчання та спробувати втілити їх у навчальний процес;

•      розробити методику використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії у загальноосвітніх навчальних закладах різних типів та у ВНЗ І-ІІ рівнів акредитації;

•      перевірити експериментально розроблену методику.

Практичне значення дослідження полягає в тому, що розроблена методика допоможе вчителям ефективно використовувати різні види наочності протягом уроку та створити необхідний комплект засобів наочності для впровадження їх у навчально-виховний процес.

Такі дії вчителя дадуть змогу раціонально організовувати навчальну діяльність учнів, робити її цілеспрямованою та продуктивною, а також забезпечити подальше вдосконалення навчально-виховного процесу.

В процесі дослідження використовувались такі методи:

1)                вивчення і використання історії математики і математичної освіти;

2)                вивчення і використання досвіду сучасного навчання математики;

3)                дидактична обробка ідей, методів і мови математики;

4)                експеримент.

          

І. Наочність в навчальному процесі як принцип дидактики

§1. Роль та значення наочності в навчально-виховному процесі

Ефективність реалізації закономірності виховного і розвиваючого характеру навчання зростає за умови, що вчитель знає і враховує під час уроку переконання учнів, їхнє ставлення до знань, глибину усвідомленості, світоглядні ідеї та риси характеру, які формуються в результаті навчання. Першочергове завдання педагога – навчити учнів мислити, виховувати в них прагнення до пізнання нового, до самостійного опанування знаннями. Така здатність формується і розвивається, коли вони мають змогу виявляти власну самостійність і активність.

Процес навчання залежить від вікових та реальних можливостей учнів. Його зміст і методи визначаються передусім з огляду на вікові особливості дітей. Реальні навчальні можливості учнів зумовлені рівнем розвитку інтелектуальної, емоційної та вольової сфер, знань, вмінь, навичок до навчання,ставленням до нього, фізичним станом і працездатністю.

Свідчення цього – у школі різні діти вчаться по-різному [72].

Ефективність процесу навчання залежить від рівня активності учня. Суть цієї закономірності полягає в тому, що результати навчання учня залежать від характеру навчально-пізнавальної діяльності й рівня розвитку його мотиваційної сфери.

Навчання передбачає цілеспрямовану взаємодію вчителя, учня і виучуваного об’єкта. Навіть якщо учень опановує предмет  самостійно за підручником чи додатковою літературою, то вчитель спрямовує його пізнавальну діяльність і контролює її.

Навчальний процес ефективний лише за умови активності учнів. Чим більша різноманітність діяльності учнів на уроці, чим більша інтенсивність їхньої праці, що організована педагогом, тим результативніший процес навчання.

Принципи навчання (дидактичні принципи) – основні положення, що визначають зміст, організаційні форми та методи навчальної роботи школи.

Принцип навчання, відображаючи якийсь один істотний аспект процесу навчання, стає підґрунтям для формулювання правил навчання.

Правила навчання залежать від принципу навчання, конкретизують його, підпорядковуються йому і сприяють його реалізації. Вони мають чітко окреслений характер практичних вказівок, якими користуються в конкретній навчальній ситуації [72].

Одним з головних принципів навчання є принцип наочності, в навчанні він обґрунтований у XVII ст. Я.-А. Коменським у праці «Велика дидактика». Вчений сформулював «золоте правило» дидактики: «…все, що тільки можна, подавати для сприймання відчуттями, а саме: видиме – для сприймання зором, чутне – слухом, запахи – нюхом, смакове – смаком, доступне дотику – через дотик. Якщо якісь предмети одразу можна сприймати кількома відчуттями, нехай вони одразу охоплюються кількома відчуттями…» [60, с. 104].

Залежно від характеру відображення дійсності наочність поділяють на такі види:

                а)                  натуральна – рослини, тварини, знаряддя і продукти праці,

мінерали, хімічні речовини та ін.;

                б)                  зображувальна – навчальні картини, репродукції художніх

полотен, макети, муляжі та ін.;

                в)              схематична – карти, схеми, діаграми, графіки, малюнки тощо

[64]. 

Використання наочності залежить від творчого потенціалу вчителя. Відомий донецький учитель математики В. Шаталов активно використовує малюнки – так звані опорні сигнали, в яких в образно-символічній формі відображено головну суть факту чи явища. Вони настільки прості, що учень може їх запам’ятати і відтворити, зберігаючи в пам’яті за їх допомогою основний зміст нового матеріалу. Головна їхня цінність – сконцентрованість інформаційного змісту, виклад його в такому вигляді, який легко сприймається [30].

Використання наочності у процесі навчання сприяє розумовому розвиткові учнів, допомагає виявити зв'язок між науковими знаннями і життєвою практикою, між теорією і практикою, полегшує процес засвоєння і сприяє розвитку інтересу до знань, допомагає сприймати об’єкт у розмаїтті його сторін і зв’язків, стимулює розвиток мотиваційної сфери учнів. При цьому важливо дотримуватись наступних дидактичних вимог:

§   не перевантажувати процес навчання наочністю – це знижує самостійність і активність учнів в осмисленні навчального матеріалу;

§   потрібна чітка мета використання наочних засобів у структурі уроку (коли ввести, з якою метою, який висновок буде зроблено);

§   вивішування заздалегідь усіх наочних засобів дезорганізовує сприймання учнів, розсіює їхню увагу – учні повинні у потрібний момент зосередитись лише на необхідному об’єкті, решта мають бути закриті;

§   наочний об’єкт не повинен містити нічого зайвого, щоб не викликати в учнів побічних асоціацій;

§   використовуючи наочність, необхідно зважати на вік школярів [64].

Як відомо, вихідним моментом у пізнанні оточуючого світу є споглядання. «Від живого споглядання до абстрактного мислення, а від нього до практики – такий діалектичний шлях пізнання істини, пізнання об’єктивної реальності» [66, с.142].

Проте стосовно математики цей закон можна сформулювати так:

математизація емпіричного матеріалу → логічна організація математичного матеріалу → застосування математичної теорії.

Процес навчання математики складає діалектичний процес взаємозв’язку діяльності вчителя і учня через навчальний предмет. Зміст та методи навчання тісно пов’язані між собою. Новий зміст потребує розробки нових методів, які в свою чергу дозволяють змінювати зміст навчання [58].

Принцип наочності випливає із суті процесу сприйняття, осмислення і узагальнення учнями матеріалу, що вивчається. Він означає, що в навчанні необхідно, приймаючи до уваги логіку процесу засвоєння знань, на кожному етапі навчання знайти його вихідний початок у фактах і спостереженнях одиничного або в аксіомах, наукових поняттях і теоріях, після чого визначити закономірний підхід від сприйняття одиничного, конкретного предмета до загального, абстрактного або навпаки – від загального, абстрактного до одиничного, конкретного [35, с.22].

Наочність збагачує     коло уявлень       дитини,       робить        навчання доступнішим, конкретним і цікавим, розвиває спостережливість і мислення.

Методично правильно побудоване навчання математики повинно починатися з конкретного і поступово переходити до абстрактних висновків. Переходу від сприймання конкретного до абстрактного і від абстрактного до конкретного сприяють засоби навчання.

Під засобами навчання математики розуміють сукупність об’єктів будь-якої природи, кожний з яких повністю або частково замінює поняття, яке вивчається, дає нову інформацію про нього.

У навчанні використовуються різні засоби: підручники, навчальні посібники для учнів (картки з математичними завданнями, зошити з друкованою основою, довідники тощо), спеціальні наочні посібники (предмети або їх зображення, розрізні цифри, знаки дій і порівняння, моделі геометричних фігур), інструменти й прилади (лінійка, циркуль, кутник, палетка), технічні засоби навчання [35].

Розглянемо основні напрями застосування наочних посібників при вивченні даної теми.

Насамперед підкреслимо ту важливу роль, яку відіграє унаочнення в процесі формування в учнів певних математичних понять. Сюди належить, наприклад, демонстрування різних графіків, а також їх складових елементів. Внаслідок такого демонстрування в учнів створюються певні образи, які потім за допомогою аналізу і синтезу можуть перерости у відповідні поняття і стати надалі об’єктом розумової діяльності учня, спрямованої на розкриття тих або інших закономірностей реальної дійсності.

Не менше значення має унаочнення при підведенні учнів до «перевідкриття» того або іншого математичного твердження, яке має бути доведено. Думку учня спрямовують так, що в нього виникає певна догадка відносно закономірності, яка має бути встановлена; так виникає своєрідна гіпотеза, яка потім за допомогою міркувань або буде остаточно встановлена і перетворена в реальний факт, або ж буде спростована, коли вона не відповідає реальній дійсності. Внаслідок такого підходу значно підвищується активність учнів і їх інтерес до навчання; разом з тим і набуті знання стають більш свідомими, міцними, глибокими.

Щодо використання, то наочні посібники поділяють на загальнокласні та індивідуальні. Загальнокласними користується відразу весь клас. Їх називають ще, іноді, демонстраційними. Індивідуальними користується кожен учень окремо. Часто загальнокласні та індивідуальні посібники бувають однаковими за змістом і відрізняються лише розмірами: моделі геометричних фігур і креслярські інструменти. Важливо правильно розміщувати як загальнокласні, так і індивідуальні посібники, щоб ними зручно було користуватись на уроках.

Залежно від виготовлення розрізняють наочні посібники, виготовлені друкарським способом або на фабриці і саморобні, виготовлені вчителем або школярами.

Саморобні посібники доповнюють готові наочні посібники. Це різні малюнки і креслення для складання задач, збірні геометричні фігури, таблиці, в яких можна замінювати цифри і окремі слова, електрифіковані таблиці множення і додавання. До виготовлення наочних посібників корисно залучати дітей. Це має велике освітнє і виховне значення, сприяє свідомому і міцному опануванню знань і вмінь, допомагає виробити певні трудові навички. Працюючи з посібниками, виготовленими своїми руками, дитина навчається з повагою ставитись до праці. Саморобні посібники мають бути нескладними щодо виготовлення, відповідати нормам шкільної гігієни.

Важливим засобом наочності в процесі вивчення математики є таблиці. За метою застосування вони різноманітні:

-              таблиці для формування математичних понять і закономірностей

(навчальні таблиці);

-              таблиці-інструкції (здебільшого алгоритми виконання арифметичних дій, пам’ятки розв’язування текстових задач);

-              таблиці, що служать засобом відшукання способу розв’язування задачі;

-              таблиці для усних обчислень; - таблиці-довідники.

До дійових засобів наочного навчання в початкових класах відносяться записи і малюнки, виконані вчителем на дошці.

Форма подання структурних схем обчислювальних прийомів може бути різна – залежно від етапу роботи над цим прийомом, мети тощо. Наочна інтерпретація має велике значення для розв’язування задач. Вона може мати вигляд короткого запису, таблиці, схеми, малюнки. При цьому кожний вид наочності може мати різні варіанти. Вибір того чи іншого виду наочності зумовлений передусім дидактичною метою роботи над задачами, розв’язати задачу окремими діями з письмовим поясненням чи без нього, складання виразу з письмовим поясненням чи записати (назвати) відразу вираз; розв’язати задачу різними способами і встановити, який з них раціональний; розглянути тільки залежність між величинами задачі тощо.

Велике значення відіграють також інструменти, прилади і моделі, технічні засоби навчання та засоби зворотного зв’язку.

Знання видів наочних посібників дає змогу учителеві правильно їх добирати і ефективно використовувати під час навчання, а також виготовляти самостійно або разом з дітьми потрібні наочні посібники. Проте потрібно пам’ятати, що наочність не самоціль, а допоміжний засіб навчання. Тому не слід зловживати застосуванням наочності, бо це гальмує активність учнів і затримує розвиток їх логічного мислення. Отже, треба уникати двох крайностей: ігнорування наочності і надмірного її застосування.

При використанні наочних посібників ефективність буде тим вищою, чим більше число органів чуття буде залучено до їх «споглядання». Учень повинен не лише споглядати в справжньому розумінні цього слова, а й безпосередньо діяти: міряти, клеїти тощо. Лише тоді він матиме можливість розкрити всі сторони і залежності спостережуваного об’єкта [5, с.6].

Починаючи вивчати те або інше питання курсу математики, вчитель насамперед повинен з’ясувати, чи є в уяві учнів потрібні чіткі та яскраві наочні образи. Якщо таких немає, то їх спочатку треба створити, бо інакше знання, набуті учнями будуть формальними [5].

Трудність сприймання просторових геометричних і абстрактних математичних співвідношень змушує унаочнювати їх. Дидактика математики вказує математичні моделі як один з найкращих засобів унаочнення. Ці моделі встановлюють взаємозв’язки між абстрактними математичними поняттями і конкретними дійовими образами. Встановлення таких взаємозв’язків потрібне не лише для кращого усвідомлення абстракцій математики, а й для ефективного застосування математичних знань на практиці, в житті [116].

Таким чином, використання та виготовлення наочності в школі, якщо воно правильно організоване, має важливе значення у формуванні позитивних властивостей особистості і рис характеру, забезпечує естетичне, економічне і трудове виховання.

Наочність є обов’язковою якістю будь-якого навчання. Шляхом цілеспрямованих дій ми формуємо в свідомості учня, якого навчаємо, деяку систему понять, відносин між ними. Для того, щоб навчання було успішним, необхідно, щоб учень міг сприймати цю систему і працювати з нею. Але для цього, в свою чергу, необхідно пред’явити учневі деяку її матеріальну модель. Для цього застосовують наочні засоби навчання.

Але зауважимо, що не слід зловживати використанням наочних посібників, не слід забувати, що одним із завдань навчання учнів математики є оволодіння ними навичками абстрактного мислення, а унаочнення має лише допомагати їм у цьому. І якщо учень може при деякому напруженні думки розібратися в тому чи іншому питанні без наочних посібників, то не варто поспішати йому нав’язувати їх, бо це може лише нашкодити справі [5, с.7].

Очевидно, що значення і особливості використання наочних посібників на різних ступенях навчання математики не можуть залишитися незмінними. З підвищенням рівня загального розумового розвитку учнів легше і швидше відбувається перехід від живого споглядання до абстрактного мислення.

Чим молодший вік дитини, тим конкретніше її мислення, тим більше воно потребує опори в конкретних наочних образах. Так, наприклад, дитина дошкільного і молодшого шкільного віку легко уявляє собі три яблука, три кубики чи грибки, але уявити число три без речей, яких воно стосується, для неї дуже важко [5, с.7-8].

Також при вивченні взаємного розміщення прямих і площин в просторі можна використовувати різні робочі і довідкові таблиці. Робочі таблиці – це такі таблиці, за матеріалом яких можна організувати активну розумову діяльність учнів як по засвоєнню нового теоретичного матеріалу, так і по його закріпленню. За допомогою робочих таблиць можливо здійснити виконання великої кількості вправ, які сприяють виробленню і закріпленню певних навичок в учнів. Можна проводити їх опитування або створити проблемну ситуацію перед всім класом. 

На відмінну від робочих таблиць довідкові таблиці, тобто таблиці для запам’ятовування, призначені для тривалої дії на зоровий апарат учнів. Такі таблиці можуть бути вивішені в кабінеті математики на тривалий час.

Таким чином, основною властивістю довідкових таблиць є (крім наочності, яка у ряді випадків відіграє важливу роль) їх дидактична спрямованість. Ці таблиці призначені для примусової дії на пам'ять, що вчиться з метою запам’ятовування основних фактів, формул, графіків тощо. 

Також не можна забувати і про такі засоби навчання як діапозитиви, кодопозитиви, комп’ютерні засоби, які можуть бути ефективно застосовані при вивченні взаємного розміщення прямих і площин в просторі і не тільки цієї теми [12].

Тому, готуючись до конкретного уроку, вчитель вибирає ті засоби, з якими легше організувати необхідну роботу учнів, тобто які найбільш прості для їх сприйняття в даний момент.

Так, щоб деяка матеріальна модель дозволяла організувати засвоєння того чи іншого поняття, вона повинна не тільки правильно його відображати, але й бути простою для сприйняття учнів [64].

Наочні посібники, які застосовуються на уроках, приносять більше користі тоді, коли вони є не тільки простою ілюстрацією до змісту, але й джерелом інформації, чому служать широко практиковані сьогодні у школах навчальні картки [12].

Діяльність учнів із реальними предметами, макетами і конструкціями може здійснюватись як у безпосередньому контакті з ними, так і без нього.

У першому випадку мова йде про власноручне маніпулювання предметами, до якого залучається кожен учень. Такий спосіб використання предметів, макетів і конструкцій є найдоцільнішим. За таких умов в учнів активізується не тільки зоровий канал проходження інформації, а й кін естетичний. Учні через дотик і механічні дії отримують додаткову й досить важливу інформацію про об’єкти споглядання або дослідження. Зрозуміло, що пояснення вчителя при цьому не втрачає своєї вагомості [12].

У другому випадку, який доцільно назвати демонстрацією, учні разом із поясненнями вчителя отримують інформацію, але лише зорову. Хоча вона є важливою, проте не завжди достатньою для учнів. Оскільки діє формула «Краще один раз побачити, ніж сто разів почути», то це означає, що відмовлятись від демонстрацій зовсім не треба.

Організація демонстрацій потребує спеціальної уваги вчителя. Треба, щоб предмети були достатніх розмірів, щоб їх зовнішні дані не суперечили тій внутрішній суті, яку розкриватиме вчитель, щоб кількість фонових елементів була якомога меншою.

Учитель повинен прагнути до комплексного використання засобів наочності, здатних мобілізувати всю сферу сприймань людини.

Використання на уроках математики наочних посібників вимагає від учителя великої педагогічної та методичної майстерності. Готуючись до уроку, вчитель повинен чітко визначити:

-         мету використання наочних посібників;

-         в який момент уроку їх застосовувати;

-         чи слід пропонувати учням самостійно виготовити наочність з даної теми і який саме тощо [12].

Для ефективного використання наочності важливо ретельно підбирати її, враховуючи, який вид наочності найбільш оптимальний, яку функцію він повинен виконувати.

Принципи навчання тісно взаємопов’язані, зумовлюють один одного, жоден з них не може бути використаний без урахування інших. Зокрема, правильно поєднати теорію з практикою можна лише за умови, що навчання є водночас доступне, наукове і систематичне, що вчитель спонукає учнів до творчої діяльності та ін. 

Отже, у процесі навчання вчитель повинен керуватись всіма принципами. Тому, використовуючи наочність на уроках, підвищується ефективність уроків математики.

§2. Типи наочних посібників з математики та їх характеристика

Велике значення в наш час має математика. З абстрактності понять, якими оперує математика, випливає і своєрідна особливість її методу, в основі якого лежить виведення з певних вихідних положень певних висновків за допомогою самих лише міркувань. Як стверджується в [66], вихідним моментом у пізнанні є живе споглядання. Тому, щоб в процесі навчання здійснювати це живе споглядання, треба застосовувати наочні посібники.

Наочними посібниками називають усі предмети (речі, моделі, рисунки, схеми, таблиці), які показують учням у процесі навчання для того, щоб ті, в свою чергу, краще засвоїли програмний матеріал. У математиці наочні посібники використовують для:

ü вироблення в учнів нових понять;

ü пов’язування навчання з життям;

ü полегшення доведення теорем і розв’язування задач [9, с.73-74].

У навчанні математики специфіка змісту та предметної діяльності накладає певний відбиток на особливості невербальних знаково-символічних засобів та характер їх використання у навчальному процесі. Однією з функцій таких засобів є унаочнення змісту в його традиційному розумінні

[9].

Як наочні посібники в процесі навчання математики найчастіше використовують: 1) реальні предмети, що зустрічаються в природі, побуті, техніці тощо; 2) спеціальні моделі, картини; 3) схематичні малюнки, графіки, діаграми та ін. [5].

Здебільшого найкращим наочним посібником є справжня річ. Наприклад, учням набагато краще показати справжній циркуль, ніж його зображення. Але в деяких випадках моделі і схеми для унаочнення кращі, ніж реальні предмети. Наприклад, проілюструвати правила додавання раціональних чисел зручно за допомогою моделі термометра з рухомою стрічкою, на ній можна швидко «змінювати температуру». Справжній термометр для цього не придатний [7, с.74].

У шкільній практиці використовуються два види навчальних карток.

1.     Картки-завдання – це картки, в яких містяться завдання для конкретного уроку.

2.     Картки контролю – це картки, які використовуються для перевірки знань, вмінь і навичок учнів [12].

Є моделі та наочні посібники, які придатні для ілюстрування тільки одного-двох фактів, правил, властивостей, а є й універсальні, які можна використовувати в багатьох випадках. Наприклад, скляна модель трикутної піраміди придатна в основному тільки для того, щоб показати піраміду і її елементи, а спеціальні стереометричні конструктори, які дають можливість конструювати дуже багато різних моделей [103, с.73].

Наочними посібниками бувають також різні інструменти і прилади. Наочні посібники бувають фабричні і саморобні. Акуратнішими і міцнішими є фабричні посібники. Проте, обмежуватись тільки ними не можна, поперше, тому що їх мало випускають, по-друге, виготовлення наочних посібників корисне: виготовляючи той чи інший посібник, учень глибше засвоює поняття, властивість, закономірність, яку цей посібник ілюструє, він привчається виконувати попередні розрахунки і пов’язує виучуваний теоретичний матеріал з виробництвом тощо [12, с.21].

З усіх наочних посібників у математиці найбільш поширеними є малюнки. Особливо часто доводиться користуватися малюнками в геометрії. При доведенні теорем виникає потреба розглядати послідовність зображень фігур чи їх елементів, яка властива даній конкретній теоремі. Така сукупність малюнків визначається сукупністю ланцюгом висновків, які необхідно зробити для доведення певного твердження. Відповідно можна використати інскриптивний метод, за якого вчитель не записує довгих доведень теорем чи розв’язання задач, а робить це усно, користуючись тільки малюнками, схемами [103, с.75].

Вибір наочного матеріалу в учбових цілях повинен здійснюватись з урахуванням психологічної природи образа, що виникає на його основі.

Різні види наочності виконують різні функції. Одні сприяють пожвавленню уявлень, інші становлять опору для абстрактного мислення.

За ступенем абстракції наочні посібники поділяють на образні і необразні [14].

Образні посібники є:

§  натуральні або природні – представляють собою реальні предмети або процеси (об’єкти, явища, роздатковий матеріал та ін.);

§  моделі та макети (модель куба чи призми);

§  образотворчі (фотокартки, малюнки, художні і навчальні картини тощо) використовуються, коли показ натурального предмету неможливий або майже неможливий, а споглядання конкретного образу необхідне;

§  графічні (креслення, ескізи, плани); § умовні (графіки, діаграми).

До необразних посібників відносять:

•      таблиці (наприклад, таблиця «Многокутники та многогранники»);

•      схеми (наприклад, схема виведення формули для обчислення об’єму піраміди).

Залежно    від     призначення        наочні         посібники   поділяють   на демонстраційні та індивідуальні (класні та учнівські) [7].

Залежно від форми – на плоскі та об’ємні. Для плоских посібників характерно те, що зображення в них міститься на площині, при цьому залишаються незмінними ракурс, форма, взаємне розміщення окремих частин.

Одним із видів плоских посібників є таблиці, які поділяють на довідкові, ілюстративні, робочі (таблиці-завдання).

Існують також комбіновані таблиці, в яких поєднується ілюстративна частина із завданнями.

Довідкові таблиці       розраховані          на      довгочасне користування. Застосовування таких таблиць протягом уроку забезпечує економію часу під час розв’язання різних задач та вправ.

Ілюстративні таблиці використовуються під час пояснення нового навчального матеріалу, а на наступних уроках їх можна застосовувати для фронтальної перевірки знань та проведенні самостійних робіт. Крім того, при організації фронтальної і самостійної робіт велика роль відводиться таблицям-завданням. Робота з ними може будуватись у формі усних вправ, диктантів, письмових самостійних робіт, опитувань біля дошки.

На сучасному етапі розвитку психолого-педагогічної науки розрізняють поняття «наочність», «засоби наочності», «прийоми наочності». При такому підході під наочністю розуміють представлення істотного в плані сприйняття; під засобами наочності – конкретні предмети і знаковосимвольні засоби, що використовуються для виділення істотного в плані сприйняття; прийоми наочності – це способи виділення істотного в представленому матеріалі [51].

Технічні засоби навчання – це система засобів, що складається з двох взаємопов’язаних частин: специфічні, наочні навчальні посібники та апаратура, за допомогою якої надається інформація з певного навчального посібника. Проблема використання ТЗН має два аспекти:

1)                     педагогічний – це питання, пов’язані із створенням засобів навчання (створення навчальних відеофільмів, кодопосібників тощо) відповідно до дидактичних вимог навчального процесу, а також із розробкою методики застосування їх у навчально-виховному процесі;

2)                     технічний – це питання, які охоплюють створення потрібної апаратури для демонстрування згаданих вище засобів навчання, яка задовольняла б певні педагогічні й технічні вимоги.

Досвід використання технічних засобів навчання у навчальновиховному процесі показує, що систематичне використання їх поряд з традиційними засобами дає змогу ефективніше розв’язувати дидактичні завдання [92].

Водночас те, що сприймається через почуття на графічні моделі, може бути високо абстрактним за змістом.

І. В. Малафіїк [72, с.104-107] виділяла два види наочності: конкретний (на рівні явищ) і абстрактний (на рівні загального). Конкретна наочність полягає в живому спостереженні реальних об’єктів. Абстрактна наочність характеризує форму вираження логічного знання і сприяє прискоренню мислення людини.

Наочність у процесі засвоєння знань виконує дві основні функції. Перша з них спрямована на розширення чуттєвого досвіду, друга – на розкриття суті процесів і явищ, що вивчаються.

Знаково-символьна наочність реалізує другу функцію. Ефективність використання на уроках математики саме цього виду наочності зумовлена високим рівнем абстракції математичних понять.

Під знаково-символьною наочністю розуміють таку наочність, яка відображає структуру і функцію процесу заміщення, кодування інформації, моделює абстрактні залежності за своїм зовнішнім виглядом і конкретними особливостями через умовно-символьну форму. Існує чотири групи засобів знаково-символьної наочності:

-         функціональна (графіки, формули, рівняння);

-         логіко-генетична (графіки, граф-комплекси);

-         причинно-наслідкова (схеми, таблиці);

-         схематизована (малюнки, діаграми, ескізи, карти, плани) [72, с.110].

Традиційним є використання на уроках математики малюнків, діаграм, схем, таблиць. Ефективність такої роботи значно підвищується, якщо вчитель організовує активну діяльність учнів, використовуючи засоби знаково-символьної наочності.

Вивчення математики неможливо уявити без малюнків. При роботі з малюнками завдання можуть бути такими:

1.     За готовим малюнком (задача, теорема) – розпізнавання об’єктів за їх зображенням (розпізнати поняття; малюнок до теореми; за малюнком сформулювати умови задачі чи визначити її типи) або на основі аналізу декількох малюнків зробити узагальнюючий висновок (висунути гіпотезу).

2.     Самостійне виконання малюнка – зобразити геометричну фігуру за її суттєвими ознаками або виконати малюнок до теореми чи задачі.

Діаграма у перекладі з грецької означає зображення, малюнок, креслення. Але далеко не кожен малюнок можна назвати діаграмою. 

Під діаграмою розуміють умовне зображення, яке унаочнює співвідношення між різними значеннями однієї або кількох змінних (здебільшого – величин). Діаграми як засіб знаково-символьної наочності доцільно використовувати на уроках математики з метою узагальнення і систематизації знань, усвідомлення учнями взаємозв’язків між поняттями, що вивчаються. Однак використання діаграм у процесі навчання математики буде ефективним лише у тому випадку, коли учні вміють їх «читати», тобто розуміють суть взаємозв’язків, що відображені на діаграмах. У цьому плані необхідна підготовча робота вчителя з учнями.

Теоретичні та методичні аспекти використання діаграм у школі набули актуальності та широко висвітлювалися в часи модернізації математичної освіти, коли курс математики будувався на теоретикомножинній основі з активним використанням поняття відношення між різними класами множин та їх елементами (У. Боумен, В. Лисенко, Ж. Піаже, А. Столяр тощо).

Ґрунтовніше ознайомлення   учнів з        діаграмами є        не      просто довантаженням додатковою інформацією, а може суттєво сприяти засвоєнню передбаченого програмою матеріалу.

Діаграми є одним з поширених способів наочного представлення інформації. Вони знаходять застосування в різних галузях людської діяльності – статистиці, економіці, управлінні виробництвом тощо.

Виділяють такі особливості використання діаграм на уроках математики [72]: 

•       роботу з діаграмами необхідно починати на найпростіших прикладах – це означає, що поняття, які розглядаються, повинні бути добре засвоєні учнями;

•       ускладнення роботи з діаграмами може йти шляхом збільшення кількості понять, що розглядаються, і підвищення рівня самостійності виконання учнями завдань.

При роботі з діаграмами активізувати діяльність учнів можна за допомогою таких завдань:

ü доповнити зображення елементами, яких не вистачає;

ü виключити зайві елементи;

ü замінити окремі елементи зображення; ü скоригувати місце окремих елементів.

Одним з традиційних заходів знаково-символьної наочності є таблиці. Особливостями є велика інформативність, а також наочність і стичність  представленої інформації, з метою узагальнення знань учнів, засвоєння понять в системі, ефективним є використання систематизуючих таблиць. Таблиці такого типу можуть заповнювати самі учні під керівництвом вчителя математики. Це можна зробити поступово, протягом декількох уроків або після вивчення цілого розділу. До кожної таблиці вчитель може запропонувати систему питань, що сприяють усвідомленню учнями взаємозв’язків між поняттями [72].

Широке впровадження в навчальний процес нових інформаційних технологій навчання, що базуються на комп’ютерній підтримці навчальнопізнавальної діяльності, відкриває перспективи щодо гуманізації навчального процесу, розширення та поглиблення теоретичної бази знань і надання результатам навчання практичної значущості, інтеграції навчальних процесів і диференціації навчання відповідно до запитів, нахилів та здібностей учнів, інтенсифікації навчального процесу й активізації навчально-пізнавальної діяльності, посилення спілкування учнів і вчителя та учнів між собою, збільшення питомої ваги самостійної навчальної діяльності дослідницького характеру, розкриття творчого потенціалу учнів і вчителів з урахуванням їхніх позицій та вподобань, специфіки перебігу навчального процесу.

При цьому насамперед йдеться про поступове і неантагоністичне, без руйнівних перебудов і реформ, вбудовування нових інформаційних технологій навчання різних навчальних предметів у діючі дидактичні системи, гармонійне поєднання традиційних та комп’ютерно-орієнтованих методичних систем навчання [36].

Нові інформаційні технології навчання надають потужні й універсальні засоби отримання, опрацювання, зберігання, передавання, подання різноманітної інформації, наперед розроблені засоби виконання технічних нетворчих операцій, пов’язаних із дослідженням різних процесів і явищ або моделей, розкривають широкі можливості щодо істотного зменшення навчального навантаження і водночас інтенсифікації навчального процесу, надання навчально-пізнавальній діяльності творчого, дослідницького спрямування, яка природно приваблює дитину і притаманна їй, результати якої приносять учню задоволення, стимулюють бажання працювати і набувати нових знань.

Необхідність якомога ширшого використання нових інформаційних технологій навчання різних навчальних предметів пов’язана перш за все зі значно ширшими (порівняно з традиційними технологіями навчання) можливостями розкриття загальноосвітніх функцій навчальних дисциплін, розв’язання загальних завдань навчання, виховання і розвитку школярів.

Значну роль нові інформаційні технології навчання відіграють у формуванні загальнонаукових умінь та навичок (організаційних, загальнопізнавальних, контрольно-оцінювальних), до яких належать вміння адекватно добирати програмний засіб для розв’язування поставленого завдання і формування та розвиток в учнів потреби неперервно розширювати й поглиблювати свої знання [36].

Попередні намагання організовувати і проводити навчання за допомогою комп’ютерних програм, що здійснювались ще на початку та в середині 80-х років, закінчились невдачею. Це було викликано тим, що недосконалість програмових засобів не дозволяло отримати явну перевагу комп’ютерних технологій перед традиційними формами навчання. Іншою важливою причиною являлось те, що комп’ютер на той час не був доступним засобом навчання. Ні вчителі, ані учні не були готові сприйняти комп’ютер як регулярний навчальний засіб.

На даний момент ситуація змінилась, сучасні персональні комп’ютери і програми дозволяють не тільки організовувати найпростіші тести, але й моделювати навчальні ситуації за допомогою анімації, звуку, фотографічної точності [37].

Розглянемо питання про способи використання комп’ютера у навчанні.

Найприродніша форма роботи вчителя – урок. Урок, на якому в якості технічного засобу навчання використовується комп’ютер, можна називати уроком з комп’ютерною підтримкою (УКП). Такі уроки мають особливу структуру, але теорія УКП, на жаль, ще не розроблена. УКП мають особливі цілі, форми і особливу методику визначення результативності. Головним завданням є організація такого уроку.

Ще одне важливе теоретичне питання: для яких категорій учнів комп’ютерні технології можуть дати найбільший ефект, а для яких використання комп’ютера не приводить до значних змін результатів навчання [37].

Однак використання комп’ютера в навчанні не обмежується уроками з комп’ютерною підтримкою. Уроки навіть не найважливіша частина цього процесу. Реальна перспектива – використання домашнього комп’ютера в якості навчального засобу, самостійна навчальна діяльність, активне втручання вчителя в домашню освіту через персональний комп’ютер при дистанційному навчанні.

Можна виділити позитивні особливості роботи з комп’ютерною навчальною програмою:

Ø  скорочення часу вироблення технічних навичок учнів;

Ø  збільшення кількості тренувальних завдань;

Ø  досягнення оптимального темпу роботи учня;

Ø  перетворення учня на суб’єкт навчання (так як програма вимагає від нього активного управління);

Ø  застосування в навчальній діяльності комп’ютерного моделювання реальних процесів;

Ø  забезпечення навчання матеріалами із віддалених баз даних, використовуючи засоби телекомунікації;

Ø  набуття діалогу з програмою характеру навчальної гри, що у більшості учнів підвищує мотивацію навчальної діяльності [36].

Потрібно також враховувати і недоліки:

ª  відсутність емоційності діалогу з програмою;

ª  програмісти не завжди враховують особливості конкретної групи учнів;

ª  майже повна відсутність розвитку мовлення, графічної та писемної культури учнів;

ª  виникнення, крім помилок у вивченні навчального предмету, яких учень допускається і на традиційних уроках, також технологічних помилок – помилок роботи з комп’ютерною програмою;

ª  подання навчального матеріалу, як правило, в умовній, надто стиснутій та одноманітній формі;

ª  обмеження контролю знань кількома формами – тестами або програмованим опитуванням;

ª  наявність спеціальних знань самого вчителя.

Недоліків у комп’ютерного навчання не менше, ніж переваг. Відмовлятися від комп’ютера в навчанні не можна, але не можна і зловживати комп’ютеризацією. Потрібно виробити критерії корисності використання комп’ютерів на уроці для кожної вікової групи по окремих темах, критерії оцінювання програмових засобів [36].

Зрозуміло, що та чи інша комп’ютерна технологія потрібна, якщо вона дозволяє отримати такі результати навчання, які не можна отримати без її використання. Наприклад, якщо програма дозволяє швидко виробити технічний навик побудови симетричних фігур на площині – така програма потрібна. Тому що без комп’ютера робота буде перевантажена масою додаткових рутинних побудов і найпростіших дії, а через велику кількість додаткових дій важко сформувати і проконтролювати потрібне вміння. Однак пізніше набуті вміння потрібно закріпити реальними побудовами, інакше справжні навички не розвинуться [36].

Які ж особливості комп’ютеризованого уроку? Потрібно виділити наступне: крім звичайної мети уроку, урок з комп’ютерною підтримкою має технологічну мету (навчання новому методу навчальної діяльності, використанню конкретної навчальної комп’ютерної програми). Головною особливістю такого уроку є те, що перевизначаються потоки інформації на уроці – діалог вчителя з учнем відбувається через комп’ютер, який виступає в ролі третього компоненту навчання , індивідуального для кожного учня.

Можна виділити три основні задачі, які необхідно розв’язати для успішного проведення комп’ютеризованого уроку: дидактичну, методичну і організаційну. Під дидактичним забезпеченням розуміють навчальні матеріали уроку, конкретна навчальна програма та апаратура. Методична задача – визначення методів використання комп’ютерів при викладанні теми, аналіз результатів уроку і постановка наступної навчальної мети. Організаційна задача, яка легко вирішується під час традиційного уроку, стає головною. Вона полягає в тому, щоб виробити і закріпити в учнів навички роботи з навчальною програмою та організувати роботу, уникаючи перевантаження учнів і нераціонального використання часу [37].

При використанні навчальних програм потрібно враховувати слабкість комп’ютерного опитування – не прослідковується хід розв’язування задачі, відсутня можливість перевірки графічних навичок і навичок проведення доведень. Отже, не можна вважати комп’ютерні тести переважаючою формою контролю. Однак для багатьох учнів робота з комп’ютерними тестами буде більш значущою, ніж при традиційній формі опитування. До таких дітей відносяться інтелектуально обдаровані діти, які, до того ж часто відчувають серйозні труднощі у спілкуванні із вчителем, що пов’язане із низькою комунікативною культурою. До таких учнів відносяться і невстигаючі учні. Для них не надто складних тест на комп’ютері може стати засобом самоствердження [25].

Постає питання: як ставитися до автоматичного виставлення оцінок учню комп’ютерною програмою? Напевно не треба довіряти цю справу комп’ютеру. Оцінка завжди суб’єктивна. Вона визначається багатьма факторами, в першу чергу, особистими якостями і взаємовідносинами вчителя і учня.

Розглянемо деякі фактори, що найбільше впливають на побудову уроку:

•      методична мета уроку і тип уроку, який нею визначається (пояснення нового матеріалу, закріплення, узагальнення матеріалу, проміжний контроль тощо);

•      кількість учнів у класі і кількість комп’ютерів у навчальному кабінеті;

•      гігієнічні вимоги до роботи учнів за комп’ютером;

•      рівень підготовки класу;

•      готовність учнів до нового виду навчальної діяльності (від того, наскільки учні добре володіють прийомами роботи з комп’ютерними програмами залежить темп і успіх уроку) [25].

Потрібно пам’ятати, що основна перевага, яку комп’ютер дає на уроці, полягає в тому, що учень сам визначає темп своєї роботи з програмою. Під час традиційного уроку вчитель чітко по часу розподіляє етапи уроку і відводить конкретний час на розв’язування кожної задачі. При цьому деякі учні «все виконали, що далі?..», а інші не встигають за вчителем. Намагання таким чином побудувати комп’ютерний урок не дасть можливості реалізувати основну перевагу уроку з комп’ютерною підтримкою. Програма повинна вступити в діалог з кожним учнем, причому інтелектуальний рівень цього діалогу задається вчителем і програмою, а темп та смислові акценти – самим учнем.

Отже, вчитель не може керувати комп’ютерним уроком за допомогою голосу. Вихід із цієї ситуації в тому, що учень отримує програму дій на урок. Ця програма представляє собою хід уроку. Рівень деталізації навчальних етапів та керівництва діями учня залежить від вище викладених факторів. Якщо клас різнорівневий, то можна розробити окремий модуль для кожної підгрупи [36].

Програма дій може бути представленою у різних формах. Для технологічно слабких учнів, які недостатньо добре вміють працювати з комп’ютером, краще запропонувати віддрукований на папері план. Для інших учнів можна підготувати спеціальний файл, який буде переглядатись за допомогою текстового редактора.

На уроках з комп’ютерною підтримкою не слід принижувати значення традиційного робочого зошита. При вивченні будь-якого матеріалу за допомогою комп’ютера потрібні означення, правила, властивості та теореми необхідно записувати в зошит, як на традиційному уроці.

Розглянемо найменш сприятливу ситуацію при підготовці до уроку з комп’ютерною підтримкою: клас, з яким доведеться працювати, неоднорідний за математичною підготовкою і технологічно погано готовий. В такій ситуації урок проводити по новому матеріалу не потрібно. Головною метою такого уроку повинна бути мета технологічна – навчити учнів працювати з потрібною програмою. При цьому для кожної підгрупи можна виділити окрему мету уроку. Отримуємо два-три уроки в одному. Використання комп’ютера дає змогу диференціювати завдання не тільки за рівнем складності, а й за метою уроку.

Клас можна об’єднати у три групи. Кожній групі потрібно підготувати невеличке програмне завдання, яке розраховане на 10-12 хвилин самостійної роботи з комп’ютером. До уроку кожен учень знає номер свого комп’ютера (комп’ютери в класі повинні бути пронумеровані), причому один і той же номер повідомляється трьом учням, що належать до різних підгруп.

З точки зору вчителя урок можна представити у вигляді такої таблиці:

 

 

 

Етап	І підгрупа	ІІ підгрупа	ІІІ підгрупа	Час
1.	Організаційний момент, постановка мети			2 хв.
2.	Робота з комп’ютером	Інші форми роботи	Інші форми роботи	10 хв.
3.	Інші форми роботи	Робота з комп’ютером	Інші форми роботи	10 хв.
4.	Інші форми роботи	Інші форми роботи	Робота з комп’ютером	20 хв.
5.	Підсумки уроку, домашнє завдання			3 хв.

Таким чином, урок складається з п’яти етапів. Організаційний момент і постановка мети тривають однаково для всіх. А ось зміна решти етапів для кожного учня індивідуальна. Учні другої і третьої підгруп знають послідовність своєї роботи за комп’ютером. Як тільки учень першої підгрупи звільнив комп’ютер, за роботу сідає учень другої підгрупи, а потім і третьої. Сильні учні звільняють робоче місце, як правило, раніше. Вчителю доведеться прослідкувати за тим, щоб учні другої групи не затримувались за комп’ютером більше відведеного часу. Зате слабкі учні в результаті такої побудови уроку отримують більше за всіх часу для роботи з комп’ютерною програмою [36].

Така схема побудови уроку з успіхом виправдовує себе. На такому уроці вчитель виступає і якості консультанта, а не в якості «джерела знань».

Якщо в класі є учень, що має міцні знання і навички роботи з комп’ютером, можна використовувати його як технічного консультанта. На цю роль можна запросити вчителя інформатики або старшокласника, якщо є така можливість [36].

Така схема добре зарекомендувала себе під час роботи на уроках математики з використанням програми GRAN.

Не зайвим буде навести приклади деяких програмних засобів, які можна використовувати для проведення уроків з комп’ютерною підтримкою.

У світі існує багато інформаційних засобів (програм) для спрощення складних математичних розрахунків і громіздких геометричних побудов. Складність програм змінюється – від найпростіших навчальних до складних професійних систем [37].

З успіхом можна використовувати не тільки спеціальні математичні програми, а й багато інших, як, наприклад, Microsoft PowerPoint та програм для створення веб-сторінок для подальшого їх перегляду у будь-якому браузері [37].

Для організації перевірки рівня засвоєння учнями навчального матеріалу зручно використовувати навчальний тестовий комплекс UTK-1.52, який можна знайти на сайті www.utk.mastak.ru. До речі, на цьому ж сайті розміщуються і готові тести, які потрібно тільки перекласти українською мовою. 

Впровадження в навчальний процес школи нових інформаційних технологій потребує переосмислення традиційної системи навчання, її змісту, методів і форм організації, залишаючи при цьому незмінними цілі навчання. Це пов’язано з тим, що будь-який засіб (у нашому випадку таким засобом є комп’ютер), включений в ту чи іншу діяльність, впливає на саму діяльність, а особливо тоді, коли йому властиві специфічні, характерні тільки для нього функції. Однак нові інформаційні технології можуть принципово вплинути на процес навчання тільки в тому випадку, коли ці технології будуть включені в нову модель навчання, а їх засоби повною мірою реалізують притаманні тільки їм функції. Основна мета такої моделі навчання – сприяти розвитку учня як особистості, формувати в нього потребу і здібності до дослідницької діяльності, самоосвіти, самовираження та ін. Модель такого навчального процесу повинна базуватися на формулі: діяльність – рефлексія – теоретичні знання і практичні навички. Учень у даній діяльності повинен виступати в ролі активного суб’єкта, а педагог – у ролі організатора комунікацій у тріаді учитель – учень – комп’ютер [36]. 

Якщо розглядати комп’ютер як результат технічного, технологічного досягнення людства в школі, то він виступає тут і як предмет вивчення, і як предмет, який формує навчальне середовище, і як засіб навчальної діяльності. Останній підхід до визначення місця комп’ютера в навчальновиховному процесі все більше поширюється в освітянській громадськості. Ці якості комп’ютера, його властивість виступати у різних іпостасях (залежно від педагогічного завдання та педагогічної ситуації) суттєво відрізняють його від традиційних технічних засобів навчання. Залучення комп’ютера до навчально-виховного процесу – це залучення не тільки техніки, а й того зовнішнього інтелекту, який презентовано через технологію та програмне забезпечення. 

 

          

§3. Аналіз психологічної, дидактичної і методичної літератури  по темі дослідження

Одним з основних завдань, що стоять перед школою, є зміцнення зв’язку навчання з життям. При вивченні математики це насамперед означає, що навчання повинно спиратися на власний життєвий досвід дітей, а педагогічний процес повинен забезпечити найсприятливіші умови для уточнення, систематизації і всебічного збагачення цього досвіду, розвитку інтересу учнів до навчання – одна з важливих проблем удосконалення освіти.

Важливою умовою у здійсненні визначених завдань на уроках математики є раціональне використання вчителем різних засобів наочності. Уміле використання різноманітної наочності у процесі навчання сприяє розвитку самостійності, активності, творчої пізнавальної діяльності, що значною мірою забезпечує підготовку їх до самостійної практичної роботи [123].

Застосування наочності є одним з основних дидактичних принципів навчання. На основні безпосередніх сприймань і міркувань, що спираються на наочність, у дітей спочатку створюється уявлення, а потім формуються поняття. Від якості засвоєння цих початкових понять залежить успіх дальшого засвоєння математики. Дитина розуміє все доступне, наочне, конкретне; вона може запам’ятати певні абстрактні твердження, але, не зміцнені наочністю, вони будуть для неї тільки беззмістовними фразами.

У процесі викладання математики учитель спирається як на безпосереднє сприймання учнями окремих предметів або фактів, так і на їхню уяву. Вона є засобом здобування учнями чуттєвих даних, необхідних для утворення уявлень і понять про предмети чи явища навколишньої дійсності. За допомогою наочності збагачується і розширюється особистий пізнавальний досвід учнів та розвивається спостережливість.

Розвиток абстрактного мислення – одне з основних завдань навчання математики. Під керівництвом учителя учні знаходять загальне в окремих предметах і явищах, відокремлюють істотне від неістотного, головне від другорядного, усвідомлюють зв’язки предметів і явищ. Для розвитку абстрактного мислення важливо створити відповідні умови, однією з яких є цілеспрямоване використання наочності. В оволодінні розумовими операціями (аналіз, синтез, порівняння, абстракція, узагальнення) учням допомагають різні наочні посібники.

У процесі навчання навчальні посібники використовуються порізному: для ознайомлення з новим матеріалом, для закріплення знань, умінь і навичок, для перевірки їхнього засвоєння тощо. Коли наочний посібник виступає як джерело знань, він особливо повинен підкреслювати істотне – те, що є основою для узагальнення, а також показувати неістотне, його другорядне значення. Так, моделі прямокутників треба взяти різних розмірів – це дає можливість дітям побачити, що рівність протилежних сторін є загальна властивість будь-яких прямокутників, вона не залежить від довжини його сторін [123].

Ознайомлюючи з новим матеріалом, вчитель часто використовує наочний посібник для конкретизації нових знань. У цьому разі наочний посібник виступає як ілюстрація словесних пояснень. Наприклад, допомагаючи дітям у пошуках розв’язку задачі, вчитель робить схематичний малюнок або креслення до задачі; пояснюючи прийом обчислення, супроводить пояснення діями з предметами і відповідними записами. При цьому важливо використати наочний посібник своєчасно, ілюструючи суть пояснення, залучаючи до роботи з посібником і пояснення самих учнів. Під час розкриття прийому обчислення, вимірювання, розв’язування задачі тощо треба особливо чітко показувати рух (додати – присунути, відняти - відсунути). Супроводжуючи пояснення малюнком і математичними записами на дошці, вчитель не лише полегшує сприймання матеріалу школярами, а й водночас показує зразок виконання роботи в зошитах. Тому креслення і записи на дошці треба виконувати грамотно, красиво розміщувати їх на дошці і стежити за тим, щоб їх було добре видно всім дітям. Під час ознайомлення з новим матеріалом і особливо під час закріплення юнь і вмінь треба так організовувати роботу з наочними посібниками, щоб учні самі оперували ними і супроводжували свої дії відповідними поясненнями. Якість засвоєння матеріалу в цих випадках значно підвищується, бо в роботу включаються різні аналізатори. При цьому учні не лише опановують математичні знання, а й набувають уміння самостійно виготовляти наочні посібники. Учитель повинен заохочувати школярів до використання наочних засобів під час самостійної роботи [123].

На етапі закріплення знань, умінь і навичок для різноманітних вправ широко використовують довідкові таблиці, таблиці для усної лічби, малюнки, схеми, креслення для складання дітьми задач.

Наочні посібники іноді використовують для перевірки знань і вмінь учнів. Найбільше унаочнення потрібно при вивченні нового матеріалу, при закріпленні і повторенні – лише частково. З невстигаючими учнями такі унаочнення потрібно використовувати частіше.

Неправильно підібране наочне приладдя не допомагатиме, а лише заважатиме роботі – наочні посібники треб вміло використовувати на уроці.

Слід пам’ятати, що унаочнення не самоціль, а засіб навчання: допомагає учням засвоювати математичні поняття, переходити від конкретного сприймання до абстрактного висновку. При надмірному унаочненні робота схожа на гру, учень бавиться, не напружуючи своєї думки. Таке унаочнення втрачає свою доцільність, воно перетворюється у гальмо розумового розвитку учнів. Як відомо, перед вчителем математики стоїть завдання не лише дати учням міцні знання і навички, але й розвинути їхнє мислення, зацікавити у вивченні математики, активізувати їх пізнавальну діяльність, привчити працювати самостійно, щоб, закінчивши школу, вони могли самостійно підвищувати свою кваліфікацію у майбутній трудовій діяльності.

У зв’язку з цим сучасна педагогіка та психологія спрямовують свої зусилля на те, щоб виявити можливості учня, розширити і максимально використати їх для розвитку особистості учня.

За допомогою пізнавальних психічних процесів людина отримує, осмислює і зберігає інформацію про дійсність. У пізнавальній діяльності і сприймання, і пам'ять, і мислення, і уява виступають у єдності. Інформація до людини надходить не як завгодно, а дозується і фільтрується. Цю функцію виконує увага, яка організовує наше пізнання.

К. Д. Ушинський (1824-1871) зазначав: «Увага – це ті єдині двері, через які знання входять у свідомість учнів» [112]. Тому школяр може дивитись – і не бачити, слухати – і не чути, особливо, якщо вчитель неправильно організовує увагу на уроці.

В сучасній психології існує два погляди на місце уваги серед інших психічних явищ [68]:

-           увага – це сторона, аспект будь-якої психічної діяльності (пам’яті, мислення, сприймання тощо) (С.Л. Рубінштейн, М.Ф. Добринін);

-           увага – це самостійний процес, спеціальна діяльність контролю (П.Я.

Гальперін, О.М. Леонтьєв).

Увага        –        це      спрямованість      і         зосередженість    свідомості, які передбачають підвищення рівня сенсорної, інтелектуальної та рухової активності індивіда [33, с.43].

Для підтримки уваги за допомогою інтересу на уроці потрібно дотримуватись таких принципів:

ü змістовний і цікавий виклад матеріалу;

ü розмаїття методів навчання;

ü захопленість і зацікавленість вчителя; ü емоційність уроку.

Закономірності уваги потрібно враховувати і при використанні наочності. Наприклад, вчитель приніс на урок наочність, про яку піде мова через 20 хвилин. Діти ж починають одразу розглядати її, не чекаючи команди і пояснень вчителя – спрацьовує фактор новизни та інтересу. Коли ж мова піде про наочність, увага класу до неї спаде. Тому демонстрування наочності повинно відповідати моменту коментарів і пояснень до неї вчителя [33, с.44].

Від живого споглядання до абстрактного мислення і від нього до практики – такий процес пізнання об’єктивної дійсності. Це значить, що чуттєві процеси – відчуття та сприймання відіграють важливу роль у пізнанні навколишнього світу як його відправний момент. Не менш важливу роль відіграє «живе споглядання» і зокрема сприймання у навчальній діяльності. Слухання мови вчителя, учнів, читання підручника, записів на дошці, використання різноманітних засобів унаочнення – все це, входячи до процесу навчання як його необхідні компоненти, здійснюється шляхом сприймання

[90, с.28].

Сприймання – це психологічний процес відображення в мозку людини предметів та явищ в цілому, у сукупності всіх їх якостей та властивостей при безпосередній дії подразників на аналізатори. Якщо відчуття відображає лише окремі ознаки, то сприймання – предмет у цілому, у взаємозв’язку його ознак і властивостей [33, с.51].

У навчанні беруть участь різні види сприймання: зорове, слухове, дотикове, рухове та ін. 

Б. Г. Ананьєв вважає, що центральне місце серед них належить зоровому сприйманню. Це пояснюється тим, що зоровий рецептор на відмінну від інших, забезпечує цілісне предметне сприймання [39].

У сприйманні велику роль відіграє мова. Ознайомлюючи дітей з тим чи іншим явищем, учитель повинен дбати про правильність і чіткість своєї мови, бо це позначається на якості уявлень, що виникають в учнів.

Мові належить важливе місце в раціональній організації унаочнення в навчальному процесі.

Поєднання вербальних та наочних засобів навчання може мати різний характер. В одних випадках учитель за допомогою словесних пояснень керує спостереженнями учнів, яке має певною мірою самостійний характер. В інших випадках вчитель описує певне явище, дає йому характеристику й ілюструє демонстрацією наочних приладів. Перша форма сполучення слова і спостереження, на думку Л. В. Занкова, більш продуктивна, тому що забезпечує певну самостійність у роботі учнів [42].

Знання закономірностей людської пам’яті необхідне для організації різних видів діяльності. Але важливість врахування цих закономірностей ніде не важить так багато, як у навчанні [90, с.28].

Вітчизняний       психолог    П.Л.М’ясоїд         [80]   наголошує, що використовуючи наочність протягом уроку, вчитель тим самим покращує пам'ять учнів.

Запам’ятовування, збереження і відтворення індивідом його досвіду називають пам’яттю [33, с.54].

Осмисленість і міцність запам’ятовування підвищується, якщо логічна робота над матеріалом спирається на образні зв’язки. Так, при складанні плану матеріалу, який потрібно запам’ятати, дуже корисним є використання чуттєвої опори у вигляді просторових зорових схем, графічних моделей, що відображають структуру запам’ятовуваної системи понять [90, с.49].

Схема може мати різну наочну форму, але чим більший обсяг матеріалу вона охоплює і чим простіша за своєю побудовою, тим ефективніша вона як спосіб запам’ятовування [90, с.51].

Отже, використання наочності в навчальному процесі допомагає розвивати увагу, пам'ять, сприймання тощо.

Оскільки викладання і навчання – це види діяльності, що є інтегрально взаємопов’язаними сторонами процесу навчання, то ми можемо сказати, що дидактика є наукою про навчання, його цілі і зміст, а також про його методи, засоби і організацію.

Принцип наочності навчання припускає перш за все засвоєння тими, що вчаться знань шляхом безпосередніх наглядів за предметами і явищами, шляхом їх плотського сприйняття. Наочність Я.-А. Коменський вважав золотим правилом навчання [60, с.171].

До використання наочності в процесі навчання зверталися ще тоді, коли не існувало писемності і самої школи. В школах стародавніх країн вона мала досить широке розповсюдження. В середині століття, в епоху панування схоластики і догматизму, ідея наочності вважалася недоцільною і її припинили використовувати в педагогічній практиці. Я.-А. Коменський першим ввів застосування наочності як загально педагогічного принципу.

В основі навчання Коменського про наочність лежить сенсуалістичноматеріалістична гносеологія. Для обґрунтування наочності Коменський багато раз застосовував одну фразу: «…нічого не може бути в свідомості, що наперед не було дане у відчутті…». 

Коменський визначав наочність і її значення таким чином [60]:

1)    «…якщо ми бажаємо прищепити тим, що вчаться істинне і міцне знання речей взагалі, потрібно навчати всьому через особистий нагляд і плотський доказ…»;

2)    «…тому школи повинні надавати все власним відчуттям тих, що вчаться так, щоб вони самі бачили, чули, відчували, нюхали, куштували все, що вони можуть і повинні бачити, чути і т.д., вони позбавлять таким чином людську природу від нескінченних неясностей і галюцинацій…»;

3)    те, що потрібно знати про речі, повинно бути «…викладено за допомогою самих речей, тобто повинно, наскільки можливо, виставляти для споглядання, дотику, слухання, нюху і т.п. самі речі, або замінюючи їх зображеннями…»;

4)    «…хто сам одного разу уважно спостерігав анатомію людського тіла, той зрозуміє і запам’ятає все вірніше,ніж якщо він прочитає найобширніші пояснення, не убачивши всього цього своїми очима…».

Тобто звідси видно, що Коменський наочність вважав не тільки принципом повчальним, але і полегшуючим навчання. Для здійснення наочності Коменський вважав необхідним використовувати:

                а)       реальні предмети і безпосередній нагляд за ними;

                б)      коли це неможливо, то моделі і копії предмету;

                в)      картини як зображення предмету або явища.

Він також говорить, що «…буде корисно, щоб все, що звичайно вивчається в кожному класі, чи то теореми і правила, чи образи і емблеми із викладання предмету, зображувалось наочно на стінах тієї ж аудиторії…»

[60, с.269].

Справедливий вислів Горація: «Повільніше проникає в душу те, що сприймається слухом, ніж те, що ми бачимо своїм надійним поглядом і що сприймається нами як глядачами.» [60, с.303]

В. І. Водовозов (1825-1886) заявляв, «наочність потрібна у викладанні кожного предмета, і при цьому наочність в широкому розумінні слова, де ми діємо не на самий зір, а й на інші почуття» [20].

Л. В. Занков у своїх дослідженнях довів необхідність поєднання слова і наочності в навчанні. Тому сьогодні принцип трактується як вимога використання на всіх етапах навчання предметних і словесних засобів наочності, показу конкретних предметів, явищ, процесів, моделей або їх образних відтворень [42].

На посиленні наочності у викладанні математики наполягав наш видатний математик і педагог М. Остроградський [86]. Про це свідчать спогади його учнів і колег, а також аналіз його педагогічних творів.

«Одних очей мало для того, щоб зберегти предмети в пам’яті, необхідно ще, якщо це можливо, використати дотик. Коли дитина виліпить букви з горщикової глини, хай вона дасть їм підсохнути і, потім повторить те, що вона зробила два-три рази за допомогою моделі або за своїми першими спробами , і тоді можна бути певним, що спогад про ці предмети збережеться назавжди в пам’яті. 

Тільки       цим   єдиним       способом    можна         спростити   вивчення геометричних фігур, вивчення географії і космографії, описової геометрії, фізики і механіки.» [86, с.147]

Щоб привести в систему знання учнів, М. Остроградський пропонує в кожній школі виготовляти та використовувати таблиці.

«Використання великих синоптичних таблиць, що висять у школах, може зафіксувати у мозку учнів без усякого напруження пам’яті основи наук і мистецтва.

Було б дуже дорого купляти для школи великі таблиці, що мають формули та описи. Але кожна школа може мати таблиці, зроблені самими учнями під керівництвом викладачів, і ці таблиці є копіями, знятими з готових рисунків і збільшеними в три-чотири рази.» [9, с.153]

Велике значення засобам навчання у педагогічному процесі надавав відомий педагог-методист С. Шорох-Троцький. Саме цим питанням присвячена його робота [118].

І. Скворцов у своїй роботі [98] дає таку класифікацію засобів навчання:

-       прямі засоби навчання: демонстрація (наочність), вправи та задачі, заучування на пам'ять і повторення, екзамени;

-       непрямі засоби навчання: дисципліна з її допоміжними знаряддями (нагороди і покарання) [98, с.201].

Проблемі використання наочних посібників у процесі розв’язання задач узагалі та навчальних математичних зокрема присвячені роботи науковця і співавтора шкільних підручників З. Слєпкань. У своєму посібнику [101] він говорить, що реалізація дидактичного принципу наочності при формуванні понять – необхідна умова, яка забезпечує ефективність навчання.

Психологічний аналіз ролі наочності в навчанні поданий в книзі Богоявленського і Менчинської [12], де підкреслюється, що «при розумінні процесу учіння як аналітико-синтетичної діяльності під наочністю слід розуміти діяльність учня по відношенню до конкретних предметів і явищ. Це той практичний, реальний аналіз, який зображає першу ступінь пізнавальної діяльності і в цьому розумінні передує розумовому аналізу і синтезу, здійснюваному в словесному плані».

Уміле використання комплексу графічних образів в якості єдиного завдання збільшує визначеним чином пропускну здатність мозку, збільшує протікання на цій базі складних логічних роздумів. Пояснення цьому можна знайти хоч б в тому, що зорові канали переробки інформації в сто разів сильніші слухових.

Наочність сприяє утворенню ясних і точних образів сприйняття і представлення, полегшує учням перехід від сприйняття конкретних предметів до сприйняття абстрактних понять про них шляхом виділення і словесного закріплення схожих загальних суттєвих ознак предметів [101, с.47].

Для ефективного використання наочності важливо детально відбирати її, враховувати, який вид наочності найбільш оптимальний, яку функцію він повинен виконувати. Зокрема, треба визначити, чи буде використана наочність при введенні нового поняття, при розв’язуванні задач чи при проведенні практичної роботи. Важливо навчити учнів сприймати засоби наочності (вказуючи на те, що в даному матеріалі потрібно виділити, порівняти, уявно перетворити) – це сприяє усвідомленню сприйняття, активізує мислення, підвищує пізнавальний інтерес учнів [101, с.48].

Г. П. Бевз вважає, що у підвищенні ефективності уроків з математики провідне місце займає раціональне використання наочних посібників та технічних засобів навчання. Проаналізувавши дане твердження можна сказати, що справжнього успіху досягають ті вчителі, які використовують наочні посібники та технічні засоби навчання в комплексі і лише тоді, коли вони справді сприяють розумінню учнями програмного матеріалу, коли заощаджують час та полегшують роботу [7, с.47].

Використанням наочності на уроках цікавляться багато методистів та психологів.

Грохольська А. наголошує, що одним із засобів економії часу є доцільне використання засобів наочності взагалі, таблиць та екранних засобів зокрема. Вона вважає, що найбільш економно і зручно вчителю виготовляти кодопозитиви власними силами, і навіть описує технологію виготовлення кодопозитивів в умовах наявності сучасної техніки ксерокопіювання [26].

Влітку 1997 року вийшов у світ посібник М. І. Жданова [36]. Досі, принаймні в межах навчально-методичної літератури, ще не було аналогів. Це є практично першим принципово новим навчальним посібником, який демонструє шляхи практичного впровадження в навчальний процес нових інформаційних технологій навчання математики. Він переконливо демонструє можливості комп’ютерної підтримки процесів навчання різних навчальних предметів та перетворення на основі комп’ютерних програм розглянутого типу такого предмету, як математики, який традиційно вважається важкодоступним і складним, в «математику для всіх», а розв’язування задач настільки ж доступним і привабливим, як і «просте розглядання малюнків і графічних зображень».

У підручнику Дьяконова [34] описано новий науковий і прикладний напрямок, який виник на стикові математики та інформатики – комп’ютерна математика. В цій книзі описується теорія і застосування ряду нових систем комп’ютерної математики Excel, Derive, MuPAD, MathCAD, Mathematica, Maple V, MATLAB. Це полегшує оптимальний вибір систем і їх інтеграцію з ціллю ефективного розв’язання різних задач. Тисячі простих і зрозумілих прикладів роблять цю книгу цінним практичним посібником і самовчителем з систем комп’ютерної математики. 

Проаналізувавши психологічну літературу по темі дослідження, а саме Дуткевич [33], Дьяченко [35], Дьяконов [34], М’ясоїд [80] та ін., ми

можемо сказати, що наочність є важливим компонентом активізації пізнавальної і навчальної діяльності учнів. Ще античні греки зазначали, що наочність сприяє кращому запам’ятовуванню інформації і швидшому її відтворенню. Наочність допомагає сконцентрувати увагу учнів на головному, конкретному, що дає позитивні результати при перевірці знань. Також, говорячи про увагу, можна сказати, що використання наочності на уроках в школі сприяє виробленню в людини звички віднаходити головне в матеріалі, сприяє більш точній концентрації уваги на конкретній інформації.

Наочність допомагає закріпити в пам’яті учнів певні математичні факти, бо чим краще початкове зорове сприймання, тим довше воно запам’ятовується.

При використанні наочності на уроках покращується мисленнєва діяльність учнів, оскільки вони оперують не простими «сухими» математичними поняттями, а унаочненим матеріалом, який вони краще розуміють.

Використання наочності сприяє розвитку уяви. Не завжди є можливість використати необхідну наочність на уроці, що може ускладнити розуміння нового матеріалу. В таких випадках на допомогу приходить уява. Наприклад, уява часто використовується при розв’язуванні задач з практичним змістом, таких як: визначення амплітуди коливань і т.д.

Проаналізувавши дидактичну літературу (Бевз [113], Водовозов [20], Коменський [60], Остроградський [86], Скворцов [98], Слєпкань [101] тощо), ми сконцентрували свою увагу на такому принципі навчання, як принцип наочності.

Реалізуючи даний принцип, вчитель мусить пам’ятати, що 

ª наочність – не самоціль, а засіб, який повинен забезпечувати розвиток сприймання, мислення, активності і самостійності учнів;

ª поєднання слова і наочності допомагає осмислити спостережуване, зрозуміти зв’язки між фактами і явищами;

ª недоцільно показувати те, що добре відомо учням, достатньо лише створити відповідні уявлення;

ª надмірна наочність приводить до труднощів сприйняття, а завчасне демонстрування наочності знижує увагу учнів.

Однак, проаналізувавши психологічну і дидактичну літературу, можна сміливо стверджувати, що проблема використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії досліджена недостатньо.

Хоча даній темі присвячено багато методичної літератури, на сьогоднішній день не існує досконалого, всеохоплюючого посібника, який розкривав би повністю методику використання різних видів наочностей на уроках геометрії старшої школи, а також відсутній навчальний комплект наочностей, який би забезпечував ефективне засвоєння учнями програмного матеріалу з теми «Взаємне розміщення прямих і площин» в курсі стереометрії.

Спостерігається тенденція до зменшення кількості тижневих годин, які відводяться на вивчення математики в загальноосвітній школі, особливо там, де математик не є профілюючою дисципліною. Зміст програми та вимоги до знань, вмінь і навичок учнів з математики залишаються майже незмінними.

Проведений аналіз свідчить, що в нині діючих підручниках [10, 86] не

використовують методики, яка б забезпечувала проведення уроків з використанням ілюстративного та наочно-навчального матеріалу, тому виникає необхідність у розробці такої методики.

 

          

ІІ. Методика використання наочності при вивченні взаємного розміщення прямих і площин в курсі

стереометрії в загальноосвітніх навчальних закладах різних

типів і у ВНЗ І-ІІ рівнів акредитації §1. Методика використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії в загальноосвітніх навчальних закладах 

Як і в основній школі, геометрія у старшій школі повинна навчати учнів правильному сприйманню навколишнього світу. Але для цього стереометрія має більше можливостей. Йдеться про розвиток логічного мислення, формування просторових уявлень, формування навичок застосування геометрії до розв’язування практичних завдань.

За діючою програмою [88] на курс геометрії у 10 класі припадає 51 год. (І семестр – 32 год., 2 год. на тиждень; ІІ семестр – 19 год., 1 год. на тиждень; резервний час – 6 год.). Вивчення взаємного розміщення прямих і площин в курсі стереометрії відбувається протягом всього навчального року, а саме в темах «Паралельність прямих і площин у просторі» (22 год.) та «Перпендикулярність прямих і площин у просторі» (22 год.). Матеріал вивчається за підручником [86].

Витяг з програми з геометрії (10 клас)

Тема 1. Паралельність прямих і площин у просторі 

-            Взаємне розміщення двох прямих у просторі. Паралельні прямі у просторі.

-            Ознака паралельності прямих.

-            Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини.

-            Взаємне розміщення двох площин. Паралельні площини. Ознака паралельності площин

Тема 2. Перпендикулярність прямих і площин у просторі 

ü    Перпендикулярність прямих у просторі.

ü    Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини.

ü    Перпендикулярні площини. Ознака перпендикулярності площин.

Сучасні комп’ютерні технології дозволяють більш ефективно вивчати окремі теми шкільного курсу математики. 

 

Тема уроку.  Взаємне розміщення двох прямих у просторі. Паралельні прямі у просторі.

Обладнання:  каркасна модель куба, схема «Взаємне розміщення двох прямих у просторі»

Хід уроку

І. Організаційна частина ІІ. Пояснення нового матеріалу

Вчитель. Із курсу планіметрії відомо, що дві прямі, які лежать у площині можуть перетинатися або не мати спільних точок. Сформулюйте означення паралельних прямих на площині.

Учні. Якщо дві прямі лежать в одній площині і не мають спільних точок, то вони називаються паралельними.

Вчитель. У просторі дві різні прямі або перетинаються, або не перетинаються. Перший випадок дає зрозуміти, що прямі лежать в одній площині. Проте другий випадок допускає дві можливості: прямі лежать в одній площині або ж вони належать різним площинам. 

Означення. Прямі, які лежать в одній площині і не перетинаються, називаються паралельними. А дві прямі, які не лежать в одній площині, називаються мимобіжними.

(Випадки взаємного розташування двох прямих у просторі доцільно демонструвати за допомогою каркасної моделі куба, ребра якого вважаючи прямими у просторі.)

Вчитель. Отже, дві прямі  а  і  b у просторі можуть: перетинатися, бути паралельними, бути мимобіжними (схема «Взаємне розміщення двох прямих у просторі»).

 

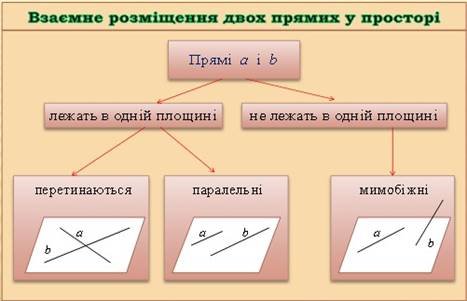
Вчитель. Пригадаємо аксіому ІХ з курсу планіметрії, яка вважається основною властивістю паралельних прямих.

Учні. Через точку, що не лежить на даній прямій, можна провести на площині пряму, паралельну даній, і до того ж тільки одну.

Вчитель. З цієї аксіоми паралельності випливає, що на площині через дану точку можна провести не більше однієї прямої, яка паралельна даній прямій. Давайте з’ясуємо, скільки таких прямих можна провести у просторі.

Нехай дано пряму а і точку А, що не лежить на ній (мал. 1).

 

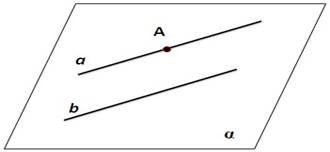
Мал. 1

Через них можна провести площину α (за теоремою 1.1). У цій площині можна провести пряму b, яка буде паралельною до даної прямої а.

Отже, у просторі через дану точку А можна провести пряму, паралельну прямій  а.

Таким чином, справедлива теорема (формулюють учні):

Теорема 2.1. Через точку, яка не лежить на даній прямій, можна провести пряму паралельну даній, і тільки одну.

Доведення.

Самостійна робота з підручником (ст. 11).

Запитання до класу

1.            Як треба розуміти, що дві прямі у просторі не паралельні?

2.            Що можна сказати про прямі у просторі, якщо відомо, що вони не мимобіжні?

3.            Як формулюється теорема 2.1 ? ІІІ. Закріплення набутих знань

№ 3. Доведіть, що всі прямі, які перетинають дві дані паралельні прямі, лежать в одній площині.

Доведення.

Учні розбирають за підручником. (ст. 10)

№ 5(4). Через кінці відрізка АВ і його середину М проведено паралельні прямі, що перетинають деяку площину в точках А₁, В₁ і М₁. Знайдіть довжину відрізка  ММ₁ , якщо відрізок АВ не перетинає цю площину і відомо, що АА₁ = а,  ВВ₁ = b. 

№ 7 (1). Через кінець А відрізка АВ проведено площину. Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетинають площину в точках  В₁ і С₁. Знайдіть довжину відрізка  ВВ₁ , якщо СС₁=15 см, АС:ВС = 2:3.

IV. Домашнє завдання

§2, п. 7;  контрольні запитання №3; задачі № 5 (2), 7 (4) (ст. 18-19)

V. Підведення підсумків уроку

1.  Як можуть розташовуватись дві прямі у просторі?

2.  Які прямі називаються паралельними?

 

Тема уроку.        Ознака паралельності прямих.

Обладнання:      моделі прямокутного паралелепіпеда і куба, кодопозитив.

Хід уроку

І.  Перевірка домашнього  завдання.  Актуалізація опорних знань учнів

Два учні біля дошки виконують рисунки до задач №5(2) і №7(4) та відтворюють основні моменти розв’язання.

Запитання до класу

1.                       Скільки прямих, паралельних даній прямій, можна провести у просторі через точку:

а) яка не лежить на даній прямій?

б) яка належить даній прямій?

2.                       Сформулюйте ознаки паралельності прямих на площині.

ІІ. Пояснення нового матеріалу

В планіметрії вивчались три ознаки паралельності прямих на площині: 

-           Якщо внутрішні різносторонні кути рівні, то прямі паралельні; 

-           Якщо сума внутрішніх односторонніх кутів дорівнює 180^о, то прямі паралельні;

-           Дві прямі, які паралельні третій, паралельні одна одній.

Перші дві ознаки паралельності не мають аналогів для прямих у просторі. Остання ж ознака справедлива і в стереометрії.

Сформулюємо її.

Теорема 2.2. Дві прямі, паралельні третій, паралельні між собою.

Доведення.

Доводить спочатку вчитель сам, а потім повторює разом з учнями, відповідно до тексту підручника.

ІІІ. Закріплення теоретичного матеріалу

1.            Дано зображення куба. Доведіть, що AA₁ || СС₁ .

Доведення.

Зобразимо даний куб і позначимо його вершини (мал. 2).

 

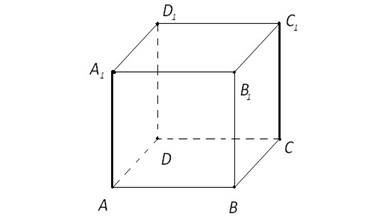
Мал. 2

Розглянемо квадрат  АА₁ВВ₁ : його сторони АА₁ і ВВ₁ паралельні. 

Аналогічно, у квадрата ВВ₁СС₁ паралельними будуть сторони ВВ₁ і

СС₁. З того, що АА₁ || ВВ₁ та  ВВ₁ || СС₁ випливає, що АА₁ || СС₁ (за теоремою 2.2).

2.            Прямі а і b паралельні, але прямі b та с не паралельні. Доведіть, що прямі а і с не паралельні.

3.            №11 (ст. 19). Доведіть, що середини сторін просторового чотирикутника є вершинами паралелограма (вершини просторового чотирикутника не лежать в одній площині).

Доведення.

 

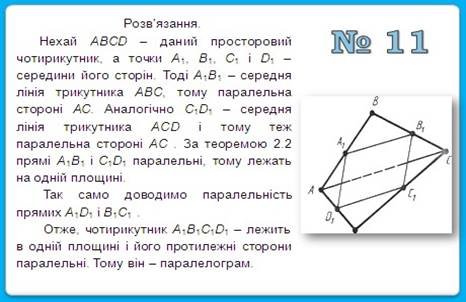
Мал. 3

Дана задача розв’язана в підручнику, проте саме розв’язання і зображення просторового чотирикутника знаходяться на різних сторонах аркуша книги, що приводить до певних незручностей. Тому доцільно запропонувати учням розібратись в ході розв’язання за допомогою наступного кодопозитива (мал. 3).

IV. Домашнє завдання

§2, п. 8;  контрольне запитання №4; задача № 9 (ст. 19)

V. Підведення підсумків уроку

1.  Сформулюйте ознаки паралельності прямих на площині.

2.  Сформулюйте ознаку паралельності у просторі.

 

Тема уроку.        Розміщення          прямої        і         площини     у        просторі. Ознака паралельності прямої і площини.

Обладнання:                 моделі куба і тетраедра, схема «Взаємне розміщення

прямої і площини», кодопозитиви. Хід уроку

І.  Актуалізація опорних знань учнів

1.     Згадайте і сформулюйте теорему про належність площині прямої, дві точки якої належать площині.

2.     Як можуть розміщуватись пряма і площина в просторі?

При обговоренні цього питання доцільно скористатись такою схемою

(мал. 1).

 

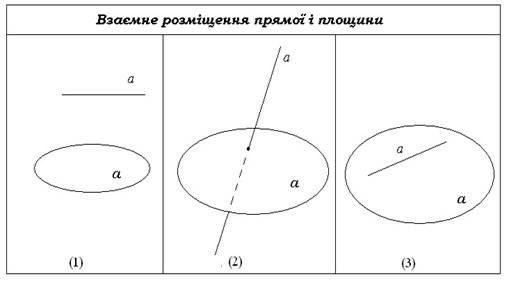
Мал. 1

ІІ. Пояснення нового матеріалу

За частиною (1) схеми можемо сказати, якщо пряма і площина не мають спільних точок, то вони паралельні.

Означення. Пряма і площина називаються паралельними, якщо вони не перетинаються.

Паралельність прямої а і площини α позначається так:  а || α. Наочним представленням прямої, яка паралельна площині, є лінії перетину стіни і стелі – ці лінії паралельні площині підлоги. Відрізок називається паралельним площині, якщо він є частиною прямої, паралельної площині.

Доведемо ознаку паралельності прямої і площини.

Теорема 2.3. Якщо пряма, яка не належить площині, паралельна якійнебудь прямій у цій площині, то вона паралельна і самій площині.  (Доведення записується на дошці і в зошиті.) Дано:  а || b,   bα.

Довести:  а || α .

Доведення.

Припустимо, що пряма а перетинає площину α , тобто пряма і площина мають спільну точку А. 

Якщо Аb, то а і b мають спільну точку А, що суперечить умові. Якщо ж Аb, то прямі а і b мимобіжні, що знову суперечить умові.

Отже, припущення хибне, а тому а || α.

ІІІ. Розв’язування задач Задача 1.

 

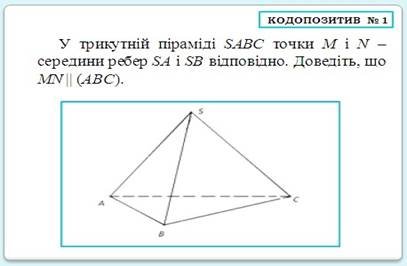
Задача 2.

 

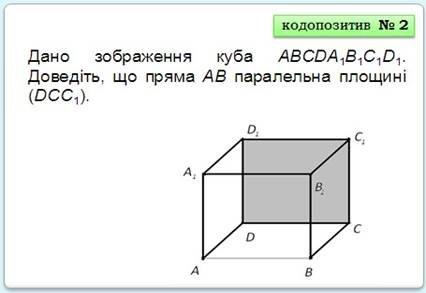
№13 (1) (ст. 19). Дано трикутник АВС. Площина, паралельна прямій АВ, перетинає сторону АС цього трикутника в точці А₁, а сторону ВС – в точці В₁.Знайдіть довжину відрізка А₁В₁, якщо АВ=15 см, АА₁ : АС = 2 : 3.

Розв’язання.

Нехай площина α паралельна прямій АВ і перетинає площину (АВС) по прямій А₁В₁ (мал. 2).

 

Мал. 2

Прямі АВ і А₁В₁ лежать в одній площині (АВС) і не мають спільних точок. Отже, за означенням, АВ || А₁В₁. 

∆АВС ~ ∆А₁В₁С₁, оскільки пряма, паралельна стороні трикутника, відтинає подібний трикутник. 

З умовою задачі маємо:  АВ = 15 см,  АА₁ : АС = 2 : 3.

Нехай  х – коефіцієнт пропорційності, тоді  АА₁ = 2х,  АС = 3х, А₁С=АС – АА₁ = 3х – 2х.

З подібності трикутників:

                       AB         AC                      AB 3x                                     AB 15

                                              або                  3  A₁B₁                     5(см).

                      A1B1               A1C                 A1B1              x                                  3        3

Отже, А₁В₁ = 5 см.

IV. Домашнє завдання

§2, п. 9;  контрольне запитання №5, 6; задача № 14, 15 (ст. 19)

№14. Через дану точку проведіть пряму, паралельну кожній з двох даних площин, які перетинаються.

№ 15. Доведіть, що коли площина перетинає одну з двох паралельних прямих, то вона перетинає й другу пряму.

Доведення. Робота з підручником (ст.12-13).

 

 

 

Тема уроку.  Взаємне розміщення двох площин у просторі. Паралельні площини. Ознака паралельності площин.

Обладнання:      моделі         куба   і         прямокутного      паралелепіпеда,   схема «Взаємне розміщення двох площин», кодопозитиви. Хід уроку

І. Актуалізація опорних знань учнів

ü Що означає : пряма і площина паралельні?

ü Сформулюйте аксіоми стереометрії.

ü Що є перетином двох площин?

ІІ. Пояснення нового матеріалу

Ми знаємо, якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку (аксіома С₂). Звідси випливає, що дві площини або перетинаються по прямій, або не перетинаються, тобто не мають спільних точок (демонструємо схему ).

 

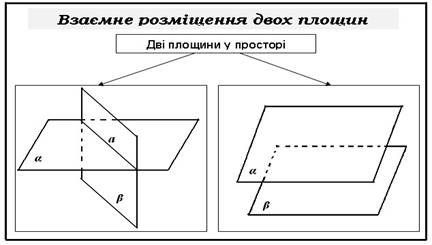
Означення. Дві площини називаються паралельними, якщо вони не перетинаються.

Уявлення про паралельні площини дають підлога і стеля кімнати, дві протилежні стіни тощо.

Якщо площини α і β паралельні, то це позначається так:  α || β.

Завдання. 

1.          На моделях куба і прямокутного паралелепіпеда покажіть паралельні площини і площини, що перетинаються.

2.          Користуючись зображенням прямокутного паралелепіпеда (мал. 1), вкажіть:

а) грані, які перетинають грань ABCD;

б) площини, які паралельні площині (ABC).

 

                                                   Мал. 1

Доводиться ознака паралельності площин згідно з підручником.

Теорема 2.3. Якщо дві прямі, які перетинаються, однієї площини відповідно паралельні двом прямим другої площини, то ці площини паралельні.

Дано: а₁  α ;     а₂  α ;     а₁  а₂ = А;    b₁  β;     b₂  β;    а₁ || b₁;     а₂ || b₂  (мал. 2).

Довести:  α || β.

Доведення.

 

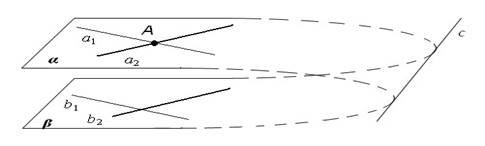
Мал. 2

Припустимо, що α і β перетинаються по деякій прямій с. Оскільки а₁ || b₁, то   а₁ || β, звідси   а₁ || с. Оскільки  а₂ || b₂,  то й  а₂ || β, а тому  маємо  а₂ || с. 

Через точку А проходять дві прямі  а₁  і  а₂ , які паралельні прямій с, що суперечить аксіомі паралельності. Отже, α || β.

ІІІ. Закріплення теоретичного матеріалу

1.          Відомо, що дві прямі, які лежать у площині α, паралельні двом прямим площини β. Чи випливає з цього, що α || β ?

2.          Дано куб ABCDA₁B₁C₁D₁. Доведіть, що: 

а)  ABC || А₁B₁C₁ б)  AB₁D₁ || BDC₁.

3.          Точка В лежить поза площиною α. Проведіть через цю точку площину, паралельну площині α.

4.          № 20 (ст. 19). Через дану точку простору проведіть пряму, яка перетинає кожну з двох мимобіжних прямих. Чи завжди це можливо? IV. Домашнє завдання

§2, п. 10;  контрольні запитання №7, 8; задача № 18, 19 (ст. 19)

№18. Доведіть, що коли пряма перетинає одну з двох паралельних площин, то вона перетинає й другу.

№19. Доведіть, що через дві мимобіжні прямі можна провести паралельні площини.

V. Підведення підсумків уроку

1.  Як можуть розташовуватись дві площини у просторі?

2.  Сформулюйте ознаку паралельності площин.

 

Тема уроку.        Перпендикулярність прямих у просторі

Обладнання:      стереометричний         набір,          таблиця     «Теорема    3.1», кодопозитив.

Хід уроку

І.  Актуалізація опорних знань

1.     Сформулюйте означення перпендикулярних прямих на площині.

2.     Згадайте аксіоми стереометрії.

3.     Сформулюйте ознаки паралельності в просторі.

ІІ. Пояснення нового матеріалу

Поряд з відношенням паралельності в геометрії важливе значення має відношення перпендикулярності. У планіметрії ми говорили про перпендикулярність прямих. Як вже згадувалось, на площині перпендикулярними називаються прямі, які перетинаються під прямим кутом.

У стереометрії розглядається три випадки перпендикулярності:

-                перпендикулярність прямих;

-                перпендикулярність прямої і площини; -    перпендикулярність площин.

На наступних уроках ми займемось послідовним вивченням вказаних випадків , і почнемо з випадку перпендикулярності прямих у просторі.

Означення. Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.

Завдання 1. Назвіть в оточенні моделі перпендикулярних прямих.

Завдання 2. Дано зображення куба. Вкажіть ребра, які будуть перпендикулярними до прямої АА₁.

Завдання 3. Задача №3 (1) з підручника (с. 34).

Вчитель. Що можна стверджувати про взаємне розташування прямих 

а₁ і  b₁, якщо  а || а₁,   b || b₁ і    а  b?

Учні висувають гіпотезу, що  а₁  b. Для ілюстрації доцільно використати каркасну модель куба або прямокутного паралелепіпеда.

Далі формулюється теорема.

Теорема 3.1. Якщо дві прямі, які перетинаються, паралельні відповідно двом перпендикулярним прямим, то вони теж перпендикулярні.

 

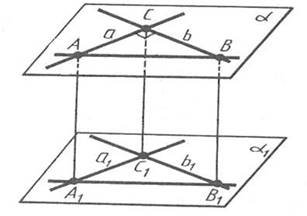
                                                            Мал. 1

Дано:  а  b,   а  α,   b  α;    а₁ || а ,   b₁ || b ,   а₁  α₁ ,   b₁  α₁ , а₁ і   b₁ перетинаються (мал. 1).

Довести:  а₁  b₁ .

Доведення.

Таблиця   «ТЕОРЕМА 3.1»

№ п/п	Твердження	Аргумент
1.	а і b лежать в α, а1 і b1 лежать в α1	Аксіома С3
2.	α || α1	Теорема 2.4
3.	Нехай С – точка перетину а і b, а С1 – точка перетину а1 і b1	Означення
4.	АА1 || СС1, ВВ1 || СС1	Теорема 2.1
5.	АА1 || ВВ1	Теорема 2.2
6.	САА1С1 і СВВ1С1 – паралелограми, тому АС = А1С1, ВС = В1С1	АС || А1С1, АА1 || СС1, ВС || В1С1, ВВ1 || СС1
7.	АА1В1В – паралелограм, тому АВ = А1В1	АВ || А1В1, АА1 || ВВ1
8.	∆АВС = ∆А1В1С1, тому кути А1С1В1 і АСВ рівні і дорівнюють 90о; отже, а1  b1	Третя ознака рівності трикутників

ІІІ. Розв’язування задач

1.            №1 (ст. 34). Доведіть, що через будь-яку точку прямої у просторі можна провести перпендикулярну до неї пряму.

2.            Задача з кодопозитива.

 

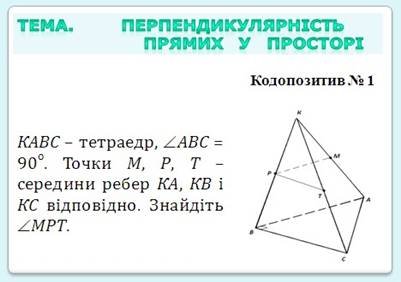
3.            №2 (ст. 34). Доведіть, що через будь-яку точку прямої у просторі можна провести дві різні перпендикулярні прямі.

IV. Домашнє завдання

§3, п. 14; контрольні запитання №1, 2; задача № 3(2, 3) (ст. 34).

№3. Прямі АВ, АС і AD попарно перпендикулярні. Знайдіть відрізок СD, якщо :

2) ВD = 9 см, ВС = 16 см, АD = 5 см; 3) АВ = b , ВС = а , АD = d.

V. Підсумки уроку

1.           Які прямі в просторі називаються перпендикулярними?

2.           Чи визначають площину дві перпендикулярні прямі? Чому?

3.           Сформулюйте теорему 3.1.

 

Тема уроку.        Перпендикулярність      прямої        і         площини.    Ознака перпендикулярності прямої і площини

Обладнання:      модель куба, кодопозитиви, стереометричний набір.

Хід уроку І.  Актуалізація опорних знань учнів ü     Сформулюйте аксіоми стереометрії. 

ü   Які прямі простору називаються перпендикулярними?

ü   Сформулюйте означення паралельних прямої і площини.

ІІ. Пояснення нового матеріалу

Вчитель. Уявлення про пряму, перпендикулярну до площини дають вертикально поставлені стовпи – вони перпендикулярні до поверхні землі чи до будь-якої прямої цієї поверхні, яка проходить через основу стовпа. 

Означення. Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину і перпендикулярна до будь-якої прямої, що лежить у цій площині і проходить через точку перетину.

На мал. 1 пряма с перпендикулярна до

площини  α. Записується це так:  с  α.

З означення випливає, що с  а  і  с  b, де  а, b  α.

 

                            Мал. 1                 

Завдання 1. Укажіть в оточуючому середовищі моделі прямих і площин, які перпендикулярні.

Завдання 2. Що означає твердження: пряма не перпендикулярна до площини?

Завдання 3. Чи правильно, що коли пряма не перпендикулярна до площини, то вона не перпендикулярна ні до жодної прямої, яка лежить в цій площині.

Вчитель. Як перевірити, чи перпендикулярна дана пряма до даної площини? Це питання має практичне значення, наприклад, при установці щогл, колон тощо, які потрібно поставити прямо, тобто перпендикулярно до поверхні землі.

Насправді немає необхідності перевіряти перпендикулярність прямої до всіх прямих, що лежать у даній площині  й проходять через точку перетину даної прямої і площини. 

Відповідь на це питання дає наступна теорема, що виражає ознаку перпендикулярності прямої і площини.

Теорема 3.2. Якщо пряма перпендикулярна до двох прямих, які лежать у площині і перетинаються, то вона перпендикулярна до даної площини.

Доведення.

 

                                                                  Мал. 2

Учні знайомляться з ходом доведення теореми у підручнику.

Незрозумілі моменти вчитель пояснює, використовуючи мал. 2. ІІІ. Закріплення набутих знань

 Дано зображення куба АВСDА₁В₁С₁D₁. Довести, що:

             а) АВ₁С₁D - прямокутник;                          б) В₁D₁  (А₁С₁С).

 Задача з кодопозитива.

Кодопозитив № 1

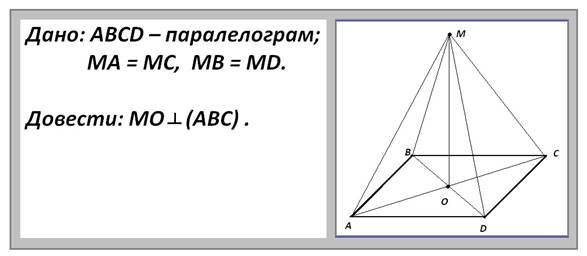
 №6. Центр описаного навколо трикутника кола проведено пряму, перпендикулярну до площини трикутника. Доведіть, що кожна точка цієї прямої рівновіддалена від вершин трикутника (мал. 3).

                                                             

Мал. 3

IV. Домашнє завдання

§3, п. 15;  контрольні запитання №3, 4; задача № 5 (ст. 34).

№5. Доведіть, що через точку, яка не лежить на даній площині, не можна провести більш як одну пряму, перпендикулярну до площини. V. Підведення підсумків уроку

Ø   Яка пряма називається перпендикулярною до площини?

Ø   Сформулюйте ознаку перпендикулярності прямої і площини.

 

Тема уроку.        Перпендикулярні площини. Ознака перпендикулярності площин

Обладнання:      кодопозитиви, стереометричний набір, моделі куба і прямокутного паралелепіпеда. Хід уроку

І. Актуалізація опорних знань учнів Запитання фронтального опитування:

ü   Сформулюйте аксіоми стереометрії.

ü   Які прямі в просторі називаються перпендикулярними?

ü   Сформулюйте ознаку перпендикулярності прямої і площини.

ІІ. Сприйняття нового матеріалу

Означення.        Дві    площини,    що     перетинаються,    називаються перпендикулярними, якщо третя площина, яка перпендикулярна до прямої перетину цих площин, перетинає їх по перпендикулярних прямих.

 

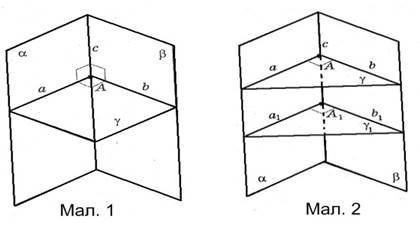
На мал. 1   α  β, бо ці площини перетинаються по прямій с, а

площина  γ, перпендикулярна до прямої  с, перетинає α і β по прямих  а і b, які перпендикулярні.

Означення перпендикулярності площин не залежить від вибору площини γ. Дійсно, візьмемо іншу площину γ₁, перпендикулярну до прямої с (мал. 2).

Оскільки с  γ  та прямі а і b лежать у площині  γ  і перетинаються в точці А, то  с  а,  с  b (за означенням перпендикулярності прямої і площини).

Аналогічно с  а₁, с  b₁. Крім того, прямі  а і а₁  та  b і b₁ лежать відповідно в площинах α і β. Значить а || а₁ та  b || b₁. 

Оскільки а  b,  а || а₁  і  b || b₁, то Значить а₁  b₁ (за теоремою 3.1). ІІІ. Закріплення набутих знань

1.      Наведіть приклади моделей перпендикулярних площин із оточуючого середовища.

2.      Покажіть на моделі прямокутного паралелепіпеда перпендикулярні грані (площини).

3.      №59. З точок А і В, які лежать у двох перпендикулярних площинах, опущено перпендикуляри АС і ВD на пряму перетину площин.

Знайдіть довжину відрізка АВ, якщо АС = = 6 м, ВD = 7 м, СD = 6 м.

Вчитель.   На практиці для   спрощення процедури визначення перпендикулярності площин використовують наступну теорему.

Теорема 3.6. Якщо площина проходить через пряму, перпендикулярну до другої площини, то ці площини перпендикулярні.

Доведення.

Використовуємо кодопозитив №2.

 

ІІІ. Закріплення нових знань

1.     Як на практиці встановити, чи перпендикулярна площина стіни до площини підлоги?

2.     № 54 (с. 38). Дано пряму а і площину α. Проведіть через пряму а площину, перпендикулярну до площини α.

Розв’язання.

Робота з підручником (с. 31).

3.     № 55 (с. 38). Дано пряму а і площину α. Доведіть, що всі прямі, які перпендикулярні до площини α і перетинають пряму а, лежать в одній площині, перпендикулярній до площини α.  

Розв’язання.

Проведемо довільні прямі т  α  і п  α, що перетинають пряму а в точках М і N відповідно (мал. 3). 

За властивістю прямих, перпендикулярних до однієї площини, прямі т і п паралельні. Це означає, що через ці прямі можна провести площину β,

причому β  α (за теоремою 3.6).

 

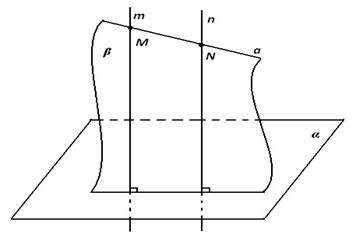
                                                        Мал. 3

Оскільки точки М і N лежать у площині β, то пряма а також лежить у цій площині. Таким чином, усі прямі, що перетинають пряму а і перпендикулярні до площини α, лежать у площині β.

4.     № 61 (с. 39). Площини α і β перпендикулярні. У площині α взято точку А, відстань від якої до прямої с (лінії перетину площин) дорівнює 0,5 м. У площині β проведено пряму b, яка паралельна прямій с і віддалена від неї на 1,2 м. Знайдіть відстань від точки А до прямої b.

IV. Домашнє завдання

п. 20 із §3;  контрольні запитання 11-12; задачі  № 59(2,4,6) (с. 39).

№59. З точок А і В, які лежать у двох перпендикулярних площинах, опущено перпендикуляри АС і ВD на пряму перетину площин. Знайдіть довжину відрізка АВ, якщо:

2) АС = 3 м, ВD = 4 м, СD = = 12 м;  

4) АD = ВС = 5 м,  СD=1 м; 

6) АD = а, ВС = b, СD = с.

V. Підведення підсумків уроку

•      Які площини називаються перпендикулярними?

•      Сформулюйте ознаку перпендикулярності площин.

•      Дано куб АВСDА₁В₁С₁D₁. Враховуючи, що ребра куба, що виходять з однієї вершини, попарно перпендикулярні, укажіть серед наведених тверджень правильні:

а) (АD₁С)  (АD₁D);

б) (АD₁С)  (СDD₁);

в) (АD₁С)  (АDС);

г) (АDD₁)  (АDС).

 

 

Шкільна практика і дослідження психологів, дидактів та методистів свідчать про те, що найбільша потреба в унаочненні виникає у процесі навчання учнів, у яких переважає наочно-дійове і наочно-образне мислення. У старшокласників ця потреба зменшується завдяки розвитку абстрактного мислення. Проте і в них часто виникають труднощі, коли потрібно уявити чіткі образи тих чи інших об’єктів. Тому ці образи спочатку потрібно створити, а лише потім переходити до введення формальних означень відповідних понять і до вивчення їх властивостей. Чим абстрактніше поняття, що вводиться, тим більшої конкретизації потребує його засвоєння. Значну допомогу тут надає правильне й своєчасне використання наочності. При засвоєнні знань, яке відбувається під час практичного аналізу об’єктів (засобів унаочнення), відбувається абстрагування та узагальнення, причому ці розумові дії знаходять опору в наочному матеріалі.

Такий спосіб унаочнення дає змогу учням краще усвідомлювати навчальний матеріал, розвивається образне мислення. Завдяки доцільному використанню того чи іншого засобу унаочнення в учнів формуються та систематизуються знання про основні поняття і аксіоми стереометрії, а також вміння встановлювати взаємне розміщення прямих і площин у просторі, розвиваються вміння обчислювати відстані і кути між прямими і площинами у просторі.

          

§2. Методика використання наочності при вивченні взаємного

розміщення прямих і площин в курсі стереометрії в загальноосвітніх навчальних закладах з поглибленим вивченням математики

У процесі поглибленого вивчення математики в профільних класах основні завдання суттєво доповнюються. Це обумовлено необхідністю виявлення та розвитку в учнів математичних здібностей, формування в них стійких інтересів до математики та професійної діяльності, підготовки учнів до навчання у вищому навчальному закладі освіти.

Навчання у фізико-математичних класах доцільно будувати у відповідності з наступними основними принципами. 

По-перше, вивчення математики у класах відповідного профілю повинно давати учням глибокі математичні знання і широкий математичний розвиток на базі основного курсу математики. 

По-друге, учні-випускники математичних класів повинні володіти такими знаннями і вміннями, які повністю відповідали б вимогам, що пред’являються до математичної підготовки учнів звичайних шкіл, і разом з тим були б більш глибокими і міцними. При цьому отримуваний у процесі навчання математичний розвиток учнів математичного класу повинен давати їм можливість здійснювати творчий підхід до процесу вивчення математики. Учні мають навчитися працювати самостійно з навчальною математичною літературою і мати до закінчення навчання стійкий інтерес до предметів фізико-математичного циклу.

По-третє, у процесі навчання математики у цих класах перед вчителем відкриваються великі можливості у здійсненні оптимальної індивідуалізації навчання, у використанні школярами евристичного методу вивчення математики і проблемної форми навчання, тобто широкі можливості оптимальної активізації навчання. Має широко використовуватись розв’язування нестандартних, конкурсних та проблемних задач, які пропонувались на вступних іспитах до вищих навчальних закладів і входять до програми зовнішнього незалежного оцінювання. А розв’язування задач теоретичного і прикладного змісту у відповідності до програми повинно відбуватися впродовж усього навчального року.

Нарешті, поглиблене навчання математики у старшій школі має відповідати віковим можливостям і потребам школярів.

Навчання в старшій школі у профільному класі з поглибленим вивченням математики передбачає наявність стійкого усвідомленого інтересу до математики та схильності до вибору у майбутньому пов’язаної з нею професії [15].

Результати навчання на цьому етапі мають забезпечувати підготовку старшокласників до продовження освіти у вищому навчальному закладі. Більшість класів з поглибленим вивченням математики створена з метою підготовки до продовження навчання за спеціальностями, які тісно пов’язані з математикою. Тому головний принцип, який визначає математичну підготовку у класах фізико-математичного профілю, – це принцип поступового моделювання професійної діяльності математика.

Основу математичної підготовки у 10-12 класах складають курси стереометрії та алгебри і початків аналізу, які відрізняються від загальноосвітніх не стільки обсягом часу і переліком тем, скільки спрямованістю на реалізацію головного принципу. Повніше реалізувати принцип моделювання професійної діяльності дозволяють курси за вибором та індивідуальні завдання.

Безумовно, що всі змістові лінії традиційного шкільного курсу знаходять у ньому свою реалізацію [7; 9].

Розглянемо орієнтоване тематичне планування основного курсу математики для 10-12 профільних класів фізико-математичного напрямку. Воно розраховане на 480 годин учбового часу відповідно навчального плану для класів цього профілю. При розробці робочої програми слід виходити з часу, що виділяється на предмет в даному навчальному закладі. Орієнтований тематичний план узгоджений з навчальними засобами, що орієнтовані на профільне навчання. Цим планом передбачається сумісне вивчення геометрії та алгебри і початків аналізу. Такий підхід дозволяє якнайкраще розподілити час на вивчення окремих тем, забезпечити природні внутрішні та міжпредметні зв’язки.

Методичні рекомендації надають певну допомогу викладачам щодо розуміння особливостей математичної підготовки для класів даного профілю, а також при виборі різних методичних шляхів і методів викладу навчального матеріалу [89].

Орієнтовне поурочне планування (10 клас)

Тема 1. Паралельність прямих і площин у просторі

Взаємне розташування двох прямих у просторі. Прямі, що перетинаються, паралельні і мимобіжні прямі

Ознака мимобіжності прямих

Ознака паралельності прямих

Взаємне розташування прямої і площини у просторі. Паралельність прямої і площини. Ознака паралельності прямої і площини

Взаємне розташування двох площин у просторі. Паралельність площин

Ознака паралельності площин

Властивості паралельних площин

Тема 2. Перпендикулярність прямих і площин у просторі

Кут між прямими. Перпендикулярність прямих в просторі

Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини

Властивості прямої і площини, перпендикулярних між собою

Теорема про три перпендикуляри

Відстань від точки до прямої. Властивість точки, рівновіддаленої від сторін многокутника

Перпендикулярні площини

Ознака перпендикулярності площин

Розглянемо методику використання наочних посібників при вивченні взаємного розміщення прямих і площин в курсі стереометрії.

Тема уроку.  Взаємне розташування двох прямих у просторі. Прямі, що перетинаються, паралельні і мимобіжні прямі.

Обладнання:      кодопозитиви, стереометричний набір.

Хід уроку

І. Перевірка домашнього завдання

Перевірку правильності виконання домашньої роботи доцільно провести шляхом фронтальної бесіди стосовно задачі на знаходження периметра перерізу. Використовуються при цьому такі запитання:

1.     Поясніть, що таке прямокутний паралелепіпед.

2.     Як побудовано шуканий переріз?

3.     Чому ∆МСК – прямокутний?

4.     Яка довжина ребра СС₁ ?  Чому?

5.     Яка довжина ребра ВС ?

6.     Визначте вид ∆МNК.

7.     Дайте кінцеву відповідь на питання задачі.

ІІ. Сприйняття нового матеріалу

Із курсу планіметрії відомо: якщо дві прямі лежать в одній площині, то вони або перетинаються, або паралельні. 

У стереометрії можливий і третій випадок. Наприклад, якщо АВСD – тетраедр, то прямі АВ і СD не перетинаються і не паралельні. Вони не лежать в одній площині.

Означення. Дві прямі, які не лежать в одній площині, називаються мимобіжними.

На кодопозитиві №1 зображено десятки пар матеріальних моделей мимобіжних прямих.

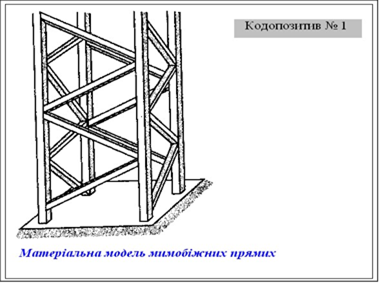
Спочатку розглянемо властивості паралельних прямих у просторі.

Означення. Дві прямі називаються паралельними, якщо вони лежать в одній площині і не перетинаються.

З цього означення випливає, що через дві різні паралельні прямі завжди можна провести площину, і до того ж тільки одну.

Справді, припустимо, що через паралельні прямі а і b проведено дві різні площини, то це означало б, що через пряму а і деяку точку прямої b проведено дві різні площини а це суперечить теоремі 1

Таким чином, маємо ще один спосіб задання площини: площину можна задати двома паралельними прямими. 

Вчитель. Скільки прямих, паралельних даній прямій, можна провести на площині через задану точку?

Учні. За аксіомою ІХ планіметрії (за основною властивістю паралельних прямих) – через точку, що не лежить на даній прямій, можна провести на площині не більш як одну пряму, паралельну даній.

Вчитель. Так, в площині через дану точку можна провести тільки одну пряму, паралельну даній. А скільки таких прямих можна провести в просторі? Відповідь на це питання дає наступна теорема.

Теорема 3. Через будь-яку точку простору, яка не лежить на даній прямій, можна провести пряму, паралельну даній, і до того ж тільки одну.

Дано:           а,    А  а.

Довести:    1)  b, що А b    і  а || b.             2) b – єдина.

Доведення існування.

Твердження	Обґрунтування
Проведемо площину α  {а, А}.	Теорема 1.
Проведемо в площині α через точку А пряму b таку, що b || а.	Основна властивість паралельних прямих.

Доведення єдиності.

Припустимо, що  b₁, яка проходить через точку А і паралельна прямій а. Тоді проведемо через прямі а і b₁ площину β. 

Площина β проходить через пряму а і точку А, що не лежить на ній.

Згідно з єдиністю площини α (за теоремою 1) площини α і β збігаються.

Отже, пряма b, вказана вище, єдина. Теорему доведено.

Вчитель. Дві паралельні прямі завжди лежать в одній площині. А три чи більше? Розглянемо зображення шестерні (кодопозитив №2).

Вчитель. Як бачимо, усі ребра прямозубої циліндричної шестерні лежать на паралельних прямих, але не належать одній площині. То як можна відповісти на наше питання?

Учні. Три чи більше паралельних прямих не обов’язково належать одній площині.

Вчитель. Паралельними бувають не тільки прямі, а й відрізки і промені. Два відрізки або промені називаються паралельними, якщо вони лежать на паралельних прямих.

ІІІ. Закріплення нових знань

Задача. Точки А, В, С і D розміщені так, що АВ || СD. Чи можуть бути мимобіжними прямі АС і ВD?  Чому?

Задача.

 

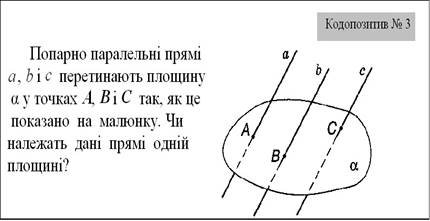
Задача. К, Р, Т, М – середини ребер АВ, АС, CD, DB тетраедра ABCD.

Доведіть, що чотирикутник КРТМ – паралелограм.

Розв’язання (усно).

Використовуємо кодопозитив №4.

 

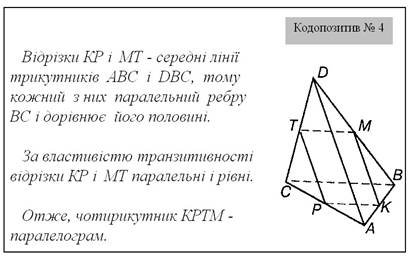
Задача. Знайдіть петиметр чотирикутника КРТМ із попередньої задачі, якщо АD = 6 см, ВС = 8см.

Задача (№58, с. 26). Через кінці відрізка АВ і його середину М проведено паралельні прямі, що перетинають деяку площину в точках А₁, В₁ і М₁. Знайдіть довжину відрізка  ММ₁ , якщо АА₁ = 6,5 м,  ВВ₁ = 8,5 м. 

Розв’язання.

 І випадок: відрізок АВ не перетинає площину. Тоді  АА₁ || ММ₁ || ВВ₁ (за умовою), а тому лежать в одній площині. 

Розглянемо АВВ₁А₁ – це трапеція з основами АА₁  і ВВ₁ та бічними сторонами  АВ  і  А₁В₁ (мал. 1).

 

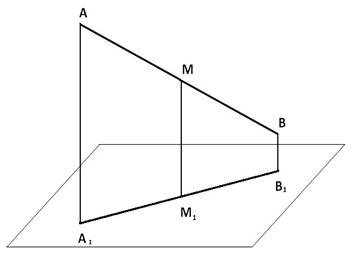
                                                                    Мал. 1

Оскільки АМ=МВ (за умовою задачі), то А₁М₁ = М₁В₁ (згідно з теоремою Фалеса). Тоді ММ₁ – середня лінія трапеції АВВ₁А₁ і дорівнює півсумі її основ, тобто 

аb 6,58,5

                                                                    ММ₁                               7,5 (м)

                                                                                             2              2

Отже, ММ₁ = 7, 5 см.

 ІІ випадок: нехай відрізок АВ перетинає площину в точці О. Оскільки 

АА₁ || ММ₁ || ВВ₁  (за умовою), можна стверджувати, що відрізки  АА₁, ММ₁, ВВ₁ лежать в одній площині β, яка перетинає площину α по прямій

А₁В₁. 

Зобразимо все у площині β. Продовжимо відрізок ММ₁ до перетину з відрізком АВ₁ – дістанемо точку D.

За умовою АМ=МВ, тому АD = DВ₁ (згідно з теоремою Фалеса).

Розглянемо трикутник  АВВ₁: МD – середня лінія, яка дорівнює 

МDBB₁  4,25 (м).

Аналогічно при розгляді середньої лінії М₁D трикутника АА₁В₁ матимемо:

М₁DAA₁  3,25 (м).

Тоді відрізок ММ₁ дорівнює:

_{1                                      1}               BB¹ AA¹                   8,5^6,5            (м).

                                                              ММ MDMD                                        1

₂                                      2

Зауваження. Очевидно, що  АА₁  може бути більшим за   ВВ₁. Тому для загального випадку можна записати:

АА₁ ВВ₁

ММ₁ .

2

IV. Підсумок уроку

1.     Яке розташування прямих у просторі вам відоме?

2.     Які прямі називаються паралельними?

3.     Мимобіжними називаються прямі …

4.     Скільки прямих, паралельних даній прямій, можна провести :

а) через точку, що належить цій прямій;

б) через точку, що не належить цій прямій.

V. Завдання додому

§4; задачі  № 52,  № 57 (с. 25 – 26).

 

Тема уроку.        Ознака мимобіжності прямих.

Обладнання:                 Microsoft PowerPoint, стереометричний набір, моделі

тетраедра і куба.

Хід уроку

І. Мотивація навчальної діяльності

Часто при розв’язуванні задач необхідно з’ясовувати: чи мимобіжні дані прямі? Користуючись означенням мимобіжності прямих, важко відповісти на це питання. Тому на практиці важливу роль відіграє ознака мимобіжності прямих.

ІІ. Усвідомлення нового матеріалу

Сформулюємо і доведемо наступну теорему.

Теорема (ознака мимобіжності прямих). Якщо одна з двох прямих лежить у площині, а друга перетинає цю площину в точці, яка не лежить на першій прямій, то ці прямі мимобіжні.

Доведення.

Учні          розбирають          доведення   ознаки        мимобіжності       прямих, користуючись слайдом № 1, роблять скорочений запис умови та кроків виконання доведення у своїх зошитах. ІІІ. Закріплення нових знань

1.          Дано трикутну піраміду NАВС. Доведіть, що вказані прямі мимобіжні.

                   а)  NС і АВ;                          б) NВ і АС;                     в)  АN і ВС.

2.          Дано куб  АВСDА₁В₁С₁D₁. Доведіть мимобіжність прямих  АВ і СС₁   та   АС₁ і  ВА₁.

3.          Трикутники  АВС  і  АВD  не лежать в одній площині. Доведіть, що прямі  АВ  і  СD  не лежать в одній площині.

4.          Пряма  с  перетинає пряму  а  і не перетинає пряму b, паралельну прямій

а. Доведіть, що прямі  b і с – мимобіжні.

IV. Підсумок уроку

1.     Які прямі називаються мимобіжними?

2.     Сформулюйте ознаку мимобіжності прямих.

V. Завдання додому

§4; розв’язати наступні задачі:

1.                     Через точку А, що не лежить на прямій а, проведено дві прямі, які не мають спільних точок з прямою а. доведіть, що хоча б одна з прямих і пряма а будуть мимобіжними прямими.

2.                     Через вершину А ромба АВСD проведена пряма а, паралельна діагоналі ВD, а через вершину С – пряма b, яка не лежить в площині ромба. Доведіть, що:  а) прямі а і СD перетинаються;  б) прямі а і b

– мимобіжні.

 

Тема уроку.        Ознака паралельності прямих.

Обладнання:  моделі прямокутного паралелепіпеда і куба, кодопозитиви, стереометричний набір.

Хід уроку

І. Актуалізація опорних знань

Проводимо тест на визначення істинності математичних тверджень.

Тест

У просторі дано дві різні прямі а і b, які: варіант 1 – лежать в деякій площині; варіант 2 – не лежать в одній площині.

Позначте символом «+» правильні твердження, символом « – » - неправильні.

1)    Прямі а і b можуть перетинатись.

2)    Прямі а і b можуть бути паралельними.

3)    Прямі а і b можуть бути мимобіжними.

4)    Через пряму а обов’язково можна провести площину, яка перетинає пряму b.

5)    Існує деяка пряма с, яка перетинає і пряму а, і пряму b.

6)    Обов’язково існує пряма с, яка перетинає пряму а і паралельна прямій b.

	1	2	3	4	5	6
Варіант 1	+	+	-	-	+	-
Варіант 2	-	-	+	+	+	+

Відповідь. 

 

 

 

ІІ. Сприйняття нового матеріалу

Як довести паралельність двох прямих на площині? Можна скористатись означенням або ознаками паралельності, тобто теоремами, які дають достатні умови паралельності.

Вчитель. Які ознаки паралельності прямих вам відомі з курсу планіметрії ?

Учні. В планіметрії вивчались три ознаки паралельності прямих на площині: 

-           Якщо внутрішні різносторонні кути рівні, то прямі паралельні; 

-           Якщо сума внутрішніх односторонніх кутів дорівнює 180^о, то прямі паралельні;

-           Дві прямі, паралельні третій, паралельні одна одній.

Вчитель. Перші дві ознаки паралельності не мають аналогів для прямих у просторі. Остання ж ознака справедлива і в стереометрії. Сформулюємо її.

Теорема 4 (ознака паралельності прямих). Дві прямі, паралельні третій, паралельні між собою.

Доведення.

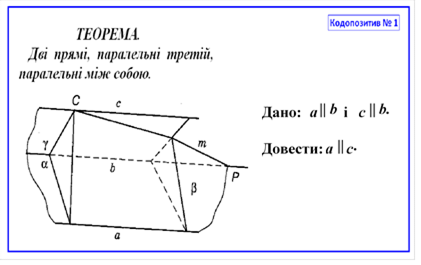
Прямі а і с не можуть перетинатись. Інакше через точку їх перетину проходили б дві різні прямі, паралельні прямій b, що суперечить теоремі 3. 

Припустимо, що прямі а і с мимобіжні (кодопозитив №1). Через паралельні прямі  а і b,  b і с  проведемо площини α і γ, а через пряму а і якунебудь точку С прямої с – площину β.

Нехай площини  γ і β перетинаються по прямій т. Прямі b, с і т лежать в одній площині γ, причому b || с. Тому пряма т, яка перетинає пряму с, буде перетинати в деякій точці Р і пряму b.

Прямі т і b лежать відповідно в площинах β і α. Тому їх спільна точка Р належить цим площинам, а отже, і їх спільній прямій а. Як бачимо, з припущення випливає, що паралельні (за умовою) прямі а і b мають спільну точку Р. Це – суперечність.

Отже, прямі а і с не можуть ні перетинатись, ні бути мимобіжними.

Тому залишається, що а || с.

Вчитель.   Доведену    теорему      називають ще     теоремою   про транзитивність паралельних прямих, оскільки в ній говориться про перехід паралельності прямих двох пар на третю.

ІІІ. Закріплення знань учнів

Задача. Дано зображення куба АВСDА₁В₁С₁D₁ (кодопозитив №2). 

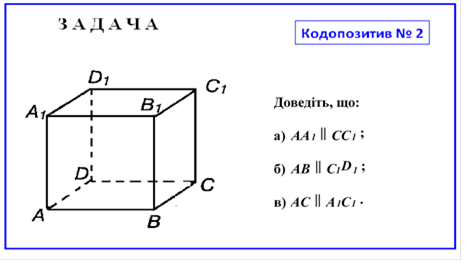
Задача. Чи правильне твердження: якщо прямі b і с не паралельні одній і тій самій прямій а, то вони й не паралельні між собою?

Задача. Трикутник АВС і трапеція АВСD (АВ – основа) не лежать в одній площині. Точки М і N – середини сторін АС і ВС відповідно.

Доведіть, що МN || DС.

Задача. Через кінець А відрізка АВ проведено площину. Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетинають площину в точках  В₁  і  С₁.  Знайдіть довжину відрізка  СС₁, якщо  АС = а,  ВС = b,  ВВ₁ = с.

Задача. Умова задачі на кодопозитиві № 3.

Кодопозитив № 3

З А Д А Ч А

Точка S не лежить у площині АВС, точки М, N, Р – середини відрізків SА, SВ, SС відповідно, точка К лежить на відрізку ВN. Яке взаємне положення прямих: а) NS і АВ; б) РК і ВС; в) МN і

АВ; г) МР і АС; д) КN і АС; е) КМ і АС; є) МS і ВС ? Свою відповідь обґрунтуйте.

 

IV. Підсумок уроку

Аналіз результатів тесту, що виконувався на початку уроку.

V. Завдання додому §4; наступні задачі:

1.                 Нехай О – точка перетину діагоналей паралелограма АВСD, а  α – площина, яка не перетинає паралелограм. Через точки А, В, С, D, О проведено паралельні прямі, які перетинають площину  α в точках А₁, В₁, С₁, D₁, О₁. Доведіть, що:

а)  АА₁  ВВ₁ СС₁  DD₁  4OO₁;

б)  АА₁ СС₁  ВВ₁  DD₁.

2.                 Дано чотири точки А, В, С, D, які не лежать в одній площині. Доведіть, що прямі, які сполучають середини відрізків АВ і СD, АС і

ВD, АD і ВС, перетинаються  в одній точці.

 

Тема уроку.  Взаємне розташування прямої і площини у просторі. Паралельність прямої і площини. Ознака паралельності прямої і площини.

Обладнання:                  кодопозитиви, стереометричний набір, моделі куба і

тетраедра, схема «Взаємне розміщення прямої і площини». Хід уроку

І. Актуалізація опорних знань

1.     Сформулюйте аксіому С₃ (про належність площині прямої, дві точки якої належать цій площині).

2.     Які дві прямі називаються паралельними?

3.     Сформулюйте ознаку паралельності прямих у просторі.

ІІ. Сприйняття нового матеріалу

Вчитель. Ви вже знаєте, що у просторі дві прямі можуть перетинатись, або не перетинатись, тобто бути паралельними (якщо належать одній площині) чи мимобіжними (якщо лежать в різних площинах). Як, на вашу думку, можуть розміщуватись у просторі пряма і площина?

При обговоренні цього питання доцільно скористатись наступною схемою.

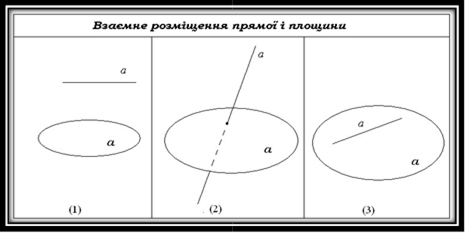
Означення. Пряма і площина називаються паралельними, якщо вони не мають спільних точок.

Вчитель. Паралельність прямої а і площини α позначається так: а || α. Вкажіть в оточуючому середовищі моделі прямих і площин, які паралельні між собою.

Учні. Наприклад, лінії перетину стіни і стелі та площина підлоги паралельні.

Вчитель. Кожне ребро паралелепіпеда паралельне площинам двох його граней (показати на моделі паралелепіпеда). Пряма , проведена в грані бруска за допомогою рейсмуса, паралельна площинам трьох його граней (мал. 1). А також горизонтальні планки мотовила зернозбирального комбайна паралельні площині поля. Усе це – матеріальні моделі паралельності прямої і площини.

 

Мал. 1

Означення. Відрізок називається паралельним площині, якщо він є частиною прямої, паралельної цій площині.

Вчитель. Як для двох прямих у просторі існує ознака паралельності , так і для прямої і площини. Отож, доведемо ознаку паралельності прямої і площини.

Теорема 5 (ознака паралельності прямої і площини). Якщо пряма, яка не лежить у площині, паралельна якій-небудь прямій цієї площини, то вона паралельна і самій площині.

Дано:    а  α,    а || b,     b  α.    

Довести:  b || α.

Доведення.

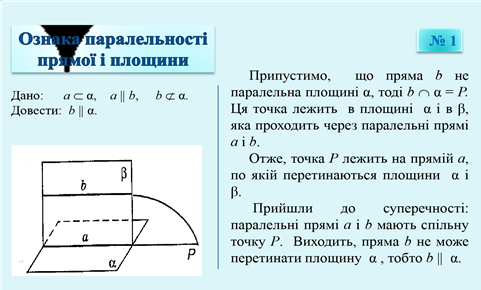
ІІІ. Закріплення набутих знань

Задача.  Кожна з площин α і β паралельна прямій а. Чи можуть ці площини перетинатись?

Задача.  Пряма а перетинає площину α. Скільки можна провести прямих:   1) що перетинають площину α і паралельні прямій а;   2) що перетинають пряму а і паралельні площині α?

Задача.  Площина α перетинає відрізки АВ і АС в їх серединах – точках К і Р. Доведіть, що ВС || α. Як відносяться площі трикутників АВС і АКР ?

Задача. Дано площину α і точку А поза нею. Проведіть через точку А пряму, паралельну площині α.

Вчитель. Які етапи розв’язання задачі на побудову?

Учні. Аналіз, побудова, доведення, дослідження.

Розв’язання.

Доцільно організувати роботу над задачею, використовуючи наступні кодопозитиви (№2, №3, №4). 

За умовою А  а. Щоб пряма а, яка проходить через точку А, була паралельна площині α, достатньо, щоб вона була паралельна прямій b, яка належить площині α.

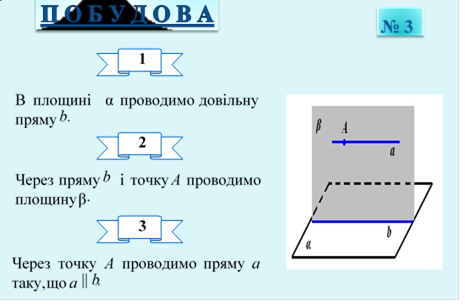
Задача. Дано неплоску замкнену ламану АВСDА. Доведіть, що середини всіх її ланок лежать в одній площині. IV. Підсумок уроку

1.     Як можуть бути розташовані пряма і площина у просторі?

2.     Сформулюйте ознаку паралельності прямої і площини. V. Завдання додому

§5; задачі № 74, № 76, №79 (с. 29 – 30).

 

Тема уроку.        Взаємне     розташування     двох     площин     у     просторі.

Паралельність площин.

Обладнання:      кодопозитиви, стереометричний набір.

Хід уроку

І. Актуалізація опорних знань

Самостійна робота

Варіант 1

1.     Трикутник АВК і трапеція АВСD (АВ || СD) лежать у різних площинах. Доведіть, що пряма СD паралельна площині (АВК).

2.     Пряма а паралельна площині α. Доведіть, що в площині α існує пряма, яка мимобіжна прямій а.

Варіант 2

1.     Дано куб АВСDА₁В₁С₁D₁. Доведіть, що пряма АС паралельна площині А₁С₁D.

2.     Дано мимобіжні прямі а і b. Доведіть, що існує площина, яка містить пряму а і паралельна прямій b.

ІІ. Сприйняття нового матеріалу

Вчитель. Ми знаємо, якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, яка проходить через цю точку (аксіома С₄). Який висновок можна зробити?

Учні. Дві площини або перетинаються по прямій, або не перетинаються, тобто не мають спільних точок.

Означення. Дві площини називаються паралельними, якщо вони не перетинаються.

Якщо площина  α  паралельна площині  β, то  цей  факт записують  так: α || β.

Вчитель. Що в навколишньому середовищі може бути моделлю паралельних площин?

Учні. Наприклад, дві протилежні стіни в кімнаті або стеля і підлога.

Вчитель. А також підлога і поверхня стола, шиби подвійних вікон, протилежні грані цеглини, швелера, двотаврової балки, пилки пилорами тощо (кодопозитив №1).

 

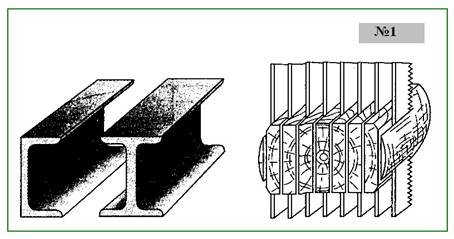
ІІІ. Закріплення набутих знань 

Задача. Площини α і β паралельні. Доведіть, що кожна пряма площини α паралельна площині β.

Задача.  Доведіть, що через будь-яку з двох мимобіжних прямих можна провести площину, паралельну другій прямій. Виконайте цю побудову.

Задача. Доведіть, що коли дві площини, які перетинаються по прямій а, перетинають площину α по паралельних прямих, то пряма а паралельна площині α.

Задача. Доведіть, що геометричне місце середин відрізків з кінцями на двох мимобіжних прямих є площина, паралельна цим прямим.

Розв’язання.

 

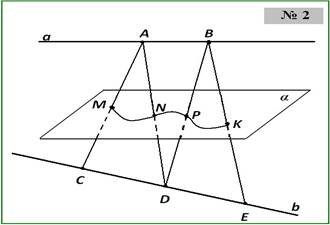
Нехай а і b – мимобіжні прямі. Проведемо відрізки АС, AD, BD, BE, кінці яких знаходяться на прямих а і b (кодопозитив №2). Точки M, N, P, K є серединами проведених відрізків відповідно. Сполучимо середини цих відрізків. Очевидно, що МN – середня лінія ∆ACD, NP – середня лінія ∆ABD, PK – середня лінія ∆BDE.

За властивістю середньої лінії трикутника MN || CD, NP || AB, PK || DE або MN || b, NP || a, PK || b. Оскільки прямі MN і NP мають спільну точку N, то вони перетинаються, і, отже, через них можна провести площину. Прямі NP і PK мають спільну точку P, і через них також можна провести площину. MN ||

PK згідно з ознакою паралельності прямих. З цього випливає, що через них можна провести площину. Таким чином, прямі MN, NP, PK лежать в одній площині α.

Аналогічно доводиться, що середини інших відрізків, які сполучають точки на прямих а і b, лежать в одній площині α.

Оскільки MN || b, то можна стверджувати, що b || α (за ознакою паралельності прямої і площини). Аналогічно а || α.

Таким чином, площина α паралельна водночас двом мимобіжним прямим а і b. Це означає, що геометричним місцем середин відрізків з кінцями на двох мимобіжних прямих є площина, паралельна цим двом прямим, що й треба було довести.

IV. Підсумок уроку

ü Як можуть розташовуватись дві площини у просторі?

ü Які площини називаються паралельними?

V. Завдання додому

§6;  завдання – знайти і розв’язати дві задачі, що стосуються сьогоднішнього навчального матеріалу.

 

Тема уроку.        Ознака паралельності площин.

Обладнання:      кодопозитиви, стереометричний набір.

Хід уроку

І. Аналіз самостійної роботи ІІ. Пояснення нового матеріалу

Вчитель. Які дві площини називаються паралельними?

Учні. Дві площини називаються паралельними, якщо вони не перетинаються.

Вчитель. На практиці для встановлення паралельності площин користуються наступною теоремою.

Теорема 6 (ознака паралельності площин). Якщо дві прямі, які перетинаються і лежать в одній площині, паралельні двом прямим другої площини, то такі площини паралельні.

Доведення.

Учні самостійно розбирають доведення теореми за допомогою кодопозитива №1.

ІІІ. Закріплення нових знань

Задача.  Доведіть, що площини α і β паралельні, якщо дві прямі а і b, які лежать у площині α і перетинаються, паралельні площині β.

Задача.  Дві сторони паралелограма паралельні площині α. Чи паралельні діагоналі паралелограма цій площині?

Задача.  Бічні сторони трапеції паралельні площині β. Чи паралельні основи цієї трапеції площині β ?

Задача.  Площини α і β паралельні, точка А – належить площині α. Доведіть, що кожна пряма, яка проходить через точку А і паралельна площині β, лежить у площині α.

Задача.  Пряма а паралельна площині α. Проведіть через дану пряму площину, паралельну цій площині.

Задача.  Як через точку поза площиною провести площину, паралельну даній площині? Виконайте побудову.

Задача (додаткова). Умова задачі на кодопозитиві №2.

                                                           Задача                                    Кодопозитив № 2

Доведіть, що коли чотири прямі проходять через точку А і перетинають площину α у вершинах паралелограма, то вони перетинають будь-яку площину, яка паралельна α і не проходить через точку

А, також у вершинах паралелограма.

 

IV. Підсумок уроку

Ø    Сформулюйте ознаку паралельності площин.

Ø    Дві сторони трапеції паралельні площині α. Як розташовані діагоналі цієї трапеції відносно площини α? Чому? V. Завдання додому §6; наступні задачі:

Задача.  Площина α перетинає тетраедр і проходить через середини його бічних ребер. Доведіть, що ця площина паралельна площині, що містить його основу.

Задача.  Точка О – спільна середина кожного з відрізків АА₁, ВВ₁, СС₁,

які не лежать в одній площині. Доведіть, що (АВС)  (А₁В₁С₁)/

 

             Тема уроку.          Існування площини, паралельної до даної площини.

             Обладнання:        Microsoft PowerPoint, стереометричний набір.

Хід уроку

І. Актуалізація опорних знань учнів

Проведення тесту на визначення істинності математичних тверджень. Інструкція. Вчитель читає твердження, а учні ставлять «+» якщо твердження правильне, і « – » якщо воно хибне. Правильність визначення істинності твердження оцінюється 1 балом.

Тест

1)         Якщо α || β, то будь-яка пряма площини α паралельна площині β. (+)

2)         Якщо α || β, то будь-яка пряма площини α паралельна кожній прямій площини β. (-)

3)         Якщо α || β, то будь-яка пряма площини α мимобіжна кожній прямій площини β. (-)

4)         Якщо α || β, то для будь-якої прямої а площини α існує така пряма b в площині β, що а || b. (+)

5)         Якщо α || β, то для будь-якої прямої а площини α існує така пряма b в площині β, що прямі а і b – мимобіжні. (+)

6)         Якщо α || β, то будь-яка пряма, яка перетинає площину α, перетинає і площину β. (+)

7)         Якщо α || β, то будь-яка пряма, паралельна площині α, паралельна і площині β. (-)

8)         Якщо дві прямі площини α паралельні відповідно двом прямим площини β, то α || β. (-)

9)         Якщо деяка пряма площини α паралельна площині β, то й α || β. (-)

10)    Якщо кожна пряма площини α паралельна площині β, то α || β. (+)

11)    Якщо дві прямі, одна з яких лежить у площині α, а друга – у площині β, не мають спільних точок, то α || β. (-)

12)    Якщо кожні дві прямі, одна з яких лежать в площині α, а друга – в площині β, не мають спільних точок, то α || β. (+)

ІІ. Сприйняття нового матеріалу

Вчитель. Як ви вважаєте, скільки площин, паралельних даній площині, можна провести через дану точку?

При обговоренні варто звернути увагу учнів на два можливих випадки: 1) дана точка належить даній площині; 2) дана точка лежить поза даною площиною.

Теорема (про існування площини, паралельної даній площині). Через точку поза даною площиною можна провести площину, паралельну даній, і до того ж тільки одну.

Доведення.

Працюючи зі слайдом 1, учні самостійно розбирають доведення існування площини, вказаної в умові теореми. Роблять відповідні записи в зошитах.

 

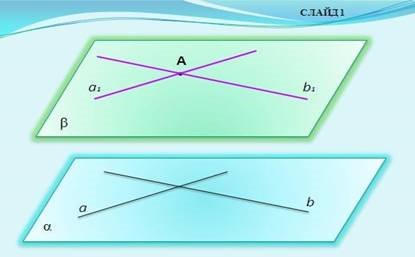
Запис може бути таким:

«Дано:   α,   А  α.

Довести:   β, що   β || α,    А  β.

Доведення.

Проводимо в площині  α  дві прямі  а і b, які перетинаються Через

точку А проведемо прямі  а₁  і  b₁ такі, що а₁ || а   та    b₁ ||  b. Через прямі  а₁  і  b₁ проведемо площину β, яка буде паралельна площині  α. »

Вчитель звертає увагу учнів на те, що безпосередньо з доведення існування площини  β не випливає, що  β  – єдина, бо прямі а і b вибрані довільно, тому може статись, що другій парі таких прямих буде відповідати інша площина, паралельна площині  α. Тому далі працюємо зі слайдом 2.

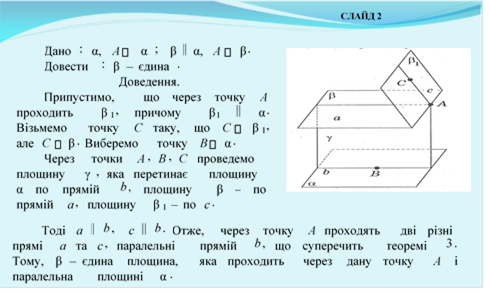
ІІІ. Закріплення набутих знань

Задача.  Доведіть, що якщо площина γ перетинає одну з двох паралельних площин α або β, то вона перетинає і другу площину.

Задача.   

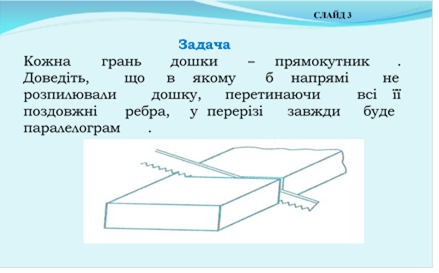
Задача.  Чи можуть перетинатись площини α і β, якщо кожна з них паралельна площині γ? Відповідь обґрунтуйте.

Задача.  Доведіть, що через будь-які мимобіжні прямі можна провести єдину пару паралельних площин.

Задача.  Паралелограми АВСD і АВС₁D₁ лежать в різних площинах.

Доведіть, що чотирикутник СDD₁С₁ також паралелограм.

IV. Підсумок уроку

Скільки площин, паралельних даній площині, можна провести через точку, яка:

а) належить даній площині;          б) не належить даній площині?

V. Завдання додому

§6 ;  виконати наступні завдання 

Завдання 1: побудувати площину, яка проходить через дану точку і паралельна даній площині.

Завдання 2: зробити з картону або цупкого паперу модель перетину двох паралельних площин третьою площиною.

 

Тема уроку.        Властивості паралельних площин.

Обладнання:      кодопозитиви, стереометричний набір.

Хід уроку

І. Актуалізація опорних знань

Математичний диктант

Дано зображення куба: варіант 1 – зліва, варіант 2 – справа.

 

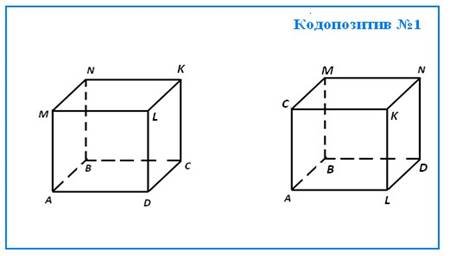
Користуючись зображенням, запишіть:

1)    площину, яка паралельна площині (АВС);

2)    площину, яка паралельна площині (CNL);

3)    площину, яка паралельна площині (MKD);

4)    паралельні площини, які містять мимобіжні прямі MK і AB;

5)    паралельні площини, які проходять через мимобіжні прямі AB і KD;

6)    площину, яка паралельна площині (MLK) і містить пряму АD.

Відповіді до тесту

	1	2	3	4	5	6
Варіант 1	MNK	BDM	ACN	ABC, KLM	ABM, CKD	ABC
Варіант 2	LNK	ADM	BCL	ABD, CKM	ABC, DKL	ABD

ІІ. Пояснення нового матеріалу

Вчитель. У кожного з вас є своя модель двох паралельних площин, які перетинаються третьою площиною. Покажіть лінії перетину цих площин. Що можна сказати про взаємне розташування цих прямих?

Учні. Лінії перетину паралельних площин третьою площиною паралельні між собою.

Теорема 7. Паралельні площини перетинаються січною площиною по паралельних прямих.

 

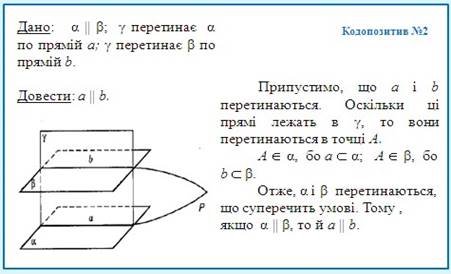
Теорема 8. Паралельні площини, перетинаючи паралельні прямі, відтинають від них рівні відрізки.

 

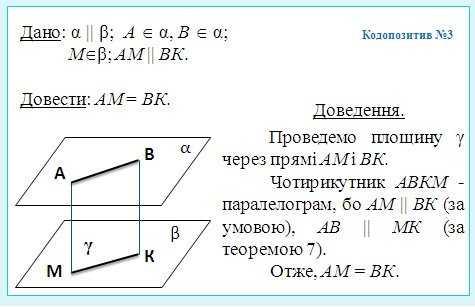
ІІІ. Закріплення набутих знань

Задача.  Доведіть, що коли перерізом паралелепіпеда є шестикутник, то його протилежні сторони паралельні.

Задача.  Рівні трикутники АВС і КРТ розміщені в площинах α і β так, що прямі АК, ВР і СТ паралельні. Чи вірно, що α || β?

Задача.

 

Задача.

 

Задача.  АВСDEFA – неплоска замкнена ламана з шести ланок.

Доведіть, що коли  AB || DE, BC || EF і  CD || FA, то AB=DE, BC=EF, CD=FA.

Задача.  Доведіть, що два кути з відповідно паралельними сторонами  або рівні, або їх сума дорівнює 180^о.

IV. Підсумок уроку

ü Сформулюйте теорему про лінії перетину двох паралельних площин січною площиною.

ü Дві паралельні площини α і β перетинаються площиною γ по прямих а і b. Вкажіть, чи правильне твердження:

-         прямі а і b можуть бути мимобіжними;

-         прямі а і b обов’язково паралельні;

-         пряма а паралельна площині β;

-         будь-яка пряма, яка лежить у площині γ, обов’язково перетинає площини α і β.

ü Сформулюйте теорему про властивість паралельних відрізків, які лежать між паралельними площинами.

V. Завдання додому

§6;  задачі № 96, № 99.

 

Тема уроку.  Кут між прямими. Перпендикулярність прямих у просторі Обладнання:  стереометричний набір, кодоплівки.

Хід уроку

І.  Актуалізація опорних знань

1.     Сформулюйте    означення   перпендикулярних        прямих       на площині.

2.     Згадайте аксіоми стереометрії.

3.     Сформулюйте ознаки паралельності в просторі.

ІІ. Пояснення нового матеріалу

Поряд з відношенням паралельності в геометрії важливе значення має відношення перпендикулярності. У планіметрії ми говорили про перпендикулярність прямих. Як вже згадувалось, на площині перпендикулярними називаються прямі, які перетинаються під прямим кутом.

У стереометрії розглядається три випадки перпендикулярності:

-                перпендикулярність прямих;

-                перпендикулярність прямої і площини; -    перпендикулярність площин.

Вчитель. Дві прямі, які перетинаються, утворюють чотири кути. Якщо всі ці кути рівні, то дані прямі перпендикулярні.

Означення. Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.

Завдання. Назвіть в оточенні моделі перпендикулярних прямих.

Вчитель. Якщо не всі ці кути рівні, то кутову міру меншого з них називають кутом між даними прямими. Вважається також, що кут між паралельними прямими дорівнює 0^о. Кут між прямими, що перетинаються, не перевищує 90^о. Усе це відомо з планіметрії і залишається правильним для прямих, які перетинаються в просторі. Щоб ввести поняття кута між мимобіжними прямими, доведемо таку теорему.

Далі формулюється теорема.

Теорема 10. Якщо дві прямі, які перетинаються, паралельні іншим прямим, які перетинаються, то кут між першими прямими дорівнює куту між другими прямими.

Доведення.

Прямі АВ і АС, які перетинаються, паралельні відповідно прямим КМ і КТ (мал. 1). Доведемо, що кут між прямими АВ і АС дорівнює куту між прямими КМ і КТ.

 

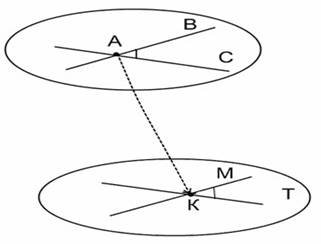
Мал. 1

Паралельне перенесення на вектор АК відображає пряму АВ на паралельну їй пряму, що проходить через точку К, тобто – на КМ. Те саме паралельне перенесення відображає пряму АС на паралельну їй пряму КТ. Тому менший із кутів, утворених при перетині прямих АВ і АС, дорівнює меншому з кутів, утворених при перетині прямих КМ і КТ, що й треба було довести.

Вчитель. Доведена теорема дає можливість ввести поняття кута між мимобіжними прямими.

Нехай а і b – довільні мимобіжні прямі (мал. 2). Через будь-яку точку О простору проведемо прямі а₁ і b₁, паралельні даними прямим а і b. 

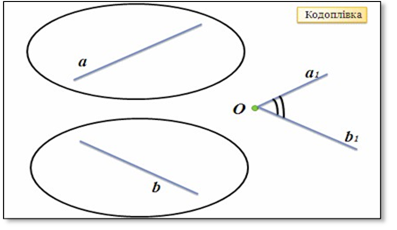
Мал. 2

Кут між прямими а₁ і b₁, які перетинаються, приймається за кут між даними мимобіжними прямими а і b. Цей кут не залежить від вибору точки О, адже якщо через будь-яку іншу точку простору провести прямі, паралельні даним мимобіжним прямим а і b, то за доведеною теоремою кут між ними буде такий самий.

Означення. Кутом між мимобіжними прямими називається кут між прямими, які перетинаються і паралельні даними прямим.

Отже, можна говорити про кут між будь-якими двома прямими простору. Кут між прямими а і b позначають (аb).

Означення. Дві прямі називаються перпендикулярними, якщо кут між ними прямий.

Вчитель.   Перпендикулярними     можуть       бути як      прямі,         що перетинаються, так і мимобіжні прямі. Назвіть у кубі АВСDА₁В₁С₁D₁ прямі, перпендикулярні до прямої АА₁ (мал. 3)

 

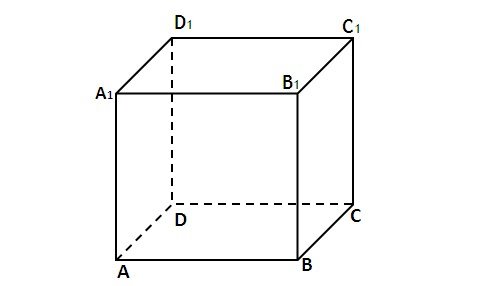
Мал. 3

Учні. У кубі АВСDА₁В₁С₁D₁ кожна з прямих АВ, ВС, СD, А₁В₁, В₁С₁, С₁D₁, D₁А₁ перпендикулярна до прямої АА₁.

Означення. Два відрізки називаються перпендикулярними, якщо вони належать перпендикулярним прямим.

Далі формулюється теорема.

Теорема 11. Якщо пряма перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до другої.

Доведення.

Учні доводять самостійно за готовим малюнком, який виводиться на екран з кодоплівки (мал. 4).

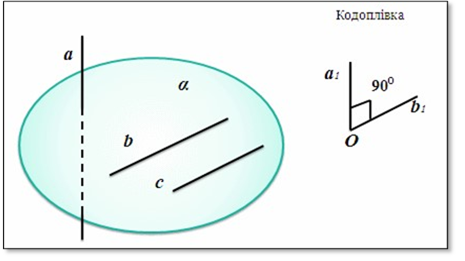
Мал. 4

Нехай а  b  і  b || с. Доведемо, що а  с.

Через довільну точку  О  простору проведемо прямі  а₁ і  b₁ такі, що   а₁ || а  і b₁ || b. Тоді маємо с || b₁.

(а₁b₁) – кут як між прямими  а і b, так і між прямими а і с, тобто 

aca₁b₁(ab) 90^o .

Отже, а  с, що й треба було довести.

ІІІ. Розв’язування задач

1.            Доведіть, що через будь-яку точку прямої у просторі можна провести перпендикулярну до неї пряму.

Доведення.

Нехай  а – дана пряма і А – точка на ній (мал. 5). 

 

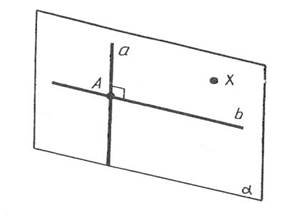
Мал. 5

Візьмемо поза прямою а довільну точку Х  і проведемо через цю точку і дану пряму  а площину  α. У площині  α  через точку А можна провести єдину пряму  b, перпендикулярну до прямої  а.

2.            Задача з кодоплівки (мал. 6).

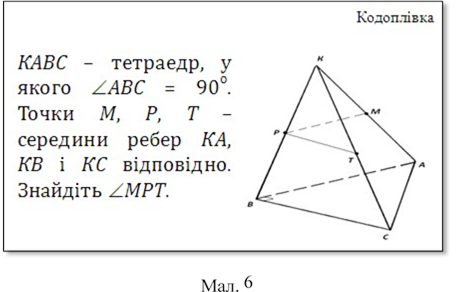
3.            Доведіть, що пряма, перпендикулярна до двох прямих, які перетинаються, перетинає площину, що проходить через ці прямі.

Розв’язання.

Робота з підручником (№ 131, с.45).

4.            Доведіть, що через будь-яку точку прямої у просторі можна провести дві різні перпендикулярні прямі.

Доведення.

ІV. Підсумки уроку

1.          Які прямі в просторі називаються перпендикулярними?

2.          Чи визначають площину дві перпендикулярні прямі? Чому?

3.          Сформулюйте теорему 10.

4.          Про що говорить теорема 11 ?

V. Домашнє завдання

§8,   розв’язати наступні задачі:

1.     АВСDА₁В₁С₁D₁ – прямокутний паралелепіпед. Знайдіть кут між прямими АD₁ і В₁С, якщо:   а) В₁СВ = 50⁰;  б) ВС = а, ВС₁ = 2а.

2.     Чи існує замкнена неплоска ламана з п’яти ланок, кожна з яких перпендикулярна до суміжної?

3.     Прямі АВ, АС і AD попарно перпендикулярні (мал. 8). Знайдіть відрізок СD, якщо АВ = b , ВС = а , АD = d.

 

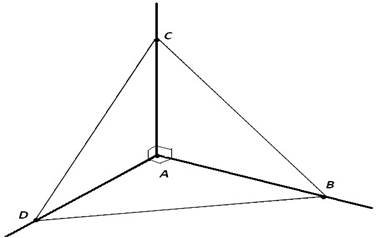
Мал. 8

Розв’язання.

Розглянемо трикутник АВС. За теоремою Піфагора:

АС BC² AB²  a² b² .

З трикутника АСD знайдемо:

Отже, СD =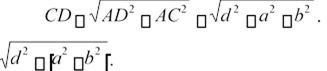

 

Тема уроку.        Перпендикулярність      прямої        і         площини.    Ознака перпендикулярності прямої і площини

Обладнання:      модель куба, кодопозитиви, стереометричний набір.

Хід уроку

І.  Актуалізація опорних знань учнів

ü   Які дві прямі у просторі називаються перпендикулярними?

ü   Сформулюйте теорему про перпендикулярні прямі у просторі. 

ü   Сформулюйте означення паралельних прямої і площини.

ІІ. Пояснення нового матеріалу

Вчитель. Якщо пряма не лежить у площині і не паралельна їй, то вона перетинає цю площину.

Нехай пряма АО перетинає площину α в точці О, а прямі ОВ, ОС, ОD, … лежать у площині α (мал. 1). Кути АОВ, АОС, АОD, … можуть бути різними.

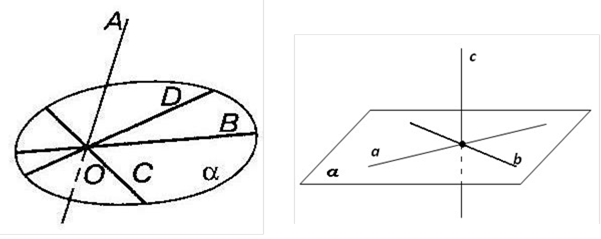
                                   Мал. 1                                                           Мал. 2

У випадку, коли всі ці кути прямі, говорять, що пряма АО

перпендикулярна до площини α. Пишуть: АО  α, або α  АО.

На мал. 2 пряма с перпендикулярна площині α, тобто с  α.

Уявлення про    пряму,        перпендикулярну          до      площини     дають вертикально поставлені стовпи – вони перпендикулярні до поверхні землі чи до будь-якої прямої цієї поверхні, яка проходить через основу стовпа. 

Означення. Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину і перпендикулярна до кожної прямої, що лежить у площині і проходить через точку перетину.

Завдання 1. Укажіть в оточуючому середовищі моделі прямих і площин, які перпендикулярні.

Завдання 2. Що означає твердження: пряма не перпендикулярна до площини?

Завдання 3. Чи правильно, що коли пряма не перпендикулярна до площини, то вона не перпендикулярна ні до жодної прямої, яка лежить в цій площині.

Вчитель. Як перевірити, чи перпендикулярна дана пряма до даної площини? Це питання має практичне значення, наприклад, при установці щогл, колон тощо, які потрібно поставити прямо, тобто перпендикулярно до поверхні землі.

Насправді немає необхідності перевіряти перпендикулярність прямої до всіх прямих, що лежать у даній площині  й проходять через точку перетину даної прямої і площини. 

Відповідь на це питання дає наступна теорема, що виражає ознаку перпендикулярності прямої і площини.

Мал. 2

Далі учні працюють з плівкою (мал. 2), конспектуючи кроки доведення наступної теореми.

Вчитель. Доведену теорему можна узагальнити. На основі останньої теореми з попереднього параграфа пряму АО можна замінити будь-якою прямою КР, паралельною їй, а пряму ОХ – будь-якою прямою ЕF, що лежить у площині α і паралельна ОХ (мал. 3). 

 

Мал. 3

З цієї теореми випливають такі наслідки:

ü пряма, перпендикулярна до двох прямих, що перетинаються, перпендикулярна до площини, що проходить через ці дві прямі;

ü пряма, перпендикулярна до площини, перпендикулярна до будьякої прямої, що лежить у цій площині;

ü якщо пряма перпендикулярна до двох сторін трикутника, то вона перпендикулярна і до третьої його сторони. ІІІ. Закріплення набутих знань

 Дано зображення куба АВСDА₁В₁С₁D₁. Довести, що:

             а) АВ₁С₁D - прямокутник;                          б) В₁D₁  (А₁С₁С).

 Задача з кодоплівки (мал. 4).

 

Мал. 4

 АВСDА₁В₁С₁D₁ – куб. доведіть, що пряма АС перпендикулярна до площини (ВВ₁D₁).

 Центр описаного навколо трикутника кола проведено пряму, перпендикулярну до площини трикутника. Доведіть, що кожна точка цієї прямої рівновіддалена від вершин трикутника (мал. 5).

                                                                

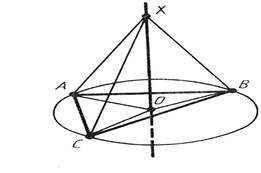
Мал. 5

ІV. Підсумки уроку

Ø   Яка пряма називається перпендикулярною до площини?

Ø   Сформулюйте ознаку перпендикулярності прямої і площини. V. Домашнє завдання

§9;   задачі № 144, № 147, № 148.

 

Тема уроку.        Властивості прямої і площини, перпендикулярних між собою

Обладнання:  стереометричний набір, кодопозитиви, схема «Прямі та площини, перпендикулярні між собою». Хід уроку

І.  Актуалізація опорних знань учнів

Математичний диктант

Користуючись зображенням куба, запишіть (варіант 1 – мал. 1, варіант 2 – мал. 2 з кодопозитива № 1) :

-    площину, яка проходить через точку М прямої АМ і перпендикулярна до неї (2 бали);

-    пряму, яка перпендикулярна до площини (АВС) і проходить через точку D (2 бали);  пряму, яка перпендикулярна до площини (АВС) і проходить через точку N (2 бали);

-    площину, яка перпендикулярна до прямої ВD (2 бали);

-    прямі, перпендикулярні до площини (АМС)  (2 бали);

-    площини, які перпендикулярні до прямої DС (2 бали).

 

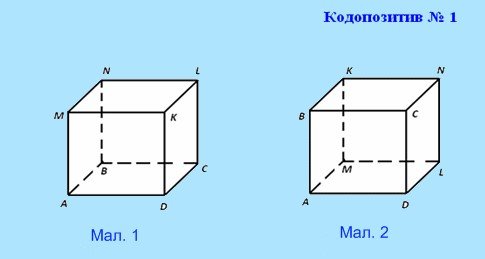
ІІ. Пояснення нового матеріалу

Властивість 1 (теорема 13). Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої.

Доведення.

Нехай а₁ і а₂— дві паралельні прямі і  α — площина, перпендикулярна до прямої  а₁ (мал. 3). Доведемо, що ця площина перпендикулярна й до прямої а₂.

 

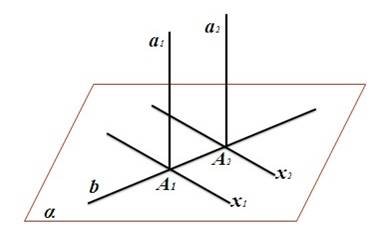
Мал. 3

Проведемо через точку А₂ перетину прямої а₂ з площиною  α довільну пряму х₂ у площині  α. Проведемо у площині  α  через точку А₁ перетину прямої  а₁ з  α  пряму х₁ , паралельну прямій  х₂. 

Оскільки пряма а₁ перпендикулярна до площини  α, то прямі а₁ і х₁ перпендикулярні. А за теоремою 3.1 паралельні до них прямі а₂ і х₂ , що перетинаються, теж перпендикулярні.

Таким чином, пряма а₂ перпендикулярна до будь-якої прямої х₂ у площині  α. А це означає, що пряма а₂ перпендикулярна до площини 

α. Теорему доведено.

Властивість 2 (теорема 14). Дві прямі, перпендикулярні до однієї площини, паралельні.

Доведення.

Нехай а  і  b – дві прямі, перпендикулярні до площини α (мал. 4).

Припустимо, що прямі а і b не паралельні. 

 

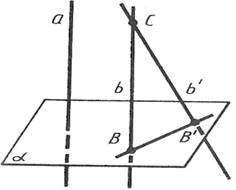
Мал. 4

Виберемо на прямій  b точку С, що не лежить на площині  α. Проведемо через точку С пряму  b', паралельну прямій а. Пряма  b' перпендикулярна до площини  α. 

Нехай В і В' — точки перетину прямих  b  і  b' з площиною  α. Тоді пряма ВВ' перпендикулярна до прямих  b і b', які перетинаються.

А це неможливо. Ми прийшли до суперечності. Теорему доведено.

Вчитель. Існують ще дві властивості прямих і площин, перпендикулярних між собою.

Властивість 3. Якщо пряма перпендикулярна до однієї з двох паралельних площин, то вона перпендикулярна і до другої.

Властивість 4. Якщо дві площини перпендикулярні до однієї і тієї самої прямої, то вони паралельні.

ІІІ. Розв’язування задач

1.            Доведіть, що через будь-яку точку А можна на провести пряму, перпендикулярну до даної площини α. 

Доведення.

Проведемо у площині α дві прямі b і с, що перетинаються (мал. 5). Через точку їх перетину проведемо площини  β і  γ, перпендикулярні до прямих  b  і с відповідно. Перетином їх буде пряма а.

 

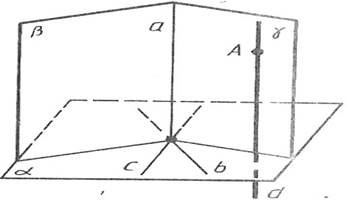
                                                                                                    Мал. 5

Пряма а перпендикулярна до прямих  b  і с, отже, і до площини 

α. Проведемо тепер через точку А пряму d, паралельну а. За теоремою

3.3 вона перпендикулярна до площини  α .

 

2.            Через вершину квадрата ABCD проведено пряму ВМ, перпендикулярну до його площини. Доведіть, що: 

1) пряма AD перпендикулярна до площини прямих АВ і ВМ;  2) пряма CD перпендикулярна до площини прямих ВС і ВМ.

 

 

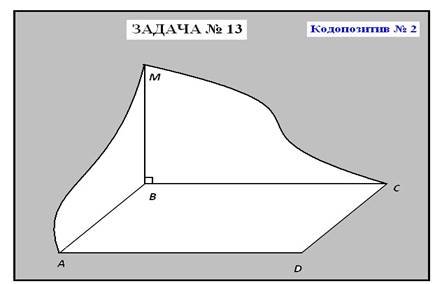
3.            Телефонний провід завдовжки 15 м протягнуто від телефонного стовпа, де він прикріплений на висоті 8 м від поверхні землі, до будинку, де його прикріпили на висоті 20 м. Знайдіть відстань між будинком і стовпом, вважаючи, що провід не провисає.

 

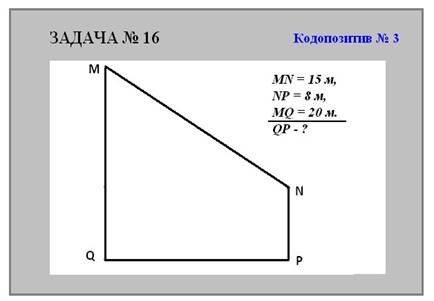
V. Підведення підсумків уроку

При підведенні підсумку уроку доцільно скористатись наступною схемою.

 

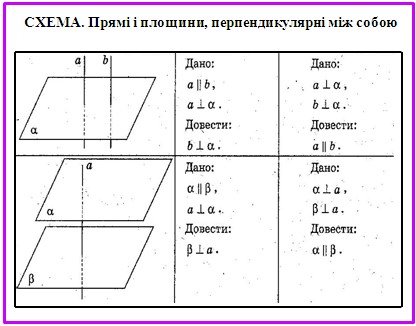
ü   Як розташовані прямі, які перпендикулярні до площини?

ü   Як розташовані в просторі площини, перпендикулярні до даної прямої?

ü   Як розташовані пряма і площина, якщо паралельна пряма до даної прямої буде перпендикулярною до площини?

IV. Домашнє завдання

§9;    довести властивості 3 і 4.

 

Тема уроку.        Теорема про три перпендикуляри

Обладнання:      стереометричний набір, кодопозитиви.

Хід уроку І. Перевірка домашнього завдання ІІ. Пояснення нового матеріалу

Сформулюємо і доведемо теорему про три перпендикуляри.

Теорема 15. Пряма, проведена на площині перпендикулярно до проекції похилої, перпендикулярна до цієї похилої. І навпаки, якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції цієї похилої.

Доведення.

Робота з кодоплівкою.

Вчитель. З наведених міркувань випливає, що коли пряма КР не перпендикулярна до ВС, то вона й не перпендикулярна до АВ. Тому теорему про три перпендикуляри можна сформулювати одним реченням.

Пряма, яка лежить у площині, перпендикулярна до похилої тоді і тільки тоді, коли вона буде перпендикулярною до проекції цієї похилої.

Теорему про три перпендикуляри названо так, маючи на увазі

перпендикуляри АС  α,  ВС  КР,  АВ  КР.

Теорема 16. Якщо з однієї точки, взятої поза площиною, проведені до цієї площини перпендикуляр і похила, то:

1)    проекції рівних похилих рівні;

2)    з двох похилих більшою є та, у якої більша проекція; 3) перпендикуляр коротший за будь-яку похилу.

Вчитель.   Ця     теорема      випливає     з        властивостей        прямокутних трикутників. Спробуйте довести її самостійно.

Вчитель. Назвіть приклади моделей перпендикуляра чи похилої до площини.

Учні. Стовп, телевізійна вежа, ніжка стільця є прикладами перпендикуляра. Якщо дротом з’єднати верхівку стовпа з кінцем тіні від стовпа на поверхні землі, то дріт буде моделлю похилої, а тінь стовпа – моделлю проекції цієї похилої.

ІІІ. Закріплення набутих знань

1.     Дано: DВ  (АВС), ВАС = 30⁰, АВС = 60⁰ (мал. 1).

Довести:  СD  АС.

2.     Дано: DА  (АВС), ВАС = 40⁰, АСВ =50⁰ (мал. 2).

Довести:  СВ  DВ.

 

                              Мал. 1                                          Мал. 2

3.     До площини квадрата АВСD проведено перпендикуляр МВ. Точка М сполучена з вершинами квадрата. Визначте вид трикутника МАD.

4.     Визначте вид трикутника МАС, якщо М – точка, з якої проведений

перпендикуляр до площини АВС з прямим кутом С.

5.     До площини ромба АВСD проведено перпендикуляр ТВ. Доведіть, що

ТО  АС, якщо О – точка перетину діагоналей ромба.

ІV. Підсумки уроку

Ø   Сформулюйте теорему про три перпендикуляри.

Ø   Які теореми і означення використовуються для її доведення?

Ø   Вкажіть взаємне розташування прямих а і b (кодоплівка).

 

V. Домашнє завдання

§10;   задачі № 157,  № 159,  №164.

 

Тема уроку.                      Відстань від точки до прямої. Властивість точки,

рівновіддаленої від сторін многокутника.

Обладнання:  кодопозитиви, стереометричний набір, стінна таблиця з формулами для знаходження радіусів вписаного кола . Хід уроку

І. Актуалізація опорних знань учнів

Математичний диктант

АВСD – прямокутник (кодопозитив 1), КА  (АВС).

Варіант 1 – КА 3 см, АВ1см, ВС 3см.

Варіант 2 – КА 2 м, АВ1 м, ВС 2 м.

Користуючись зображенням, знайдіть:

1)            довжину відрізка КВ;

2)            довжину діагоналі АС;

3)            довжину похилої КD;

4)            величину кута КВС;

5)            величину кута КDС;

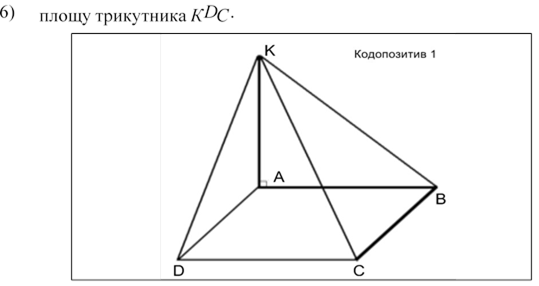
Запитання до класу

1.             Що називається перпендикуляром?  похилою?

2.             Сформулюйте теорему про три перпендикуляри.

ІІ. Усвідомлення нового матеріалу

Нехай задані в просторі пряма а і точка А, що не лежить на даній прямій.

Означення. Відстанню від точки А до прямої а називається довжина перпендикуляра, опущеного з цієї точки на дану пряму.

 

Завдання. З точки М опустіть перпендикуляр на пряму АВ (мал. 1).

 

Мал. 1

Вчитель. Розглянемо задачу: через центр вписаного в трикутник кола проведено пряму, перпендикулярну до площини трикутника. Доведіть, що кожна точка цієї прямої рівновіддалена від сторін трикутника.

Після розв’язування задачі слід зробити висновок, який учні повинні записати: якщо через центр кола, вписаного в многокутник, проведено перпендикуляр до площини цього многокутника, то кожна точка перпендикуляра рівновіддалена від сторін многокутника.

Такою задачею доцільно підводити учнів до вивчення властивості точки, рівновіддаленої від сторін многокутника. 

Теорема. Якщо точка рівновіддалена від сторін многокутника і основа перпендикуляра, опущеного з цієї точки до площини многокутника, лежить всередині многокутника, то основа перпендикуляра є центром кола, вписаного в даний многокутник.

Доведення.

При доведенні користуємось кодопозитивом 2.

 

Далі доцільно пригадати формули для знаходження радіуса кола, вписаного в многокутник, за допомогою наступної стінної таблиці.

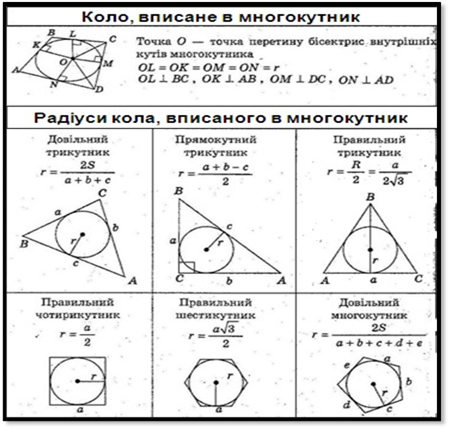
ІІІ. Задачі на закріплення знань

1.          Через точку О перетину діагоналей квадрата ABCD проведено до його площини перпендикуляр МО довжиною 15 см. Знайдіть відстань від точки М до сторін квадрата, якщо його сторона дорівнює 16 см. 

2.          Відрізок АК, що дорівнює 12 см, перпендикулярний до площини трикутника АВС, в якому АВ = АС = 20 см, ВС = 24 см. Знайдіть відстань від точки К до прямої ВС.

3.          Катет АС прямокутного трикутника дорівнює а, кут В дорівнює φ. Через вершину прямого кута проведено до площини цього трикутника перпендикуляр МС довжиною а. Знайдіть відстань від кінців перпендикуляра до гіпотенузи.

ІV. Підведення підсумків уроку

ü  Що називається відстанню від точки до прямої?

ü  Знайдіть відстань від точки  А  до прямої  а, якщо ребро куба дорівнює 2 см (кодопозитив 3).

 

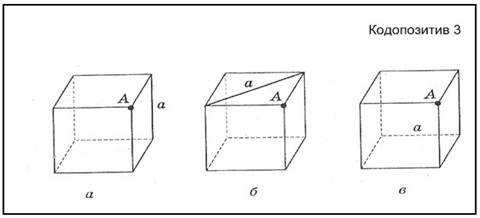
V. Домашнє завдання

Повторити  §10 ;  наступні задачі.

1.     З вершини прямокутника проведено перпендикуляр до його площини. Відстані від кінця цього перпендикуляра до решти вершин прямокутника дорівнюють а, b, с (а<с, b<с). Знайдіть довжину перпендикуляра і сторони прямокутника.

2.     З вершини рівностороннього трикутника ABC проведено перпендикуляр AD до площини трикутника. Знайдіть відстань від точки D до сторони ВС, якщо AD = 13см, ВС = 6см.

3.     №164.

 

Тема уроку.        Перпендикулярні площини. 

Обладнання:      стереометричний набір, моделі куба і прямокутного паралелепіпеда.

Хід уроку І. Актуалізація опорних знань учнів Фронтальне опитування:

ü   Сформулюйте аксіоми стереометрії.

ü   Які прямі в просторі називаються перпендикулярними?

ü   Сформулюйте ознаку перпендикулярності прямої і площини.

ІІ. Сприйняття нового матеріалу

Спочатку вводиться поняття кута між площинами.

Вчитель. Нехай α і  - площини, які перетинаються по прямій с (мал. 1). Проведемо в цих площинах через точку М прямі а і b такі, що ас, bс.

Позначимо (аb) = . Якщо в площинах α і  провести які-небудь інші прямі,

перпендикулярні до с, то кут між ними

також дорівнюватиме . Чому?

Учні. Тому, що ці прямі будуть паралельні прямим а і b відповідно.

Означення. Кутом між площинами, які перетинаються, називається гострий кут між прямими, проведеними в цих

                                        Мал. 1                             площинах перпендикулярно до лінії їх

перетину.

Вчитель. Чому дорівнює кут між паралельними площинами?

Учні. Якщо дві площини паралельні, то кут між ними дорівнює 0^o .

                   Означення.     Дві     площини,     що     перетинаються,     називаються

перпендикулярними, якщо кут між ними дорівнює 90^o.

На мал. 1  α  β, бо (ab)90^o .

ІІІ. Закріплення набутих знань

1.      Наведіть приклади моделей перпендикулярних площин із оточуючого середовища.

2.      Покажіть на моделі прямокутного паралелепіпеда перпендикулярні грані

3.      Скільки площин, які перетинають дану площину під кутом 50⁰, можна провести через дану точку?

4.      Пряма а перетинає площину α під кутом 45⁰. Чи можна через пряму а провести площину, яка перетинається з α під кутом 30⁰? 135⁰?

5.      З точок А і В, які лежать у двох перпендикулярних площинах, опущено перпендикуляри АС і ВD на пряму перетину площин.

Знайдіть довжину відрізка АВ, якщо: 

1) АD = 4 м, ВС = 7 м, СD = 1 м; 2) АС = а, ВD = b, СD = с.

ІV. Підведення підсумків уроку

•      Які площини називаються перпендикулярними?

•      Дано куб АВСDА₁В₁С₁D₁. Вкажіть площини, перпендикулярні площині (АDС).

V. Домашнє завдання

§12 ;  розв’язати  наступні  задачі.

 № 205 (с. 64).

 Дано:  α  ,  α   = с ;     α,     .     Довести:    с.

 З точок А і В, які лежать у двох перпендикулярних площинах, опущено перпендикуляри АС і ВD на пряму перетину площин.

Знайдіть довжину відрізка АВ, якщо:

1) АС = 3 м, ВD = 4 м, СD = 12 м;  2) АD = а, ВС = b, СD = с.

Тема уроку.        Ознака перпендикулярності площин.

Обладнання:      кодопозитиви, стереометричний набір.

Хід уроку

І. Актуалізація опорних знань

1.  Які прямі в просторі називаються перпендикулярними?

2.  Сформулюйте ознаку перпендикулярності прямої і площини.

3.  Дайте означення перпендикулярних площин.

ІІ. Пояснення нового матеріалу

Вчитель. Розглянемо задачу. Дано:  b  α,  b  . Довести, що α  .

Доведення.

Вчитель. Нехай О – точка перетину прямої b і площини α (мал. 1). Що можна сказати про взаємне розміщення площин α і ?

 

Мал. 1

Учні. Ці площини перетинаються по прямій с, яка проходить через точку О.

Вчитель. Проведемо в площині α через точку О пряму а  с. Як розташована пряма b по відношенню до прямих а і с ?

Учні. Оскільки b  α (за умовою), а прямі а і с належать площині α, то b  α  і b  с.

Вчитель. Крім того, а  с (за побудовою), тому (α) = … Учні. (α) = (аb) = 90⁰, тобто α  .

Вчитель. Таким чином, ми довели наступну теорему (ознаку перпендикулярності площин).

Теорема 18. Якщо одна з двох площин проходить через пряму, перпендикулярну до другої площини, то такі площини перпендикулярні.

Вчитель. Цю теорему використовують на практиці для спрощення процедури визначення перпендикулярності площин. Досить важливою є також і наступна теорема.

Теорема 19.  Пряма, проведена в одній з двох перпендикулярних площин перпендикулярно до прямої їх перетину, перпендикулярна до другої площини.

ІІІ. Закріплення набутих знань

1.     Як на практиці встановити, чи перпендикулярна площина стіни до площини підлоги?

2.     Дано пряму а і площину α. Проведіть через пряму а площину, перпендикулярну до площини α.

3.     Дано пряму а і площину α. Доведіть, що всі прямі, які перпендикулярні до площини α і перетинають пряму а, лежать в одній площині, перпендикулярній до площини α.  

Розв’язання.

Проведемо довільні прямі т  α  і п  α, що перетинають пряму а в точках М і N відповідно (мал. 2).  

За властивістю прямих, перпендикулярних до однієї площини, прямі т і п паралельні. Це означає, що через ці прямі можна провести площину β,

причому β  α.

 

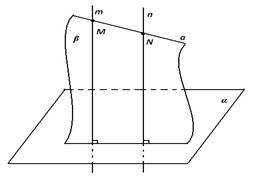
Мал. 2

Оскільки точки М і N лежать у площині β, то пряма а також лежить у цій площині. Таким чином, усі прямі, що перетинають пряму а і перпендикулярні до площини α, лежать у площині β.

4.     № 203.

5.     № 205 (с. 64) – робота з підручником. ІV. Підведення підсумків уроку

•      Які площини називаються перпендикулярними?

•      Дано куб АВСDА₁В₁С₁D₁. Вкажіть площини, перпендикулярні площині (АD₁С).

V. Домашнє завдання

§12 ;  задачі  № 202,  № 208,  № 209.

 

Основний курс математики має мало чим відрізнятися за номенклатурою навчальних питань від відповідного курсу в загальноосвітній школі. Відмінності в іншому: у глибині вивчення матеріалу, у формуванні критичного стилю мислення. Поглиблене вивчення математики зводиться до розширеного вивчення математики, яке є головною характеристикою сучасної програми для класів фізико-математичного профілю. 

Ефективність засвоєння знань учнями за умов широкого впровадження засобів нових інформаційних технологій навчання значною мірою залежить від педагогічних програмних засобів (ППЗ), що дають змогу поєднати високі моделюючі та обчислювальні можливості при дослідженні різноманітних математичних об’єктів з унаочненням результатів  на всіх етапах навчального  процесу. А різноманітні наочні посібники сприяють зростанню інтересу до математики, розвивають просторову уяву і допомагають краще засвоїти навчальний матеріал.

 

 

          

§3. Методика використання наочності при вивченні взаємного

розміщення прямих і площин в курсі стереометрії у вищих навчальних

закладах І-ІІ рівнів акредитації

Слід зазначити, що за більш ніж 20-літню практику використання комп’ютерної техніки, в процесі навчання математики з’явилася велика кількість комп’ютерних навчальних програм, проте не вироблені загальні методичні рекомендації викладачам про доцільність застосування тієї чи іншої комп’ютерної програми [36].

Доцільно було б мати для різних ВНЗ І-ІІ рівнів акредитації спеціальні навчальні посібники з математики, які б відображали в своєму змісті специфіку напряму підготовки фахівців даного навчального закладу. Проте поки що студенти, які навчаються у ВНЗ І-ІІ рівнів акредитації, вивчають математику за тими самими навчальними підручниками і посібниками, що й учні старших класів загальноосвітніх шкіл.

Особливістю даних навчальних закладів є те, що молодь, яка тут навчається, вже обрала спеціальність, тобто визначилась для себе з майбутнім фахом. Тому під час добору навчального матеріалу та вправ слід враховувати цю властивість [36].

Програми з математики для вищих навчальних закладів І-ІІ рівнів акредитації [87] майже не відрізняються від програм з математики для 10-12 класів загальноосвітніх навчальних закладів. Однак варто відмітити те, що кількість годин, які виділяються на вивчення тих чи інших тем курсу стереометрії студентами ВНЗ І-ІІ рівнів акредитації, мають тенденцію до зменшення, хоча вимоги до знань, вмінь і навичок залишаються незмінними.

І. Паралельність прямих і площин

Взаємне розміщення двох прямих у просторі

Ознака паралельності прямих

Взаємне розміщення прямої і площини у просторі. Паралельність прямої і площини. Ознака паралельності прямої і площини

Взаємне розміщення двох площин у просторі. Паралельність площин. Ознака паралельності площин

Властивості паралельних площин

ІІ. Перпендикулярність прямих і площин

Перпендикулярність прямих у просторі

Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини

Перпендикулярні площини. Ознака перпендикулярності площин

Відстань між мимобіжними прямими

Розглянемо методику використання наочних посібників при вивченні взаємного розміщення прямих і площин в курсі стереометрії.

 

Тема уроку.        Взаємне розміщення двох прямих у просторі

Обладнання:  каркасна модель куба, схема «Взаємне розміщення двох прямих у просторі»

Хід уроку І. Організаційна частина ІІ. Пояснення нового матеріалу

Вчитель. Із курсу планіметрії відомо, що дві прямі, які лежать у площині можуть перетинатися або не мати спільних точок. Сформулюйте означення паралельних прямих на площині.

Учні. Якщо дві прямі лежать в одній площині і не мають спільних точок, то вони називаються паралельними.

Вчитель. У просторі дві різні прямі або перетинаються, або не перетинаються. Перший випадок дає зрозуміти, що прямі лежать в одній площині. Проте другий випадок допускає дві можливості: прямі лежать в одній площині або ж вони належать різним площинам. 

Означення. Прямі, які лежать в одній площині і не перетинаються, називаються паралельними. А дві прямі, які не лежать в одній площині, називаються мимобіжними.

(Випадки взаємного розташування двох прямих у просторі доцільно демонструвати за допомогою каркасної моделі куба, ребра якого вважаючи прямими у просторі.)

Вчитель. Отже, дві прямі  а  і  b у просторі можуть: перетинатися, бути паралельними, бути мимобіжними (схема «Взаємне розміщення двох прямих у просторі»).

 

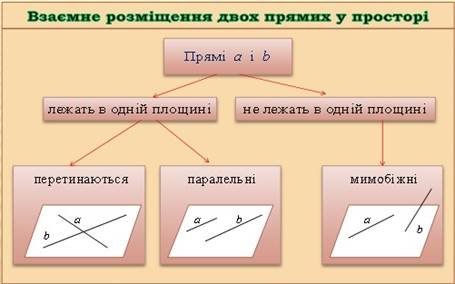
Вчитель. Пригадаємо аксіому ІХ з курсу планіметрії, яка вважається основною властивістю паралельних прямих.

Учні. Через точку, що не лежить на даній прямій, можна провести на площині пряму, паралельну даній, і до того ж тільки одну.

Вчитель. З цієї аксіоми паралельності випливає, що на площині через дану точку можна провести не більше однієї прямої, яка паралельна даній прямій. Давайте з’ясуємо, скільки таких прямих можна провести у просторі.

Нехай дано пряму а і точку А, що не лежить на ній (мал. 1).

 

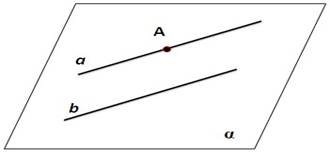
                                                       Мал. 1

Через них можна провести площину α (за теоремою 1.1). У цій площині можна провести пряму b, яка буде паралельною до даної прямої а.

Отже, у просторі через дану точку А можна провести пряму, паралельну прямій  а.

Таким чином, справедлива теорема (формулюють учні):

Теорема. Через точку, яка не лежить на даній прямій, можна провести пряму паралельну даній, і тільки одну.

Доведення.

Самостійна робота з підручником (с. 11). 

Запитання до класу

1.            Як треба розуміти, що дві прямі у просторі не паралельні?

2.            Що можна сказати про прямі у просторі, якщо відомо, що вони не мимобіжні?

3.            Як формулюється теорема, з доведенням якої ви ознайомились?

ІІІ. Закріплення набутих знань

№ 1. Доведіть, що коли прямі АВ і CD мимобіжні, то й мимобіжними будуть прямі АС і ВD.

№ 3. Доведіть, що всі прямі, які перетинають дві дані паралельні прямі, лежать в одній площині.

Доведення учні розбирають за підручником. (с. 10)

№ 5(4). Через кінці відрізка АВ і його середину М проведено паралельні прямі, що перетинають деяку площину в точках А₁, В₁ і М₁.

Знайдіть довжину відрізка  ММ₁ , якщо відрізок АВ не перетинає цю площину і відомо, що АА₁ = а,  ВВ₁ = b. 

№ 7 (1). Через кінець А відрізка АВ проведено площину. Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетинають площину в точках  В₁ і С₁. Знайдіть довжину відрізка  ВВ₁ , якщо СС₁=15 см, АС:ВС = 2:3.

№9. Прямі а і b не лежать в одній площині. Чи можна провести пряму с, паралельну прямим а і b?

IV. Домашнє завдання

§2, п. 7;   задачі № 5 (2), 7 (4) (с. 18-19).

V. Підведення підсумків уроку

1.  Як можуть розташовуватись дві прямі у просторі?

2.  Які прямі називаються паралельними?

 

Тема уроку.        Ознака паралельності прямих.

Обладнання:      моделі прямокутного паралелепіпеда і куба, кодопозитив.

Хід уроку

І. Актуалізація опорних знань учнів

1.                       Скільки прямих, паралельних даній прямій, можна провести у просторі через точку:

а) яка не лежить на даній прямій?

б) яка належить даній прямій?

2.                       Сформулюйте ознаки паралельності прямих на площині.

ІІ. Пояснення нового матеріалу

Вчитель. Які ознаки паралельності прямих вам відомі з курсу планіметрії, який вивчався в школі?

Учні. Є три ознаки паралельності прямих на площині: 

-           Якщо внутрішні різносторонні кути рівні, то прямі паралельні; 

-           Якщо сума внутрішніх односторонніх кутів дорівнює 180^о, то прямі паралельні;

-           Дві прямі, які паралельні третій, паралельні одна одній.

Вчитель. Перші дві ознаки паралельності не мають аналогів для прямих у просторі. Остання ж ознака справедлива і в стереометрії.

Сформулюємо її.

Теорема. Дві прямі, паралельні третій, паралельні між собою.

Доведення.

(Відповідно до тексту підручника.) ІІІ. Закріплення теоретичного матеріалу 1. Дано зображення куба. Доведіть, що AA₁ || СС₁ .

Доведення.

Вчитель. Зобразимо даний куб і позначимо його вершини (мал. 1).

Розглянемо квадрат  АА₁ВВ₁.

 

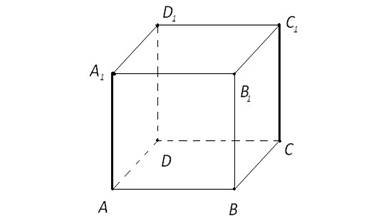
Мал. 1

Учні. Його сторони АА₁ і ВВ₁ паралельні. Аналогічно, у квадрата ВВ₁СС₁ паралельними будуть сторони ВВ₁ і СС₁.

З того, що АА₁ || ВВ₁ та  ВВ₁ || СС₁ випливає, що АА₁ || СС₁ .

2.            Прямі а і b паралельні, але прямі b та с не паралельні. Доведіть, що прямі а і с не паралельні.

3.            №11. Доведіть, що середини сторін просторового чотирикутника є вершинами паралелограма (вершини просторового чотирикутника не лежать в одній площині).

Доведення.

 

Мал. 2

Дана задача розв’язана в підручнику, проте саме розв’язання і зображення просторового чотирикутника знаходяться на різних сторонах аркуша книги, що приводить до певних незручностей. Тому доцільно запропонувати учням розібратись в ході розв’язання за допомогою наступного кодопозитива (мал. 2).

IV. Домашнє завдання

§2, п. 8;    задача № 9 (с. 19)

№9. Прямі а і b не лежать в одній площині. Чи можна провести пряму с , паралельну обом прямим?

V. Підведення підсумків уроку

1.  Сформулюйте ознаки паралельності прямих на площині.

2.  Сформулюйте ознаку паралельності у просторі.

 

 

 

Тема уроку.  Взаємне розміщення прямої і площини у просторі. Ознака паралельності прямої і площини.

Обладнання:                 моделі куба і тетраедра, схема «Взаємне розміщення

прямої і площини», кодопозитиви.

Хід уроку

І.  Актуалізація опорних знань учнів

1.     Згадайте і сформулюйте теорему про належність площині прямої, дві точки якої належать площині.

2.     Як можуть розміщуватись пряма і площина в просторі?

При обговоренні цього питання доцільно скористатись схемою «Взаємне розміщення прямої і площини» (мал. 1).

 

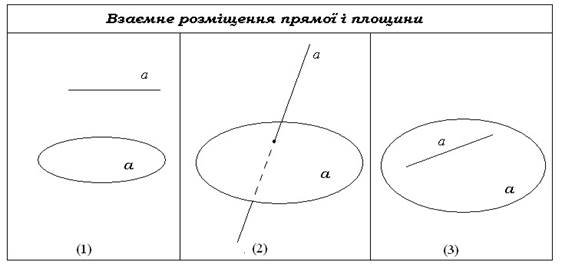
Мал. 1

ІІ. Пояснення нового матеріалу

Вчитель. За частиною (1) схеми можемо сказати, якщо пряма і площина не мають спільних точок, то вони паралельні.

Означення. Пряма і площина називаються паралельними, якщо вони не перетинаються.

Паралельність прямої а і площини α позначається так:  а || α. 

Вчитель. Назвіть в оточуючому середовищі моделі прямих і площин, які паралельні.

Учні. Наочним представленням прямої, яка паралельна площині, є лінії перетину стіни і стелі – ці лінії паралельні площині підлоги. 

Вчитель. Відрізок називається паралельним площині, якщо він є частиною прямої, паралельної площині.

Доведемо ознаку паралельності прямої і площини.

Теорема. Якщо пряма, яка не належить площині, паралельна якійнебудь прямій у цій площині, то вона паралельна і самій площині.  (Доведення записується на дошці і в зошиті.) Дано:  а || b,   bα.

Довести:  а || α .

Доведення.

Припустимо, що пряма а перетинає площину α , тобто пряма і площина мають спільну точку А. 

Якщо Аb, то а і b мають спільну точку А, що суперечить умові. Якщо

ж Аb, то прямі а і b мимобіжні, що знову суперечить умові.

Отже, припущення хибне, а тому а || α.

ІІІ. Розв’язування задач Задача 1.

 

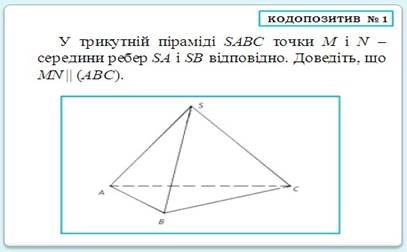
Задача 2.

№13 (1) (с. 19). Дано трикутник АВС. Площина, паралельна прямій АВ, перетинає сторону АС цього трикутника в точці А₁, а сторону ВС – в точці В₁.Знайдіть довжину відрізка А₁В₁, якщо АВ=15 см, АА₁ : АС = 2:3.

IV. Домашнє завдання

§2, п. 9;  задача № 14, 15 (с. 19)

№14. Через дану точку проведіть пряму, паралельну кожній з двох даних площин, які перетинаються.

№ 15. Доведіть, що коли площина перетинає одну з двох паралельних прямих, то вона перетинає й другу пряму.

 

Тема уроку.        Взаємне     розміщення     двох     площин          у     просторі.

Паралельність площин. Ознака паралельності площин Обладнання: моделі         куба   і         прямокутного      паралелепіпеда,   схема «Взаємне розміщення двох площин», кодопозитиви. Хід уроку

І.  Актуалізація опорних знань учнів ü Що означає : пряма і площина паралельні?

ü Сформулюйте аксіоми стереометрії. ü Що є перетином двох площин?

ІІ. Пояснення нового матеріалу

Вчитель. Ми знаємо, якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку. Чому?

Учні. За аксіомою С₂. 

Вчитель. Звідси випливає, що дві площини або перетинаються по прямій, або не перетинаються, тобто не мають спільних точок (демонструємо схему ).

 

Означення. Дві площини називаються паралельними, якщо вони не перетинаються.

Якщо площини α і β паралельні, то це позначається так:  α || β.

Завдання.

1.          Назвіть моделі паралельних прямих, які зустрічаються у вашій професії.

2.          На моделях куба і прямокутного паралелепіпеда покажіть паралельні площини і площини, що перетинаються.

3.          Користуючись зображенням прямокутного паралелепіпеда (мал. 1), вкажіть:

а) грані, які перетинають грань ABCD;

б) площини, які паралельні площині (ABC).

 

                                                   Мал. 1

Ознака паралельності площин формулюється і доводиться згідно з підручником.

Теорем. Якщо дві прямі, які перетинаються, однієї площини відповідно паралельні двом прямим другої площини, то ці площини паралельні.

Дано: а₁  α ;     а₂  α ;     а₁  а₂ = А;    b₁  β;     b₂  β;    а₁ || b₁;     а₂ || b₂  (мал. 2).

Довести:  α || β.

Доведення.

 

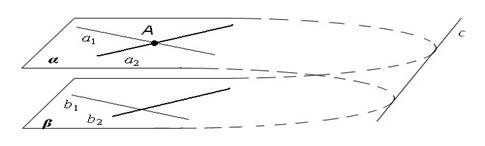
Мал. 2

Припустимо, що α і β перетинаються по деякій прямій с. Оскільки а₁ ||

b₁, то   а₁ || β, звідси   а₁ || с.  Оскільки  а₂ || b₂, то й  а₂ || β, а тому  маємо  а₂ || с.

Через точку А проходять дві прямі  а₁  і  а₂ , які паралельні прямій с, що суперечить аксіомі паралельності.

Отже, α || β.

ІІІ. Закріплення теоретичного матеріалу

1.          Відомо, що дві прямі, які лежать у площині α, паралельні двом прямим площини β. Чи випливає з цього, що α || β ?

2.          Площини α і β паралельні. Доведіть, що кожна пряма площини α паралельна площині β.

3.          Дано куб ABCDA₁B₁C₁D₁. Доведіть, що: 

а)  ABC || А₁B₁C₁ б)  AB₁D₁ || BDC₁.

4.          Точка В лежить поза площиною α. Проведіть через цю точку площину, паралельну площині α.

5.          № 20 (ст. 19). Через дану точку простору проведіть пряму, яка перетинає кожну з двох мимобіжних прямих. Чи завжди це можливо?

Розв’язання.

Нехай а і b – мимобіжні прямі (мал. 3). Проведемо площину α, через пряму а і точку М, а через пряму b і цю ж точку М проведемо площину β. Очевидно, що площини α і β перетнуться по прямій х, яка проходить через точку М (аксіома С₂). Якщо пряма х  не паралельна прямим а та b, тоді вона обов’язково їх перетинає. Отже, пряма х – шукана.

 

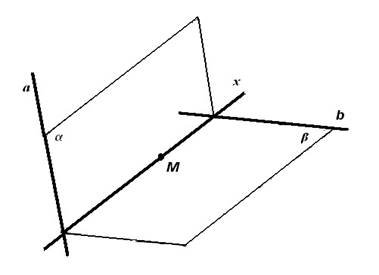
                                                              Мал. 3

У випадку, коли х паралельна одній з даних прямих (а це можливо, якщо точка М належить  площині, паралельній одній з мимобіжних прямих), задача не матиме розв’язків.

6.          Доведіть, що геометричне місце середин відрізків з кінцями на двох мимобіжних прямих є площина, паралельна цим прямим.

Розв’язання.

 

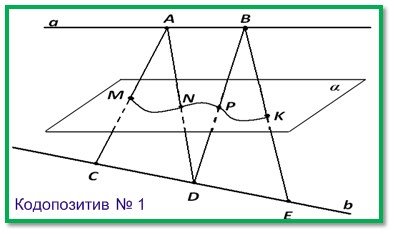
Вчитель. Нехай а і b – мимобіжні прямі. Проведемо відрізки АС, AD,

BD, BE, кінці яких знаходяться на прямих а і b (кодопозитив №1). Точки M, N, P, K є серединами проведених відрізків відповідно. Сполучимо середини цих відрізків. 

Учні. МN – середня лінія ∆ACD, NP – середня лінія ∆ABD, PK – середня лінія ∆BDE.За властивістю середньої лінії трикутника MN || CD, NP || AB, PK || DE або MN || b, NP || a, PK || b.

Вчитель. Оскільки прямі MN і NP мають спільну точку N, можна стверджувати, що вони перетинаються, і, отже, через них можна провести площину. Прямі NP і PK мають спільну точку P, тому через них також можна провести площину. MN || PK . Чому?

Учні. Згідно з ознакою паралельності прямих, з цього випливає, що через них можна провести площину.

Вчитель. Таким чином, прямі MN, NP, PK лежать в одній площині α. Аналогічно доводиться, що середини інших відрізків, які сполучають точки на прямих а і b, лежать в одній площині α.

Учні. Оскільки MN || b, то можна стверджувати, що b || α (за ознакою паралельності прямої і площини). Аналогічно а || α.

Висновок. Таким чином, площина α паралельна водночас двом мимобіжним прямим а і b. Це означає, що геометричним місцем середин відрізків з кінцями на двох мимобіжних прямих є площина, паралельна цим двом прямим, що й треба було довести.

7. Задача з кодопозитива.

                                              Задача                                  Кодопозитив № 2

Доведіть, що коли чотири прямі проходять через точку А і перетинають площину α у     вершинах  паралелограма, то     вони перетинають    будь-яку  площину, яка паралельна α і не проходить через точку

А, також у вершинах паралелограма.

 

IV. Домашнє завдання

§2, п. 10;  розв’язати наступні задачі.

Задача.  Дві сторони паралелограма паралельні площині α. Чи паралельні діагоналі паралелограма цій площині?

Задача.  Бічні сторони трапеції паралельні площині β. Чи паралельні основи цієї трапеції площині β ?

№18. Доведіть, що коли пряма перетинає одну з двох паралельних площин, то вона перетинає й другу.

№19. Доведіть, що через дві мимобіжні прямі можна провести паралельні площини.

V. Підведення підсумків уроку

1.        Як можуть розташовуватись дві площини у просторі?

2.        Які площини називаються паралельними?

3.        Сформулюйте ознаку паралельності площин.

4.        Дві сторони трапеції паралельні площині α. Як розташовані діагоналі цієї трапеції відносно площини α? Чому?

 

Тема уроку.        Властивості паралельних площин

Обладнання:      кодопозитиви, стереометричний набір.

Хід уроку

І. Актуалізація опорних знань

Дано зображення куба: варіант 1 – зліва, варіант 2 – справа.

 

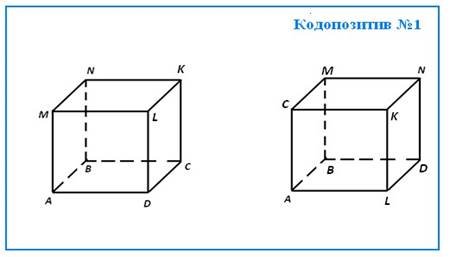
Користуючись зображенням, запишіть:

1)    площину, яка паралельна площині (АВС);

2)    паралельні площини, які містять мимобіжні прямі MK і AB;

3)    паралельні площини, які проходять через мимобіжні прямі AB і KD;

4)    площину, яка паралельна площині (MLK) і містить пряму АD.

Відповіді до тесту

	1	2	3	4
Варіант 1	MNK	ABC, KLM	ABM, CKD	ABC
Варіант 2	LNK	ABD, CKM	ABC, DKL	ABD

ІІ. Пояснення нового матеріалу

Вчитель. У кожного з вас є своя модель двох паралельних площин, які перетинаються третьою площиною. Покажіть лінії перетину цих площин. Що можна сказати про взаємне розташування цих прямих?

Доведемо таке   твердження:         якщо дві     паралельні площини перетинаються третьою площиною, то прямі їх перетину паралельні.

Доведення.

Справді, за означенням паралельні прямі – це прямі, які лежать в одній площині і не перетинаються. 

 

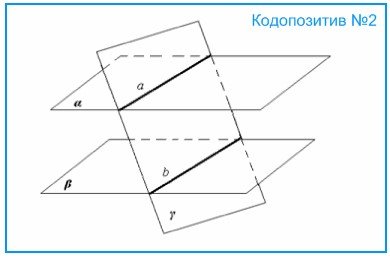
Дані прямі перетину лежать в одній площині – січній площині γ. Вони не перетинаються, оскільки за умовою не перетинаються паралельні площини α та β, які їх містять (кодопозитив № 2). 

Отже, прямі а і b паралельні, що й треба було довести.

 

Ще одна важлива властивість паралельних площин формулюється так:

відрізки паралельних прямих, які містяться між двома паралельними площинами, рівні.

 

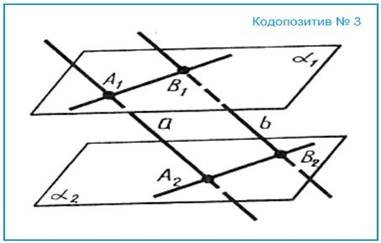
Доцільно запропонувати учням самостійно довести твердження, використовуючи готове зображення (кодопозитив № 3).

ІІІ. Розв’язування задач

1.            № 23. Площини  α і β паралельні площині γ. Чи можуть площини  α і  β перетинатися?

Розв’язання.

Робота з підручником – розібрати хід розв’язання задачі (ст. 14).

2.            Через пряму  а, яка паралельна площині  α, проведіть площину, паралельну даній площині  α. Скільки таких площин можна провести?

3.            Паралельні площини α і β перетинають сторону АВ кута ВАС відповідно у точках  А₁  і  А₂ , а сторону АС  цього кута – відповідно в точках  В₁  і  В₂. Знайдіть  АА₂  та  АВ₂ , якщо  А₁А₂ = 2А₁А,  АВ₁ = 5 см,  А₁А₂ = 12 см.

4.            Доведіть, що коли перерізом паралелепіпеда є шестикутник, то його протилежні сторони паралельні.

5.            Рівні трикутники АВС і КРТ розміщені в площинах α і β так, що прямі АК, ВР і СТ паралельні. Чи вірно, що α || β?

6.            АВСDEFA – неплоска замкнена ламана з шести ланок. Доведіть, що коли  AB || DE, BC || EF  і  CD || FA, то AB=DE, BC=EF, CD=FA.

7.            Доведіть, що два кути з відповідно паралельними сторонами  або рівні, або їх сума дорівнює 180^о.

Додаткові задачі з кодопозитивів

 

IV. Домашнє завдання

§2, п. 12;    задачі № 24 (с. 20), №32 (с. 21).

IV. Підсумок уроку

ü Сформулюйте теорему про лінії перетину двох паралельних площин січною площиною.

ü Дві паралельні площини α і β перетинаються площиною γ по прямих а і b. Вкажіть, чи правильне твердження:

-         прямі а і b можуть бути мимобіжними;

-         прямі а і b обов’язково паралельні;

-         пряма а паралельна площині β;

-         будь-яка пряма, яка лежить у площині γ, обов’язково перетинає площини α і β.

ü Сформулюйте теорему про властивість паралельних відрізків, які лежать між паралельними площинами.

 

Тема уроку.        Перпендикулярність прямих у просторі

Обладнання:      стереометричний         набір,          таблиця     «Теорема    3.1», кодопозитив.

Хід уроку І.  Актуалізація опорних знань

1.     Сформулюйте означення перпендикулярних прямих на площині.

2.     Згадайте аксіоми стереометрії. 

3.     Сформулюйте ознаки паралельності в просторі.

ІІ. Пояснення нового матеріалу

Вчитель. Поряд з відношенням паралельності в геометрії важливе значення має відношення перпендикулярності. У планіметрії ми говорили про перпендикулярність прямих. Дайте означення перпендикулярних прямих.

Учні. На площині перпендикулярними називаються прямі, які перетинаються під прямим кутом.

Вчитель.   У       стереометрії         розглядається      три    випадки перпендикулярності:

-                перпендикулярність прямих;

-                перпендикулярність прямої і площини; -    перпендикулярність площин.

На наступних уроках ми займемось послідовним вивченням вказаних випадків , і почнемо з випадку перпендикулярності прямих у просторі.

Означення. Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.

Завдання 1. Назвіть в оточенні моделі перпендикулярних прямих.

Завдання 2. Дано зображення куба. Вкажіть ребра, які будуть перпендикулярними до прямої АА₁.

Завдання 3. Задача №3 (1) з підручника (с. 34).

Вчитель. Що можна стверджувати про взаємне розташування прямих 

а₁ і  b₁, якщо  а || а₁,   b || b₁ і    а  b?

Учні висувають гіпотезу, що  а₁  b. Для ілюстрації доцільно використати каркасну модель куба або прямокутного паралелепіпеда.

Далі формулюється теорема.

Теорема. Якщо дві прямі, які перетинаються, паралельні відповідно двом перпендикулярним прямим, то вони теж перпендикулярні.

 

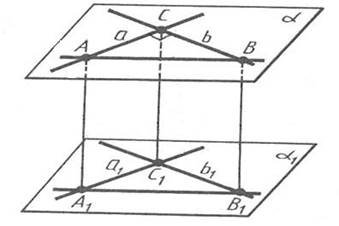
                                                            Мал. 1

Дано:  а  b,   а  α,   b  α;    а₁ || а ,   b₁ || b ,   а₁  α₁ ,   b₁  α₁ ,  а₁ і  b₁ перетинаються (мал. 1).

Довести:  а₁  b₁ .

Доведення.

Таблиця   «ТЕОРЕМА 3.1»

№ п/п	Твердження	Аргумент
1.	а і b лежать в α, а1 і b1 лежать в α1	Аксіома С3
2.	α || α1	Теорема 2.4
3.	Нехай С – точка перетину а і b, а С1 –	Означення
	точка перетину а1 і b1
4.	АА1 || СС1, ВВ1 || СС1	Теорема 2.1
5.	АА1 || ВВ1	Теорема 2.2
6.	САА1С1 і СВВ1С1 – паралелограми, тому АС = А1С1, ВС = В1С1	АС || А1С1, АА1 || СС1, ВС || В1С1, ВВ1 || СС1
7.	АА1В1В – паралелограм, тому АВ = А1В1	АВ || А1В1, АА1 || ВВ1
8.	∆АВС = ∆А1В1С1, тому кути А1С1В1 і АСВ рівні і дорівнюють 90о; отже, а1  b1	Третя ознака рівності трикутників

 

ІІІ. Розв’язування задач

1.            №1 (с. 34). Доведіть, що через будь-яку точку прямої у просторі можна провести перпендикулярну до неї пряму.

2.            Задача з кодопозитива.

 

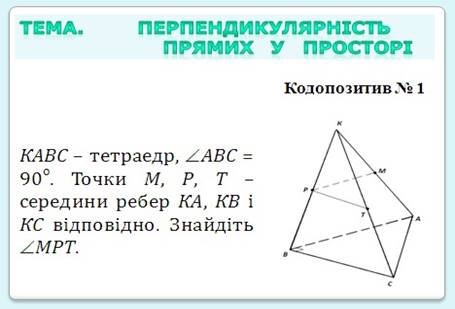
3.            №2 (с. 34). Доведіть, що через будь-яку точку прямої у просторі можна провести дві різні перпендикулярні прямі.

Доведення.

 

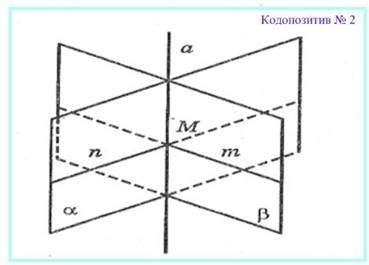
Нехай  а – дана пряма простору. Проведемо через неї дві різні площини  α і β, тоді ця пряма буде лінією їх перетину. 

Візьмемо точку М на прямій  а. Проведемо через цю точку пряму п у площині  α так, щоб  п а та пряму т у площині β,   т  а (кодопозитив №

2).

Очевидно, що через пряму  а можна провести  безліч площин і в кожній з них – пряму, що проходить через точку М, перпендикулярну до прямої  а.

IV. Домашнє завдання

§3, п. 14;   задача № 3(2, 3) (с. 34).

№3. Прямі АВ, АС і AD попарно перпендикулярні. Знайдіть відрізок СD, якщо :

2) ВD = 9 см, ВС = 16 см, АD = 5 см; 3) АВ = b , ВС = а , АD = d.

V. Підсумки уроку

1.            Які прямі в просторі називаються перпендикулярними?

2.            Чи визначають площину дві перпендикулярні прямі? Чому?

3.            Сформулюйте теорему 3.1.

 

Тема уроку.        Перпендикулярність      прямої        і         площини.    Ознака перпендикулярності прямої і площини

Обладнання:      модель куба, кодопозитиви, стереометричний набір.

Хід уроку І.  Актуалізація опорних знань учнів ü     Сформулюйте аксіоми стереометрії. 

ü   Які прямі простору називаються перпендикулярними?

ü   Сформулюйте означення паралельних прямої і площини.

ІІ. Пояснення нового матеріалу

Вчитель. Уявлення про пряму, перпендикулярну до площини дають вертикально поставлені стовпи – вони перпендикулярні до поверхні землі чи до будь-якої прямої цієї поверхні, яка проходить через основу стовпа. 

Означення. Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину і перпендикулярна до будь-якої прямої, що лежить у цій площині і проходить через точку перетину.

Вчитель. На мал. 1 пряма с перпендикулярна до площини  α.

Записується це так:  с  α. З означення випливає, що с  а   і   с  b, де  а, b  α.

 

Мал. 1

Завдання 1. Укажіть, де у своїй професії ви можете зустріти моделі прямих і площин, які перпендикулярні.

Завдання 2. Що означає твердження: пряма не перпендикулярна до площини?

Завдання 3. Чи правильно, що коли пряма не перпендикулярна до площини, то вона не перпендикулярна ні до жодної прямої, яка лежить в цій площині.

Вчитель. Як перевірити, чи перпендикулярна дана пряма до даної площини? Це питання має практичне значення, наприклад, при установці щогл, колон тощо, які потрібно поставити прямо, тобто перпендикулярно до поверхні землі.

Насправді немає необхідності перевіряти перпендикулярність прямої до всіх прямих, що лежать у даній площині  й проходять через точку перетину даної прямої і площини. 

Відповідь на це питання дає наступна теорема, що виражає ознаку перпендикулярності прямої і площини.

Теорема. Якщо пряма перпендикулярна до двох прямих, які лежать у площині і перетинаються, то вона перпендикулярна до даної площини.

Доведення.

Учні самостійно знайомляться з доведенням ознаки (с. 24). ІІІ. Закріплення набутих знань

 Дано зображення куба АВСDА₁В₁С₁D₁. Довести, що:

             а) АВ₁С₁D - прямокутник;                          б) В₁D₁  (А₁С₁С).

 Задача з кодопозитива.

Кодопозитив № 1

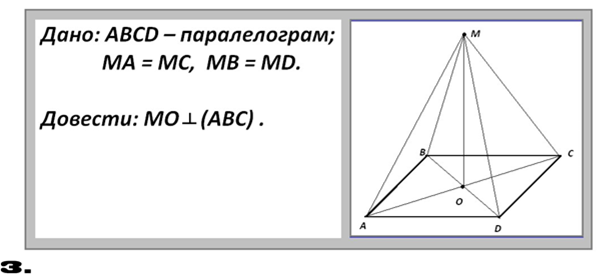 Центр описаного навколо трикутника кола проведено пряму, перпендикулярну до площини трикутника. Доведіть, що кожна точка цієї прямої рівновіддалена від вершин трикутника (мал. 2).

                                                                    

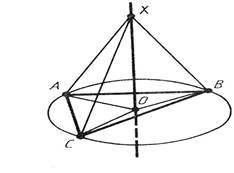
Мал. 2

 Відстані від точки М до всіх вершин квадрата однакові, точка О – центр квадрата. Доведіть, що пряма МО перпендикулярна до площини квадрата.

IV. Домашнє завдання

§3, п. 15;   задача № 5,  № 9 (с. 34-35).

№5. Доведіть, що через точку, яка не лежить на даній площині, не можна провести більш як одну пряму, перпендикулярну до площини.

№9. Доведіть, що через дану точку прямої можна провести одну і тільки одну перпендикулярну до неї площину. V. Підведення підсумків уроку

Ø   Яка пряма називається перпендикулярною до площини?

Ø   Сформулюйте ознаку перпендикулярності прямої і площини.

 

Тема уроку.        Перпендикулярні площини. Ознака перпендикулярності площин

Обладнання:      кодопозитиви, стереометричний набір, моделі куба і прямокутного паралелепіпеда. Хід уроку І. Актуалізація опорних знань учнів ü Сформулюйте аксіоми стереометрії.

ü   Які прямі в просторі називаються перпендикулярними?

ü   Сформулюйте ознаку перпендикулярності прямої і площини.

ІІ. Сприйняття нового матеріалу

Означення.        Дві    площини,    що     перетинаються,    називаються перпендикулярними, якщо третя площина, яка перпендикулярна до прямої перетину цих площин, перетинає їх по перпендикулярних прямих.

Вчитель. На кодопозитиві № 1   α  β, бо ці площини перетинаються по прямій с, а площина  γ, перпендикулярна до прямої  с, перетинає  α і β по прямих  а і b, які перпендикулярні.

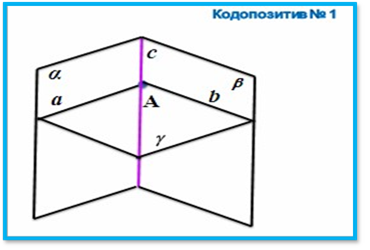
На    практиці     для    спрощення процедури визначення перпендикулярності площин використовують наступну теорему – ознаку перпендикулярності площин (кодопозитив № 2).

 

ІІІ. Закріплення нових знань

1.     Як на практиці встановити, чи перпендикулярна площина стіни до площини підлоги?

2.     № 54. Дано пряму а і площину α. Проведіть через пряму а площину, перпендикулярну до площини α.

Розв’язання.

Робота з підручником (с. 31).

3.     № 55.  

4.     № 61.  

IV. Домашнє завдання

§3,  п. 20 ;    задачі  № 59(2, 6);  № 60 (ст. 39).

V. Підведення підсумків уроку

•      Які площини називаються перпендикулярними?

•      Сформулюйте ознаку перпендикулярності площин.

•      Дано куб АВСDА₁В₁С₁D₁. Враховуючи, що ребра куба, що виходять з однієї вершини, попарно перпендикулярні, укажіть серед наведених тверджень правильні:    а) (АD₁С)  (АD₁D); б) (АD₁С) 

(СDD₁);        в) (АD₁С)  (АDС); г) (АDD₁)  (АDС).

 

Тема уроку.        Відстань між мимобіжними прямими

Обладнання:      кодопозитиви, стереометричний набір.

Хід уроку

І. Актуалізація опорних знань учнів

1.            Які дві площини називаються перпендикулярними?

2.            Сформулюйте ознаку перпендикулярності площин.

3.            Як розташована пряма, яка лежить в одній із двох перпендикулярних площин і перпендикулярна до лінії перетину цих площин, відносно другої площини?

4.            Як розташована лінія перетину двох площин, які перпендикулярні, відносно третьої площини, що перетинає їх по перпендикулярних прямих?

ІІ. Засвоєння нового матеріалу

Запитання до класу

1.     Як можуть розташовуватись дві прямі у просторі?

2.     Які прямі називаються мимобіжними?

3.     Як через одну з мимобіжних прямих провести площину, паралельну другій прямій?

4.     Чи можна через дві мимобіжні прямі провести паралельні площини?

 

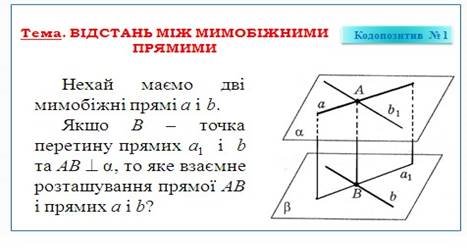
Демонструємо кодопозитив №1 і з’ясовуємо, що АВ  а та  АВ  b.

Означення. Спільним перпендикуляром до двох мимобіжних прямих називається відрізок з кінцями на цих прямих, перпендикулярний до кожної з них.

Властивість: дві мимобіжні прямі мають спільний перпендикуляр і до того ж тільки один. Він є спільним перпендикуляром до паралельних площин, які проходять через ці прямі.

Завдання. Вкажіть дві мимобіжні прямі з оточення, а також спільний перпендикуляр до цих прямих.

Завдання. Вкажіть спільні перпендикуляри до прямих АВ і СD на мал.

1

 

Мал. 1

Означення. Відстанню між мимобіжними прямими називається довжина їх спільного перпендикуляра. Вона дорівнює відстані між паралельними площинами, що проходять через ці прямі.

ІІІ. Закріплення сприйнятого матеріалу

Завдання. Кожне ребро тетраедра SABC дорівнює 10 см. Знайдіть відстань між прямими  AS і BC.

Завдання. Побудуйте спільні перпендикуляри до прямих АВ і СD на зображенні куба (кодопозитив № 2).

 

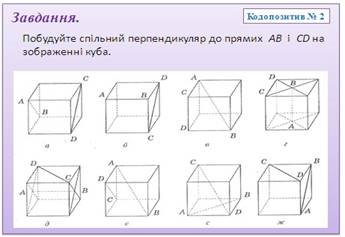
Завдання. Ребро куба дорівнює 10 см. Яка відстань між прямими а і b (кодопозитив №3).

 

Задача з несподіваною відповіддю (кодопозитив № 4).

п. 21 із §3; розв’язати задачі.

Задача. Ребро куба АВСDА₁В₁С₁D₁ дорівнює 2 см. Знайдіть відстань між прямими  АD₁ і В₁С, АВ і СС₁,  АВ і В₁D.

V. Підведення підсумків уроку

ü Що таке спільний перпендикуляр до мимобіжних прямих?

ü Сформулюйте властивість мимобіжних прямих.

ü Що таке відстань між мимобіжними прямими?

ü Чому дорівнює відстань між мимобіжними прямими?

 

 

Навчання із застосуванням інформаційних технологій є ефективним, оскільки сприяє реалізації дидактичних принципів організації навчального процесу; підвищується ефективність навчального процесу завдяки його інтенсифікації та активізації навчально-пізнавальної діяльності, надання їй дослідницького спрямування.

Доцільно використовувати комп’ютер на уроках геометрії в навчальному режимі та в режимі ілюстрування навчального матеріалу. Демонстраційні слайди, розроблені за допомогою засобів , використовуються при вивченні нового матеріалу, закріпленні його за допомогою задач, а також повторенні, узагальненні і систематизації.

 

 

 

          

III. Висновки і рекомендації

Провідним завданням шкільної освіти в умовах реалізації «Національної доктрини розвитку освіти України в ХХ ст.» і Концепції 12річної освіти є формування компетентної особистості, що передбачає створення та підтримку відповідних психолого-педагогічних умов для всебічного розвитку учнів.

Процес навчання – це процес цілеспрямованої взаємодії вчителя та учнів, під час якого учні оволодівають знаннями, уміннями, у них розвиваються здібності, формується світогляд, моральні переконання, естетичні смаки, тобто відбув освіта, розвиток і виховання школярів.

Успішність навчальної діяльності залежить від багатьох психологічних і педагогічних чинників, між тим велике знач має структура та зміст мотивів, що спонукають та спрямовують.

Наочність навчання – принцип дидактики, зумовлений характером процесу пізнання. Наочність – це не лише те, що можна бачити, а й те, що можна сприймати на слух, на дотик тощо. Наукові дослідження та апробація розробленої методики свідчать, що демонстрація, ілюстрація навчального матеріалу найдієвіше тоді, коли вони точні, коли той, хто навчається, може бачити і розуміти все, що відбувається. Всього цього не можливо втілювати в навчально-виховних процес без засобів унаочнення.

Використання наочності у процесі навчання сприяє розумовому розвиткові учнів, допомагає виявити зв’язок між науковими знаннями і життєвою практикою, між теорією і практикою, полегшує процес засвоєння і сприяє розвитку інтересу до знань, допомагає сприймати об’єкт у розмаїтті його сторін і зв’язків, стимулює розвиток мотиваційної сфери учнів.

Використання наочних посібників у навчанні має задовольняти деяким правилам: орієнтувати учнів на всебічне сприйняття предмета за допомогою різних органів чуття; звертати увагу учнів на найважливіші, суттєві ознаки предмета; показати предмет (по можливості) в його розвитку; надати учням можливість проявити максимум активності і самостійності під час огляду наочних посібників; використовувати засоби наочності стільки, скільки це потрібно, не допускати перевантаження навчання наочними посібниками, не перетворювати наочність в самоціль.

Вирішуючи проблему застосування ППЗ в процесі навчання математики, варто виходити не скільки з функціональних можливостей комп’ютера й бажання використати його в навчальному процесі, скільки з методичної системи навчання математики, аналіз якої повинен показати, які навчальні задачі можуть бути вирішені тільки ППЗ, тому що інші дидактичні засоби менш ефективні або їх застосування взагалі неможливе.

Використання ППЗ за наявності в класі проекційної техніки необхідне на етапі пояснення нового матеріалу: тут стають в пригоді презентаційні можливості інтерактивних побудов та міркувань. Доречним виявилося також застосування анімаційних ефектів під час пояснення навчального матеріалу. Головне при цьому, щоб методично правильно було продумано систему демонстрацій.

Все це в цілому сприяє розвитку важливих якостей мислення школярів: самостійності, гнучкості, критичності, глибини, раціональності. Застосовані наочні методи роботи вчителя з комп’ютерною підтримкою відкривають широкі можливості колективної, розумової, активної діяльності учнів та вчителя.

Отже, принцип наочності є одним із важливим у навчальному процесі. Багато педагогів (Бевз [7], Водовозов [20], Коменський [60], Остроградський [86], Скворцов [98], Слєпкань [99]) відзначають високу ефективність застосування засобів наочності для поглиблення інтересу учнів до навчальної і пізнавальної діяльності, для формування в них відповідних знань, умінь, навичок в сприйнятті й осмисленні оточуючого світу.

На думку досвідчених психологів (Дуткевич [33], Дьяконов [34], Дьяченко [35], М’ясоїд [80]) вища форма пізнання людиною дійсності – це абстрактне пізнання, що відбувається за участю процесів мислення та уваги. Тому дуже важливо розвивати механізми психічного відображення.

Унаочнюючи навчальний матеріал мимовільно ми створюємо середовище для діяльності пізнавальної функції психіки учня.

Наочність застосовується і як засіб пізнання нового, і для ілюстрації думок, і для розвитку спостережливості, і для кращого усвідомлення та запам’ятовування матеріалу. 

Стосовно значення принципу наочності і його ролі в процесі навчального пізнання дидактика стверджує, що наочність є вихідним моментом навчання.

Взявши це до уваги, ми розробили:

Ø Методику використання наочності при вивченні взаємного розміщення прямих і площин в курсі стереометрії.

Ø Навчально-демонстраційні     презентації із       використанням наочності.

Ø Дослідили, як розвивався принцип наочності на різних етапах становлення педагогіки.

Проведений аналіз психологічної, дидактичної та методичної літератури показав необхідність створення такої методичної системи, яка б охоплювала всі аспекти використання засобів наочності на уроках геометрії старшої школи. Вивчаючи дану методику, ми зробили висновок, що вона застосовується в структурі інших методів. Найправильніше її вважати особливим підходом до організації навчання, що виявляється перш за все в характері організації пізнавальної діяльності учнів.

Запропонована методика дозволяє вчителю здійснювати навчання учнів і допомагає виділити той спосіб організації навчального процесу, який є оптимальним для учнів даного класу, школи.

Запропонована методика використання наочності дозволить вчителю математики доцільно та ефективно використовувати різні види наочності протягом уроку, та створити необхідний комплект засобів наочності для впровадження у навчально-виховний процес. Такі дії вчителя дадуть змогу раціонально організувати навчальну діяльність учнів, робити її цілеспрямованою та продуктивною, а також реалізувати основні засади Національної доктрини розвитку освіти, а саме забезпечити подальше вдосконалення навчально-виховного процесу.

Отже, вміле використання засобів наочності в навчально-виховному процесі повинно знаходитись в руках вчителя. Він повинен у кожному окремому випадку самостійно вирішити, коли та в якій мірі треба використати наочність, адже від цього в значній мірі залежить якість знань.

 

          

IV. Список використаних джерел

1.                   Александров Г.Н. Некоторые аспекты проблемного обучения в плане умственного развития учащихся / Г.Н. Александров  Педагогика. – 1973. - №8.— с.9-10.

2.                   Алексеев В.М. Елементарна математика. Розв'язання задач / В.М. Алексеев. – К.: Вища школа, 1984. – 351 с. 

3.                   Алексеев С.В. Дифференциация в обучении предметам естественнонаучного цикла / С.В. Алексеев. – Л.: ЛГИУУ, 1991. – 112 с.

4.                   Ананченко К.О. Дифференцированный подход на уроках математики /

К.О. Ананченко, Д.Е.Пермин // Народна освіта. – 1990. – №8. – С.10-15.

5.                   Бабанский Ю.К. Оптимизация процесса обучения / Ю.К. Бабанский. – М.:

Педагогика, 1977. – 347 с.

6.                   Башмаков М.И. Уровень и профиль школьного образования / И.М.

Башмаков // Математика в школе. – 1993. - №2. – С. 8.

7.                   Бевз Г.П. Методика викладання математики: Навч. посібник / Г.П. Бевз. – К.: Вища школа, 1989. – 367с: іл.

8.                   Бевз Г.П. Методика викладання математики: Практикум / Під ред. доц. Г.П. Бевза. – К.: Вища школа, 1981. – 200 с. 

9.                   Бевз Г.П. Методика розв’язування задач: Посібник для вчителя / Г.П. Бевз.

–   К.: Радянська школа, 1988. – 192 с.

10.               Бевз Г.П. Геометрія 10-11 кл: Підручник для 10-11 класів загальноосвіт. навч. закладів / Г.П. Бевз, В.Г. Бевз, Н.Г. Владімірова. – К.: ВЕЖА, 2002. – 222с. 

11.               Березин В.Н. и др. Сборник задач для факультативных и внеклассных занятий по математике: Книга для учителя. – М.: Просвещение, 1985. – 175 с.

12.               Бобровник М.П. Наочне приладдя з математики / М.П. Бобровник, М.О. Журбас. – К.: Радянська школа, 1968. – 203 с.

13.               Болтянский В.Г. К проблеме дифференциации школьного математического образования / В.Г. Болтянский, Г.Д. Глейзер // Математика в школе. – 1988. – №3. – С.9-13.

14.               Бондар О. Значення наочності у розвитку пізнавальної активності учнів / О.Бондар // Математика. – 2001. – №7. – С. 43-44.

15.               Бондарчук О.І. Формування в учнів математичних уявлень /

О.І.Бондарчук // Радянська школа. – 1988. – №6. – С. 6.

16.               Брушлинский А.В. Психология мышления и проблемное обучение /

А.В. Брушлинский. – М., 1983. – 96с.

17.               Бурда М.І. Математика 10-11: Проб, навч. посіб. для шк., ліцеїв та гімназій гуманіт. Профілю / М.І. Бурда, О.С. Дубинчук, Ю.І. Мальований. - 2-ге вид. - К.: Освіта, 2001.-224с.

18.               Вишенський В.А. Задачі з математики. / В.А. Вишенський, М.О.

Перестюк, А.М. Самойленко. – К.: Вища школа, 1985. – 164 с.

19.               Владимиров В.С. О школьном математическом образовании. / В.С. Владимиров, Л.С. Портягин, А.Н. Тихонов // Математика в школе. – 1979.

–   №3. – С. 4-6.

20.               Водовозов В.И.   Избранные педагогические    сочинения /         В.И.

Водовозов. – М. Изд-во АПН РСФСР, 1958. – С. 251-256.

21.               Ганжела     С.      Використання      комп’ютерних      програм      на      уроках математики / С. Ганжела // Математика. – 2003. – №6. – С.15-18.

22.               Голік Л. До питання про диференціацію навчання старшокласників математики / Л. Голік // Математика в школі. – 1999. –№2. – С. 11-13.

23.               Голодюк Л.С. Рівнева диференціація на уроках геометрії / Л.С.

Голодюк // Математика. – 2003. – №39 (243). – С. 1-4.

24.               Горох О. Комп’ютер на уроці математики / О.Горох // Математика. – 2007. – №2. – С. 9-12.

25.               Горошко Ю.В. Вплив НІТ на практичну значимість результатів навчання математики в старших класах середньої школи / Ю.В. Горошко // Автореф. дис. канд. пед. наук. – К., 1993. – 24 с.

26.               Грохольська А. Виготовлення та використання кодопозитивів на уроках математики в загальноосвітній школі / А. Грохольська // Математика в школі. – 2004. – №10. – С. 12-14.

27.               Груденов   Я.Г.   Совершенствование      методики    работы        учителя математики. / Я.Г. Груденов – М.: Просвещение, 1990. – 224 с.

28.               Данилова Е.Ф. Как помочь учащимся находить путь к решению геометрических задач / Е.Ф. Данилова. – М.,1961. – 144 с.

29.               Дейкун Д.І. Диференціація навчання: Пошук оптимального варіанту /

Д.І. Дейкун // Радянська освіта. – 1990. – №35. – С. 15-17.

30.               Дидактика современной школы: Пособие для учителей / Под ред. В.А.

Онищука. – К.: Рад. школа, 1987. – 351 с.

31.               Дубравська Д.М. Основи психології: Навчальний посібник / Д.М.

Дубравська. – Львів: Світ, 2001. – 280 с.

32.               Дубровский В.Н. и др. Интерактивные стереочертежи к учебнику А.В. Погорелова, www.mto.ru/karat/index.html .

33.               Дуткевич Т.В. Загальна психологія (Конспекти лекцій): Навч. посібник / Т.В. Дуткевич. – Кам’янець-Подільський, 2002. – 96 с.

34.               Дьяконов В.П. Компьютерная математика: Теория и практика / В.П.

Дьяконов. – М.: «Нолидж», 2000. – 1296 с., ил.

35.               Дьяченко В.К. Новая дидактика / В.К. Дьяченко. – М., 2002. – 234 с.

36.               Жалдак М.І. Комп’ютер на уроках математики / М.І. Жалдак. - К.: Техніка, 1997. - 504 с.

37.               Жалдак М.І. Комп’ютер на уроках геометрії: Посібник для вчителів /

М.І. Жалдак, О.В. Вітюк. – К.: НПУ імені М.П. Драгоманова, 2000. – 168 с.

38.               Забранський В. Організація письмових самостійних та контрольних робіт при диференційованому навчанні математики / В. Забранський, Н.

Забранська // Математика в школі. – 2000. – №5. – С. 30-33.

39.               Загальна психологія / За загальною ред. акад. С.Д. Максименка. – Вінниця: Нова книга, 2004. – 704 с.

40.               Загальна психологія: Підручник / О.В. Скрипченко, Л.В. Долинська,    З.В. Огороднійчук та ін. – К.: Либідь, 2005. – 464 с.

41.               Зайцева Н. Навчальні відеофільми – опосередкована виражальними засобами наочність / Н.Зайцева // Освіта. Технікуми. Коледжі. – 2006. – №1

(14). – С. 40-45.

42.               Занков Л.В. Сочетание слова учителя и средств наглядности в обучении / Л.В.Занков. – М.: Изд-во АПН РСФСР, 1958. – 528 с.

43.               Занюк С.С. Психологія мотивації / С.С. Занюк. – К.: Либідь, 2002. – 304 с.

44.               Злоцкий     Г.В.   Широкий    спектр         средств       дифференциации

/ Г.В. Злоцкий // Математика в школе. – 1991. – №5. – С.8-11.

45.               Іванюта О.В. Розвиток візуального мислення підлітків (монографія) /

О.В. Іванюта. – Одеса, 2003. – 459 с.

46.               Інструктивно-методичний лист про вивчення математики у 2003/2004 навчальному році. // Математика в школі. – 2003. – №6. – С. 2-7.

47.               Інформаційний збірник МОН України № 22-23-24, 2008 р.

48.               Ісак Н. Диференціація та індивідуалізація навчання (з досвіду) / Н. Ісак // Диво слово. – 1998. – №3. – С. 45-49.

49.               Кабанов-Меллер Е.Н. Формирование примеров воображения в курсе черчетия / Е.Н. Кабанов-Меллер // Формирование и развитие пространственных представлений у учащихся. – М., 1964. – С. 47-54.

50.               Капиносов А.Н. Уровневая дифференциация при обучении математике в V-IX классах  /  А.Н. Капиносов  //  Математика в школе. – 1990. – №5. – С. 16-19.

51.               Каченовский М.И. Математический практикум по моделированию /

М.И. Каченовский. – М.: Просвещение, 1959.

52.               Киселев А.П. Элементарная геометрия. Книга для учителя / А.П.

Киселев. – М.: Просвещение,1980. – 286с.

53.               Коваленко В.П. Система вправ для контролю результатів навчання / В.П. Коваленко // Математика – 2000. – №31-32. – С. 7-8.

54.               Коваль Т. Комп’ютерно-орієнтовані методи навчання в процесі професійної підготовки з інформаційних технологій майбутніх менеджерів-економістів. Наукові записки Тернопільського національного педагогічного університету імені В.Гнатюка. Серія: Педагогіка. – 2007. – №6. – С. 80-86.

55.               Ковчин Н.А. Диференціація учнів за здібностями у старших класах / Н.А. Ковчин  //  Практична психологія та соціальна робота. – 1998. – №6-7.

–   С. 89-92.

56.               Колмогоров А.Н. К методике изучения темы «Параллельность и параллельный перенос» в курсе геометрии / А.Н. Колмогоров, А.Ф.

Семенович, Р.С. Черкасов. – Математика в школе, 1973. – №1. – С 4-6.

57.               Колягин Ю.М. Методика преподавания математики в средней школе. Общая методика. Учеб. пособие для студентов физ.-мат. факультетов пед. Институтов / Ю.М. Колягин, В.А. Оганесян, В.Я. Саннинский, Г.Л.

Луканкин – М.: Просвещение, 1975. – 462 с.

58.               Колягин Ю.М. Методика преподавания математики в средней школе. Общая методика. Учеб. пособие для студентов физ.-мат. факультетов пед. Институтов / Ю.М. Колягин, В.А. Оганесян, В.Я. Саннинский, Г.Л.

Луканкин – М.: Просвещение, 1980. – 368 с.

59.               Коротка Н.І. Думки з приводу оцінювання  /  Н.І. Коротка // Математика. – 2003. – №13 (217). – С.1-3.

60.               Коменский Я.А. Великая дидактика. Избр. пед. соч. / Я.А. Коменский. –

М., 1982. – Т.1. – 596 с.

61.               Концепція математичної освіти 12-річної школи // Математика в школі.

–   лютий 2002. – С. 12-17.

62.               Корінь Г.О. Доведення математичних тверджень з використанням наочності / Г.О. Корінь // Математика в школі. – 2000. – №37. – С.6-8.

63.               Коровець І. Роль та місце комп’ютера в процесі навчально-пізнавальної діяльності учнів. Наукові записки Тернопільського національного педагогічного університету імені В.Гнатюка. Серія: Педагогіка. – 2007. – №6. – С.86-90.

64.               Красуля Л. Наочність на уроках математики / Л. Красуля // Математика в школі. – 2005. – №18. – С.7-9.

65.               Критерії оцінювання навчальних досягнень учнів у системі загальної середньої освіти // Математика в школі. – 2001. – С. 7-9.

66.               Кульчинская Н.В. Ленин В.И. Философские тетради. – Полное собр. соч., т. 29 – 729 с.

67.               Кушнір І.А. Методика розв'язання задач з геометрії / І.А. Кушнір. – К.:

Абрис, 1994. – 96 с. 

68.               Леонтьев А.Н. Деятельность, сознание, личность / А.Н. Леонтьев. – М., 1986. – 369 с.

69.               Леонтьев А.Н. Проблемы развития психики. 4-е изд. / А.Н. Леонтьев –

М.: Изд-во Московского университета. – 1981. – 584 с.

70.               Литвиненко В.Н. Практикум по элементарной математике / В.Н.

Литвиненко, А.Г. Мордкович – М.: Просвещение, 1991. – 352 с.

71.               Максименко С. Взаємозв’язок навчання і розвитку / С. Максименко // Психологія. – 2004. – №1. – С. 6-7.

72.               Малафіїк І.В. Дидактика: навч. посібник / І.В. Малафіїк. – К.: Кондор, 2005. – 398 с.

73.               Марнянський І. Корисний посібник з методики математики / І.

Марнянський // Математика в школі. — 1999. — №2. – С. 3.

74.               Марнянський І. Роздуми про нові підручники математики / І.

Марнянський // Математика в школі. — 2000. — №5 – С. 5-6.

75.               Мацько Н.Д. Формування геометричних понять в учнів: Посібник для вчителя / Н.Д. Мацько. – К.: Радянська школа, 1988. – 160 с.

76.               Методика преподавания математики в средней школе. Общая методика: Учебное пособие для студентов физико-математических факультетов педагогических институтов / В.А. Лукарин, В.Я.

Санпинский.– 2-е издание, переработанное и дополненное. – М.:

Просвещение, 1980.– 380 с.

77.               Миндюк М. Б. Составление и использование разноуровневых заданий для дифференцированной работы с учащимися / М.Б. Миндюк // Математика в школе.– 1991.– №3.– С. 12-15.

78.               Морозова Д.В. Из опыта дифференцированного обучения / Д.В.

Морозова // Математика в школе. – 1998. – №6. – с. 37-40.

79.               Моторіна В.Г. Технології навчання математики в сучасній школі / В.Г.

Моторіна. –  Харків, 2001. – 262 с.

80.               М’ясоїд П.Л. Загальна психологія: Навчальний посібник / П.Л. М’ясоїд.

–   К.: Вища школа, 2001. – 487 с.

81.               Никифорова М.А. Преподавание математики и новые компьютерные технологии /  М.А. Никифорова  //  Математика в школе. – 2005. – №7. – С.16-17.

82.               Новые педагогические и информационные технологии в системе образования: Учеб. пособие для студентов пед. вузов и системы повыш. квалиф. пед. кадров / Е.С. Полат, М.Ю. Бухаркина и др.; Под ред. Е.С.

Полат. – М.: Академия, 1999. – 224 с.

83.               Ноздрачева Л.М. Наглядность при обучении решению задач / Л.М.

Ноздрачева. // Математика в школе. – 1991. – №5. – С. 15-17.

84.               Огурцов А.П. Підвищення інформативності навчального тексту засобами його наочного представлення / А.П. Огурцов, Л.М. Мамаєв, В.В. Заліщук // Нові технології навчання: Наук.-метод. Збірник. – К. : Наук.метод. центр вищої освіти, 2003. – Вип. 35.

85.               Особливості поглибленого вивчення математики в 10 класі / Навчально-методичний посібник / К.: Освіта, 1992 р.

86.               Погорєлов О.В. Геометрія: Стереометрія: Підручник для 10-11 кл. серед. шк. – 2-ге вид. / О.В. Погорєлов. – К.: Освіта, 1995. – 128 с. 

87.               Програма для вищих навчальних закладів І-ІІ рівнів акредитації.

Математика. — К., 2002. — 206с.

88.               Програма для загальноосвітніх навчальних закладів. Математика 5 – 12 класи. – К., Ірпінь: Перун, 2005. – 65 с.

89.               Програма для поглибленого вивчення математики в 10-11 класах // Математика в школі. – 2003. – №6. – С.19-25.

90.               Психологія. / За ред. Ю.Л. Трофімова. – К.: Либідь, 2005. – 506 с.

91.               Рабунский Е.С. Индивидуальный подход в процессе обучения / Е.С.

Рабунский // Математика в школе. – 1998. – №5. – С.16-18.

92.               Раков С.А. Компьютерные эксперименты в математике. Учеб. пособие для учащихся / С.А. Раков, В.П. Горох. – Х.: РЦНИТ – 1996. – 175 с.

93.               Роганін О.М. Геометрія 10 клас: Розробки уроків / О.М. Роганін. – Х.:

Веста: Видавництво «Ранок», 2008. – 240 с.

94.               Розин В.М. Логико-семиотический анализ знаковых средств геометрии (к построению учебного предмета) / В.М. Розин. – Педагогика и логика. М.: На правах рукописи, 1968. – 112 с.

95.               Рыбников К.А. К вопросу о дифференцированном обучении / К.А.

Рыбников // Математика в школе.–1998.–№5.– С. 16-18.

96.               Самовол П.И. К проблеме дифференциации обучения / П.И. Самовол // Математика в школе.– 1991.– №4. – С. 17-19.

97.               Симан С. Доводимо теореми з використанням комп’ютерної графіки /

С.Симан // Математика в школі. – 2006. – №8. – С.2-4.

98.               Скворцов І. Записки з педагогіки. Загальна дидактика / І. Скворцов. – К., 1993. – 475 с.

99.               Слєпкань З.І. Методика навчання математики. Підруч. для студ. мат. спеціальностей пед. навч. закладів / З.І. Слєпкань. – К.: Зодіак-ЕКО, 2000.

–   238 с.

100.          Слєпкань З.І. Ще раз про диференціацію навчання математики і роль в ній освітнього стандарту / З.І.Слєпкань // Математика в школі. – 2002. – №2. – С. 29-30.

101.          Слепкань З.И. Психолого-педагогические основы обучения математике: метод. Пособие / З.И. Слепкань. – К.: Рад. школа, 1983. – 192 с.

102.          Солодей Л.В. Самостійна робота учнів / Л.В. Солодей // Математика. – 2002. –№33. – С.1-4.

103.          Средства обучения математике: Сборник статей / Сост. А.М. Пышкало.

–   М., 1980. – 208 с.

104.          Сучасний урок. Інтерактивні технології навчання: Наук.-метод. посібник / За ред. О.І. Пометун. – К.: А.С.К., 2005. – 192 с.

105.          Тарасенкова Н.А. Використання знаково-символьних засобів у навчанні математики / Н.А. Тарасенкова. – Черкаси: Відлуння-ПЛЮС,

2002. – 406 с.

106.          Тарасенкова Н.А. Стереометрія 10 клас. Диференційовані завдання за готовими малюнками / Н.А. Тарасенкова. – К.: Фенікс, 1998. – 169 с.

107.          Тарасюк В.Є. Саморобні прилади з математики / В.Є Тарасюк, М.О.

Придатко. – К.: Рад. шк., 1962. – 149 с.

108.          Тесленко І.Ф. Елементарна математика. Геометрія: Навчальний посібник для фізико-математичних факультетів педагогічних інститутів. –

2-ге видання, доповнене / І.Ф. Тесленко. – К.: Радянська школа, 1968. – 318 с.

109.          Тесленко І.Ф. Елементарна математика. Геометрія: Навчальний посібник для студентів фізико-математичних факультетів педагогічних інститутів. – 3-тє видання, перероблене і доповнене / І.Ф. Тесленко. – К.:

Вища школа, 1973. – 300 с.

110.          Тимощук М.Е. О дифференцированной помощи учащимся при решении математических задач / М.Е. Тимощук // Математика в школе. – 1993. –№2. – С. 44-46.

111.          Урок математики в школі. Посібник для вчителів / Під ред. Г.П. Бевза.

–   К.: Рад. школа, 1977. – 112 с.

112.          Ушинский К.Д. Сборник сочинений / К.Д. Ушинский. – М., 1950. – Т.8.

–   776 с.

113.          Харитонова О.В. 3D STUDIO MAX на уроке стереометрии / О.В. Харитонова // Математика в школе. – 2006. – №8. – С.61-64.

114.          Цукренко С. Дидактичні матеріали / С. Цукренко // Математика в школі. – 2002. – №2. – С. 44-47. 

115.          Черних Л.В. Диференційований підхід у навчанні математики / Л.В.

Черних // Математика. – 2003. –№12 (216). – С.4-7.

116.          Шапиро И.М. Использование задач с практическим содержанием в преподавании математики: книга для учителя / И.М. Шапиро. – М.:

Просвещение, 1990. – 96 с.

117.          Швець В.О. Навчальні цілі і методика їх формування / Методика викладання математики і фізики / В.О. Швець. – К.: Рад. Іго, 1992 р.

118.          Шорох-Троцький С. Мета і засоби викладання нижчої математики з точки зору вимог загальної освіти / С. Шорох-Троцький. – М., 1992. – 358 с.

119.          Юркина С.Н. О дифференцированном обучении математики / С.Н.

Юркина // Математика в школе. – 1990. – №3. – С. 23-26.

120.          http://www.utk.mastak.ru  

121.          http://library.rehab.org.ua/ukrainian/soc/graborov1  

122.          http://www.referatka.net/index.php?action=referat&referat=3971