Позакласний захід "Подорож у світ чисел і геометричних фігур"

Подорож у світ чисел і геометричних фігур

    Сьогодні ми продовжуємо подорожувати сторінками математики. І запрошуємо наших учнів, ведучих провести нас у світ чисел  і геометричних фігур.

Глибина і абстракції сила, -

Підрахунок в задачах стрункий

Строга логіка, вигляд красивий

Математиків ваблять віки.

Проникаючи в зоряні далі,

В таємниці земної кори

Математика всіх закликає:

«Ти міркуй, фантазуй і твори!»

Якщо хочеш досягнути

У житті своїх вершин,

Математику збагнути

Мусиш тонко, до, глибин.

Калькулятор і комп'ютер

Хто сьогодні їх не знає.

Та за пояс їх заткнути

Може світла голова.

Якщо хочеш бізнесменом

Після школи, друже, стать

Аксіоми й теореми

Мусиш добре пам'ятать.

Якщо лікарем ти станеш,

То, колего, тут затям,

Коли десь ти помилився, -

Хтось поплатиться життям.

Не кажу про космонавтів,

Вчителів і моряків…

То, коли, чогось не знав ти,

Час це вивчити настав,

Не махай на все рукою,

Не лінуйся, а учись.

Бо чого навчишся в школі,

Знадобиться ще колись.

ЛІЧИЛОЧКА

Одна маленька дівчинка  

      Пішла гуляти в сад.

   Там дві зелені яблуньки

Край тину стали в ряд:

Під вітами три квітоньки,

Чотири будяки.

Над ними п'ять метеликів

Ведуть свої танки.

Шість коників змагаються —

Хто вище всіх стрибне!

А сім пташок цвірінькають, Вітаючи мене.

До тину між деревами

Драбиноньку припну.

Угору по драбиноньці

Аж вісім раз ступну.

У мене дев'ять друзів є,

Покличу їх мерщій.

І десять стиглих яблучок

Складу у кошик свій.

Смачних рум'яних яблучок

Нам вистачить усім;

Я друзям дам по одному,

Сама десяте з'їм.

        Математика – цариця наук. Це дуже древня наука. Ще багато років до нашої ери Архімед, Евклід, Піфагор та багато інших вчених виводили та користувалися формулами, які ми сьогодні вивчаємо та використовуємо на практиці. Розвиваючи спостережливість і закономірність природніх явищ, ще древні єгиптяни, вавилоняни та інші народи  стародавнього сходу за 200 років до н. е. знали, що трикутник із сторонами 3, 4, 5 – прямокутний. Такий трикутник називали єгипетським. Теорема Піфагора була відома ще вавилонянам, ще за 1200 років до Піфагора, який дав перше повноцінне доведення цієї теореми. Слово «симетрія»  -

Грецького походження, що означає правильне відношення. У геометрію елементи вчення  про симетрію  ввів французький вчений  А. М. Лежандр (1752 – 1833).

        Математик, так само, як художник, або поет  створює візерунки, і якщо ці візерунки більш стійкі, то лиш тому , що вони складені з ідей. А зараз просимо повідомити нам. Як пов'язана  математика з мистецтвом.

Математика і мистецтво

    Г. X. Харді (Наrdіу С. Н. Маthematic'lans аро1оgу. Саmbridge. Аt the university press. 1944) писав: «Математик так само, як художник або поет, створює візерунки. І якщо ці візерунки більш стійкі, то лиш тому, що во­ни складені з ідей... Візерунки математики так само, як візерунки худож­ника чи поета, повинні бути прекрасні; ідеї так як кольори або слова, по­винні гармонійно відповідати одна одній. Краса -  є перша вимога: у світі немає місця для некрасивої математики». Довжини трьох струн, які дають ноти до, мі, соль, що складають мажорний акорд, відносяться як числа , а число коливань цих струн — як , або 4: 5: 6, причому 6-5=5-4. Приємна для слуху співзвучність підкоряється простим математич­ним законам.

     Ще піфагорійцями була створена математична теорія музики. Створення логарифмічно рівномірної 12-тональної музичної шкали — результат спільної діяльності музикантів і математиків. Вона могла з'явитися тільки після розробки загальної теорії відношень і теорії лога­рифмів у XVII ст. Не випадково протягом усього цього століття в теорії зберігалась точка зору на музику як на науку про числа, тобто як на роз­діл математики.

     У листі до Гольбаха від 17 квітня 1712 р. Лейбніц дає таке знамени­те означення музики: «Музика є арифметична вправа душі, яка рахує се­бе, не знаючи про це».

     У XVIII ст. створюється музична акустика. Математики Л. Ейлер, і

 Д. Бернуллі, Ж. Даламбер розробляють повну теорію коливань струни.

Як виникло слово «математика»?  Слово «математика» виникло у Давній Греції десь у VI ст. до н. е. і походить від грецького «марема»  -  знання, вчення. Цих знань було чотири: про числа, про фігури,  світила і музику. Знання були священні, відомі тільки невеликому колу людей -  жерцям у храмах та їх учням.  Ніхто з них не мав права ділитися цими знаннями з посторонніми людьми. За спробу стати жерцем поплатився не один претендент. Як свідчать ієрогліфи , знайдені під час розкопок, на стінах давньоєгипетського храму,  таку людину замуровували в одному із приміщень храму. Де знаходилась певна практична задача. Якщо її вдавалось розв'язати, то відповідь кидали крізь щілину в стіні. Жерці перевіряли відповідь. Якщо відповідь правильна. Тоді ти вийдеш жерцем ради, якщо ж відповідь не правильна – то голод переможе твоє тіло. «Думай – цінуй своє життя», - написано на стінах храму.

       Відомий давньогрецький учений Піфагор, теж був жерцем, і навіть не показувався своїм учням. А навчав прикриваючись запоною. Вперше математиками назвали тих послідовників Піфагора, які до повчань свого вчителя наважились додавати і свої міркування. Отже – слово «математика» набуло змісту – «знання – одержані через роздуми».

       А чи знаєте ви, як виникли перші числа?  Як називаються  числа якими ми користуємось і звідки походять? Що ж за числа дивні? Попросимо розповісти нам.

        Першими записами чисел можна вважати зарубки на стовбурах дерев, палицях

чи кістках. Але великі числа зображати таким способом було не зручно. Риски почали об'єднювати зверху дужками по5,10, 12 , і навіть по 60… Так виникли значки для груп чисел – ієрогліфи. Дивіться запис числа 2326 Давній Єгипет 5 тис. років до н. е. (дод. – слайд)

     …Через арабів, які завоювали Індію, ці числа (індійські) почали повільно проникати в Європу (протягом  XII – XVII ст.) і дістали назву – арабські. Лише 200 років тому, дуже зручну індійську нумерацію стали використовувати в усьому світі. Величезна заслуга індійських математиків і в розвитку вчення про звичайні дроби, хоча їх знали ще давньоєгипетські та вавилонські  математики; і майже за 2 тис. років до н. е. древні греки. А ось працю про десяткові дроби та дії над ними вперше було написано по- сусідству з Індією. Це зробив середньо азіатський вчений – Кані (Самарканд).

Тепер вже будемо знати. Як називаються числа, які ми використовуємо при лічбі та запису – це арабські числа. А зараз розповідь для майбутніх будівельників.

Про пропорції людини

     Вітрувій,  древній зодчий,  якому римляни доручали великі будови, говорив: «Хто хоче будувати, той повинен орієнтуватися на будові люд­ського тіла, тому що в ньому знайдете сховані таємниці пропорцій. І тому, перш ніж почати будівництво, я хочу розповісти, якими повинні бути добре складені чоловік, жінка, дитина, кінь. Таким чином ти зможеш лег­ко знаходити міри всіх речей».

     Тому послухайте, що спочатку говорить Вітрувій про пропорції людського тіла, яким він навчився у великих прославлених живописців та майстрів лиття. Вони говорили, що людське тіло таке: обличчя від підбо­ріддя доверху чола складає десяту частину людини. Таку довжину має витягнута долоня. Голова ж людини складає восьму частину тіла. Якщо поділити обличчя на три частини від волосся до підборіддя, то у верхній буде лоб, у другій — ніс, у третій — рот. Ступня складає шосту частину тіла людини.

     На подібні частини він ділить і будівлі і говорить: якщо покласти на землю людину з розкинутими ногами і руками та поставити ніжку цирку­ля в пуп, то коло буде дотикатися рук і ніг. Таким чином, він виводить круглу будівлю з пропорцій людського тіла.

     І подібним чином будують квадрат: якщо поміряти довжину від ніг до маківки, то ширина розкинутих рук буде дорівнювати цій довжині. Звідки він виводить квадратні будови. 

      А зараз перенесемось до Древнього Єгипту, тому будьмо уважні і послухаємо цікаву легенду про Фалеса.

      З ім'ям Фалеса пов'язано багато легенд. Проте немає ніяких сумнівів,що він був великим вченим. Його було зараховано до групи так званих «семи мудреців».

      За переказами Фалес, за наказом єгипетського фараона Амазиса, виміряв висоту піраміди  Хеопса. В ясний сонячний день,він накреслив навколо себе коло, радіус якого дорівнював його зросту. Коли кінець тіні Фалеса впав на це коло, тобто ,коли довжина тіні стала дорівнювати зросту Фалеса, він швидко попрямував до того місця, де була тінь від вершини піраміди і поклав там камінь.

Фалес справедливо вважав, що в цей час тінь від піраміди дорівнює висоті самої піраміди. Додавши до довжини тіні половину довжини основи, Фалес знайшов висоту піраміди. В школі ми вивчаємо відому теорему Фалеса.

     Тут зробимо невеличкий ліричний відступ, і послухаємо уривок «Енеїди»  І. П. Котляревського.

Еней, герой уславленої «Енеїди» І. П. Котлярев­ського, зазнавши численних морських пригод, приплив нарешті до берега і подався у місто.

  …Еней прочумався, проспався ,

І голодранців позбирав,

За всім зібрався і уклався,

І скільки видно, почухрав.

Плив – плив,  плив – плив,

Що аж набридло,

І море так йому огидло,

Що бісом на нього дививсь:

«Коли б, - каже, - умер я вТрої,

Уже б не пив сеї гіркоїї

І марно так не волочивсь».

Потім до берега приставши

З троянством голим всім своїм,

На землю з човнів повстававши,

Спитав, чи є що їсти їм,

І зараз чогось попоїли,

Щоб на путі не ослабіли,

 Пішли, куди хто запопав.

Еней по берегу попхався,

І сам не знав куди слонявся,

Аж гульк, і в город причвалав.

В тім городі жила Дідона,

А город звався Карфаген,

Розумна пані і морна

Для неї трохи сих імен:

Трудяща,  дуже працьовита,

Весела, гарна, сановита…

     Як розповідає легенда, близько 825 р. до н. є. фі­нікійська царівна Дідона з невеликим загоном воїнів, шукаючи щастя, обрала зручне місце на північному уз­бережжі  Африки  (нинішня  Туніська  затока).   Король Нумідії, Ярб погодився продати їй ділянку землі, але «не більше, ніж можна обмежити шкірою бика». Дідона не розгубилася. Вона розрізала шкіру на тоненькі смуж­ки і, зв'язавши з них ремінь довжиною l, обмежила ді­лянку найбільшої площі. Так був заснований город Карфаген, першою легендарною правителькою якого стала Дідо­на.

Дідона мала кілька варіантів вибору ділянки, а саме: 

 а) прямокутник  максимальної  площі;

 б) прямокутний трикутник максимальної площі;

 в) фігуру мак­симальної площі довільної форми.

Розглянемо результати одер­жала б Дідона для цих варіантів?

      Нехай а і b — довжини сторін прямокутника. То­ді   , а  вираз для обчислення площі цього прямокутника отримаємо з формули

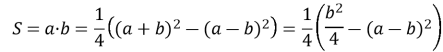
 З одержаного співвідношення видно, що площа прямо­кутника буде максимальною, коли  і він стає квад­ратом. Тоді Тим самим доведено, що з усіх прямокутників з периметром   l   найбільшу площу має квадрат.

       Дідона, напевне, скористалася тим, що вибирала ді­лянку на березі моря і використала берегову лінію, моря як одну із сторін прямокутника. Тоді вираз для обчислення площі набуде вигляду:  
.

 Площа набирає максимального значення, якщо тобто при   і    і дорівнює  .  При такому варіанті площа стає вдвічі більшою.

      Серед усіх трикутників з двома даними сторонами  а і b найбільшу площу (що дорівнює    l²/8) має той, у якого ці сторони взаємно перпендикуляр­ні. А серед усіх прямокутних трикутників з даною сумою катетів найбільшу площу має рівнобедрений три­кутник.

      Найбільшу площу на березі моря можна обме­жити півколом з радіусом   ця площа дорівнює  .

       А зараз запрошую вас розгадати «Математичні загадки».

1. Що за числа дивні,

 їх нема на гривні,

Але часом є в книжках,

Дехто носить на руках.      (римські)

2. Перед нами є пряма

Середини в ній нема

А як на ній покладем точку

Вийдуть рідні два браточки,

Що побігли в два кінці,

А зовуться?...                        (промені)

3. ой велика в нас держава,

Як вмістити все на карті?

Змалювать поля з лісами,

Гірських масивів ряд

Допоможе нам… .           (масштаб)

4. З точки А у два кінці

 два побігли промінці.

Чи точніше – промені

Дві фігури нам дають

Кожна має назву?......         ( кут).

5. Все розкажуть нам науки

Скільки важить кит,чи щука?

Коли землі відкривали,

Та коли де воювали…

пам'ятати роки й грами

нам поможуть?.....             (діаграми).

6. Я променя сестра,

чи часточка прямої,

І числа на мені  -

 для користі людської

та коли на вазі

То малюють по дузі.

Я на приладах мала,

Всі зовуть мене?......              (шкала)

7. А ми на листочку

не вряд ставим точки

Можна три, а краще  - п'ять

Коли А із В з'єднать, В із С,

а С із D…

Що тоді у нас буде?......     (ламана)

8. Зараз віршик про кути,

Що шкідливі мов коти:

То штани вони порвуть,

А то й носа розіб'ють.

Скрізь кути, кути , кути –

Їх ніяк не обійти.

Який з них виділяється

частіше зустрічається?......  (прямий).

І прямуючи до завершення нашої подорожі пропонуємо вашій увазі цікаві задачі.

 В.:    (11, 22, 33, 44….) 

  В.:    (1, 2, 3)

 В.:    ( Перше будь-яке, а друге 1)

 В.:    ( На 0 ділити неможна)

«Математичні жарти»

    Коли невстигаючого учня викликали до дошки то він, аби стовпом не стояти з горя почав писати відповідь у стовпчик зверху вниз: «Раз не знаю, два не знаю,….». Потім, дійшовши так до кінця, у розпачі написав ще й знизу вгору: «Раз не знаю, два не знаю,….». І був дуже здивований,коли йому всі закричали –

«Знає! Знає!»

9

9

9

9

9

9

9

9

Часто можна почути запитання:

-         А що таке точка?

-         Точка і пряма не мають означення в геометрії.

-         Ні, мають! Точка – це кут у якого відірвали сторони, а пряма – це точка, яка побігла.

         Ось на такій веселій ноті завершуємо нашу подорож. Як бачимо математика дуже цікава наука, зустрічається майже всюди у повсякденному житті, тому навіть найпростішими теоремами, формулами не треба нехтувати, бо, як розпочинали ми нашу мандрівку: «… чого навчишся в школі, Знадобиться ще колись». Або ж словами Піфагора: «Не роби ніколи того, що не знаєш. Але вчись усьому, що потрібно знати, і тоді будеш вести спокійне життя».      

           Дякуємо за увагу!