Позакласний захід з математики "Цікава математика"

Позакласний захід з математики

 

 

«Цікава математика»

 

для учнів 8-х класів

 

 

вчитель: Свинцицька Л.В.

 

 

 

 

 

 

Позакласний захід для 8–х класів.

Тема: розв'язування логічних задач і задач на кмітливість.

Цілі: 1. Розвиток інтелекту учнів.

2. Розвиток пізнавальної та творчої діяльності учнів.

3.Виховувати любов до математики через ігрові форми роботи.

Форма заняття: дидактична гра.

Обладнання: таблиці, картки, паперові стрічки, клей, ножиці, питання на слайдах.

Хід гри.

I етап. Організаційний момент.

ІІ етап. Розминка.

Назвіть прислів'я з натуральним числом (переможець той, хто назве останній).

ІІІ етап. Математичні обгонялки.

1) Як називаються координати x і y? (Абсциса і ордината.)

2) У китайських математиків у 2 столітті до нашої ери одні числа витлумачувалися як "майно", а інші як "борг". Назвіть ці числа.

(Позитивні і негативні)

3) Трійка коней пробігла 30 км. Яку відстань пробіг кожен кінь? (30 км)

4) Яку математичну задачу вирішує свиня, коли підриває кущ картоплі? (витягує корінь)

5) Два в квадраті – чотири, три в квадраті – дев'ять. Чому дорівнює кут в квадраті? (90)

6) Обчисліть 162 - 152 (31)

7) Буває трикутник з двома тупими кутами? (немає)

8) Назвіть найбільше число, що складається з різних цифр. (9876543210)

9)Який чотирикутник схожий на «спідничку»? (трапеція) 10) Чому дорівнює сума кутів в трикутнику? (180)

11) чи Правда, що якщо в трикутнику один з кутів дорівнює 1200, а інший 600? (ні)                                                                                       12) Як називається промінь, який виходить з вершини кута і ділив кут навпіл? (бісектриса)                                                                          13)Чому дорівнює площа квадрата зі стороною 1 метр? (1м²)

14) Площа прямокутника дорівнює... (s=a*b)

IV етап. Чарівний квадрат. ( Магічний квадрат)

1) Розставте цифри так, щоб сума цифр була 15 по горизонталі, вертикалі і діагоналі.

 

4	9	2
3	5	7
8	1	6

 

 2) Розставте цифри так, щоб сума цифр була одна і та ж по горизонталі і вертикалі.

 

1	1	1
2	2	2
3	3	3

2	3	1
1	2	3
3	1	2

                                                                  Відповідь:

 

 

 

Числа від 1,2, ..., n повторюються в кожному рядку і в кожному стовпці. Такий квадрат називається латинським квадратом.

3) Не відриваючи олівця від паперу, розділити фігуру на 6 рівних трикутників

 

                                   Відповідь: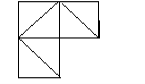                    

   

V етап. Математичний єралаш

(вважай, смекай, відгадуй)

1. Що більше, твір або сума чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9?

(Більше сума, так як добуток дорівнює 0)

2. Знайти: 1 + 2 + 3 +...+ 98 + 99 + 100

Історію рішення цієї задачі.

− Цю задачу вирішив у XVIII столітті хлопчик Карл Гаусс, якого згодом стали називати " Королем математики. Він зауважив, що в запису 1 + 2 + 3 + ... + 98 + 99 + 100 сума кожної пари доданків, які однаково відстоять від кінців записаного виразу, що дорівнює 101. А таких пар в два рази менше, ніж доданків, тобто 50.

Виходить сума дорівнює 101•50 = 5050.

 

VI етап. «Решето Ератосфена»

Якими бувають числа?

Просте число — це натуральне число, яке має рівно два натуральних дільника (тільки 1 і самого себе). Всі інші числа, крім одиниці, називаються складеними. Таким чином, всі натуральні числа більші одиниці розбиваються на прості і складові.

У III столітті до нашої ери Олександрійський учений Ератосфен вказав спосіб отримання послідовності простих чисел, відомий нині як «Решето Ератосфена»

Запишемо числа по шість в рядок, як показано в таблиці.

 

1	2	3	4	5	6
7	8	9	10	11	12
13	14	15	16	17	18
19	20	21	22	23	24
25	26	27	28	29	30
31	32	33	34	35	36
37	38	39	40	41	42
43	44	45	46	47	48
49	50	51	52	53	54
55	56	57	58	59	60
61	62	63	64	65	66
67	68	69	70	71	72
73	74	75	76	77	78
79	80	81	82	83	84
85	86	87	88	89	90
91	92	93	94	95	96
97	98	99	100	101	102

Спочатку викреслимо всі парні числа, крім двійки, це три стовпчики з жовтим фоном. Потім викреслимо числа кратні трьом крім самої тройки - це блакитний стовпчик. Стовпчик під шісткою вже викреслений як парний.

Тепер позбавляємося від чисел, кратних п'яти, проводячи сині пунктирні лінії, втім, треба буде відзначити тільки 25,35,55,65,85 і 95, так як інші числа викреслені раніше.

Також робимо і з 7 - проводимо рожеву пунктирну лінію, викреслюючи залишилися 49,77 і 91.

Більше нічого не треба викреслювати числа кратні 8, 9 і 10 викреслені при видаленні відповідно парних і кратних трьом.

Залишилися числа і є всі прості числа, менші 100, або, точніше, 102, раз вже це число виявилося в таблиці

 

                         Строго упорядкований алгоритм решета Ератосфена наводить на думку, ніби можна знайти формулу, що дозволяє хоча б вказати точне число простих чисел на будь-якому інтервалі числової осі, - справа не таке вже важке. Але скільки не билися математики, їм так і не вдалося знайти бажану формулу.

Чому «Решето»?

Так як за часів Ератосфена писали на воскових табличках і не викреслювали, а "виколювали" цифри, то табличка після описаного процесу нагадувала решето. Тому метод Ератосфена для знаходження простих чисел отримав назву "решето Ератосфена".

Завдання для команд.

Учням видають таблиці, в яких треба закреслити складені числа і вибрати прості.

 

103	104	105	106	107	108
109	110	111	112	113	114
115	116	117	118	119	120
121	122	123	124	125	126
127	128	129	130	131	132

 

VII етап. Цікаві числа

Число 37 володіє багатьма цікавими властивостями.

37 × 3 = 111                                     37 х 18 = 666
37 × 6 = 222                                     37 х 21 = 777 
37 × 9 = 333                                     37 х 24 = 888
37 ×12 = 444                                   37 х 27 = 999
37 × 15   = 555

     Так, помножене на 3 і на числа, кратні 3 (до 27 включно), воно дає твори, зображувані однією якою-небудь цифрою.

Обчислимо:

1) добуток числа 37 на суму його цифр

37 × (3 + 7) = 370

2)суму кубів тих же цифр

2) 33 + 73 = 370.

3) Із суми квадратів його цифр відняти добуток тих же цифр

(32 + 72) – 3×7 = 37

 

Але чи не найбільш цікавою властивістю числа 37 є те, що деякі кратні йому числа при круговій перестановці входять до них цифр дають знову-таки числа, кратні 37.

Наприклад: 259 = 7 × 37

                   592 = 16 × 37
                   925 = 25 × 37

VIII етап. Неймовірно, але факт.

Помнож свій вік на 7, а потім — на 1443, то результат Тебе неодмінно здивує.

— Ти отримав свій вік, написаний три рази поспіль.

 

ІХ етап. Дивовижні властивості листа Мебіуса.

Август Фердинанд Мебіус 1790-1868

Німецький геометр народився в місті Шульпфорте.

Професор Лейпцігського університету з 1816 року.

Встановив існування односторонніх поверхонь (1858р.), одна з яких - лист Мебіуса.

Легенда

Розповідають, що відкрити свій «лист» Мебиусу допомогла служниця, яка зшила якось неправильно кінці стрічки.

Захоплююче дослідження

Запасіться кількома листами звичайного білого паперу, клеєм і ножицями.

Експерименти

1) Беремо паперову стрічку АВСD. Прикладаємо її кінці АВ і СD один до одного і склеюємо. Так, щоб точка А збіглася з точкою C, а точка B з точкою D.

2) Отримаємо таке перекручене кільце

3) Задамося питанням: Скільки сторін у листа Мебіуса?

4) У нього ОДНА сторона.

5) (Учениця показує і пояснює експеримент)

− Дивіться, я беру паперову стрічку, розділену по ширині навпіл пунктирною лінією. Я перекручую стрічку один раз і кінці склеиваю. Вийшов знаменитий лист Мебіуса. А тепер я ріжу ножицями склеєну стрічку посередині, вздовж пунктирною лінії. Як ви думаєте, що у мене вийде? Звичайно, якщо б я не перекрутила стрічку перед склейкою, все було б просто: з одного широкого кільця вийшло б два. А що зараз? Вийшло не два кільця, а одне, вже вдвічі, але зате вдвічі довше.

Практичне заняття для всіх.

а) Візьміть паперові стрічки, клей і ножиці. Приготуйте листи Мебіуса і проведіть експеримент, про який я вам розповів. Зробіть кільце, перекручене двічі. Розріжте його по середині.

Висновок: Отримали два зчеплених один з одним кільця, кожне з яких двічі перекручено.

Ось такі несподівані речі відбуваються з простою паперовою смужкою, якщо склеїти з неї лист Мебіуса.

б) Тепер зробіть новий лист Мебіуса і скажіть, що буде, якщо розрізати його уздовж, але не посередині, а ближче до одного краю?

в) А якщо розділити на три частини?

Отримаємо два зчеплених кільця. Одне з них вдвічі довше вихідного і перекручено два рази. Друге - лист Мебіуса, ширина якого втричі менше, ніж у вихідного.

г) Якщо стрічку перекрутити два рази

Отримаємо два кільця з двома перекрутами, зчеплені один з одним.

 

Вивченням таких властивостей займається наука топологія. Поняття і теореми топології корисні у всіх областях математики, техніці, економіці, психології, мистецтві. Топологія – одна з наук, в яких не вирішено багато проблем. Вони чекають на вас. Бути може, хтось внесе свій внесок в її розвиток.

  

X етап. Застосування

1) Смуга стрічкового конвеєра, виконана у вигляді листа Мебіуса, дозволяє йому працювати довше в два рази

2) У матричному принтері фарбувальна стрічка має вигляд листа Мебіуса

3) Наша Всесвіт цілком ймовірно замкнута в стрічку Мебіуса

4) Є гіпотеза, що спіраль ДНК сама по собі теж є фрагментом стрічки Мебіуса

5) Фізики стверджують, що відображення в дзеркалі

засноване на властивості стрічки Мебіуса

 

X I етап. Пам'ятки архітектури.

 

ХІІ етап. Підсумок заняття.

Нагородження переможців гри