Позакласний захід. Конференція. "Піфагор та його знаменита теорема"

Позакласний захід

Конференція

Тема.   Піфагор та його знаменита теорема

 

Мета:

• поширити знання учнів з історії математики, систематизувати знання про одну з відоміших теорем Піфагора та методи її доведення;
• логічне розвивати мислення, виховувати вміння обґрунтувати,
• чітко висловлювати свої думки, поважно ставитись до доповідача, коректно ставити запитання, сприяти формуванню інтересу учнів до математики.

 

Обладнання: проектор, екран, слайди.

 

Хід конференції

Теорема Пифагора

Если дан нам треугольник

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим —

И таким простым путем

К результату мы придем.

И. Дырченко

 

Учитель повідомляє тему та план конференції.

 

План.

І. Доповіді учнів.

1. Піфагор. Сторінки життя.

2. Теорема Піфагора (доведення з використанням означення косинуса).

3. Теорема Піфагора (доведення з використанням подібності трикутників).

4. Доведення теореми Піфагора методом площ.

5. Доведення Евкліда.

6. Доведення Леонардо да Вінчі.

ІІ. Обговорення.

ІІІ. Вікторина «Чи вірите ви, що…»

 

І. Виступи учнів. (cупроводжуються сйдовим показом малюнків, необхідні записи виконуються на дошці. Інколи слухачам пропонується закінчити доведення теореми.)

 

ІІ. Обговорення.

Питання для обговорення:

Як пояснити вислів: « Пифагоровы штаны на все стороны равны»?

Який спосіб доведення ви вважаєте більш цікавим, чому?

У чому, на ваш погляд, є унікальність теореми Піфагора?

 

ІІІ. Вікторина «Чи вірите ви, що…»

 

1. Піфагор брав участь у кулачному бої на 58 Олімпіаді, яка проходила в 548 році до нашої ери?   (Так, він був чемпіоном з цього виду спорту і зберіг титул ще на кількох олімпіадах)

2  . Теорему Фалеса назвали «міст осла»?   (Ні, так називали теорему Піфагора. Учні, які вчили теорему напам’ять без розуміння і були названі «ослами», не могли перебороти теорему Піфагора, яка була для них наче недоступний міст)

3.   Будь-який прямокутний трикутник називається єгипетським?   (Ні, тільки такий прямокутний трикутник, сторони якого пропорційні числам 3, 4, 5) 

4.   Якщо в прямокутному трикутнику один із гострих кутів дорівнює 35 градусів, то другий кут дорівнює 145 градусів?   (Ні)

5.   У прямокутному трикутнику гіпотенуза може бути меншою за один із катетів?   (Ні)

Піфагор був філософом і написав роботи з філософії? (Так, йому належать три роботи: «Про виховання», «Про державу» і «Про природу»)

6.   Такі слова належать Піфагору: «Дайте мені точку опори, і я переверну Землю»?   (Ні, ці слова належать давньогрецькому математику, фізику, астроному та інженеру – Архімеду).

7.   Чи належать ці слова Піфагору: «Не потрібна там зброя, де є мудрі закони»?   (Так, ці слова із проповіді , із якою Піфагор виступав у Кротоні)

8.   .Якщо в прямокутному трикутнику бісектриса прямого кута дорівнює половині гіпотенузи, то цей трикутник рівнобедрений?   (Так, тому що бісектриса є медіаною)

9.   Ковалевська С. В. казала: «Коли Піфагор відкрив свою знамениту теорему, він приніс у жертву богам 100 биків. З тих пір усі скоти бояться нового!»   (Так, це була відповідь Ковалевської С. В. Петербурзькому чиновнику на відмову дозволити їй викладати в університеті)

О теореме Пифагора

(Перевод А. Хованского)

Уделом истины не может быть забвенье,

Как только мир ее увидит взор;

И теорема та, что дал нам Пифагор,

Берна теперь, как в день ее рожденья.

 

За светлый луч с небес вознес благодаренье

Мудрец богам не так, как было до тех пор.

Ведь целых сто быков послал он под топор,

Чтоб их сожгли как жертвоприношенье.

 

Быки с тех пор, как только весть услышат,

Что новой истины уже следы видны,

Отчаянно мычат и ужаса полны:

Им Пифагор навек внушил тревогу.

Не в силах преградить той истине дорогу

 Они, закрыв глаза, дрожат и еле дышат.

                                                 А. фон Шаміссо

 

ІV. Підводяться  підсумки вікторини.

Нагороджуються переможці. Учитель підводить підсумки.

Слово вчителя:

Сьогодні ми доторкнулися ще раз до цікавого світу – світу геометрії. Я дякую усім учасникам конференції і бажаю вогника в очах, натхнення, цікавих досліджень.

«Вдохновение нужно в геометрии не меньше, чем в поэзии,» - казав Олександр Сергійович Пушкін.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 1

 

ПІФАГОР

 

Легендою і джерелом дискусій Піфагор став уже в стародавні часи. У 306 році до н. е. йому, як найрозумнішому з греків, поставили пам'ятник у римському форумі.

Перекази про Піфагора дають змогу намалювати правдивий образ цієї дивовижної, складної і водночас суперечливої людини.

Народився Піфагор на о. Самосі, біля узбережжя Малої Азії. Його батько Мнєсарх зі знатного, але збіднілого роду, був каменерізом. Як і інші великі греки, Піфагор здійснив традиційну подорож до Єгипту, де жив близько 22 років і витримав немало випробувань, перш ніж жерці Мемфіса і Діосполіса відкрили йому "дивовижне чергування чисел, хитромудрі правила геометри, науку про зорі, медицину". Переказують, що він побував і в Індії, де спілкувався з брахманами, від яких засвоїв не лише філософію, зокрема вчення про переселення душі, а й секрети вправ для тіла.

Повернувшись до Греції, Піфагор оселився на півдні італійського півострова в полісі Кротоні. Його появі передували чутки про зроблені ним чудеса, а його виступи перед кротонцями були першими кроками на шляху досягнення моральної і політичної влади.

Незабаром навколо Піфагора згуртувалися однодумці, організувавши аристократичний за духом, таємний релігійно-політичний союз-гетерію. Незабаром і в інших полісах південної Італії та Греції виникли піфагорійські гетерії, у яких поряд з науковими проблемами - математичними, філософськими, етичними — розглядалися релігійні і політичні.

Піфагорійський союз складався з акусматиків і математиків. Перші лише слухали загальні істини і не бачили самого вчителя. Другі, пройшовши випробування мовчанням, діставали право висловлюватися і засвоювати вчення.

Боротьба, яка точилася в еллінському світі проти панування аристократії, захопила й піфагорійців. Коли ж перемогли консерватори, це викликало обурення народу і визначило результат боротьби. Піфагорійці зазнали поразки. Рятуючись від небезпеки, Піфагор переселив­ся в Метапонт, але тут теж неспокійно, і в одній з нічних сутичок він загинув. Інших піфагорійців спіткала така сама трагічна доля.

Піфагорійське вчення - окремий випадок формування філософії, в якій міфологічні погляди під впливом математики еволюціонували в наукові.

Анархії і беззаконню піфагорійці протиставляли царство законів, справедливість влади богів.

Піфагор посідає почесне місце в історії математики. Він відкрив нову епоху в еволюції наукової думки. Піфагорійці перетворили давно відомі практичні правила в наукові положення, обґрунтовані точними доведеннями.

Піфагор увів загальновизнаний нині дедуктивний метод.

Основним змістом піфагорійської математики є вчення про число. Як і вавилонські маги, піфагорійці вважали надзвичайно важливими різні властивості чисел і відношення між ними.

Піфагорійці вважали унікальними такі числа, у яких сума власних дільників, менших від самого числа, дорівнює самому числу. Такі числа називали досконалими.

Наприклад:

6 = 1+2 + 3; 28 =1 + 2 + 4+7 + 14.

Теорема Піфагора - фундаментальне співвідношення евклідової гео­метрії, яке в XIX ст. було взято за аналог метрик неевклідових гео­метрій.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 2

 

Теорема Піфагора

(доведення з використанням означення косинуса)

 

 

                                      С

 

 

 

 

 

 

 

 

 

А                                                                                                  B

 

                                                    D

За означенням косинуса кута  .

Звідки .

Аналогічно .

Звідки .

Додавши отримані рівності, маємо (пропонується закінчити доведення слухачам)

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 3

Доведення теореми Піфагора методом площ

 

 

1.              Розташуємо чотири рівних прямокутних трикутника так, як показано на малюнку.

 

 

 

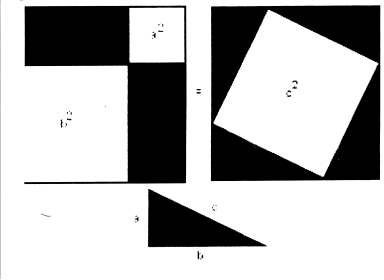
2.              Чотирикутник, який отримали, є квадратом, тому що сума двох гострих кутів 90 градусів, а розгорнутий кут – 180 градусів.

 

3.              Площа всієї фігури дорівнює, з одного боку, площі квадрата зі стороною (а+в), а з другого боку, сумі площ чотирьох трикутників та внутрішнього квадрату.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 4

 

Доведення Евкліда

 

 

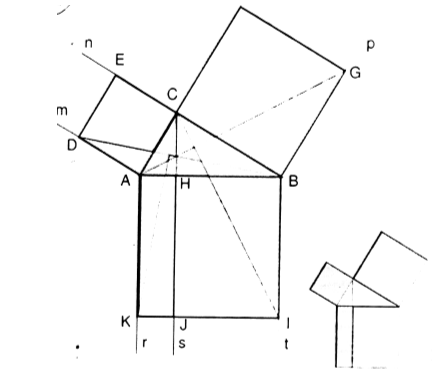
На сторонах прямокутного трикутника АВС побудовані квадрати АDEC,  BCFG та ABIK.

Проведемо промінь з вершини прямого кута С перпендикулярно гіпотенузі АВ, він поділить квадрат ABIK на два прямокутники. Площі цих прямокутників дорівнюють площам квадратів, побудованих на відповідних катетах (площа трикутника з тією ж висотою та основою, що і прямокутник, дорівнює половині площі заданого прямокутника).

Трикутник АСК дорівнює трикутнику BDA. (Чому?)

Аналогічно, .

Тим  самим, якщо позначити катети а и в, а гіпотенузу – с, то .

 

 

 

 

 

 

 

 

 

 

 

Додаток 5

 

Доведення Леонардо да Вінчі

 

 

 

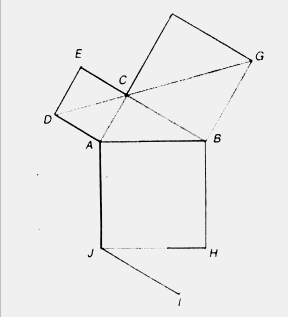
Головні елементи доведення – симетрія та рух.

Розглянемо уважно малюнок, як видно із симетрії, відрізок СІ ділить квадрат АВНJ на дві однакові частини (трикутники АВС та IHJ рівні за будовою). Виконавши поворот на 90 градусів проти часової стрілки, отримали рівні фігури CHJI та GDAB.

Площа заштрихованої частини дорівнює сумі половини площ квадратів, які побудовані на катетах та площі даного трикутника. Із другого боку, вона дорівнює половині площі квадрата, побудованого на гіпотенузі, плюс площа даного трикутника.

Зробіть висновки.