Позакласний захід з математики для учнів 11 класу за темою: "Чи можливо здати тест ЗНО з математики без калькулятора?"
Чи можливо здати тест ЗНО з математики без калькулятора?
Мета: Підвищити інтерес учнів до вивчення математики, ознайомити учнів з різноманітними
способами усної лічби, показати можливість застосування математичного апарату до
швидкого усного обчислення.
Розвивати уміння працювати у команді, стимулювати розумову та пізнавальну діяльність
учнів, логічне та критичне мислення.
Виховувати вміння вести дискусію, відстоювати свою точку зору.
Епіграф: «Числа керують світом», — казали піфагорійці. Це, звичайно, містика. Але числа дають змогу людині керувати світом, і в цьому нас переконує увесь хід розвитку науки й техніки наших днів»
- Діти, відповідно до теми заходу, які ваші очікування, чому ми сьогодні повинні навчитися,
які емоції повинні отримати? (хмаринка слів) https://wordart.com/dovwai18lnq8/%D0%B7%D0%BD%D0%BE
Нові знання, творча діяльність, співпраця в групах, отримати задоволення від власних успіхів, взаємодопомога, успішна робота, отримати гарний настрій.
Ви хочете добре здати ЗНО з математики? Тоді вам необхідно вміти рахувати швидко, правильно і без калькулятора. Адже головна причина втрати балів на ЗНО з математики - обчислювальні помилки. За правилами проведення тесту, користуватися калькулятором на іспиті забороняється. Ціна може бути занадто високою - видалення з екзамену. Насправді калькулятор на ЗНО з математики не потрібен. Всі завдання розв’язуються і без нього. Головне - увага, акуратність і деякі секретні прийоми, про які я вам розповім. А проведемо ми сьогоднішній урок цікавої математики у формі турніру, в якому будуть змагатися три команди: (представлення команд)
- Конкурс «Хто швидше?»
На початку нашої роботи проведемо невеличкий ескперимент - за який час ви обчислите значення цього виразу: 48 • 1,5 + 124 • 25 – 37 • 14 + ![]() ? Час пішов! (72 + 3100 – 518 +36 = 2690).
? Час пішов! (72 + 3100 – 518 +36 = 2690).
- 2) Конкурс «Розминка»
А тепер я нагадаю вам деякі прийоми, для швидкого та правильного обчислення без калькулятора, які ви вже знаєте.
1. Множення числа на 1,5.
Щоб помножити число на 1,5, треба до самого числа додати його половину. Наприклад,
24 · 1,5 = 24 + 12 = 36
(сам) 86 · 1,5 = 86+ 43= 129
2. Множення та ділення числа на 5.
Щоб число помножити на 5, потрібно помножити його на 10 і отриманий результат розділити на 2. Наприклад, 138 · 5 = (138 · 10) : 2 = 1380 : 2 = 690.
(сам) 247· 5 = (247 · 10) : 2 = 2470 : 2 =1235
Щоб число розділити на 5, потрібно помножити його на 2 і отриманий результат розділити на 10.
Наприклад, 71 : 5 = 71 · 2 : 10 =142 : 10 = 14,2.
(сам) 132 : 5 = 132· 2 : 10 = 264 : 10 = 26,4.
3. Множення числа на 25, на 125.
Щоб число помножити на 25, потрібно розділити його на 4 і результат помножити на 100.
Наприклад, 248 · 25 = 248 : 4 · 100 = 6200
(сам) 336 · 25 = 336 : 4 · 100 = 8400.
При множенні числа на 125 необхідно розділити його на 8 і результат помножити на 1000.
Наприклад, 248 · 125 = 248 : 8· 1000 = 31000.
(сам) 264 · 125 = 264 : 8· 1000 = 33000.
4. Пам’ятайте, що відповіді до завдань 21-29 ЗНО необхідно записувати лише десятковим дробом. Перевіряйте отриманий результат.
![]()
5. Активно використовуйте для обчислень формули скороченого множення.
Наприклад, як швидко і без стовпчика піднести до квадрату двозначне число? Застосовуємо формули скороченого множення: 192
![]() (сам) 532 = (50 + 3)2 = 2500 + 300 + 9 = 2809
(сам) 532 = (50 + 3)2 = 2500 + 300 + 9 = 2809
![]() (сам) 792 – 752 = (79 – 75)(79 + 75) = 4 · 154 = 616
(сам) 792 – 752 = (79 – 75)(79 + 75) = 4 · 154 = 616
А тепер, деякі секретні прийоми, для швидкого та правильного обчислення без калькулятора.
6. Піднесення до квадрата двозначних чисел, які закінчуються на 5, без калькулятора.
Існує алгоритм, який дозволяє дуже просто підносити до квадрата двозначні числа, які закінчуються на 5. Беремо будь-яке число, яке закінчується на п`ять, наприклад, А5. Множимо А на А + 1 і до отриманого результату дописуємо 25.
Наприклад, 752 = 5625, 7·8 = 56 та дописати 25. (сам) 952 = 9025, 9·10=90.
Взагалі алгоритм працює для будь-яких чисел, але тризначні числа підносити до квадрата складніше через те, що доводиться множити двозначні числа, які утворюються після відкидання п'ятірки.
Наприклад, 1252 = 15625, 12·13=156. (сам) 1352 = 18225
- 3) Конкурс «Незвичайні способи множення чисел»
7. Множення чисел в рядок.
Багато учнів не люблять множення в «стовпчик». Нікому не подобалося в п’ятому класі розв‘язувати нудні «приклади». Однак, множити числа в багатьох випадках можна і без «стовпчика», в рядок. Це набагато швидше:
![]()
![]() (сам)
(сам)
8. Множення чисел методом Ферроля.
Якщо не бажаєте множити в рядок, то можна скористатися способом, який отримав назву за прізвищем німецького інженера, який їм користувався – спосіб Ферроля.
Наприклад. 24 · 13 = (20 + 4)(10 + 3) = 200 + 60+40 + 12 = 312. Ось і результат!
(сам) 38 · 12 = (40 – 2)(10 + 2) = 400 + 80 – 20 – 4 = 456.
9. Італійський спосіб множення чисел.
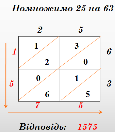
Розглянемо ще один цікавий графічний спосіб, що використовується в Італії. Цей метод був придуманий у Стародавній Індії видатним арабським математиком та астрономом Аль - Хорезми і був пізніше названий методом решітки. Щоб перемножити великі числа за його допомогою, потрібно накреслити сітку. По горизонталі зверху записуємо перший множник, а по вертикалі праворуч - другий. При цьому на кожну цифру повинна припадати одна клітина.
Тепер перемножимо цифри кожного ряду на цифри кожної колонки. Результат запишемо в клітку (розділену надвоє) на їх перетині. Якщо вийшло однозначне число, то в верхню частину клітини пишемо 0, а в нижню - отриманий результат. Залишилося скласти всі числа, які опинилися в діагональних смужках. Починаємо з нижньої правої клітки. Десятки при цьому додаємо до одиниць в сусідньому стовпчику. Наприклад, помножимо 25 на 63. (сам) 37·28 = 1036.
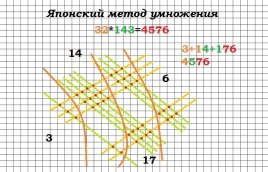
10. Японський спосіб множення чисел.
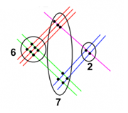
А цей графічний спосіб, яким користуються японські школярі, дозволяє легко перемножити дво і навіть тризначні числа. Розглянемо приклад 32·21.
На аркуші паперу по черзі малюємо лінії, кількість яких визначається за множниками прикладу.
Для множника 32 проводимо: 3 червоні лінії і трохи нижче – 2 сині. А для 21 перпендикулярно вже накресленим, проводимо спочатку 2 зелені, потім – 1 малинову. ВАЖЛИВО: лінії першого числа малюються в напрямку з верхнього лівого кута в нижній правий, другого числа – з нижнього лівого, у верхній правий. Потім рахуємо кількість точок перетину у кожній з трьох областей (на малюнку області позначені у вигляді кіл). Отже, в першій області (область сотень) – 6 точок, у другій (область десятків) – 7 точок, у третій (область одиниць) – 2 точки. Отже добуток 32·21 дорівнює 672.
 (сам) 24·32 = 768.
(сам) 24·32 = 768.
- 4) Конкурс «Дослідницький – цікаві результати»
Завдання першої команди:
1 х 1 = 1
11 х 11 = 121
111 х 111 = 12321
1111 х 1111 = 1234321
11111 х 11111 = 123454321
111111 х 111111 = 12345654321
1111111 х 1111111 = 1234567654321
11111111 х 11111111 = 123456787654321
111111111 х 111111111 = 12345678987654321
Завдання другої команди:
1 х 9 + 2 = 11
12 х 9 + 3 = 111
123 х 9 + 4 = 1111
1234 х 9 + 5 = 11111
12345 х 9 + 6 = 111111
123456 х 9 + 7 = 1111111
1234567 х 9 + 8 = 11111111
12345678 х 9 + 9 = 111111111
123456789 х 9 + 10 = 1111111111
Завдання третьої команди:
9 х 9 + 7 = 88
98 х 9 + 6 = 888
987 х 9 + 5 = 8888
9876 х 9 + 4 = 88888
98765 х 9 + 3 = 888888
987654 х 9 + 2 = 8888888
9876543 х 9 + 1 = 88888888
98765432 х 9 + 0 = 888888888
Сторінка відпочинку
Деякі зорові ілюзії пов'язані з тим, як працюють очі, але багато з них пов'язані з тим, як мозок обробляє сигнали, що надходять до нього.
1. Якщо дивитися на цю картинку уважно, вам буде здаватися, що листя рухаються один відносно іншого.

2. Якщо уважно дивитися на ці нерухомі диски, вам здасться, що вони обертаються. Зазвичай, якщо сконцентруватися у центрі одного з дисків, то цей уявний рух припиняється. Коли очі сканують картинку, переміщуючись по ній і намагаючись сфокусуватися на дрібних деталях, це викликає ефект «руху».

3. Мозок дивним чином вміє знаходити шаблони і заповнювати порожні місця у неповних даних. У тому числі він здатний сприймати такі «неможливі» картинки. Дуже складно відокремити ноги слона від фону картинки.

4.Скільки кольорів використано на гранях куба? Якщо ви нарахували сім (білий, жовтий, синій, червоний, зелений, коричневий і помаранчевий), то ви не тільки знайшли найпопулярнішу відповідь, але ще й помилилися, як більшість людей. Насправді там всього шість кольорів. Центральна плашка верхньої грані (яка виглядає коричневою) має той самий колір, що і центральна плашка передньої грані (яка виглядає помаранчевою). У це неможливо повірити, а перевірити можна, лише використовуючи папірець з двома отворами або за допомогою фото шопа.

5. Бачите куб? А його там немає. Іноді мозок в спробах знайти знайомі форми і надати зображенню смисл заходить занадто далеко. Він додає ребра там, де немає ні зміни кольору, ні зміни текстури.

- 5) Конкурс «Обчислення квадратного кореня з числа без калькулятора»
11. Обчислення квадратного кореня з числа без калькулятора.
А як взагалі обчислити квадратний корінь з числа без калькулятора? Розглянемо два способи.
а) Перший спосіб - розкладання підкореневого виразу на множники. Наприклад, обчислимо![]() . Число 6561 ділиться на 3 (так як сума його цифр ділиться на 3). Розкладемо 6561 на множники:
. Число 6561 ділиться на 3 (так як сума його цифр ділиться на 3). Розкладемо 6561 на множники:
6561 = 9 · 9 · 81 = 81 · 81
![]()
(сам) Знайдемо ![]() . Це число ділиться на 2. На 3 воно теж ділиться. Розкладаємо 2916 на множники.
. Це число ділиться на 2. На 3 воно теж ділиться. Розкладаємо 2916 на множники.
![]()
б) Другий спосіб - наприклад, треба обчислити![]() . Число під коренем - непарне, воно не ділиться на 3, не ділиться на 5, не ділиться на 7 ... Можна і далі шукати, на що ж воно все-таки ділиться, а можна зробити простіше - знайти цей корінь підбором.
. Число під коренем - непарне, воно не ділиться на 3, не ділиться на 5, не ділиться на 7 ... Можна і далі шукати, на що ж воно все-таки ділиться, а можна зробити простіше - знайти цей корінь підбором.
702 = 4900, 802 = 6400, а число 5041 знаходиться між ними. Першу цифру у відповіді ми вже знаємо, це 7. Остання цифра в числі 5041 дорівнює 1. Оскільки 12 = 1, а 92 = 81, остання цифра у відповіді - або 1, або 9. Перевіримо:
712 = (70 + 1)2 = 4900 + 140 + 1 = 5041.
(сам) Обчислимо ![]() . 502 = 2500, 602 = 3600. Значить, перша цифра у відповіді - п'ятірка.
. 502 = 2500, 602 = 3600. Значить, перша цифра у відповіді - п'ятірка.
У числі 2809 остання цифра - дев'ятка. 32 = 9, 72 = 49.
Це означає, що остання цифра у відповіді - або 3, або 9. Перевіримо:
![]()
- 6) Конкурс «Підсумковий»
А тепер проведемо той самий ескперимент, тільки в кінці нашої роботи - за який час ви обчислите значення цього виразу: 64 • 1,5 + 652 – 46 • 21 + ![]() ? Час пішов! (96 + 4225 – 966 + 48 = 3403)
? Час пішов! (96 + 4225 – 966 + 48 = 3403)
Підведення підсумків.
Сайт математика без калькулятора
Реклама
Реклама амбіцій:
Амбіції - це коли ідеш на ЗНО з математики, думаючи, що знаєш на 2 бали, а коли отримуєш там 8 балів, то обурюєшся, чому не 10.
Гімназисти жартують
1. Лекція з математики - це процес переходу записів учителя в зошит учня без проходу через чийсь мозок.
2. Учитель, звертаючись до учня:
- Шановний, чому ти спиш на уроці?
- Я не сплю, я повільно моргаю.
3. Вчителі приймали іспит з математики та валеріанку. Здавали учні та нерви.
4. Вчитель, опитуючи учня, щоб поставити йому бодай хоч яку-небудь оцінку, запитує:
- Ну добре. Скажи, на яку тему було задано домашнє завдання?
Учень мовчить.
- Так ... Скажи хоч, хто вів урок. Учень мовчить.
- Пряме питання: ти чи я?
5. Гімназист, що вступив до 5 класу: Ну, все, виженуть. Точно виженуть ...
Гімназист, що перейшов до 6 класу: А може, не виженуть?
Гімназист, що перейшов до 7 класу: Та ні, таки виженуть.
Гімназист, що перейшов до 8 класу: Ну, тепер не виженуть ...
Гімназист, що перейшов до 9 класу: Треба добре здати ДПА, а то не візьмуть до 10 класу.
Гімназист, що вступив до 10 класу: Ну, точно, тепер не виженуть.
Гімназист, що перейшов до 11 класу: Таки ж не виженуть... Хай тільки спробують!
6. Учитель учню: - Ти знову не підготувався? Адже обіцяв стати в цьому семестрі іншою людиною ...
Учень: - А я і став іншою людиною, але віна теж виявилася ледарем.
Наш практикум
А зараз вас чекає зустріч з нашими практиками, які ознайомлять вас з цікавим обчисленням на сторінці «Наш практикум».
1. Обчислення квадратного кореня з будь-якого числа без калькулятора.
Нехай потрібно обчислити квадратний корінь з натурального числа m, причому відомо, що корінь з даного числа добувається. Щоб знайти результат, іноді зручно скористатися таким правилом:
1. Розіб'ємо число m на грані (справа наліво, починаючи з останньої цифри), включивши в кожну грань по дві цифри, що стоять поруч. При цьому слід врахувати, що, якщо m складається з парного числа цифр, то в першій (зліва) грані буде дві цифри; якщо ж число m складається з непарного числа цифр, то перша грань складається з однієї цифри. Кількість граней показує кількість цифр, отриманих у результаті добування кореня з числа m.
2. Підбираємо найбільшу цифру так, щоб її квадрат не перевищував би числа, яке знаходиться в першій грані; ця цифра є першою цифрою результату.
3. Піднесемо першу цифру результату до квадрата та віднімемо отримане число від числа першої грані, до знайденої різниці припишемо праворуч другу грань. Вийде деяке число A. Подвоївши отриману цифру результату, отримаємо число а. Тепер підберемо таку найбільшу цифру x, щоб добуток числа ![]() на x не перевищував би числа А. Цифра x - друга цифра результату.
на x не перевищував би числа А. Цифра x - друга цифра результату.
4. Добуток числа ![]() на x віднімемо від числа A та припишемо до знайденої різниці праворуч третю грань, вийде деяке число B. Подвоївши отримане число в результаті, отримаємо число b. Тепер підберемо таку найбільшу цифру y, щоб добуток числа
на x віднімемо від числа A та припишемо до знайденої різниці праворуч третю грань, вийде деяке число B. Подвоївши отримане число в результаті, отримаємо число b. Тепер підберемо таку найбільшу цифру y, щоб добуток числа ![]() на y не перевищував би числа B. Цифра y - третя цифра результату.
на y не перевищував би числа B. Цифра y - третя цифра результату.
Наступний крок правила повторює 4 -й крок. Так продовжуємо до тих пір, поки не використаємо останню грань числа.
Наприклад: обчислити![]()
Розв’язання. Розіб'ємо число на грані: 13'83'84 - їх три, отже, в результаті отримаємо тризначне число. Перша цифра результату 3, так як 32 < 13, тоді як 42 > 13. Віднявши 9 із 13, отримаємо 4. Приписавши до 4 наступну грань, отримаємо A = 483. Подвоївши отриману цифру результату, тобто, число 3, отримаємо a = 6. Тепер підберемо таку найбільшу цифру x, щоб добуток двозначного числа ![]() на x був би менше за число 483. Такою цифрою буде 7, так як 67 * 7 = 469 - це менше за 483, тоді як 68 * 8 = 544 - це більше за 483. Отже, друга цифра результату 7. Віднявши 469 із 483, отримаємо 14. Приписавши до цього числа праворуч останню грань, отримаємо b = 1484. Подвоївши отримане число в результаті, тобто число 37, отримаємо B = 74. Підберемо тепер таку найбільшу цифру y, щоб добуток тризначного числа
на x був би менше за число 483. Такою цифрою буде 7, так як 67 * 7 = 469 - це менше за 483, тоді як 68 * 8 = 544 - це більше за 483. Отже, друга цифра результату 7. Віднявши 469 із 483, отримаємо 14. Приписавши до цього числа праворуч останню грань, отримаємо b = 1484. Подвоївши отримане число в результаті, тобто число 37, отримаємо B = 74. Підберемо тепер таку найбільшу цифру y, щоб добуток тризначного числа ![]() на y не перевищував би 1484. Такою цифрою буде 2, так як 742 * 2 = 1484. Цифра 2 - остання цифра результату. У відповіді отримали - 372.
на y не перевищував би 1484. Такою цифрою буде 2, так як 742 * 2 = 1484. Цифра 2 - остання цифра результату. У відповіді отримали - 372.
Отже, ![]()
8. Множення чисел на пальцях.
Якщо не бажаєте записувати свої дії у рядок, то можна виконувати множення на пальцях.
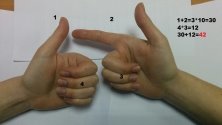
Цей метод дозволяє множити числа від 6 до 9. Для початку зігніть обидві руки в кулаки. Потім на лівій руці відігніть стільки пальців, на скільки перший множник більше за число 5. На правій руці виконайте ті самі дії тільки для другого множника. Порахуйте кількість розігнутих пальців і помножте суму на десять. А тепер перемножте суму загнутих пальців лівої і правої руки. Склавши обидві суми, отримаємо результат.
Наприклад. Помножимо 6 на 7. Шість більше п'яти на один, отже на лівій руці відгинаємо один палець. А сім - на два, значить на правій - два пальця. У сумі - це три, а після множення на 10 - 30. Тепер перемножимо чотири загнутих пальці лівої руки і три - правої. Отримаємо 12. Сума 30 і 12 дасть 42.
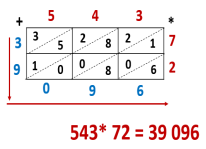
Наприклад. Помножимо 32 на 143. Для цього намалюємо сітку: перше число зобразимо трьома і двома лініями з відступом по горизонталі, а друге - однією, чотирма і трьома лініями по вертикалі. У місцях перетину ліній поставимо точки. В результаті у нас повинно вийти чотиризначне число, тому умовно розділимо таблицю на 4 сектори. І перерахуємо точки, що потрапили в кожний з них. Отримаємо 3, 14, 17 і 6. Щоб отримати відповідь, зайві одинички у 14 і 17 додамо до попереднього числа. Отримаємо 4, 5 і 76 - 4576.
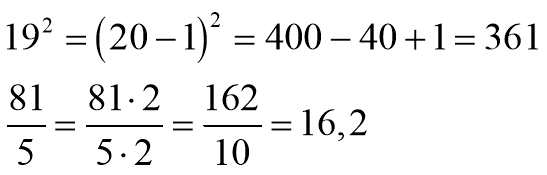
1


про публікацію авторської розробки
Додати розробку
