Збірник "Задачі з практичним змістом"

Збірник задач з практичним змістом для учнів 10- 11кл. ВідсоткиІнтеграл та його застосування. Теорія імовірностей. Площі та об’єми многогранників та тіл обертання

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 1. Від продажу продукції на 1500 гривень власник пекарні отримав 20% прибутку. Знайти собівартість товару. Розв’язування: Показати. Собівартість продукції приймаємо за 100%. Вартість продукції 1500 гривень при продажі становить 100%. +20% собівартості. Тоді собівартість дорівнює:1500120×100%=1250(гривень)Відповідь: собівартість дорівнює1250(гривень)Примітка. В процесі розв'язання варто розкрити учням зміст поняття «собівартість» товару. 

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 2. Скільки котлетного м’яса можна отримати при тушінні яловичини першої категорії угодованості масою 150 кг., якщо норма виходу котлетного м’яса до маси м’яса на кістках складає 40,3%Розв’язування: Показати. Складаємо пропорцію:150кг. —100% Хкг. —40,3% Х=150кг. ×40,3100%=60,45кг. Відповідь: 60,45кг. 

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 3. Власник кафе у жовтні витратив 150 квт електроенергії, а в листопаді на 20% більше. Якщо 1 квт коштує 0,36 грн., то на скільки відсотків більше заплатив власник кафе у листопаді, ніж у жовтні?Розв’язування: Показати. Складаємо пропорцію:150квт. —100%Хквт. —20%Х= 150квт.×20%100%=30квт.150квт.+30квт.=180квт.150квт.×0,36=54грн.180квт.×0,36=64,8грн.54грн. —100%64,8грн. —Х%Х=120%Відповідь: 20% 

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 4. Власник пекарні отримав кредит на суму 20000 грн під 32 % річних. Через 240 днів кредит було повністю погашено. Розрахуйте, яку суму власник пекарні віддав банку? На скільки різниться ця сума від позиченої?Розв’язування: Показати. Розв'язання: Застосовуємо формулу простих відсотків для обчислень𝑃𝑖=𝑃×1+𝑛100%×𝑑365𝑃𝑖=20000×1+32100×240365=24208,22(грн)Відповідь: 4208,22грн. 

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 5. Експрес обід в ресторані коштує 200 грн. Спочатку його ціну підвищили на кілька відсотків, а потім знизили на стільки ж відсотків, після чого вартість його стала 192 грн. На скільки відсотків кожного разу відбувалася зміна ціни обіду? Розв’язування: Показати. Розв'язання: Оскільки відсотки однакові, то позначаємо зміну ціни товару через X. Н а основі умови задачі отримаємо рівняння2001+Х1−Х=192 Його спрощення приведе до розв'язування рівняння 8−200 Х2=0 звідки корені набудуть значень Х=−0,2;Х=0,2 Перше значення відкидаємо, воно міняє суть задачі (спочатку маємо зниження, а потім ріст відсотків, що суперечить умові). Друге при перерахунку становитиме 0,2*100% = 20% відсотків. Відповідь: 20% 

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 6. Блендер коштував 600 гривень. Спочатку його ціну зменшили на 20%, а згодом підвищили на 25%. Як змінилась ціна блендера?Розв’язування: Показати. Розв'язання: Зменшена ціна становить 100-20=80% або 0,8. Таким чином нова ціна рівна 0,8*600=480 грн. Після підвищення на 25 процентів нова ціна становила 125% від 480, тобто 1,25*480=600 грн. Відповідь: Ціна повернулась до початкового значення

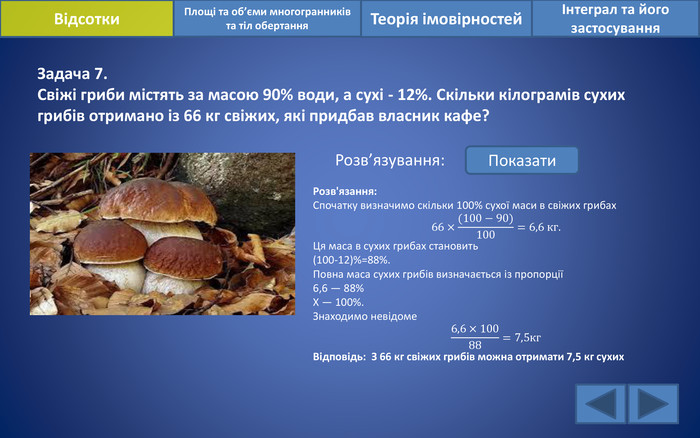
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 7. Свіжі гриби містять за масою 90% води, а сухі - 12%. Скільки кілограмів сухих грибів отримано із 66 кг свіжих, які придбав власник кафе?Розв’язування: Показати. Розв'язання: Спочатку визначимо скільки 100% сухої маси в свіжих грибах66×(100−90)100=6,6 кг. Ця маса в сухих грибах становить (100-12)%=88%. Повна маса сухих грибів визначається із пропорції6,6 — 88%Х — 100%. Знаходимо невідоме6,6×10088=7,5кг. Відповідь: З 66 кг свіжих грибів можна отримати 7,5 кг сухих 

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 1. Скільки повних порцій супу міститься у каструлі .яка має форму циліндра, висота якого 30 см.,а діаметр 20см. Відомо. що одна порція містить 0.25л. супу. Розв’язування: Показати. Дано: V= 0,25л. = 250смᶾh = 30см. R = 10см. Знайти n кількість порцій. Розв’язування: V =πR²h = 3,14×10²×30 =9420(смᶾ)𝑛=9420250=37,68≈38(порцій)Відповідь: ≈38 (порцій) 

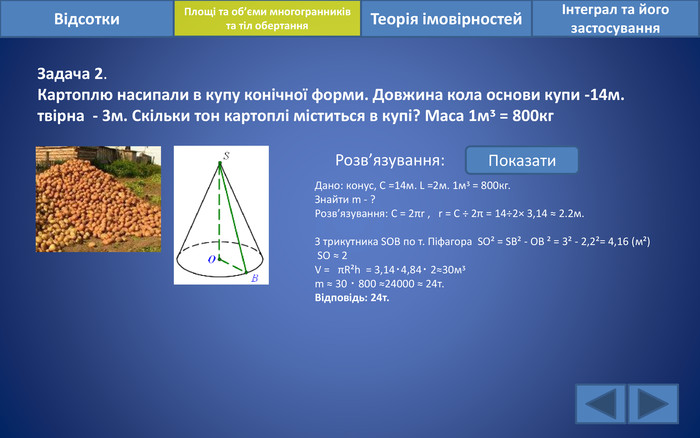
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 2. Картоплю насипали в купу конічної форми. Довжина кола основи купи -14м. твірна - 3м. Скільки тон картоплі міститься в купі? Маса 1мᶾ = 800кг. Розв’язування: Показати. Дано: конус, С =14м. L =2м. 1мᶾ = 800кг. Знайти m - ? Розв’язування: C = 2πr , r = С ÷ 2π = 14÷2× 3,14 ≈ 2.2м. З трикутника SOB по т. Піфагора SO² = SB² - OB ² = 3² - 2,2²= 4,16 (м²) SO ≈ 2 V = πR²h = 3,14‧4,84‧ 2≈30мᶾm ≈ 30 ‧ 800 ≈24000 ≈ 24т. Відповідь: 24т.

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 3. Цукор-рафінад виготовляють у вигляді шматочків, що мають форму прямокутного паралелепіпеда розмірами 24 мм х 2 4м м х 10 мм. Скільки шматочків цукру повинно міститися у пачці масою 0,5 кг? Питома вага цукру 1,2 г.\смᶾРозв’язування: Показати. Об’єм прямокутного паралелепіпеда дорівнює: V= а‧в‧с = 24 мм ‧ 2 4м м ‧ 10 мм.= 5,760 см³Маса одного брусочка цукру дорівнює 1,2 ‧5,760 = 6,912г.0,5кг= 500г, отже: 500 : 6,912≈71 Відповідь: ≈71 штук

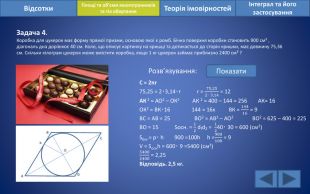
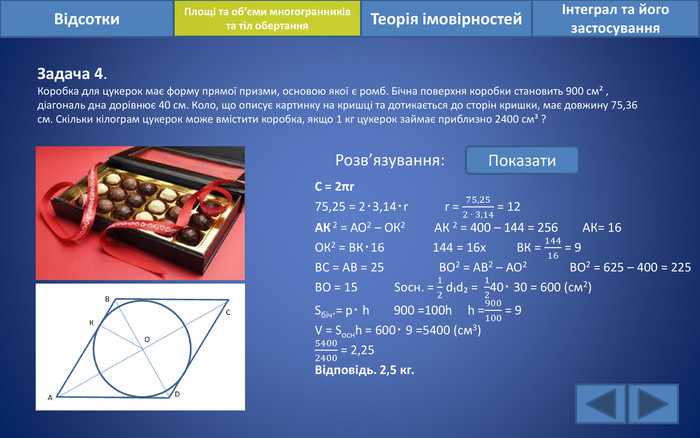
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 4. Коробка для цукерок має форму прямої призми, основою якої є ромб. Бічна поверхня коробки становить 900 см² , діагональ дна дорівнює 40 см. Коло, що описує картинку на кришці та дотикається до сторін кришки, має довжину 75,36 см. Скільки кілограм цукерок може вмістити коробка, якщо 1 кг цукерок займає приблизно 2400 см³ ?Розв’язування: Показати. С = 2πr75,25 = 2‧3,14‧r r = 75,252 ‧ 3,14 = 12 АК 2 = АО2 – ОК2 АК 2 = 400 – 144 = 256 АК= 16 ОК2 = ВК‧16 144 = 16х ВК = 14416 = 9 ВС = АВ = 25 ВО2 = АВ2 – АО2 ВО2 = 625 – 400 = 225 ВО = 15 Sосн. = 12 d₁d₂ =  1240‧ 30 = 600 (см2)Sбіч.= р‧ h 900 =100h h =900100 = 9 V = Sоснh = 600‧ 9 =5400 (см3)54002400 = 2,25 Відповідь. 2,5 кг. 

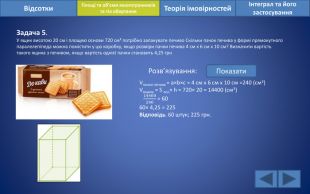
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 5. У ящик висотою 20 см і площею основи 720 см² потрібно запакувати печиво Скільки пачок печива у формі прямокутного паралелепіпеда можна помістити у цю коробку, якщо розміри пачки печива 4 см х 6 см х 10 см? Визначити вартість такого ящика з печивом, якщо вартість однієї пачки становить 4,25 грн Розв’язування: Показати. Vпачки печива = a×b×c = 4 см х 6 см х 10 см =240 (cм3)Vящика = S осн× h = 720× 20 = 14400 (cм3) 14400240 = 6060× 4,25 = 225 Відповідь. 60 штук; 225 грн. 

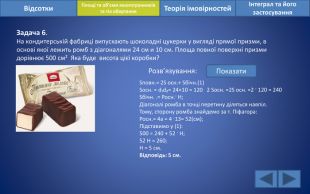
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 6. На кондитерській фабриці випускають шоколадні цукерки у вигляді прямої призми, в основі якої лежить ромб з діагоналями 24 см и 10 см. Площа повної поверхні призми дорівнює 500 см² Яка буде висота цієї коробки? Розв’язування: Показати. Sповн.= 2 S осн.+ Sбічн.(1) Sосн. = d₁d₂= 24×10 = 120 2 Sосн. =2 S осн. =2 · 120 = 240 Sбічн. .= Росн.· H;Діагоналі ромба в точці перетину діляться навпіл. Тому, сторону ромба знайдемо за т. Піфагора: Росн.= 4а = 4 ·13= 52(см);Підставимо у (1):500 = 240 + 52 · H;52 H = 260;H = 5 см. Відповідь: 5 см.

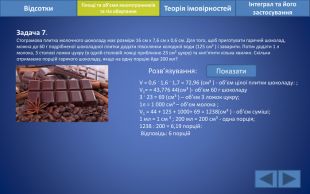
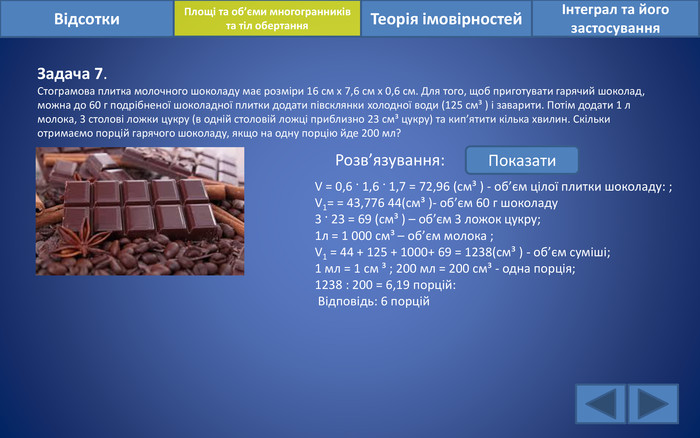
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 7. Стограмова плитка молочного шоколаду має розміри 16 см х 7,6 см х 0,6 см. Для того, щоб приготувати гарячий шоколад, можна до 60 г подрібненої шоколадної плитки додати півсклянки холодної води (125 см³ ) і заварити. Потім додати 1 л молока, 3 столові ложки цукру (в одній столовій ложці приблизно 23 см³ цукру) та кип’ятити кілька хвилин. Скільки отримаємо порцій гарячого шоколаду, якщо на одну порцію йде 200 мл? Розв’язування: Показати. V = 0,6 · 1,6 · 1,7 = 72,96 (см³ ) - об’єм цілої плитки шоколаду: ;V1= = 43,776 44(см³ )- об’єм 60 г шоколаду3 · 23 = 69 (см³ ) – об’єм 3 ложок цукру;1л = 1 000 см³ – об’єм молока ;V1 = 44 + 125 + 1000+ 69 = 1238(см³ ) - об’єм суміші; 1 мл = 1 см ³ ; 200 мл = 200 см³ - одна порція; 1238 : 200 = 6,19 порцій: Відповідь: 6 порцій

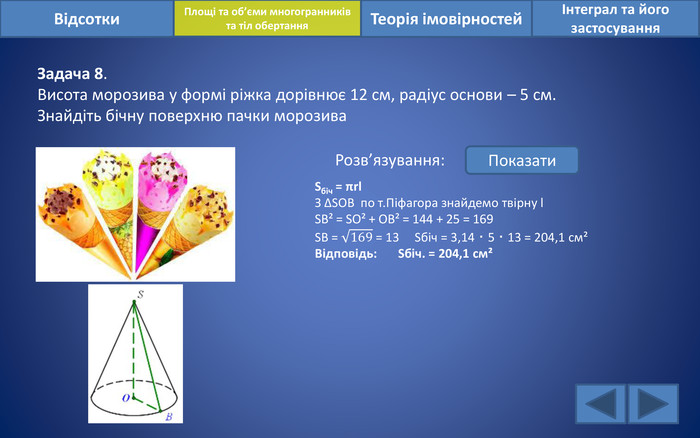
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 8. Висота морозива у формі ріжка дорівнює 12 см, радіус основи – 5 см. Знайдіть бічну поверхню пачки морозива Розв’язування: Показати. Sбіч = πrl. З ∆SOB по т. Піфагора знайдемо твірну l SB² = SO² + OB² = 144 + 25 = 169 SB = 169 = 13 Sбіч = 3,14 ‧ 5 ‧ 13 = 204,1 см²Відповідь: Sбіч. = 204,1 см² 

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 9. Соковитискач має циліндричну форму. У скільки разів збільшиться площа його бічної поверхні, якщо радіус його основи збільшити у 4 рази, а висоту у 2 рази. Розв’язування: Показати. Sбіч.= 2πRHSбіч1= 2π‧4 R‧2 H = 16 πRH; 𝟏𝟔 𝝅𝑹𝑯𝟐𝝅𝑹𝑯 = 8 Відповідь: 8 раз 

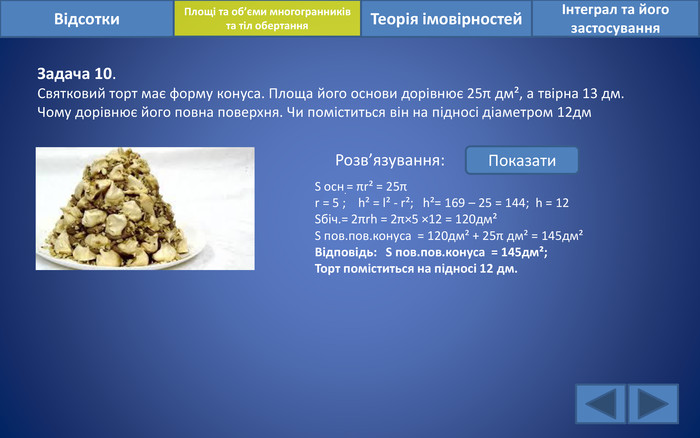
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 10. Святковий торт має форму конуса. Площа його основи дорівнює 25π дм², а твірна 13 дм. Чому дорівнює його повна поверхня. Чи поміститься він на підносі діаметром 12дм. Розв’язування: Показати. S осн.= πr² = 25πr = 5 ; h² = l² - r²; h²= 169 – 25 = 144; h = 12 Sбіч.= 2πrh = 2π×5 ×12 = 120дм²S пов.пов.конуса = 120дм² + 25π дм² = 145дм² Відповідь: S пов.пов.конуса = 145дм²; Торт поміститься на підносі 12 дм.

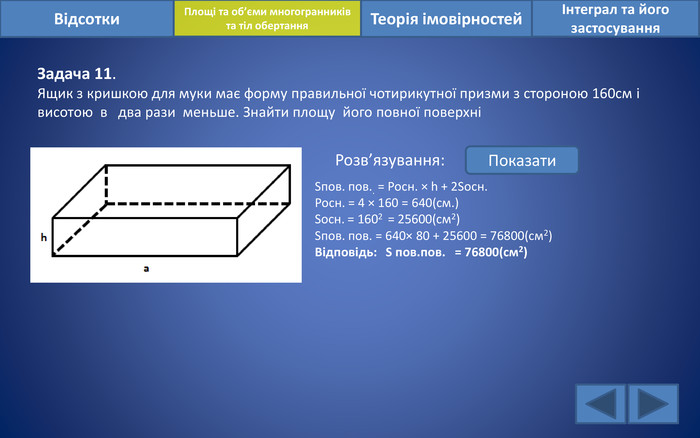
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 11. Ящик з кришкою для муки має форму правильної чотирикутної призми з стороною 160см і висотою в два рази меньше. Знайти площу його повної поверхніРозв’язування: Показати. Sпов. пов.. = Росн. × h + 2 Sосн. Росн. = 4 × 160 = 640(см.)Sосн. = 1602 = 25600(см2)Sпов. пов. = 640× 80 + 25600 = 76800(см2)Відповідь: S пов.пов. = 76800(см2)

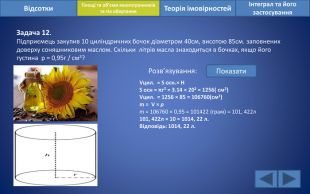
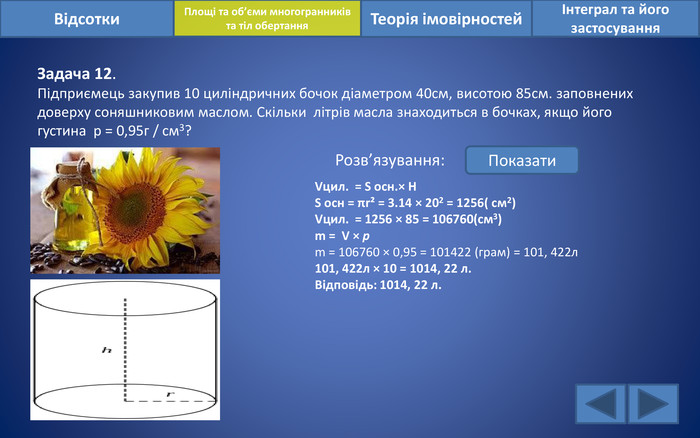
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 12. Підприємець закупив 10 циліндричних бочок діаметром 40см, висотою 85см. заповнених доверху соняшниковим маслом. Скільки літрів масла знаходиться в бочках, якщо його густина р = 0,95г / см3?Розв’язування: Показати. Vцил. = S осн.× H S осн = πr² = 3.14 × 202 = 1256( см2)Vцил. = 1256 × 85 = 106760(см3)m = V × рm = 106760 × 0,95 = 101422 (грам) = 101, 422л101, 422л × 10 = 1014, 22 л. Відповідь: 1014, 22 л.

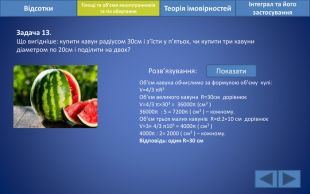
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 13. Що вигідніше: купити кавун радіусом 30см і з’їсти у п’ятьох, чи купити три кавуни діаметром по 20см і поділити на двох?Розв’язування: Показати. Об’єм кавуна обчислимо за формулою об’єму кулі: V=4/3 πR3 Об’єм великого кавуна R=30см дорівнюєV=4/3 π×303 = 36000π (см3 )36000π : 5 = 7200π ( см3 ) – кожному. Об’єм трьох малих кавунів R=d:2=10 см дорівнюєV=3× 4/3 π103 = 4000π ( см3 )4000π : 2= 2000 ( см3 ) – кожному. Відповідь: один R=30 см

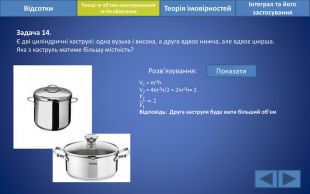
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 14. Є дві циліндричні каструлі: одна вузька і висока, а друга вдвоє нижча, але вдвоє ширша. Яка з каструль матиме більшу місткість?Розв’язування: Показати. V1 = πr2h. V2 = 4πr2h/2 = 2πr2h= 2𝑉2𝑉1=2 Відповідь: Друга каструля буде мати більший об’єм 

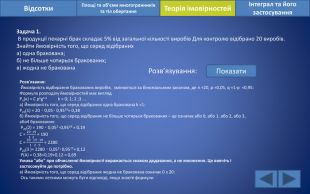
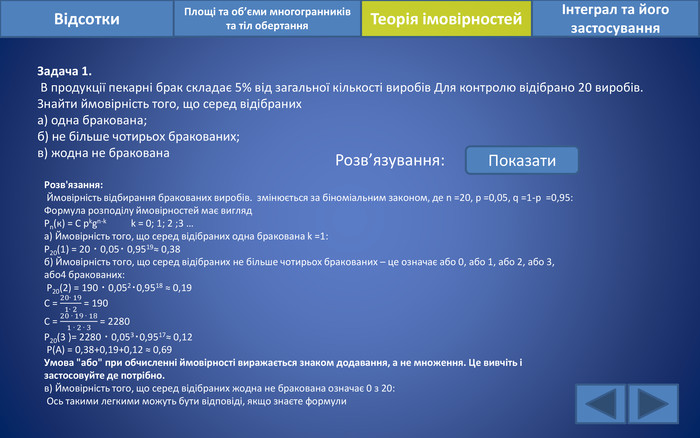
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 1. В продукції пекарні брак складає 5% від загальної кількості виробів Для контролю відібрано 20 виробів. Знайти ймовірність того, що серед відібраниха) одна бракована;б) не більше чотирьох бракованих;в) жодна не бракована. Розв’язування: Показати. Розв'язання: Ймовірність відбирання бракованих виробів. змінюється за біноміальним законом, де n =20, p =0,05, q =1-p =0,95: Формула розподілу ймовірностей має вигляд. Рn(к) = C pkgn-k k = 0; 1; 2 ;3 …а) Ймовірність того, що серед відібраних одна бракована k =1: Р20(1) = 20 ‧ 0,05‧ 0,9519≈ 0,38б) Ймовірність того, що серед відібраних не більше чотирьох бракованих – це означає або 0, або 1, або 2, або 3, або4 бракованих: Р20(2) = 190 ‧ 0,052‧0,9518 ≈ 0,19 С = 20‧ 191‧ 2 = 190 С = 20 ‧ 19 ‧ 181 ‧ 2 ‧ 3 = 2280 Р20(3 )= 2280 ‧ 0,053‧0,9517≈ 0,12 Р(А) = 0,38+0,19+0,12 ≈ 0,69 Умова "або" при обчисленні ймовірності виражається знаком додавання, а не множення. Це вивчіть і застосовуйте де потрібно.в) Ймовірність того, що серед відібраних жодна не бракована означає 0 з 20:  Ось такими легкими можуть бути відповіді, якщо знаєте формули 

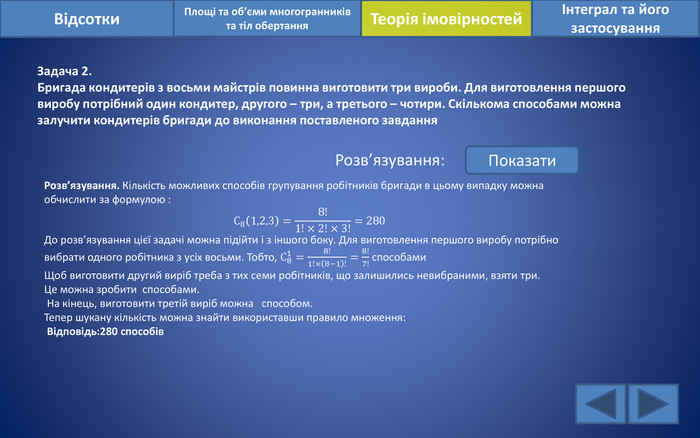
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 2. Бригада кондитерів з восьми майстрів повинна виготовити три вироби. Для виготовлення першого виробу потрібний один кондитер, другого – три, а третього – чотири. Скількома способами можна залучити кондитерів бригади до виконання поставленого завдання. Розв’язування: Показати. Розв’язування. Кількість можливих способів групування робітників бригади в цьому випадку можна обчислити за формулою : С81,2,3=8!1!×2!×3!=280 До розв’язування цієї задачі можна підійти і з іншого боку. Для виготовлення першого виробу потрібно вибрати одного робітника з усіх восьми. Тобто, С81=8!1!×8−1!=8!7! способами. Щоб виготовити другий виріб треба з тих семи робітників, що залишились невибраними, взяти три. Це можна зробити способами. На кінець, виготовити третій виріб можна способом. Тепер шукану кількість можна знайти використавши правило множення: Відповідь:280 способів 

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 3.Із шести офіціантів і трьох поварів треба сформувати бригаду із 5 осіб, у яку входив би хоча б один повар. Скількома способами це можна зробити?Розв’язування: Показати. У сформованій бригаді може бути один, два чи три повара. Із наявнихтрьох поварів їх можна вибрати, С31, С32, С33 відповідно способами. Тодісеред 5 осіб бригади буде, відповідно, чотири, три чи два офіціанта. Для знаходження кінцевого результату необхідно використати в комбінації правило множення і додавання. Тому шукана кількість будерозраховуватися за такою формулою: С𝟑𝟏×С𝟔𝟒+С𝟑𝟐×С𝟔𝟑+С𝟑𝟑×С𝟔𝟐==𝟑!𝟏!×𝟐!×𝟔!𝟒!×𝟐!+𝟑!𝟐!×𝟏!×𝟔!𝟑!×𝟑!+𝟑!𝟑!×𝟎!×𝟔!𝟐!×𝟒!=𝟑×𝟓×𝟔𝟐+𝟑×𝟓+𝟏×𝟓×𝟔𝟐=𝟕𝟓 Відповідь: 75 способів 

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 4. До складу фруктового салата входять: 1 апельсин, 1 груша, 1 яблоко. Скількома способами повар може вибрати інградієнти для салату, якщо у нього є 10 яблук, 11 груш и 8 апельсинів. Розв’язування: Показати. Так як до складу салату входять всі інгредієнти то використовуємоправило добутку: 10 × 11× 8 = 880 Відповідь: 880 способів

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 5. В учнівській їдальні є 4 перших, 5 других и 6 третіх блюд. Скількома способами можна вибрати обід з трьох блюд, щоб було перше, друге і третє блюдо?Розв’язування: Показати. Щоб не перераховувати всі можливі варіанти, міркуємо так: 1 з 4 першихблюд можемо обрати 4 варіантами, 2 з 5 других блюд можемо обрати 5 варіантами і 3 з 6 третіх блюд можемо обрати 6 варіантами. Отже ,за правилом добутку всього існує 4 × 5 × 6 = 120 Відповідь: 120 способів

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 6. З 25 учнів групи «Кухар кондитер» потрібно вибрати 5, для уучасті в конкурсі кулінарної майстерності. В групі навчається 18 дівчат , 7 хлопців. Скількома способами можна вибрати на конкурс 3-х дівчат і 2-х хлопців?Розв’язування: Показати. З умови завдання випливає, що порядок вибору учнів не важливий, тому з 18 дівчат можна вибрати С183 = 18 ×17× 161 × 2 × 3  = 816 способами, а хлопців С72 = 7× 61× 2 = 21 спосіб. Добуток цих комбінацій дасть нам відповідь.816×21 =17 136 Відповідь: 17 136 способів 

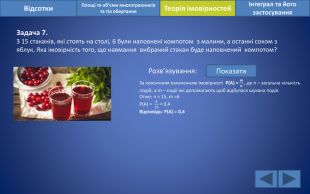
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 7. З 15 стаканів, які стоять на столі, 6 були наповнені компотом з малини, а останні соком з яблук. Яка імовірність того, що навмання вибраний стакан буде наповнений компотом?Розв’язування: Показати. За класичним означенням імовірності Р(А) = 𝒎𝒏 , де n – загальна кількість подій, а m – події які допомагають щоб відбулася шукана подія. Отже: n = 15, m =6 Р(А) =  615 = 0,4 Відповідь: Р(А) = 0,4 

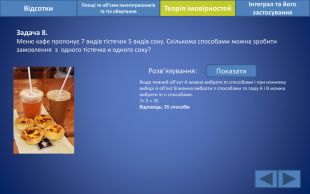
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 8. Меню кафе пропонує 7 видів тістечок 5 видів соку. Скількома способами можна зробити замовлення з одного тістечка и одного соку?Розв’язування: Показати. Якщо певний об’єкт А можна вибрати m способами і при кожному виборі А об’єкт В можна вибрати n способами то пару А і В можна вибрати m n способами.7× 5 = 35 Відповідь: 35 способів

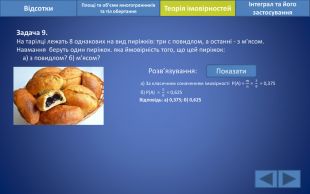
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 9. На тарілці лежать 8 однакових на вид пиріжків: три с повидлом, а останні - з м’ясом. Навмання беруть один пиріжок. яка ймовірність того, що цей пиріжок: а) з повидлом? б) м’ясом?Розв’язування: Показати а) За класичним означенням імовірності Р(А) = 𝑚𝑛 =  38 = 0,375 б) Р(А) = 58  = 0,625 Відповідь: а) 0,375; б) 0,625 

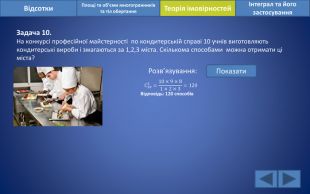
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 10. На конкурсі професійної майстерності по кондитерській справі 10 учнів виготовляють кондитерські вироби і змагаються за 1,2,3 міста. Скількома способами можна отримати ці міста?Розв’язування: Показати. С103=10×9×81×2×3=120 Відповідь: 120 способів 

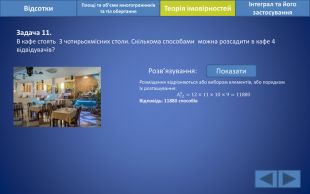
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 11. В кафе стоять 3 чотирьохмісних столи. Скількома способами можна розсадити в кафе 4 відвідувачів? Розв’язування: Показати. Розміщення відрізняються або вибором елементів, або порядком їх розташування: А124=12×11×10×9=11880 Відповідь: 11880 способів 

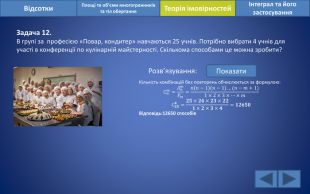
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 12. В групі за професією «Повар, кондитер» навчаються 25 учнів. Потрібно вибрати 4 учнів для участі в конференції по кулінарній майстерності. Скількома способами це можна зробити?Розв’язування: Показати. Кількість комбінацій без повторень обчислюється за формулою: С𝑛𝑚=𝐴𝑛𝑚𝑃𝑚=𝑛𝑛−1𝑛−1…(𝑛−𝑚+1)1×2×3×…×𝑚С𝟐𝟓𝟒=𝟐𝟓×𝟐𝟒×𝟐𝟑×𝟐𝟐𝟏×𝟐×𝟑×𝟒=𝟏𝟐𝟔𝟓𝟎 Відповідь:12650 способів 

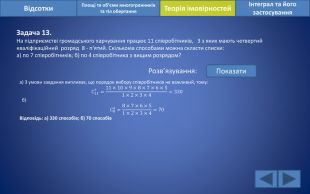
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 13. На підприємстві громадського харчування працює 11 співробітників, 3 з яких мають четвертий кваліфікаційний розряд 8 - п'ятий. Скількома способами можна скласти списки:а) по 7 співробітників; б) по 4 співробітника з вищим розрядом?Розв’язування: Показатиа) З умови завдання випливає, що порядок вибору співробітників не важливий, тому: С117=11×10×9×8×7×6×51×2×3×4=330 б) С84=8×7×6×51×2×3×4=70 Відповідь: а) 330 способів; б) 70 способів 

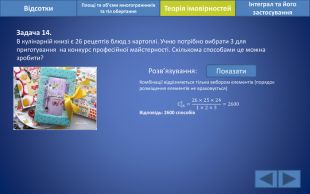
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 14. В кулінарній книзі є 26 рецептів блюд з картоплі. Учню потрібно вибрати 3 для приготування на конкурс професійної майстерності. Скількома способами це можна зробити?Розв’язування: Показати. Комбінації відрізняються тільки вибором елементів (порядок розміщення елементів не враховується) С263=26×25×241×2×3=2600 Відповідь: 2600 способів 

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 15. На виставку робіт кулінарної майстерності потрібно подати 3 муляжа. Учні виготовили 10 муляжів. Скількома способами можна вибрати 6 найкращих для виставки робіт?Розв’язування: Показати. Сполученнями називаються всі можливі комбінації з n елементів по m, які відрізняються одна від одної принаймні хоча б одним елементом . В загальному випадку число сполучень із n елементів по m дорівнює числурозміщень з n елементів по m, діленому на число перестановок з m елементів: С𝑛𝑚=𝐴𝑛𝑚𝑃𝑚=𝑛𝑛−1𝑛−1…(𝑛−𝑚+1)1×2×3×…×𝑚У нашому випадку n = 10, a m = 3 С103=10×9×81×2×3 Відповідь: 120 способів Задача 15. На виставку робіт кулінарної майстерності потрібно подати 3 муляжа. Учні виготовили 10 муляжів. Скількома способами можна вибрати 6 найкращих для виставки робіт?

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 16. У кафе прийшли відвідувачі, сім’я із 6 чоловік. Скількома способами можна посадити 6 гостей на 6 стільцях за одним столом. Розв’язування: Показати. Перестановки відрізняються одна від одної порядком розташування елементів. Число перестановок обчислюємо по формуліРn = n! Так, число перестановок із шести елементів становить Рn = 6! =1× 2 ×3 ×4 ×5× 6 =720 Відповідь: 720 способів

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 17. Дана вибірка жирності молока (в процентах) 3,6; 3,7; 3,4; 3,5; 3,6; 3,7; 2,8; 3,7. Знайти моду и медіану цієї вибірки. Розв’язування: Показати. Мода це те значення випадкової величини, яке зустрічається найчастіше. Позначається Мо. Мо = 3,7 Медіана – це середнє значення впорядкованого ряду значеньвипадкової величини. Позначається Ме. Впорядкуємо ряд: 2,8; 3,4; 3,5; 3,6; 3,6; 3,7; 3,7; 3,7. Ме = 3, 6+3,62 = 3,6 Відповідь: Мо = 3,7; Ме = 3,6 

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 18. Дана вибірка маси(в грамах) семи картоплин: 258, 224, 205, 240, 232, 205, 211. Знайти середнє значення цієї вибірки. Розв’язування: Показати𝟐𝟓𝟖+𝟐𝟐𝟒+𝟐𝟎𝟓+𝟐𝟒𝟎+𝟐𝟑𝟐+𝟐𝟎𝟓+𝟐𝟏𝟏𝟕=𝟐𝟐𝟓 Відповідь: середнє значення цієї вибірки дорівнює 225(грам) 

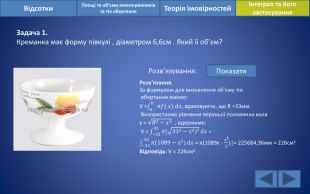
Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 1. Креманка має форму півкулі , діаметром 6,6см . Який її об’єм?Розв’язування: Показати. Розв’язання. За формулою для визначення об’єму тіл обертання маємо: V =𝑎𝑏  𝜋𝑓(𝑥) 𝑑𝑥, враховуючи, що R =33мм. Використаємо рівняння верхньої половинки кола y = 𝑅2−𝑥2 , одержимо: V = −3333𝜋(332−х2)²𝑑𝑥 =−33 33𝜋(1089−х2)𝑑𝑥 = π(1089x - 𝑥ᶾ3)│= 225684,36мм ≈ 226смᶾ Відповідь: V ≈ 226смᶾ 

Відсотки. Площі та об’єми многогранників та тіл обертанняІнтеграл та його застосування. Теорія імовірностей. Задача 2. Експериментально встановлено, що продуктивність праці робітника пекарні наближено виражається функцією:𝑓𝑡=−0,0033𝑡2−0,089𝑡+20,96,де t – робітничий час у годинах. Обчислити обсяг випуску продукції за квартал, вважаючи робочий день восьмигодинним, а кількість робочих днів у кварталі 62. Розв’язування: Показати. Розв’язання. Обсяг випуску продукції протягом зміни є первісною від функції, що виражає продуктивність праці. Тому 𝑉=08𝑓𝑡𝑑𝑡 Протягом кварталу обсяг випуску продукції становитиме: 𝑉=6208𝑓𝑡𝑑𝑡=6208−0,0033𝑡2−0,089𝑡+20,96𝑑𝑡= =62−0,0033𝑡33−0,089𝑡22+20,96𝑡08=62−0,001×512−2,848+167,68==62×164,27≈10185(од)Відповідь: Протягом кварталу обсяг випуску продукції становитиме ≈10185(од.) Закінчити роботу