Позаурочний захід "Математична мозаїка"
 |
П Л А Н
1. Вступна бесіда. Організаційний момент (склад журі).
2. Математична вікторина.
3. Математичні фокуси.
4. Математичні конкурси.
5. Софізми і парадокси.
6. „Народ скаже, як зав’яже”.
7. Шахи і математика.
8. Підведення підсумків.
Добрий день, юні математики!
Сьогодні ми з вами зустрілися, щоб здійснити своєрідну подорож у світ цариці наук – математики.
Можливо, хтось із вас вважає її сухою наукою. Але це не так. В ній є багато цікавого. І наша сьогоднішня мета – показати математику з цієї сторони, розкрити одну з найцікавіших і найпрекрасніших її граней.
В нашій програмі:
вікторини, фокуси, софізми, парадокси, задачі сивої давнини тощо.
В проведенні вечора візьмуть участь усі бажаючі. А допомагатимуть проводити конкурси, роз’яснювати різні деталі розв’язування задач будуть учні 8-го класу.
Для визначення кращих і найактивніших на вечорі нам потрібно обрати журі…
Найактивнішим і найкмітливішим з вас будуть вручені призи.
Отож, рушаймо! А про те, чи цікава математика – судити вам.
Перша зупинка.
Математична вікторина.
1. Котра година, якщо частина доби , що залишилася, вдвічі більша, ніж та, яка пройшла? (Відповідь : 8 годин).
2. Який чотирикутник має тільки :
а) одну вісь симетрії ? (Дельтоїд, рівнобічна трапеція);
б) центр симетрії ? (Паралелограм);
в) центр і дві вісі симетрії ? (Прямокутник чи ромб);
г) центр і чотири вісі симетрії ? (Квадрат).
3.
 У класі 6 учнів. Хлопців з них на 3 більше, ніж дівчат.
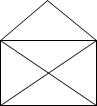
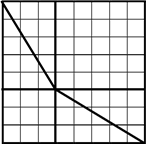
Скільки в класі хлопців і скільки дівчат? (Задача розв’язків не має). 4. Не відриваючи олівця від паперу
і не проводячи жодного відрізка двічі, відтворіть фігуру, зображену на
малюнку.
У класі 6 учнів. Хлопців з них на 3 більше, ніж дівчат.
Скільки в класі хлопців і скільки дівчат? (Задача розв’язків не має). 4. Не відриваючи олівця від паперу
і не проводячи жодного відрізка двічі, відтворіть фігуру, зображену на
малюнку.
5. Користуючись чотирма двійками та знаками дій, запишіть число 111.
(Відповідь : ![]()
Чи багато це?
6. У скільки разів кілометр довше, ніж міліметр ? (У мільйон разів).
7.
Скільки діб становить мільйон хвилин ? (691![]()
8. Крапля води має масу в середньому 0,08 г. Скільки крапель в 1м3 води? (Відповідь: 12,5· 106 крапель).
Задачі на переливання
|
5л |
9л |
|
0 |
0 |
|
0 |
9 |
|
5 |
4 |
|
0 |
4 |
|
4 |
0 |
|
4 |
9 |
|
5 |
8 |
|
0 |
8 |
|
5 |
3 |
9. Як, маючи дві посудини об’ємом 5 і 9 л, набрати з водойми рівно 3 л води? Відповідь :
|
8л |
5л |
3л |
|
8 |
0 |
0 |
|
3 |
5 |
0 |
|
3 |
2 |
3 |
|
6 |
2 |
0 |
|
6 |
0 |
2 |
|
1 |
5 |
2 |
|
1 |
4 |
3 |
|
4 |
4 |
0 |
10. Є три посудини місткістю 8, 5, 1 л. перший з них наповнено водою. Як розлити воду в перші дві посудини так, щоб у кожному було по 4л? Відповідь :
![]()
11.
Маса коропа дорівнює 750 г плюс ![]() того самого коропа. Яка
маса коропа? Відповідь : 3кг
того самого коропа. Яка
маса коропа? Відповідь : 3кг
12. З проволоки, довжиною 16 см, потрібно зігнути контур у вигляді прямокутника, який би обмежував найбільшу площу. Які повинні
бути розміри контура? (Квадрат зі стороною 4 см)
13. Як розкласти 45 горіхів у 9 тарілок, щоб у кожній тарілці була різна кількість горіхів? Відповідь : 1, 2, 3, 4, 5, 6, 7, 8, 9.
Друга зупинка Математичні фокуси
Гральні карти мають деякі специфічні властивості, які можна використовувати при складанні фокусів математичного характеру.
1. Назвіть яке-небудь число між 10 і 20.
Відкладається одна за одною ця кількість карт у кучку. Потім знаходиться сума цифр цього числа і знімається зверху кучки це число карт, рівне цій сумі, і кладеться назад на гору колоди. Карта, яка опинилася зверху кучки, відкладається в сторону лицьовою стороною, а всі останні карти кучки повертаються на гору колоди.
Знову назвіть любе число між 10 і 20. Повторюється та сама комбінація. Так 3-й і 4-й рази. Відкриваємо ці 4 карти і всі вони – тузи.
Пояснення
Перед початком фокуса тузи треба покласти на : 9-е, 10-е, 11-е, 12-е місця зверху. Далі фокус виходить автоматично.
2. А ось старовинний фокус, в якому використовується числове значення монети.
Хто-небудь повинен взяти в один кулак гривенник ( 10 к.), а в другий – одну копійку.
Помнож число копійок у правому кулаці, наприклад, на 8 ( або на любе парне число), а число копійок у лівому – на 5 (або на любе непарне число).
Тепер додай ці два числа і скажи : непарне чи парне одержане число? Після цього треба сказати, яка монета в якій руці.
Пояснення
Якщо сума парна, то у правій руці – 1 копійка ( тоді у лівій руці – 10 копійок).
Якщо сума непарна, то у правій руці – 10 копійок (тоді у лівій – 1 копійка).
3. Тепер ми покажемо фокус типологічного характеру.
Типологія вивчає такі властивості тіл ( предметів), які не змінюються при неперервних розтягах і стисках.
Вивертання жилету навиворіт
Чи можна вивернути жилет навиворіт не рознімаючи пальців? Пальці глядач з’єднує перед собою, витягнувши руки вперед.
МОЖНА!
Розстебніть жилет і підніміть його над головою так, щоб він повис на руках. Вивернути там навиворіт, просовуючи через один з отворів для рукавів, і зрештою надіти жилет знову.
Те саме можна проробити і з не розстебнутим жилетом. Можна також і зняти жилет, не знімаючи піджака.
Третя зупинка Софізми і парадокси
Софізми – це міркування, в яких строго логічними, на перший погляд, способами доводиться, що двічі по два – п’ять, що частина більше від цілого і т. д.
Парадокси – це твердження (думка), яка розходиться з загальновизнаним, а також суперечить ( іноді тільки на перший погляд) здоровому глузду.
Геометричний софізм
1. Площа знайома і несподівана.
Задачі на розрізування фігур і складання з отриманих частин якихось інших фігур традиційно займають почесне місце в цікавій математиці.
Візьмемо квадрат, площа якого
дорівнює 64, (8×8) – звичайна шахова дошка і розріжемо дану фігуру на три
частини, так як на малюнку. Переклавши їх, дістанемо рівноскладений з даним
квадратом прямокутник. Таким чином, із квадрата, площа якого 64, дістали
прямокутник, площа якого дорівнює ![]() ( 63=64!?)
( 63=64!?)
Відповідь : маленький прямокутний трикутник не буде рівнобедреним.
Справді, ![]() і
і ![]() . Тому
. Тому ![]() ,
,
![]() . Довжина основи
цього прямокутника дорівнює не 8+1, а
. Довжина основи
цього прямокутника дорівнює не 8+1, а
![]() , а його площа
, а його площа ![]() .
.
Все ж таки : 64 = 64 !
Арифметичний софізм „Перші несподіванки”
Доведемо, що 1=2
2 = 2;
3-1 = 6-4;
1-3 = 4-6;
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Отже : 1=2
Відповідь : цей софізм заснований на неправомірному поширенні істинності прямої теореми: „Якщо числа рівні, то й квадрати їх рівні”, та обернену „ Якщо квадрати двох чисел рівні, то й ці числа рівні”.
На множині натуральних чисел справджується пряма і обернена теореми. На множині ж цілих чисел пряма теорема справджується, а обернена – ні. Істинним є частково стверджувальне висловлення : „Якщо квадрати двох чисел (цілих) рівні, то й ці числа можуть бути рівними”.
Останні перетворення мали бути такими:
![]() ;
;
![]() ;
;
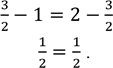 ;
;
Невизнані правила арифметики
Ви, юні друзі, звичайно, пам’ятаєте основні правила дій над натуральними числами, цілими і дробовими числами. Спробуємо ввести ще деякі правила.
Розширимо можливості скорочення дробів, наприклад, такими способами:
![]() ;
;
![]()
або: ![]() ; можна і так :
; можна і так : ![]() .
.
Відповідь : справді існують окремі види дробів, у яких можна „по– варварськи” закреслювати в чисельнику і знаменнику „ зайві” цифри, не змінюючи величину дробу. Такі скорочення тільки для дробів виду:
 , у яких
, у яких ![]() ,
, ![]() ;
;
![]() .
.
Усього таких дробів існує 120 штук.
Крім того,
скорочення цього типу можливі для дробів: 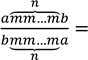
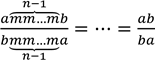 ; де
; де ![]() ,
, ![]() .
.
Цей випадок
зводиться до попереднього при: ![]() .
.
Існує тільки 16 дробів такого виду.
Четверта зупинка
Математичні конкурси
1. „Хто перший подолає лабіринт?”
2. „Хто швидше порахує до 40?”
П’ята зупинка „ Народ скаже, як зав’яже”
Численні афоризми і мудрі сентенції народів свідчать про споконвічне прагнення людини до знань. Віками позбавлений можливості одержувати систематичні шкільні знання, народ використовував з освітньою метою засоби усної народної творчості.
Велике місце в розвитку математичного мислення молоді посідали різноманітні задачі й головоломки.
Народна математика широко використовується в предметно – практичній діяльності людини – від арифметичних розрахунків до складних і не завжди розшифрованих геометричних побудов у архітектурі, при закладанні нових міст, а також реконструкції старих.
Учені виявили в народній математиці задачі, які прийшли з глибокої давнини і буквально мандрували по світу від одного народжу до іншого.
Ці витвори народної мудрості не втратили свого освітнього потенціалу і в наш час.
Деякі з цих задач пропонуємо вашій увазі.
1. Летіли горобці, сіли на стовпці, сядуть по два – один стовпець зайвий, як сядуть по одному – один горобець зайвий. Скільки горобців і скільки стовпців? (4 горобці і 3 стовпці)
2. Пасли два хлопці поросят, один і каже другому: „ Дай мені одне порося, то в нас буде порівну”. А другий каже: „Дай мені ти одного, то в мене буде якраз вдвічі більше, ніж у тебе”. По скільки було в них поросят? (5 і 7 поросят)
3. П’ять, п’ятнадцять, без двох двадцять, семеро, троє, ще й малих двоє. Скільки всіх? (50)
4. Стоїть стовп, а на стовпі сорок кілець. До кожного кільця прив’язано по сорок кобил, у кожної кобили по сорок лошат. Скільки всіх лошат?
(64000)
5. У хлопчика стільки сестер, скільки й братів, а в його сестри сестер вдвоє менше,ніж братів. Скільки в сім’ї сестер та братів? (4 брата і 3 сестри)
6. Дуже давно на Сході жив-був чоловік, який вмираючи залишив своїм трьом синам сімнадцять верблюдів. Він заповів старшому сину половину, середньому – третину, молодшому – дев’яту частину.
Не розв’язавши самостійно (адже задача в цілих верблюдах розв’язку не має), брати звернулися до мудреця.
– О, мудрий! – сказав старший брат. – Батько залишив нам сімнадцять верблюдів і велів розділити між собою таким чином… . Але 17 не ділиться ні на 2, ні на 3, ні на 9. Чи зможеш ти, о вельмишановний, допомогти нашій біді, бо ми хочемо виконати волю батька?
– Нема нічого простішого, – відповів мудрець, – якщо до 17 ваших чудових приєднати ще й мого старенького верблюда. Ось слухайте.
Брати слухали й дуже дякували мудрецю, який задовольнив всі умови батьківського заповіту і не випадково, замість свого старенького сів, щоб їхати далі, на найкращого з верблюдів. Як розділив мудрець спадщину? (Старшому – 9, середньому – 6, молодшому – 2 верблюди).
ПОЯСНЕННЯ
![]()
![]() Батько склав заповіт непередбачливо: сума
Батько склав заповіт непередбачливо: сума ![]() , а не 1. Точне
виконання заповіту, якщо не рахуватися з вимогами доцільностіі практичної
реалізації, передбачає передачу старшому синові
, а не 1. Точне
виконання заповіту, якщо не рахуватися з вимогами доцільностіі практичної
реалізації, передбачає передачу старшому синові ![]() верблюдів, середньому
–
верблюдів, середньому
– ![]() ,
молодшому –
,
молодшому – ![]() , що становить
, що становить ![]() , а
, а ![]() від одного верблюда
залишається поза розподілом. Мудрець підмінив умови заповіту, приєднавши до
спадщини свого верблюда. Тоді старший отримав
від одного верблюда
залишається поза розподілом. Мудрець підмінив умови заповіту, приєднавши до
спадщини свого верблюда. Тоді старший отримав ![]() верблюдів, середній –
верблюдів, середній – ![]() верблюдів,
а молодший
верблюдів,
а молодший
– ![]() верблюди.
верблюди.
Але такий розв’язок не є точною
реалізацією заповіту, а лише доцільним наближенням до його вимоги. Старший син
фактично одержав більше на ![]() верблюда, середній – на
верблюда, середній – на ![]() верблюда, а
молодший на
верблюда, а
молодший на ![]() . Ці надбавки в сумі вичерпують
. Ці надбавки в сумі вичерпують ![]() верблюда, які
згідно із заповітом залишилися поза розподілом.
верблюда, які
згідно із заповітом залишилися поза розподілом.
Шоста зупинка Шахи і математика
У математики і шахів багато спільного. Видатний математик Харді, проводячи паралель між цими двома видами людської діяльності відмічав, що розв’язання проблем шахової гри є не що інше, як математична вправа, а гра у шахи – це нібито насвистування математичних мелодій. Форми мислення математика і шахіста дуже близькі, і не випадково математичні здібності нерідко добре пасують з шаховими. Наведемо деякі приклади цього переплетіння.
Приклад 1
 Обговорюючи математичні властивості шахової
дошки, не можна не згадати про одне, дуже старе доведення на шаховій дошці…
теореми Піфагора.
Обговорюючи математичні властивості шахової
дошки, не можна не згадати про одне, дуже старе доведення на шаховій дошці…
теореми Піфагора.
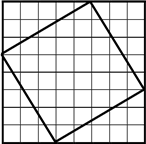
Розіб’ємо дошку на квадрат і чотири однакових прямокутних трикутники.(див. мал.a). На мал.б зображені ті ж самі трикутники і два квадрати.
 Трикутники в обох випадках
займають одну й ту ж саму Мал. а площу. А значить одну й ту ж
саму площу займають частини дошки без трикутників, що залишилися (на мал.а) – 1 квадрат, а на мал.
б – 2 квадрати. Оскільки більший квадрат побудовано на гіпотенузі прямокутного
трикутника, а маленькі – на його катетах, то видатна теорема Піфагора доведена!
Трикутники в обох випадках
займають одну й ту ж саму Мал. а площу. А значить одну й ту ж
саму площу займають частини дошки без трикутників, що залишилися (на мал.а) – 1 квадрат, а на мал.
б – 2 квадрати. Оскільки більший квадрат побудовано на гіпотенузі прямокутного
трикутника, а маленькі – на його катетах, то видатна теорема Піфагора доведена!
Мал. б
Приклад 2
Оповідання про коня – хамелеона.
Мова піде про задачу, в якій треба прокласти маршрут коня через усі поля шахової дошки, але так, щоб кінь побував у кожній клітинці тільки один раз (часто цю задачу називають просто задачею про хід коня).
Особлива популярність цієї задачі пояснюється тим, що у ХVІІІ і ХІХ століттях нею займались видатні математики, в тому числі й великий Леонард Ейлер, який присвятив їй мемуар „Розв’язання одного цікавого питання, яке, нібито не піддається ніякому дослідженню”. Задача була відома і до нього, але він уперше звернув увагу на її математичність. розв’язків цієї задачі дуже багато, більше 30 мільйонів. Відомо багато методів для знаходження маршрутів коня. Ці методи носять імена тих, хто першим відкрив їх: метод Ейлера і Вандермонда, рамочний метод Мунка і Колліні, метод ділення на чверті Поліньяка і Роже та ін.
Ось найпростіше правило побудови маршрута коня.
Правило Варнсдорфа: при обході дошки коня слід кожен раз ставити на поле, з якого він може зробити найменше число ходів на поля, на яких він ще не бував. Якщо таких клітинок декілька, то можна вибрати будьяку з них.
Цьому правилу понад 150 років.
Якщо вести розмову про графіки маршрутів коня, то тут – ціла множина незвичайних розв’язків, які зображують різні предмети, букви і знаки. Відомий навіть графік, присвячений Наполеону.
Підведення підсумків.


про публікацію авторської розробки
Додати розробку
