Застосування формул зведення

Навчально – методична карта заняття

Предмет : математика

Тема заняття: формули зведення

Тривалість заняття: 2 год

Тип заняття: комбінований

Група: І курс, «Лікувальна справа», «Сестринська справа»

І. Актуальність теми:

 Тригонометричні функції необхідні для опису різних періодичних процесів. Людину постійно супроводжують явища та процеси, які періодично повторюються:

     Для всіх цих процесів одне спільне – вони періодичні, і описують їх тригонометричні функції.

ІІ. Навчальні цілі заняття:

 Студент повинен:

 Знати:

• Співвідношення між різними  тригонометричними функціями
• Формули зведення тригонометричних функцій

    Вміти:

• Розрізняти основні тригонометричні функції
• Застосовувати формули зведення тригонометричних функцій

ІІІ. Цілі розвитку особистості (виховні):

• Виховання в учнів культури математичної мови;
• Розвивати самооцінку
• Прививати інтерес до вивчення математики.

ІV. Міждисциплінарна  інтеграція:

 Забезпечуючі дисципліни:

Інформатика, фізика.

V.Зміст теми заняття

Зміст теми заняття:

VІ.Зміст заняття

 Сприймання і усвідомлення формул зведення.

Тригонометричні функції чисел виду ± α, π ± α; ± α, 2π ± α можуть бути виражені через функції кута α за допомогою формул, які називаються формулами зведення.

Користуючись формулами тригонометричних функцій суми (різниці) двох чисел, можна довести формули зведення:

для синуса

для косинуса

для тангенса і котангенса

Формули зведення запам'ятовувати необов'язково. Для того щоб записати будь-яку з них, можна користуватися таким прави­лом:

1) В правій частині формули ставиться той знак, який має ліва частина при умові 0 < α < .

2) Якщо в лівій частині формули кут дорівнює ± α, ± α, то  синус замінюється на косинус, тангенс — на котангенс і на­впаки. Якщо кут дорівнює π ± α, то заміна не виконується.

Розглянемо приклади.

Приклад 1. Виразимо tg(π – α) через тригонометричну функцію кута α. Якщо вважати, що α — кут І чверті, то π – α буде кутом II чверті. У II чверті тангенс від'ємний, отже, у правій частині рівності слід поставити знак «мінус». Для кута π – α назва функції «тангенс» зберігається. Тому.

tg (π – α) = - tg α.

За допомогою формул зведення знаходження значень триго­нометричних функцій будь-якого числа можна звести до знаходження значень тригонометричних функцій чисел від 0 до .

Приклад 2. Знайдемо значення sіn .

Маємо: .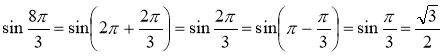

Виконання вправ______________________________

1. Приведіть до тригонометричних функцій числа а:

а); б);  в) сtg (π – α); г) tg (π + α); д) sіn (π + α); є).

Відповідь: а) соs α; б) - sіn α; в) - ctgα; г) tg α; д) - sіn α; є) сtg α.

2. Знайдіть:

а) sіn ;     б) соs ;     в) tg ;      г) sіn .

Відповідь: а) ;  б) - ;  в) - ;   г) .

3. Спростіть:

а) 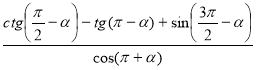; б) .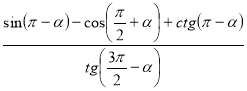

Відповідь: а) 1. б) –1.

4. Доведіть, що

а) ,   б) .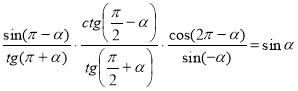

VІІ. ЛІТЕРАТУРА

1. Алгебра і початки аналізу. Підруч. для 10–11 кл. серед, шк. / А. М. Колмогоров, О. М. Абрамов, ІО. П. Дудніцин та ін.; За ред. А. М. Колмогорова. – К.: Освіта, 1992. - 350 с.
2.  Бевз Г. П. Методика розв'язування алгебраїчних задач. - К.: Рад. шк., 1975. - 240 с
3. Бевз Г. II., Бевз В. Г., Владимирова II. Г. Геометрія: Проб, підруч. для 10 - 11 кл. загальноосвітніх навч. закл. - К.: Вежа, 2002. - 223 с.