.                         

                Практичні роботи з алгебри, 7 клас

 

Уся глибина думки, закладена

В формуванні математичних понять,

Згодом розкривається тим умінням,

Із яким  ці поняття використовуються

Е. Вінгер

 

Пояснювальна записка

 

Закон України “Про загальну середню освіту” потребує нових форм і методів організації  навчання та контролю знань, сучасної системи оцінювання навчальних   досягнень учнів.

З метою допомоги вчителю,   складено практичні завдання.

Ці завдання  допомагають вчителеві перевірити рівень засвоєння учнями знань, умінь і навичок. Допоможуть учням формувати практичні навички з використанням теоретичних знань. Розвивати творчі здібності. Виховувати самостійність та інтерес до математики.

Практичні роботи розраховані для домашньої роботи, індивідуальної та парної роботи в класі, на уроках узагальнення і систематизації знань і вмінь. Пропонуються завдання пошукового, прикладного творчого характеру.

Тема 1.  Лінійні рівняння з однією змінною

 

Практична робота

(для домашнього виконання)

 

1. Дати відповідь на запитання.
   • Що називається рівнянням?
   • Що таке корінь рівняння?
   • Що значить розв’язати рівняння?
   • Які рівняння називаються рівносильними?
   • Властивості рівнянь.
   • Які рівняння називаються лінійним?

 

2. Виписати:

1) лінійні рівняння.

а) –х=5; б)  1/х=2; в) 3-2х=0; г) 4х=5-х; д) 3х=2; е) 2х²=3.

2) рівносильні рівняння:

а)  3х+2х=15 і 5х=15;                         б) 3х-15=0 і 3х-1=14;

в) 4х+3=2х-1 і 6х=-50;                        г) 5х-4=11 і –7х=49.

 

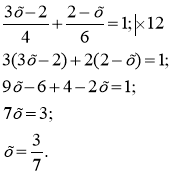3. Знайти помилки в розв’язанні рівнянь, виправити їх і записати правильне розв’язання.

а) 4у-3(20-у)=6у-7(11-у);        б)

    4у-60-3у=6у-77+7у;

    4у-3у-6у-7у=-77+60;

    -12у=-17;

 

 

 

4. Задача.

В одній крамниці було в 2 рази більше картоплі, ніж у другій. Коли перша крамниця продала 12 ц картоплі, а друга  - 5 ц, то в обох крамницях картоплі стало порівну. Скільки центнерів картоплі було у кожній крамниці спочатку?

Заповнити таблицю і розв’язати задачу.

	Було, ц	Стало, ц	Рівняння
І крамниця
ІІ крамниця	х

 

5. Скласти рівняння до задачі за її  короткою умовою

І школа      у 2,  рази менше, ніж

ІІ школа                                                                     3080 учнів

ІІІ школа   на 80 Учнів більше, ніж

 

6. Скласти рівняння:

а) які рівносильні рівнянню 2х=-3

б) мають корінь 7

 

7. Скласти задачу, яка розв’язується за допомогою рівнянь.

Тема 2. Вирази зі степенями

Тип уроку: Узагальнення і систематизація

 

Практична робота виконується на уроці

(робота в парах)

 

1. Записати основні вивчені поняття (вирази, числові вирази, вирази зі змінними, вирази з степенями...)   та побудувати блок-схему.
2. Скласти вираз за умовою задачі та знайти його значення

Мишко знайшов 12 грибів, а Борис на 6 грибів більше. Скільки грибів зібрали обидва хлопці?

3. Заповніть таблицю

	1	2	3	4	5	6	7	8	9	10
2n
3n

 

4. Встановити відповідність між виразом та його значенням.

 

А) 2,37+4,23-13,7 х  0,1	1) 8,5
Б) 3х+8, якщо	2) 4
В) 2х2-2, якщо  х=3	3)  5,23
Г) 0,512 х 213	4) 16
Д)	5) 2

 

5. Скласти кросворд з термінів теми.

 

 

 

 

Тема 3. Одночлени

 

Практична робота

(індивідуальна робота на уроці протягом 10 хв.)

 

1. Наведіть власний приклад одночлена та виразу, який  не є одночленом.

 

2. Випишіть одночлени стандартного вигляду і підкресліть їх коефіцієнти.

а) 4 ху;          б) -5аbа;       в) 7m²nm³n;   г) –а⁷b⁹;

д) 0,3рх3m;  е) -2abc ;       є) a⁹b⁷;           ж) 14.

 

3. Розгляньте приклади. За наведеними розв’язаннями  складіть алгоритм:

а) множення двох (і більше) одночленів;

б) піднесення одночлена до степеня.

1) 2х³0,5 ху² = (20,5) (х³х) у² =х⁴ у²

2) (2х³ у)⁵ =2⁵ (х³)⁵    у⁵ =32х¹⁵ у⁵

 

4. Поставити замість * одночлен стандартного  вигляду, щоб отримати правильну рівність.

а) * х 4m²n =12m⁷n¹² ;

б) 5 m²a³ x * =-5m²a³ ;

в) –7p² x³ x * = 21 p² x⁹;

г) (*) = 4 m⁶ ;

д)   *  x (-5a²b) =a³b;

е) (*)² = 100 c⁶m¹²

Тема 4. Многочлени

Тема 4.1. Многочлени. Додавання і віднімання многочленів

 

Практична робота

(виконується на уроці при роботі в малих групах)

1. Складіть многочлен із одночленів
   1. 5m і –5n;
   2. m³,  -2m²  i mn;
   3. –x³,  -2y² , xy і 4
2. Підставте в запис пропущені знаки та закінчіть перетворення, обґрунтувавши свою відповідь:

1) ...2а²b- … … …5a²b+2a…=2a²b2--5a²b-2a=…

2) …-5x²+2xy – 4 …  … … 4x²-6xy…=-5x²+2xy-4+4x²-6xy=…

3. Замініть зірочку многочленом так, щоб утворилась тотожність

а) *- (8а³-2а² +7) =3-а²

б)  * +(3х+8)=-3х²+2х-15

в) (2 ху-11х²+10у²)- *=5х² + 4у²-6

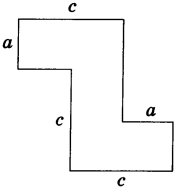4. Визначити периметр фігури    

 

 

 

 

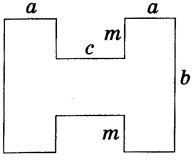
5. Розв’яжіть задачу.

Робітник працював 4 год. За першу годину він виготовив а деталей, а за кожну наступну на 2 деталі менше, ніж за попередньою. Скільки деталей виготовив робітник:

1. за другу годину;
2. за третю годину;
3. за перші три години;
4. за останні три години.

Тема 4.2 Множення одночлена на многочлен та множення многочленів.

 

Практична робота

(для домашнього виконання)

1. Скласти схеми:

а) множення одночлена на многочлен

б) множення многочленів.

2. Заповнити пропуски:

а) –4х²(*-*)=2х³  +12х⁴;

б) (-х²+*) х (-6х)=*+42х⁵;

в) (2m³-9m) x *= 10m⁶ -*;

г)  (x-1) (*+3)=x² +*-*

д)  (y+2) (y-*)= *+y-*

3. Ідентифікуйте рівняння і відповідний йому корінь:

А) 3(2х-5)+7(3х-4)=3х+77	1)	А
Б)	2)	Б
В) 5(8у-1)-7(4у+1)+8(7-4у)=19	3) 0	В
Г) (х-1)(х+5)=(х-2)(х+3)	4) 5	Г
Д) 0,5с2 –(0,5-1)(с+2)=1	5)	Д

 

4. Розв’яжіть задачу.

Одна сторона прямокутника в 4 рази більша за другу. Якщо меншу сторону збільшити на 3 см, то площа прямокутника збільшиться на 24 см². Знайти сторони  прямокутника.

 

5. Скласти кросворд використовуючи терміни даної теми.

 

 

Тема 5. Формули скороченого множення

 

Практична робота

виконується на уроці узагальнення знань і вмінь при роботі в парах

1. Записати формули різниці квадратів, квадрата двочлена і суми та різниці кубів.

 

2. Заповнити таблицю.

Вираз І	Вираз ІІ	Квадрат суми і  різниці виразів І і ІІ	Різниця квадратів виразів І і ІІ	Куб суми виразів І і ІІ	Сума кубів виразів І і ІІ	Різниця кубів виразів І і ІІ
2х	b
2х	7b
3х	1/3b
0,5х	4b
1/2х	8b

 

3. Вставити одночлен замість *, щоб утворилась тотожність.

а) (*+2а)² =b²+4ab+4a

б) (5x²-*)²=25x⁴ -*+9m²

в) (*-9p)(*+9)=0,25m⁴-81p²

г) *-b³c⁶=(a-*)(a²+*+b²c⁴)

д) (*+2q)³=(p³ +6 p²q+*+*)

 

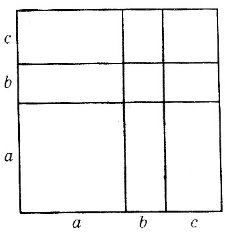
4. Користуючись малюнками поясніть геометричний зміст формули

(а+b+ c)²=a²+ b²+ c²+ 2ab +2ac +2bc

Тема 6. Розкладання многочленів на множники різними способами

 

Практична робота

пропонується для домашнього розв’язання

1. Які є способи розкладання многочленів на множники?  (перерахувати способи і до кожного записати свій власний приклад)

 

2. Розгляньте приклад.

За наведеним розв’язанням складіть алгоритм розкладання його на множники:

аm⁴ -m⁴- am²+ m²=m²(am²-m²-a+1)=m²(m²(a-1)-(a-1))=m²(a-1)(m²-1)=m²(a-1)(m-1)(m+1)

 

3. Замініть у виразі один із коефіцієнтів так, щоб отриманий тричлен можна було подати у вигляді квадратного двочлена (виконайте завдання трьома  різними способами)
   1. 100m²+ 40 mn + n²
   2. 25a²- ab +9b²
4. Знайдіть  помилки у розв’язанні прикладів та наведіть правильне розв’язання

а)  25-c⁶ = (5-c⁶)(5+c⁶)

б) 0,01-x²=(0,01-x)(0,01+x)

в) a²+2 am+ m²= (a²+ m²)²

г) b²-6b+9=(b+3)²

д) 27-b³= (27-b)(27² +27b +b²⁾

е) 8х³+1= (2х+1)(4х²+2х+1)

5. Підібрати вправи на обчислення, в яких використовується розкладання многочленів на множники

 

6. Відшукати історичні відомості про правила скороченого множення

Тема 7. Функції

Практична робота

(домашня робота) виконується в групах

1. Яка із залежностей є функцією?

а)  m=2n²-5   

б) y=x³–x²-3

в) ab + a² + b²=0

г) x + y= xy

д)

е)

2. Які з функцій – лінійні, які – задають пряму пропорційність?

а) y =-3x

б) y=-3x+4

в) y=-3x+4x²

г) y=-3

д)

е)

3. Ідентифікуйте до  кожного значення аргументу відповідне значення функцій, якщо функцію задано формулою 

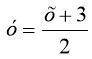
А)  х=1	1) 1,5	А
Б) х=-3	2) 2	Б
В) х=11	3) –1,5	В
Г) х=-6	4) 7	Г
Д) х=0	5) 0	Д

 

 

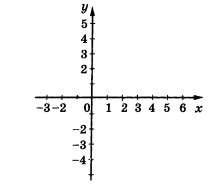
4.Вкажіть, на якому малюнку зображено графік функцій  у =-3х+1

5. Розв’яжіть задачу.

Із села до міста, віддаленого на відстані 48 км, вирушив велосипедист зі швидкістю 14 км/год. Задати формулою залежність змінної  S  від змінної   t, де S  - відстань велосипедиста до міста (у км), а  t – час його руху (у год/). 

Знайдіть за формулою:

1)  S, якщо t=1,5                                                      

2)  t, якщо S =13

6.Запишіть формули функцій, графіки яких зображені на малюнку.

 

 

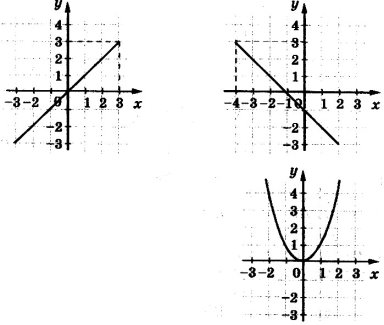7. Функцію задано графічно. Для кожного з випадків (а- b)  складіть таблицю деяких значень. Задайте функції формулами.

 

 

 

 

 

 

 

 

 

8. Підготувати  проект на тему “Функціональна залежність в житті людини”.

Тема 8. Системи лінійних рівнянь

 

Практична робота  №1

(індивідуальна) виконується в класі

1. Скласти будь-яке лінійне рівняння за двома змінними:

а) розв’язком якого є пара чисел  х=3, у=-2.

б) графік якого проходить через точку Р(1;-3)

2.  Скласти систему лінійних рівнянь з двома змінними, розв’язком якої є пара чисел  (1;-3)
3. Розгляньте розв’язок системи і складіть алгоритм її  розв’язання:

а)

4(1+7у)+3 х 9у=3 х 38,

4+28у+27у=114,

55у=110,

у=2,

Відповідь: (5;2)

б)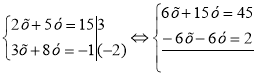              

                                              

2х+5 х (-47)=15,

2х-235=15,

2х=250,

х=125

Відповідь:  (125;4)

4. Скласти задачу, яка розв’язується за допомогою системи рівнянь.

2х+3у=15

х-у=1

Практична робота №2

(виконується в групах, як довготривала домашня робота)

 

1. Підготувати збірку історичних відомостей про способи розв’язання систем рівнянь.
2. Скласти кросворд з термінів даної теми.
3. Створити проект „Поезія в задачах, які розв’язуються за допомогою систем  рівнянь”.

 

 

 

 

Тема 9. Повторення вивченого матеріалу.

 

Практична робота

довготривалого характеру виконується в групах

1. Скласти схему зв’язків між темами вивченими у 7 класі.
2. Скласти кросворд з алгебраїчних термінів, які вивчалися протягом року.
3. Підготувати презентацію на тему:

1. «Математика в фізиці» ( I група);
2. «Математика в хімії» ( II група);
3. « Математика в географії» ( III група).