Практико-орієнтований урок "Дослідження квадратичної функції"

Про матеріал

В даному конспекті уроку запропонований практико-орієнтований підхід. Учні під час виконання практичних завдань досліджують властивості квадратичної функції, вивчають алгоритм її побудови, зясовують способи розміщення графіка в залежності від виду функцїі.

Перегляд файлу

Тема: дослідження квадратичної функції, її графіка.

Мета: дослідити всі можливі випадки розміщення графіка квадратичної функції, її властивості; формувати вміння проектної діяльності, розвивати алгоритмічну культуру учнів, уміння класифікувати; стимулювати активну пізнавальну діяльність, розвивати креативне мислення, створювати ситуації успіху, виховувати самостійність, упевненість у своїх силах. Здатність до подолання труднощів.

Набуття ключових компетентностей. Мовленнєва

- Правильно вживає математичні терімни

- Розуміє важливість чітких формулювань Математична:

- Володіє графічною інформацією

- Знає математичні поняття, вільно оперує з ними

Соціальна та громадянська

- Вчиться працювати в команді

Тип уроку: урок формування компетентностей, практично-орієнтований урок.

Хід уроку.

І. ПОВІДОМЛЕННЯ ТЕМИ, МЕТИ, ЗАВДАНЬ УРОКУ.

ІІ. ФОРМУВАННЯ НОВИХ КОМПЕТЕНОСТЕЙ.

Робота в групах.

1. З даних функцій, користуючись означенням, вибрати квадратичні. ( Один учень-експерт надає означення квадратичної функції.

у= х³+2х-3 у= х²-4 у= х-1 у= 6х²+2х-3 у=х²+4х-1 у=х²+4х у=х⁶-9

2. Учні отримують картки з функціями і їх графіками і з’ясовують, від чого залежить напрям віток параболи

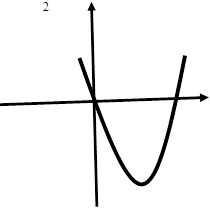У= 3х -9х

Учні роблять висновок, що напрям віток параболи залежить від знаку коефіцієнта а.

3. Учні отримують картки з алгоритмом побудови графіка квадратичної функції та виконують завдання Алгоритм:

- Знаходимо координати вершини параболи, яка є графіком даної функції за формулами х_в= - ^𝑏 y_в = ^{4𝑎𝑐−𝑏²}

2𝑎 4𝑎

- Визначаємо напрям віток параболи

- Проводимо через побудовану вершину вісь симетрії параболи – пряму, паралельну осі ОУ

- Знаходимо ще декілька точок параболи. Для цього беремо декілька значень х, які лежать близько до вершини, та знаходимо у, підставляючи в функцію ці значення. Отримуємо координати декількох точок параболи.

- Через побудовані точки проводимо параболу. Зверніть увагу, що вітки повинні бути симетричні відносно осі симетрії.

Побудувати графік квадратичної функції: у= х² +4х+3 у=-х²+5х-3,25 у=х²-4х+4

4. Групи отримують завдання: знайти дискримінант рівняння, отриманого з власної квадратичної функції та з’ясувати залежність між кількістю нулів функції ( кількістю перетину графіком вісі ох) та значенням дискримінанта у= 2х²-6х+1 у=-3х²+12х+1

у=3х²-6х+2 За підсумками виконання завдання вони заповнюють таблицю (рисунками параболи або записом кількості нулів у кожному випадку)