Правила обчислення похідних
Про матеріал
Презентація "Правила обчислення похідних" призначений для учнів 10 класу, які вивчають алгебру на профільному рівні. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
-
Дякую!
pptx
До підручника
Алгебра і початки аналізу (профільний рівень) 10 клас (Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку











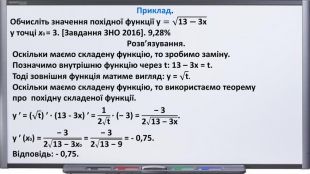
![Приклад. Обчисліть значення похідної функції у=13 − 3х у точці x0 = 3. [Завдання ЗНО 2016]. 9,28%Розв’язування. Оскільки маємо складену функцію, то зробимо заміну. Позначимо внутрішню функцію через t: 13 – 3х = t. Тоді зовнішня функція матиме вигляд: у = t. Оскільки маємо складену функцію, то використаємо теоремупро похідну складеної функції.у ʹ = (t) ʹ · (13 - 3х) ʹ = 12t· (− 3) = − 3213 − 3х. у ʹ (x0) = − 3213 − 3x0 = − 3213 − 9 = - 0,75. Відповідь: - 0,75. Приклад. Обчисліть значення похідної функції у=13 − 3х у точці x0 = 3. [Завдання ЗНО 2016]. 9,28%Розв’язування. Оскільки маємо складену функцію, то зробимо заміну. Позначимо внутрішню функцію через t: 13 – 3х = t. Тоді зовнішня функція матиме вигляд: у = t. Оскільки маємо складену функцію, то використаємо теоремупро похідну складеної функції.у ʹ = (t) ʹ · (13 - 3х) ʹ = 12t· (− 3) = − 3213 − 3х. у ʹ (x0) = − 3213 − 3x0 = − 3213 − 9 = - 0,75. Відповідь: - 0,75.](/uploads/files/1340045/239497/258937_images/11.jpg)



![Приклад. Матеріальна точка рухається за законом s(t) = t2 + 4t + 2 (час t вимірюють у годинах, шлях s – у кілометрах). У який момент часу швидкість точкидорівнює 7 км/год? [Завдання ЗНО 2008]. Розв’язування. Оскільки sʹ(t) = v(t), то v(t) = (t2 + 4t + 2)ʹ == 2t + 4. Враховуючи, що за умовою v(t) = 7, маємо рівняння 2t + 4 = 7, звідки t = 1,5. Відповідь: 1,5 год. Приклад. Матеріальна точка рухається за законом s(t) = t2 + 4t + 2 (час t вимірюють у годинах, шлях s – у кілометрах). У який момент часу швидкість точкидорівнює 7 км/год? [Завдання ЗНО 2008]. Розв’язування. Оскільки sʹ(t) = v(t), то v(t) = (t2 + 4t + 2)ʹ == 2t + 4. Враховуючи, що за умовою v(t) = 7, маємо рівняння 2t + 4 = 7, звідки t = 1,5. Відповідь: 1,5 год.](/uploads/files/1340045/239497/258937_images/15.jpg)
![Приклад. Функція f(х) має в точці х0 похідну f '(х0) = - 4. Визначте значення похідної функції g(х) = 2 · f(х) + 7x – 3 в точці х0. [Завдання ЗНО]. Розв’язування. gʹ(х) = (2 · f(х) + 7x – 3)ʹ = 2 · f ʹ(х) + (7x – 3)ʹ = 2 · f ʹ(х) + 7. gʹ(х0) = 2 · f ʹ(х0) + 7 = 2 · (− 4) + 7 = - 1. Відповідь: - 1. Приклад. Функція f(х) має в точці х0 похідну f '(х0) = - 4. Визначте значення похідної функції g(х) = 2 · f(х) + 7x – 3 в точці х0. [Завдання ЗНО]. Розв’язування. gʹ(х) = (2 · f(х) + 7x – 3)ʹ = 2 · f ʹ(х) + (7x – 3)ʹ = 2 · f ʹ(х) + 7. gʹ(х0) = 2 · f ʹ(х0) + 7 = 2 · (− 4) + 7 = - 1. Відповідь: - 1.](/uploads/files/1340045/239497/258937_images/16.jpg)