Правила з геометрії 10 клас які вам точно знадобляться

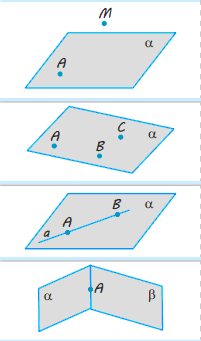
Аксіома 1. Яка б не була площина, існують точки, що належать цій площині, і точки, які не належать їй.

 Аксіома 2. Через будь-які три точки, які не лежать на одній прямій, можна провести площину, і до того ж тільки одну.

 Аксіома 3. Якщо дві різні точки прямої лежать у площині, то і вся пряма лежить у цій площині.

Аксіома 4. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку.

 Аксіома 5. Відстань між будь-якими двома точками простору одна і та сама на всіх площинах, що містять ці точки .

Означення. Дві прямі в просторі називаються мимобіжними, якщо вони не лежать в одній площині.

Означення. Дві прямі в просторі називаються паралельними, якщо вони лежать в одній площині і не перетинаються.

Означення. Пряма і площина називаються паралельними, якщо вони не мають жодної спільної точки.

Означення. Дві площини називаються паралельними, якщо вони не перетинаються.

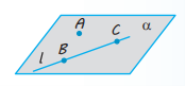
Теорема 1.1. Через пряму і точку, що не лежить на ній, можна провести площину, і до того ж тільки одну.

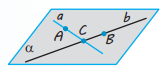Теорема 1.2. Через дві прямі, що перетинаються, можна провести площину, і до того ж тільки одну.

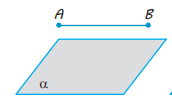Теорема 1.3. Площина розбиває простір на два півпростори. Якщо точки A і B належать одному півпростору, то відрізок AB не перетинає площину . Якщо ж точки A і B належать різним півпросторам, то відрізок AB перетинає площину.

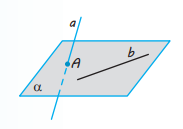Теорема 4.1. Якщо одна пряма лежить у даній площині, а друга пряма перетинає цю площину в точці, яка не належить першій прямій, то ці прямі мимобіжні.

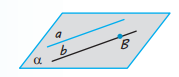
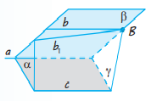Теорема 4.2. Через точку в просторі, яка не лежить на даній прямій, можна провести пряму, паралельну даній, і до того ж тільки одну.

Теорема 4.3. Дві прямі, які паралельні третій прямій, паралельні.

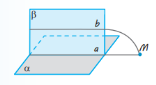Теорема 5.1 (ознака паралельності прямої та площини). Якщо пряма, яка не лежить у площині, паралельна якій-небудь прямій цієї площини, то вона паралельна і самій площині.

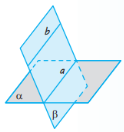
Теорема 5.2 (ознака паралельності двох прямих у просторі). Якщо площина проходить через пряму, паралельну іншій площині, і перетинає цю площину, то пряма їх перетину паралельна даній прямій.

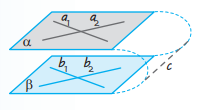
Теорема 6.1 (ознака паралельності двох площин). Якщо дві прямі, що перетинаються, однієї площини відповідно паралельні двом прямим другої площини, то ці площини паралельні.

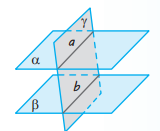
Теорема 6.2 (властивість паралельних площин). Якщо дві паралельні площини перетинаються третьою, то прямі перетину паралельні.

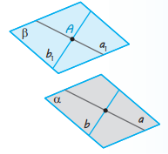
Теорема 6.3. Через точку поза даною площиною можна провести площину, паралельну даній, і до того ж тільки одну.

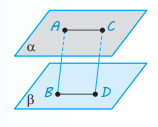
Теорема 6.4. Відрізки паралельних прямих, які містяться між двома паралельними площинами, рівні.