Правильні многокутники

Урок № 38

Тема уроку. Правильні многокутники.
Мета уроку: формування поняття правильного многокутника, центра і центрального кута правильного многокутника. Формування вмінь застосовувати вивчений матеріал до розв’язування задач.

Тип уроку: комбінований.

Хід уроку

І. Перевірка домашнього завдання

Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів під час виконання домашніх завдань.
II. Аналіз результатів тематичної контрольної роботи.
III. Повторення й узагальнення знань учнів про многокутники
Фронтальна бесіда
1. Сформулюйте означення многокутника; вершин многокутника; сторін многокутника; діагоналей многокутника.
2. Які многокутники вам відомі?
3. Скільки утворюється трикутників, якщо в n-кутнику (n > 3) провести всі його діагоналі з однієї вершини?
4. Що таке кут многокутника? зовнішній кут многокутника?
5. Чому дорівнює сума кутів опуклого n-кутника?
6. Чому дорівнює сума зовнішніх кутів опуклого многокутника?
7. В опуклого многокутника всі зовнішні кути прямі. Який це многокутник?
8. Чи можна побудувати чотирикутник з двома прямими і двома тупими кутами?
9. Чи може найменший кут чотирикутника становити 91°?
10. Чи можна побудувати опуклий п’ятикутник, усі кути якого прямі? Відповідь поясніть.
IV. Поетапне сприймання й усвідомлення нового матеріалу
Означення правильного многокутника
Серед розмаїття опуклих многокутників виділяють многокутники, у яких усі сторони рівні й усі кути рівні. Такі многокутники називають правильними.
Завдання класу:
1) Який трикутник є правильним?
2) Який чотирикутник є правильним?
3) Знайдіть кути правильного шестикутника.
4) Скільки сторін має правильний многокутник, зовнішній кут
якого становить 18°?
5) Знайдіть градусну міру кута правильного n-кутника.
6) Знайдіть градусну міру зовнішнього кута правильного n-кутника.
7) Скільки сторін має правильний многокутник, якщо кут при
його вершині дорівнює 108°?
Повторення відомостей про вписані й описані трикутники
Фронтальна бесіда
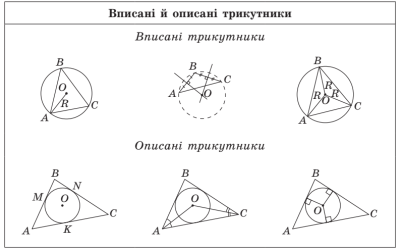
Запитання до класу з використанням табл. 4.
1) Яке коло називається описаним навколо трикутника? Що
можна сказати про такий трикутник (по відношенню до кола)?
2) Чи можна описати коло навколо будь-якого трикутника?
3) Де міститься центр кола, описаного навколо трикутника?
4) Яке коло називається вписаним у трикутник? Що можна сказати про такий трикутник (по відношенню до кола)?
5) Чи можна вписати коло в будь-який трикутник?
6) Де міститься центр кола, вписаного в трикутник?

Означення вписаних і описаних многокутників
Многокутник називається вписаним у коло, якщо всі його вершини лежать на цьому колі.
Многокутник називається описаним навколо кола, якщо всі його сторони дотикаються до цього кола.
Запитання до класу:
1) Де міститься центр кола, описаного навколо многокутника?
Чому?
2) Чи завжди можна описати коло навколо даного многокутника?
3) Побудуйте прямокутник та опишіть коло навколо нього.
4) Де міститься центр кола, вписаного в многокутник? Чому?
5) Чи завжди можна вписати коло в даний многокутник?
6) Побудуйте ромб та впишіть у нього коло.
7) Побудуйте правильний чотирикутник. Впишіть в нього коло й опишіть коло навколо нього.
Вивчення теореми
Теорема. Правильний многокутник є вписаним у коло й описаним навколо кола.

Доведення: (учні опрацьовують самостійно вдома)
Запитання до класу:
1. Чому бісектриси кутів A і B перетинаються?
2. α — кут многокутника. Чому дорівнюють кути OAB і OBA?
3. Визначте вид трикутника AOB. Обґрунтуйте відповідь.
4. Чому ΔABO = ΔВOC, ΔBOC = ΔСOD?
5. Чому OA = OB = OC = OD ? Який висновок можна зробити з цієї рівності?
6. Чому висоти трикутників AOB, BOC, COD, проведені з точки O, рівні?
7. Як буде розташовуватися коло з центром у точці O і радіусом, що дорівнює висоті трикутника, по відношенню до многокутника? Чому?
Слід зазначити, що з цієї теореми можна сформулювати такі
наслідки:
1) Усі бісектриси кутів правильного многокутника перетинаються в одній точці, яка є центром описаного кола.
2) Усі серединні перпендикуляри, проведені до сторін правильного многокутника, перетинаються в одній точці, яка є центром вписаного кола.
3) Центри вписаного й описаного кіл у правильному многокутнику збігаються.
4) Відрізок, що сполучає центр правильного многокутника з серединою сторони многокутника, є радіусом вписаного кола. Цей відрізок називається апофемою правильного многокутника.
Означення центрального кута правильного многокутника
Кут, під яким видно сторону правильного многокутника
з його центра, називається центральним кутом многокутника.
Завдання класу:
1) Чому дорівнює центральний кут правильного трикутника?
2) Чому дорівнює центральний кут правильного чотирикутника?
3) Чому дорівнює центральний кут правильного n-кутника?
4) Доведіть, що центральний кут правильного n-кутника дорівнює зовнішньому куту цього многокутника.

V. Закріплення й осмислення нового матеріалу
Виконання вправ:
1. Скільки сторін має правильний многокутник, кожний із внутрішніх кутів якого дорівнює 135°?
Розв’язання

Відповідь. 8 сторін.
2. Скільки сторін має правильний многокутник, якщо кожний із зовнішніх його кутів дорівнює 36°?
Розв’язання
Оскільки = 36, то 360 = 36n , n = 360 : 36, n = 10 .
Відповідь. 10 сторін.
 

VI. Домашнє завдання
1. Вивчити теоретичний матеріал.
2. Розв’язати задачі (на вибір учителя).
2) Скільки сторін має правильний многокутник, якщо кожний із зовнішніх його кутів дорівнює 24°?
VII. Підбиття підсумків уроку
запитання до класу
1. Який многокутник називається правильним?
2. Який многокутник називається вписаним у коло? описаним навколо кола?
3. Чи завжди можна вписати коло в правильний многокутник?
описати коло навколо правильного многокутника?
4. Що таке центр правильного многокутника? апофема?
5. Що таке центральний кут правильного многокутника? Чому
він дорівнює?