Презентація " Числові нерівності"
Про матеріал
Означення поняття “ більше”, “ менше”
Знаки нерівностей. Порівняння двох чисел.
Означення числової нерівності.
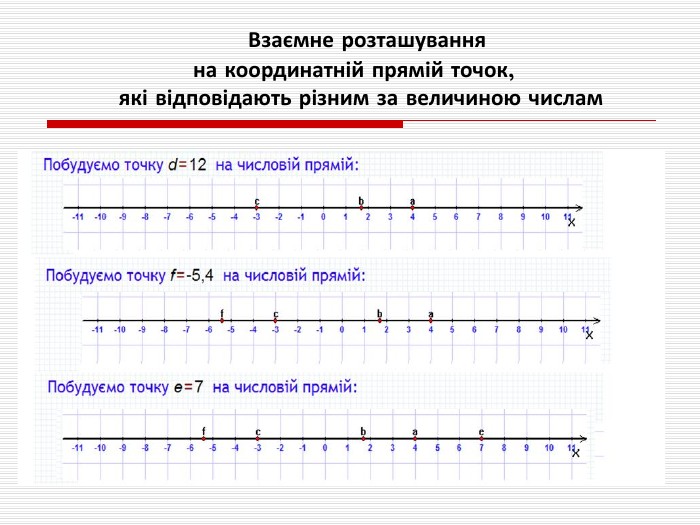
Взаємне розташування на координатній прямій точок, що відповідають різним за величиною числам.
Властивості числових нерівностей
Перегляд файлу
Зміст слайдів
ppt
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
1. Числові нерівності Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку