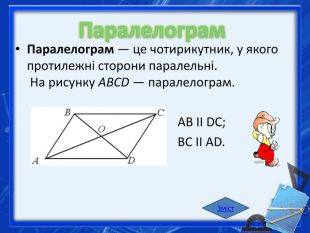
Презентація "Чотирикутники"

Вчитель. Білоус Юлія. Чотирикутники

Зміст. Означення Чотирикутники. Паралелограм Прямокутник. Ромб. Квадрат. Трапеція. Вписані і описані чотирикутники. Цікаві факти. Чотикикутники навколо нас Добірка задач

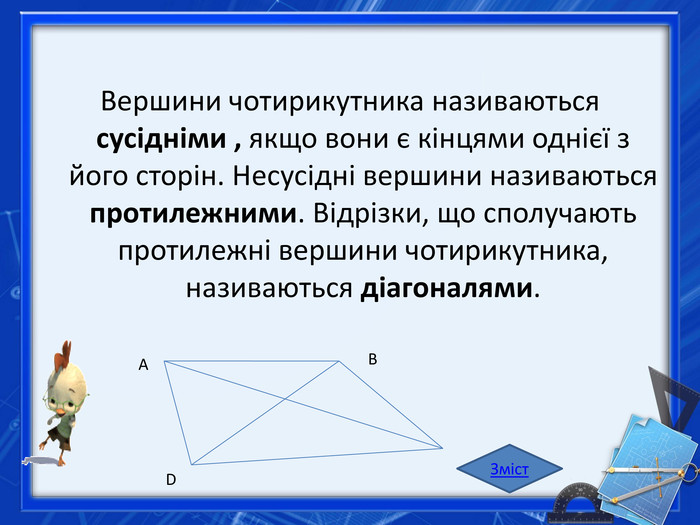
Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій, а відрізки, які їх сполучають, не повинні перетинатися. Дані точки називаються вершинами чотирикутника, а відрізки, що їх сполучають,— сторонами чотирикутника. Зміст

Вершини чотирикутника називаються сусідніми , якщо вони є кінцями однієї з його сторін. Несусідні вершини називаються протилежними. Відрізки, що сполучають протилежні вершини чотирикутника, називаються діагоналями. DВСAЗміст

A D В С Сторони чотирикутника, що виходять з однієї вершини, називаються сусідніми сторонами. Сторони, які не мають спільного кінця, називаються протилежними сторонами. Периметр чотирикутника — сума довжин усіх його сторін. P=(a+b)2, де a і b – сторони чотирикутника. Зміст

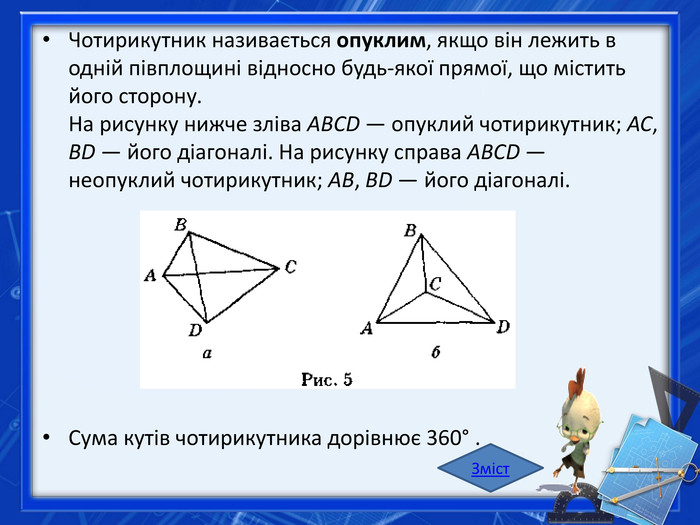
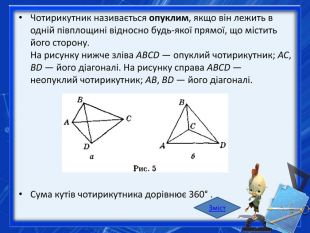
Чотирикутник називається опуклим, ­якщо він лежить в одній півплощині відносно будь-якої прямої, що містить його сторону. На рисунку нижче зліва ABCD — опуклий чотирикутник; AC, BD — його діагоналі. На рисунку справа ABCD — неопуклий чотирикутник; AB, BD — його діагоналі. Сума кутів чотирикутника дорівнює 360° . Зміст

Паралелограм — це чотирикутник, у якого протилежні сторони паралельні. На рисунку ABCD — паралелограм. AB ΙΙ DC; BC II AD. Зміст. Паралелограм

Теорема 1. У паралелограма протилежні сторони рівні, протилежні кути рівні. АВ=СD, BC=AD

Теорема 4. Діагональ паралелограма поділяє його на два рівні трикутники. На рисунку нижче зліва ABC = CDAНа рисунку справа ABD = CDB Зміст. Властивості паралелограма

Властивості паралелограма. Теорема 5. Діагоналі паралелограма розбивають його на дві пари рівних трикутників. На рисунку AOB = COD, BOC = DOA Зміст

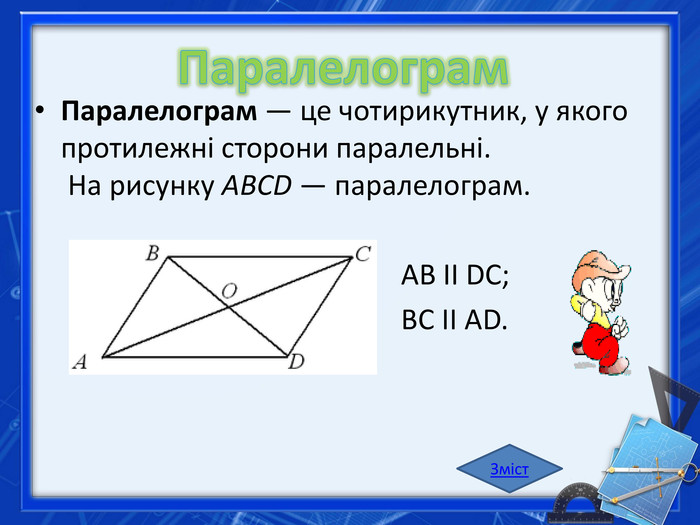
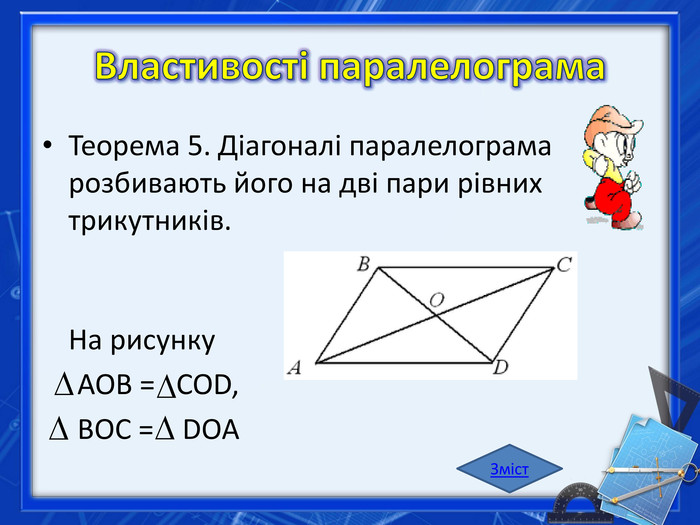
Теорема 1. Якщо діагоналі чотирикутника перетинаються й у точці перетину діляться навпіл, то цей чотирикутник — паралелограм. Теорема 2. Якщо в чотирикутнику дві сторони паралельні й рівні, то цей чотирикутник — паралелограм. Теорема 3. Якщо в чотирикутнику протилежні сторони рівні, то цей чотирикутник — паралелограм. Теорема 4. Якщо в чотирикутнику протилежні кути рівні, то цей чотирикутник — паралелограм. Теорема 5. Якщо в чотирикутнику кути, що є прилеглими до кожної із сторін, у сумі дорівнюють , то цей чотирикутник — паралелограм. Теорема 6. Якщо кожна діагональ поділяє чотирикутник на два рівні трикутники, то цей чотирикутник — паралелограм. Зміст. Ознаки паралелограма

Висота паралелограма — це відрізок, перпендикулярний до протилежних сторін паралелограма з кінцями на цих сторонах. На рисунку h₁ I h₂— висоти паралелограмa. Зміст. Кут між висотами паралелограма

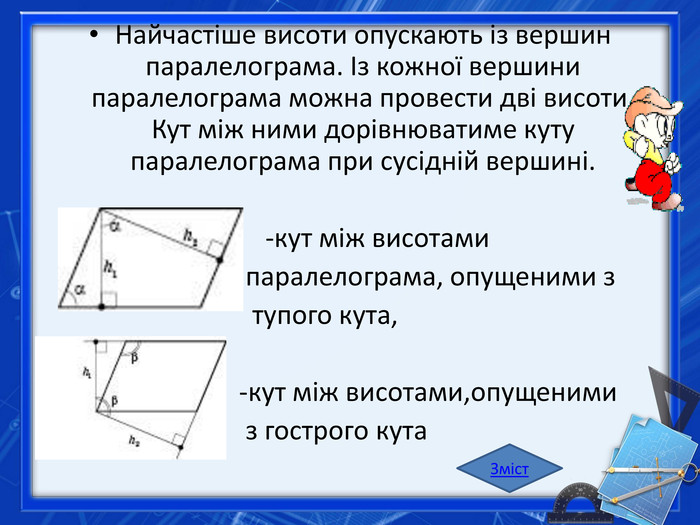
Найчастіше висоти опускають із вершин паралелограма. Із кожної вершини паралелограма можна провести дві висоти. Кут між ними дорівнюватиме куту паралелограма при сусідній вершині. -кут між висотами паралелограма, опущеними з тупого кута, -кут між висотами,опущеними з гострого кута. Зміст

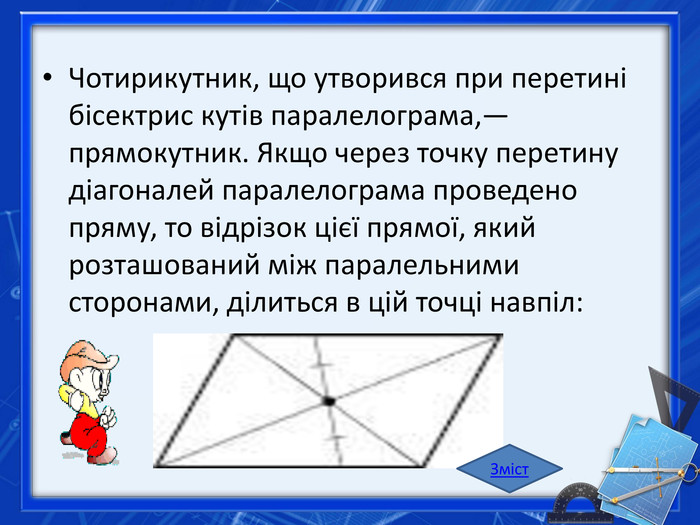
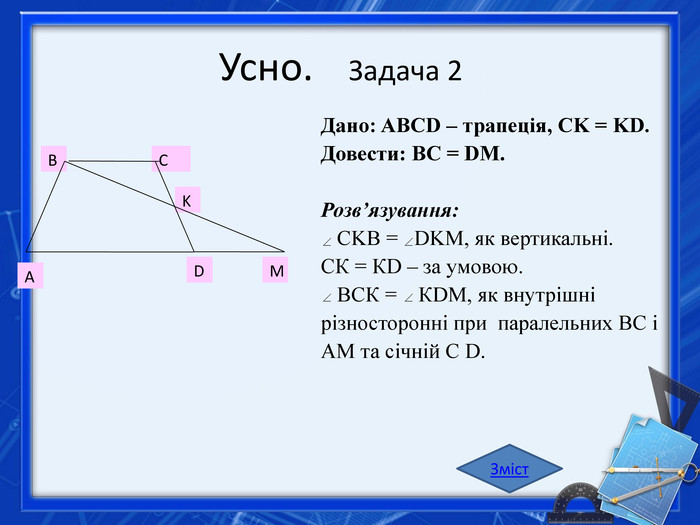
Властивості бісектрис кутів паралелограма1. Бісектриси сусідніх кутів паралелограма перпендикулярні.2. Бісектриси протилежних кутів паралелограма паралельні або збігаються (якщо паралелограм — ромб).3. Бісектриса кута паралелограма відокремлює від нього рівнобедрений трикутник. На рисунку BM II KD; DM II AP; - рівнобедрений; AB=BP; KCD - рівнобедрений, CK=CD . Зміст

Чотирикутник, що утворився при перетині бісектрис кутів паралелограма,— прямокутник. Якщо через точку перетину діагоналей паралелограма проведено пряму, то відрізок цієї прямої, який розташований між паралельними сторонами, ділиться в цій точці навпіл: Зміст

Прямокутник — це паралелограм, у якого всі кути прямі. Зміст. Прямокутник

Оскільки прямокутник є паралелограмом, він має всі властивості паралелограма і ще деякі інші. Теорема. Діагоналі прямокутника рівні. На рисунку AO=OC=BO=OD. AC=BD . AOB= COD ; BOC= DOA — рівнобедрені. Зміст

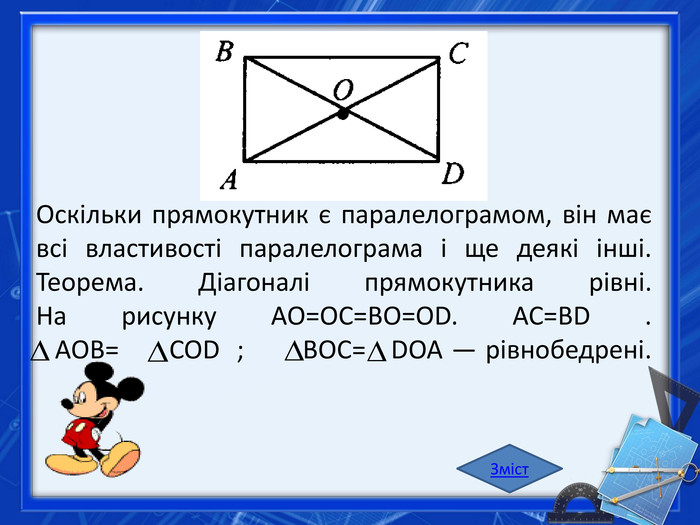
Теорема 1. Якщо в чотирикутнику всі кути рівні, то він є прямокутником. Теорема 2. Якщо в чотирикутнику є три прямі кути, то він є прямокутником. Теорема 3. Якщо в паралелограмі є прямий кут, то паралелограм є прямокутником. Теорема 4. Якщо в паралелограмі діагоналі рівні, то він є прямокутником. Зміст. Ознаки прямокутника

Ромб — це паралелограм, у якого всі сторони рівні. Зміст. Ромб

Оскільки ромб є паралелограмом, він має всі властивості паралелограма і деякі інші. Теорема 1. Діагоналі ромба перетинаються під прямим кутом. Діагоналі ромба є бісектрисами його кутів. На рисунку ABCD — ромб;AB=BC=CD=DA; AC BD;

Властивості ромба Теорема 2. Діагоналі ромба розбивають його на чотири рівні прямокутні трикутники. Теорема 3. Висоти ромба рівні: Зміст

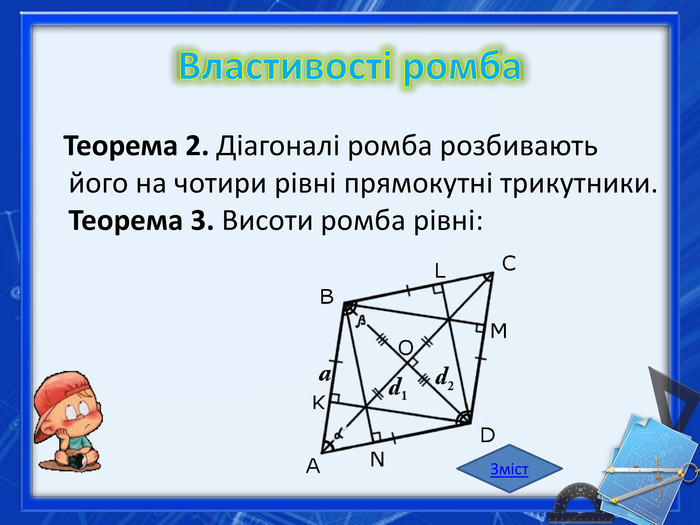
Ознаки ромба Теорема 1. Якщо в чотирикутнику всі сторони рівні, то він є ромбом. Теорема 2. Якщо в паралелограмі сусідні сторони рівні, то він є ромбом. Теорема 3. Якщо в паралелограмі діагоналі перпендикулярні, то він є ромбом. Теорема 4. Якщо в паралелограмі діагональ є бісектрисою кута, то паралелограм є ромбом. Зміст

Квадрат Квадрат — це прямокутник, у якого всі сторони рівні. A B D CЗміст

Властивості квадрата Оскільки квадрат є паралелограмом, прямокутником і ромбом водночас, маємо:1) у квадрата всі сторони рівні;2) у квадрата всі кути рівні;3) діагоналі квадрата рівні, перетинаються під прямим кутом, діляться в точці перетину навпіл, є бісектрисами його кутів;Зміст

Властивості квадрата 4) діагоналі квадрата ділять його на чотири рівні рівнобедрені прямокутні трикут­ники. На рисунку ABCD — квадрат. AB = BC =CD=AD;

Ознаки квадрата Теорема 1. Якщо в чотирикутника всі сторони і всі кути рівні, то він є квадратом. Теорема 2. Якщо діагоналі прямокутника перетинаються під прямим кутом, то він є квадратом. Теорема 3. Якщо діагоналі ромба рівні, то він є квадратом. Зміст

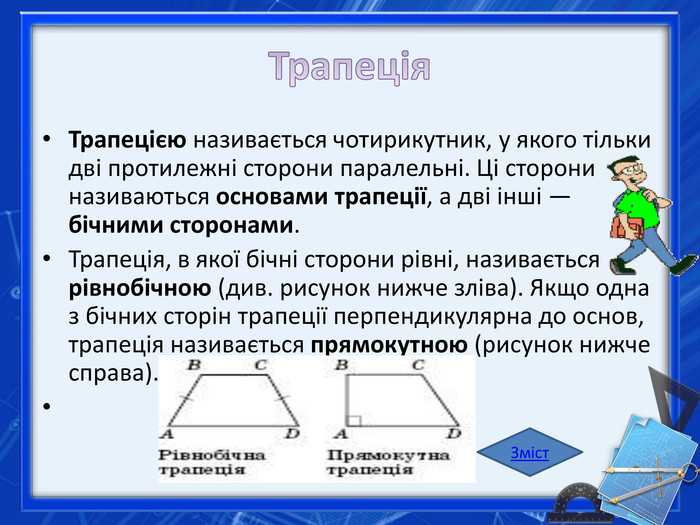
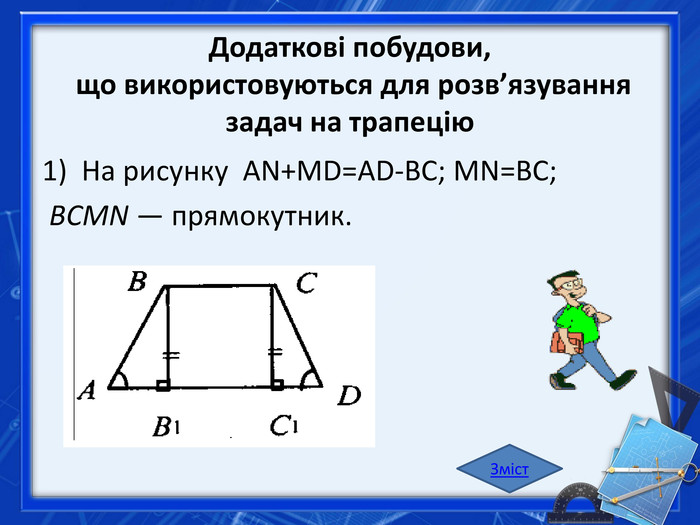
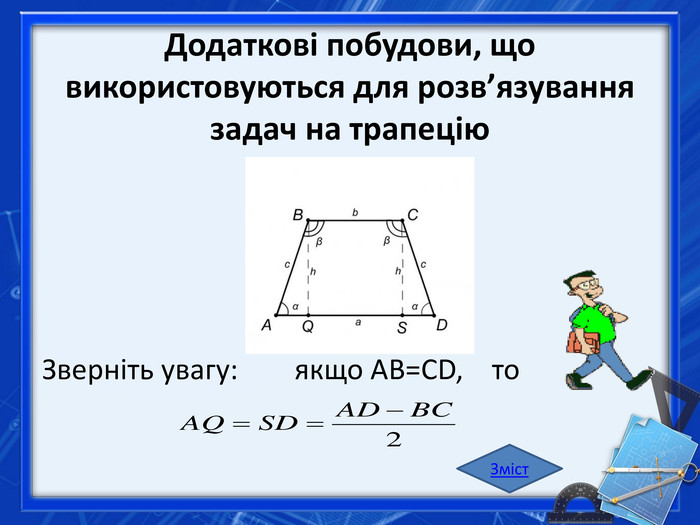
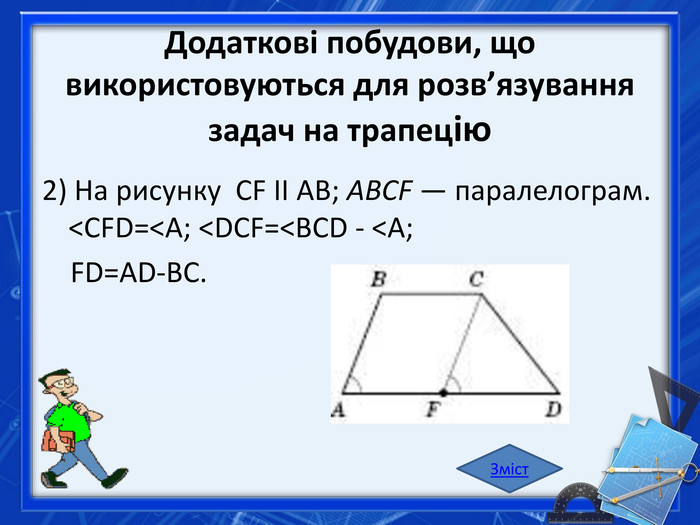
Трапеція. Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні. Ці сторони називаються основами трапеції, а дві інші — бічними сторонами. Трапеція, в якої бічні сторони рівні, називається рівнобічною (див. рисунок нижче зліва). Якщо одна з бічних сторін трапеції перпендикулярна до основ, трапеція називається прямокутною (рисунок нижче справа). Зміст

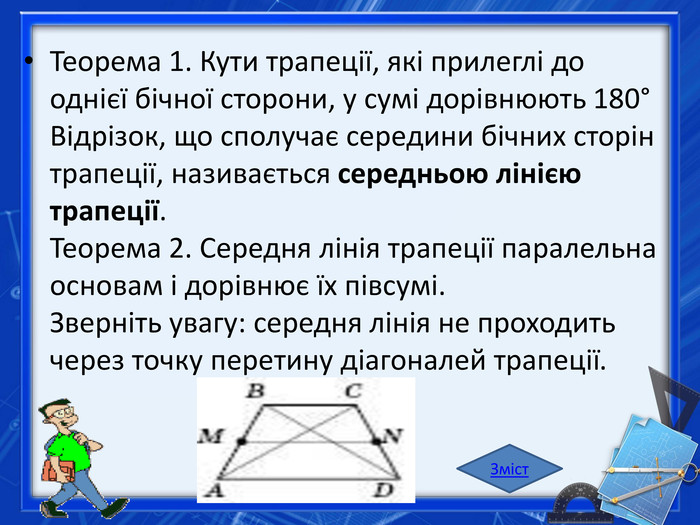
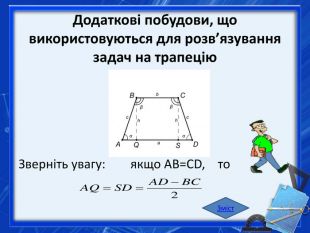
Теорема 1. Кути трапеції, які прилеглі до однієї бічної сторони, у сумі дорівнюють 180° Відрізок, що сполучає середини бічних сторін трапеції, називається середньою лінією трапеції. Теорема 2. Середня лінія трапеції паралельна основам і дорівнює їх півсумі. Зверніть увагу: середня лінія не проходить через точку перетину діагоналей трапеції. Зміст

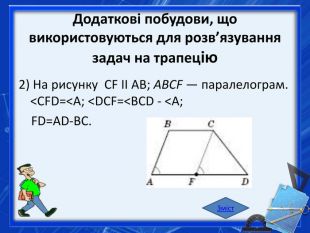
Рисунок 1 Висотою трапеції називається відрізок прямої, перпендикулярної до основ трапеції з кінцями на основах трапеції. Найчастіше висоту проводять через вершини верхньої основи або через точку перетину діагоналей (рисунок 1). Усі висоти трапеції рівні між собою. Бісектриса кута трапеції, якщо вона перетинає основу трапеції, відтинає від неї рівнобедрений трикутник (рисунок 2). Рисунок 2 Зміст

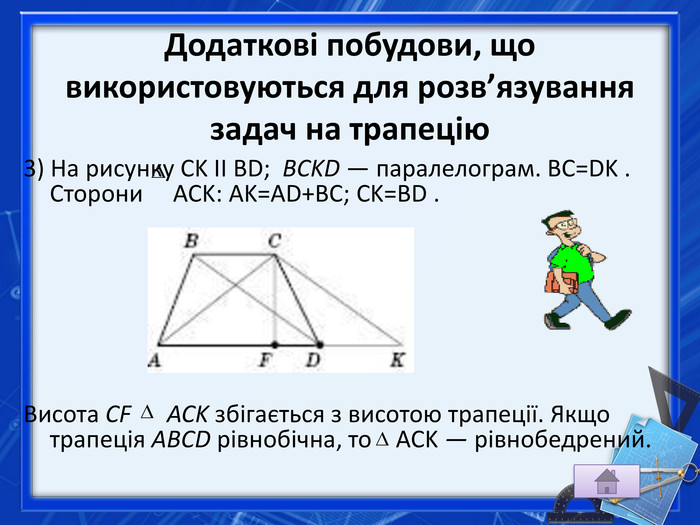
Властивості рівнобічної трапеції1. У рівнобічній трапеції кути при основах рівні (рисунок нижче зліва).2. У рівнобічній трапеції діагоналі рівні.3. У рівнобічній трапеції діагоналі створюють з основою рівні кути.4. У рівнобічній трапеції діагоналі, перетинаючись, утворюють два рівнобедрені трикутники, основами яких є основи трапеції (рисунок справа). Зміст

Додаткові побудови, що використовуються для розв’язування задач на трапецію. На рисунку AN+MD=AD-BC; MN=BC; BCMN — прямокутник. Зміст

Додаткові побудови, що використовуються для розв’язування задач на трапецію. Зверніть увагу: якщо AB=CD, то Зміст

Додаткові побудови, що використовуються для розв’язування задач на трапецію2) На рисунку CF II AB; ABCF — паралелограм.

Додаткові побудови, що використовуються для розв’язування задач на трапецію3) На рисунку CK II BD; BCKD — паралелограм. BC=DK . Сторони ACK: AK=AD+BC; CK=BD . Висота CF ACK збігається з висотою трапеції. Якщо трапеція ABCD рівнобічна, то ACK — рівнобедрений.

Вписані й описані чотирикутники. Теорема 1. Навколо чотирикутника можна описати коло тоді й тільки тоді, коли сума його протилежних кутів дорівнює 180° . На рисунку . Зміст

Із цього випливає, що коло можна описати навколо прямокутника (рисунок нижче зліва), зокрема квадрата (рисунок справа), його центром буде точка перетину його діагоналей. Радіус — половина діагоналі. Зміст

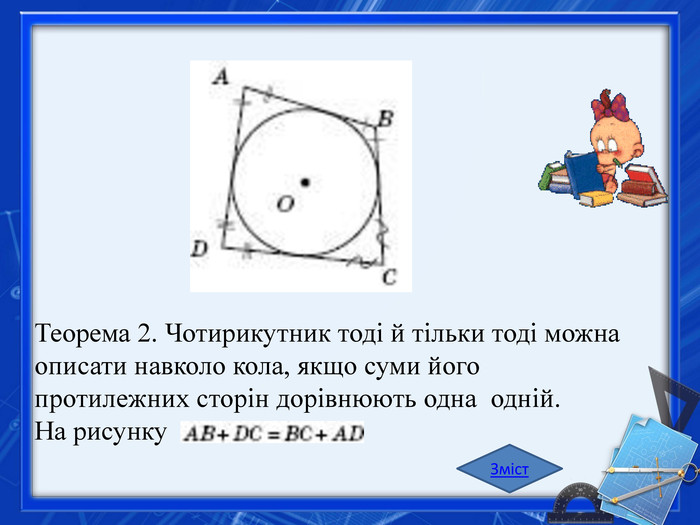
Коло можна описати навколо трапеції тоді й тільки тоді, коли вона є рівнобічною (див. рисунок). Центром кола є точка перетину середніх перпендикулярів до сторін. Навколо паралелограма та трапеції загального виду описати коло не можна. (Зокрема, навколо ромба не можна описати коло.)Зміст

Теорема 2. Чотирикутник тоді й тільки тоді можна описати навколо кола, якщо суми його протилежних сторін дорівнюють одна ­ одній. На рисунку Зміст

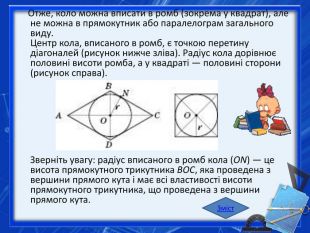
Отже, коло можна вписати в ромб (зокрема у квадрат), але не можна в прямокутник або паралелограм загального виду. Центр кола, вписаного в ромб, є точкою перетину діагоналей (рисунок нижче зліва). Радіус кола дорівнює половині висоти ромба, а у квадраті — половині сторони (рисунок справа). Зверніть увагу: радіус вписаного в ромб кола (ON) — це висота прямокутного трикутника BOC, яка проведена з вершини прямого кута і має всі властивості висоти прямокутного трикутника, що проведена з вершини прямого кута. Зміст

Теорема 3. Трапецію тоді й тільки тоді можна описати навколо кола, коли сума її основ дорівнює сумі бічних сторін (рисунок нижче зліва). Центр цього кола — точка перетину бісектрис кутів трапеції. Радіус дорівнює половині висоти трапеції. У випадку рівнобічної трапеції центр вписаного кола лежить на середині висоти трапеції, яка проходить через середини основ (рисунок справа). Бічна сторона трапеції у цьому випадку дорівнює її середній лінії. Зміст

Цікаві факти- у Китаї ростуть дерева висотою 3-5м , що мають квадратний зріз стовбура; у США виростили сорт кукурудзи, зерна якої мають квадратну форму, вони не скочуються з тарілок під час вживання їжі в літаках. Леонардо да Вінчі (1452-1519) довів , що тіло людини вписується в квадрат. Зміст

Чотирикутники навколо нас. Мистецтво Зміст

Будівництво. Зміст

Повсякденне життя. Зміст

Добірка задач Усно. Задача 1 Дано: ABCD – рівнобічна трапеція. Довести: A = D . Розв’язування: AB = CD за умовою. CK = AB за побудовою, бо ABCK – паралелограм. Отже, CK = CD та D = CKD. Але A та CKD відповідні кути при AB//CK та січній AK. Отже, A = D. С BAKDЗміст

KBCУсно. Задача 2 Дано: ABCD – трапеція, CK = KD. Довести: BC = DM. Розв’язування: CKB = DKM, як вертикальні. СК = КD – за умовою. ВСК = КDМ, як внутрішні різносторонні при паралельних ВС і АМ та січній С D. ADМЗміст

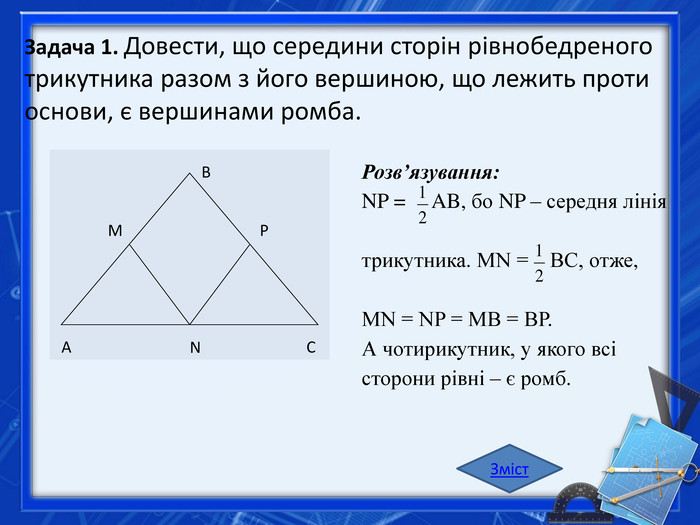
Задача 1. Довести, що середини сторін рівнобедреного трикутника разом з його вершиною, що лежить проти основи, є вершинами ромба. Розв’язування: NP = AB, бо NP – середня лінія трикутника. МN = BС, отже, МN = NP = МВ = ВР. А чотирикутник, у якого всі сторони рівні – є ромб. АВМРСNЗміст

Задача 2. У паралелограмі ABCD протилежні сторони BC і AD розділені точками L та M відповідно пополам і ці точки з’єднані відрізками з кінцями сторін AD і BC. Довести, що утворений при перетині проведених відрізків чотирикутник – паралелограм. Розв’язування: LC//AM та LC = AM – за умовою. За відповідністю чотирикутник, у якого дві сторони рівні й паралельні – паралелограм. LCMA – паралелог- рам. Отже, LK//MP. Аналогічно, LP//КM. Чотирикутник, у якого сторони лежать на паралельних прямих, паралелограм. АВLCDMKPЗміст

МNЗадача 3. Навколо кола описана рівнобічна трапеція, основи якої відносяться, як 2:3, а середня лінія 10 см. Знайти всі сторони трапеції. Ми говорили, що в трапецію можна вписати коло, сума бічних сторін дорівнює сумі її основ. Розв’язування: АВ + СD =ВС + АD. Нехай ВС = 2х см, АД =3х см. За теоремою про середню лінію трапеції: 10 см, 5х = 20, х = 4. ВС = 2*4= 8 см, АD= 3*4= 12 см,АDОBCЗміст

CВАDKccda-b. Задача 4. Побудувати трапецію за основами і бічними сторонами. Розв’язування: Будуємо за трьома сторонами. Проведемо пряму та . Доведення: та (як протилежні сторони паралелограма). Трапецію – побудовано. А1 D1 K1 C1 В1ccda-b

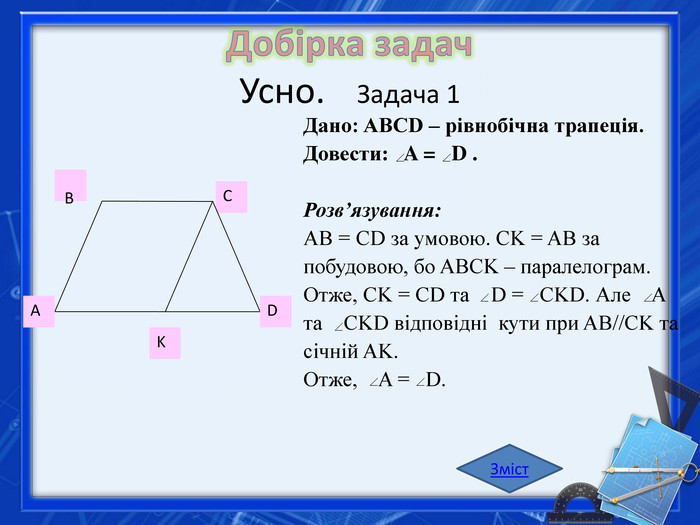
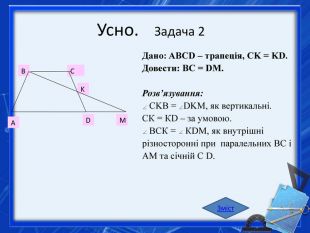
Дано: ABCD – трапеція, AB=BC=CD, AC CD. Знайти: A, B, C, D. Розв’язування: BAC = BCA, як кути при основі рівнобедреного трикутника ABC. BCA = CAD, як внутрішнірізносторонні при паралельних BC і AD та січній AC. Отже, BAC = CAD= x°, A = D= 2x°. CAD + D = 90°. ABCDОтже, x°+2 x°=90°, x=30°. А=2*30°=60°. D=60°, B=180° - 60°=120°. А і В – внутрішні односторонні кути. С= 90° + 30°=120°. Зміст

Дано: ABCD – трапеція, MN – середня лінія, MN = 7см, AD – BC = 4 см. Знайти: основи трапеції. Розв’язування: BC = х см, тоді AD = (х + 4) см. За теоремою про середню лінію трапеції: (см). BC = 5 см, AD = 9 см. AМВСNDЗміст

До нових зустрічей! Дякую за увагу!