Презентація "Цікавинки для обдарованих математиків"

Презентацію склав. Учитель математики Піщанського НВКЧернишов В. М. ЦІКАВИНКИ ДЛЯ ОБДАРОВАНИХ МАТЕМАТИКІВ

ОЗНАКИ ПОДІЛЬНОСТІ ЧИСЕЛВ ШКІЛЬНОМУ КУРСІ МАТЕМАТИКИ ВИВЧАЮТЬСЯ ТАКІ ОЗНАКИ ПОДІЛЬНОСТІ ЧИСЕЛ

Приклад 3 Чи ділиться число 52 на 4?5+2/2 = 6, число парне, значить, число на 4 ділиться. Приклад 4 Чи ділиться число 134 на 4?13+4/2 = 15, число непарне, значить, 134 на 4 не ділиться. На 4 число ділиться, якщо дві останні цифри числа діляться на 4. Приклад : Число 23764 Дві останніх цифри (64) діляться на 4, значить і само число ділиться на 4 Удосконалена ознака подільності числа на 4 Якщо половина числа одиниць в сумі з числом десятків – парне число, то число ділиться на 4.

Щоб взнати, чи ділиться трьохцифрове число на 8, можна половину його одиниць додати до десятків. У отриманого числа так само — половину одиниць додати до десятків. Якщо отримана сума ділиться на 2, значить, число ділиться на 8. Наприклад, 952: 95 + 1 = 96, далі 9 + 3 = 12. Значить, 952 ділиться на 8. На 8 число ділиться, якщо три останні цифри числа діляться на 8. Приклад : Число 23764 Три останніх цифри (764) діляться на 8, значить і само число ділиться на 8

Число ділиться на 7 тоді и тільки тоді, коли результат віднімання подвоєної останньої цифри з цього числа без останньої цифри ділиться на 7 (наприклад, 364 ділиться на 7, тому,що 36 – (2 × 4) = 28 ділиться на 7). Для того, щоб натуральне число ділилося на 7 необхідно и достатньо, щоб алгебраїчна сума чисел, які утворюють непарні групи по три цифри (починаючи з одиниць) взятих зі знаком «+» и парних зі знаком «-» ділилася на 7 (наприклад, число 689255. Перша група зі знаком «+» (689), друга зі знаком «-» (255). Значить 689 – 255 = 434. В свою чергу 434 : 7 = 62). Удосконалена ознака подільності числа на 7 Щоб перевірити, чи ділиться число на 7, треба від числа відкинути останню цифру і від результату цю цифру двічі відняти. Якщо результат ділиться на 7, то і саме число ділиться на 7. Приклад 1: Чи ділиться на 7 число 238? 23 – 8 – 8 = 7. Значить, число 238 ділиться на 7. Дійсно, 238 = 34х7. Цю дію можна проводити багаторазово. Приклад 2: Чи ділиться на 7 число 65835?6583 – 5 – 5 = 6573; 657 – 3 – 3 = 651; 65 – 1 – 1 = 63.63 ділиться на 7. Значить, і число 65835 ділиться на 7.

Треба взяти останню цифру числа, і відняти її із «числа, яке залишилося без останньої цифри». Потім знову перевірити, якщо те, що вийшло , ділиться на 11, то й само число ділиться на 11. Якщо різниця між сумою цифр числа, які стоять на непарних місцях, і сумою цифр, які стоять на парних місцях дорівнює нулю або ділиться на 11, то і само число ділиться на 11. Приклад: Чи ділиться число 8347823 на 11? Знайдемо суму цифр на непарних місцях 3 + 8 + 4+ 8 = 23, сума цифр на парних місцях 2 + 7 + 3 = 12. Різниця сум буде 23 – 12 = 11. 11 ділиться на 11, значить і число 8347823 ділиться на 11. 8347823 : 11= 758893

Ознака подільності на 13 Треба взяти останню цифру числа, і помножити її на 4, додати до числа, яке залишилося без останньої цифри. Потім знову перевірити, якщо те, що отримали, ділиться на 13, то і само число ділиться на 13. Приклад: Чи ділиться на 13 число 845?За ознакою маємо: 84 + (4 × 5) = 104, 10 + (4 × 4) = 26, 26 ділиться на 13, а значить і 845 ділиться на 13. Приклад: Чи ділиться на 13 число 65835? 6583+4 × 5 = 6603; 660+4 × 3 = 672; 67+4 × 2 = 79; 7+4 × 9 = 43. Число 43 не ділиться на 13, значить, і число 65835 не ділиться на 13. Приклад: Чи ділиться на 13 число 715?71+ 4 × 5 = 91; 9 + 4 × 1 = 1313 ділиться на 13, значить, і число 715 ділиться на 13.

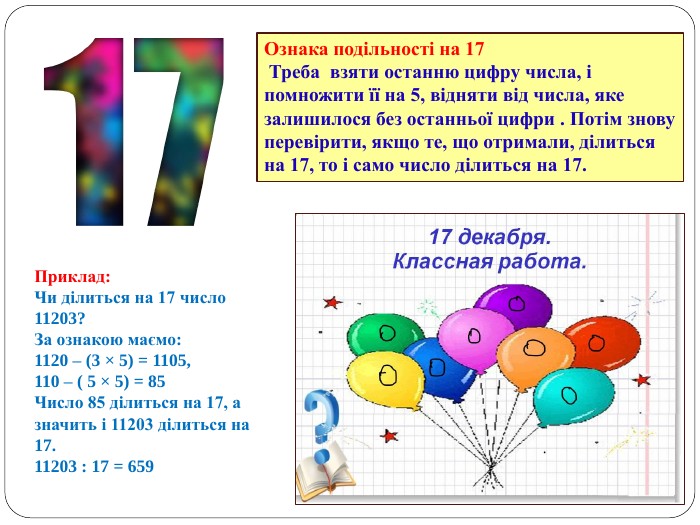
Ознака подільності на 17 Треба взяти останню цифру числа, і помножити її на 5, відняти від числа, яке залишилося без останньої цифри . Потім знову перевірити, якщо те, що отримали, ділиться на 17, то і само число ділиться на 17. Приклад: Чи ділиться на 17 число 11203?За ознакою маємо: 1120 – (3 × 5) = 1105, 110 – ( 5 × 5) = 85 Число 85 ділиться на 17, а значить і 11203 ділиться на 17.11203 : 17 = 659

Ознака подільності на 19 Треба взяти останню цифру числа, і помножити її на 2, додати до числа, яке залишилося без останньої цифри . Потім знову перевірити, якщо те, що отримали, ділиться на 19, то і само число ділиться на 19. Приклад: Чи ділиться на 19 число 646?За ознакою маємо: 64 + (6 × 2) = 76, 7 + ( 6 × 2) = 19. Число 19 ділиться на 19, а значить і 646 ділиться на 19. 646 : 19 = 34 Приклад: Чи ділиться на 19 число 148656?За ознакою маємо: 14865 + (6 ×2) = 14877, 1487 + (7 × 2) = 1501, 150 + (1 × 2) = 152, 15 + (2 × 2) = 19. Число 19 ділиться на 19, а значить і 148656 ділиться на 19.148656 : 19 = 7824.

Ознака подільності на 23 Число ділиться на 23 тоді і тільки тоді, коли число його сотень, складене з потроєним числом десятків і одиниць, кратне 23 Приклад: Чи ділиться число 28842 на 23?За ознакою маємо : 288 + (3 × 42) = 414; продовжуємо: 4 + (3 × 14) = 46 . Число 46 ділиться на 23, значить і число 28842 ділиться на 23.

Способи швидкого додавання і віднімання (для швидкого додавання і віднімання використовують «прийом округлення», який застосовують тоді, коли хоча б один із компонентів цих дій є числом, близьким до круглих десятків, сотень, тисяч, тощо.)1. Якщо один із доданків збільшити на декілька одиниць, то з отриманої суми треба відняти стільки ж одиниць            Приклади:274 + 97 = 274 + (97 + 3) - 3 = 274 + 100 – 3 = 374 – 3 = 371;1996 + 759 = (1996 + 4) – 4 + 759 = 2000 + 759 – 4 = 2759 – 4 = 2755. 2. Якщо один із доданків збільшити на кілька одиниць, а другий зменшити на стільки ж одиниць, то сума не зміниться. На підставі цього виконується округлення одного доданка за рахунок другого            Приклад:998 + 1526 = 1000 + 1524 = 2524.

3. Якщо від'ємник збільшити на кілька одиниць, то, щоб різниця не змінилася, треба і зменшуване збільшити на стільки ж одиниць      Приклад:5431 – 3996 = (5431 + 4) – (3996 + 4) = 5435 - 4000 = 1435.4. Якщо зменшуване зменшити на кілька одиниць, то до отриманої різниці треба додати стільки ж одиниць            Приклад:10013 – 9775 = (10013 – 13) – 9775 + 13 = 1000 – 9775 = 225 + 13 = 238

Приклади:167 · 9 = 1670 – 167 = 1503; 26 · 99 = 2600 – 26 = 2574. Приклади:615 · 98 = 615 · (100 – 2) = 615 · 100 – 615 · 2 = 61500 – 1210 = 60290;5015 · 1002 = 5015 · (1000 + 2) = 5015 · 1000 + 5015 · 2 = 5015000 + 10030 = 5025030. СПОСОБИ ШВИДКОГО МНОЖЕННЯ І ДІЛЕННЯ1. Множення на 9, 99, 999 тощо. Щоб помножити будь-яке число на число, що записане дев'ятками, треба до першого множника приписати справа стільки нулів, скільки дев'яток у другому множнику, і з результату відняти перший множник            2. Множення на число, близьке до одиниці будь-якого разряду.            

3. Множення двозначного числа на 11. Щоб помножити двоцифрове число, сума цифр якого менше 10, на 11, треба між цифрами числа написати суму його цифр. Щоб помножити на 11 двоцифрове число, сума цифр якого більше або дорівнює 10, треба між цифрою десятків, збільшеної на 1, і цифрою одиниць написати різницю між сумою цифр числа і числом 10.                 Пример:86 · 11 = 946. Пример:63 · 11 = 693. Приклади:1246 · 5 = 6230, так как 1246 : 2 = 623;6428 · 25 = 160700, так как 6428 : 4 = 1607;8032 · 125 = 1004000, так как 8032 : 8 = 1004.4. Множення на 5, 25, 125. Щоб помножити число на 5, 25, 125, досить розділити його відповідно на 2, 4, 8 і помножити на 10, 100, 1000.   

Приклади:315 : 5 = 63, так как 315 · 2 = 630;2025 : 25 = 81, так как 2025 · 4 = 8100;10125 : 125 = 81, так как 10125 · 8 = 81000.5. Ділення чисел на 5, 25, 125. Щоб розділити число на 5, 25, 125, досить помножити його відповідно на 2, 4, 8 і розділити на 10, 100, 1000.   Приклад: Обчислити 352. Розв’язок (виконується усно). 3 · 4 = 12, дописавши справа 25, отримаємо результат: 352 = 1225.6. Піднесення до квадрату, в запису яких остання цифра 5. Щоб піднести до квадрату число, що закінчується цифрою 5, треба число його десятків помножити на число, збільшене на одиницю, і справа дописати 25.

Приклад: Обчислити 572. Розв’язок (виконується усно). До 25 додаємо 7, отримуємо 32 і дописуємо 49. Отримуємо результат: 572 = 3249. Аналогічно, 532 = 2809.7. Піднесення числа, яке має 5 десятків до квадрату. Щоб піднести до квадрату двоцифрове число, що має 5 десятків, треба до числа 25 додати число одиниць і до результату дописати справа квадрат числа одиниць так, щоб вийшло чотирицифрове число.