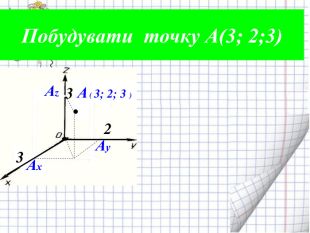
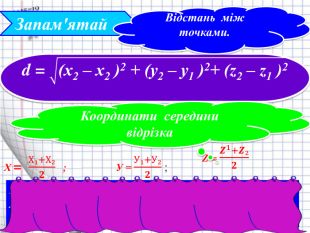
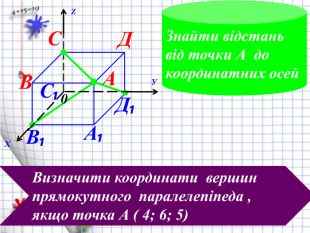
Презентація, " Декартові координати у просторі"
Про матеріал
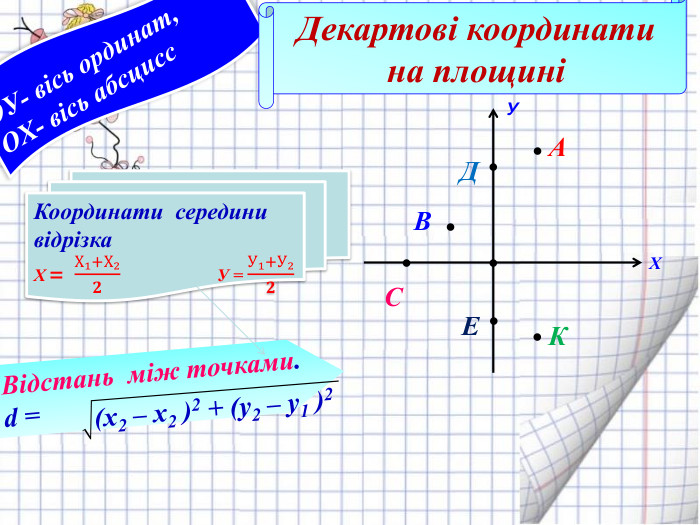
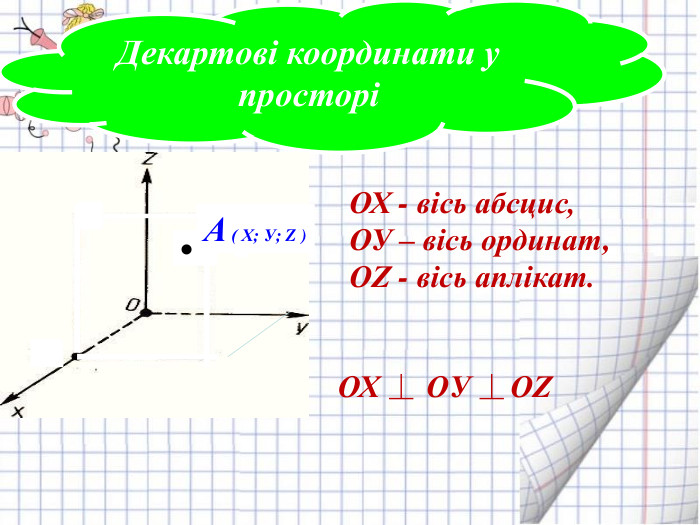
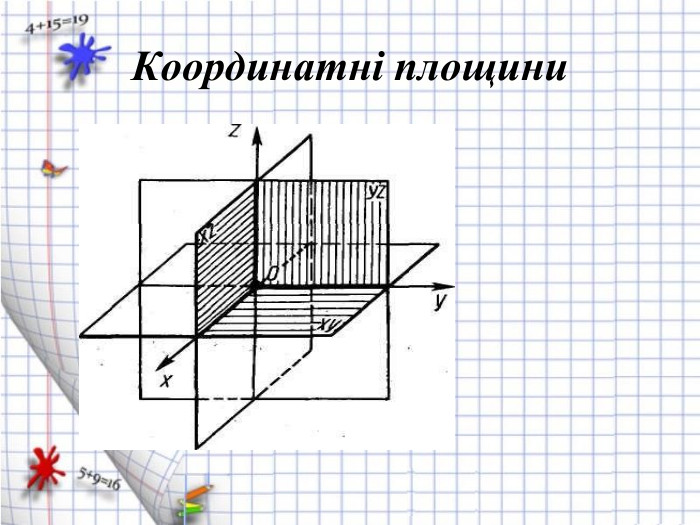
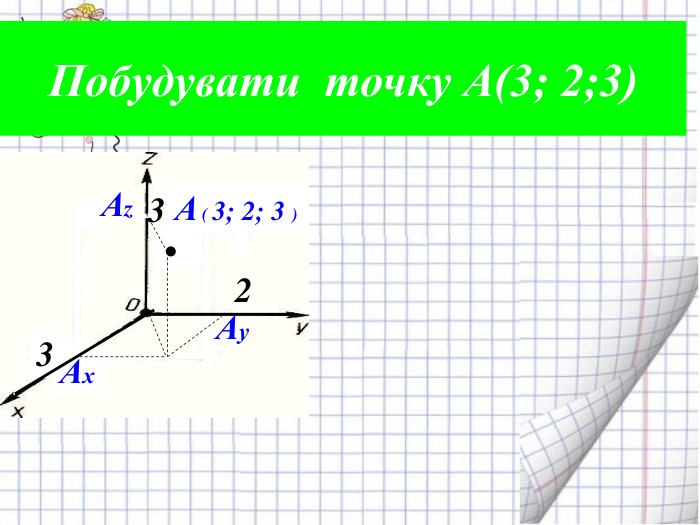
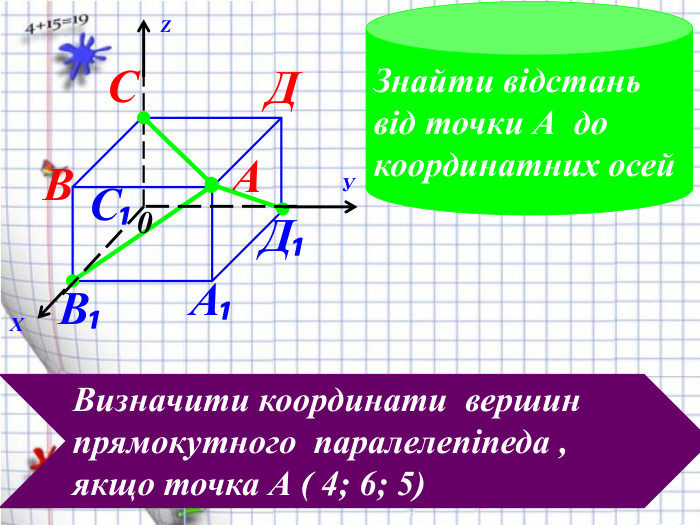
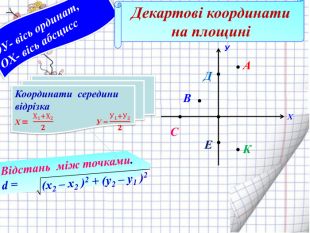
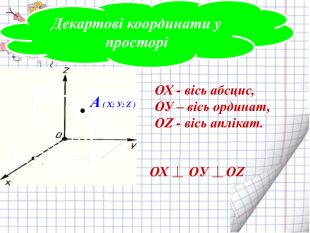
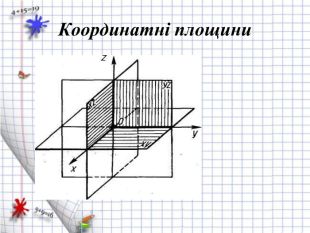
Ознайомити з декартовими координатами у просторі, формувати застосовувати формулу відстані між точками та координат середини відрізка до розв'язування задач Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку