Презентація "Декартові координати в просторі"
Про матеріал
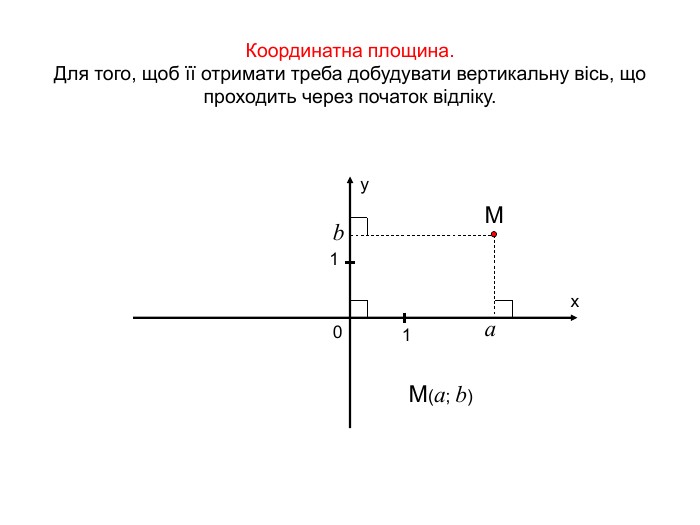
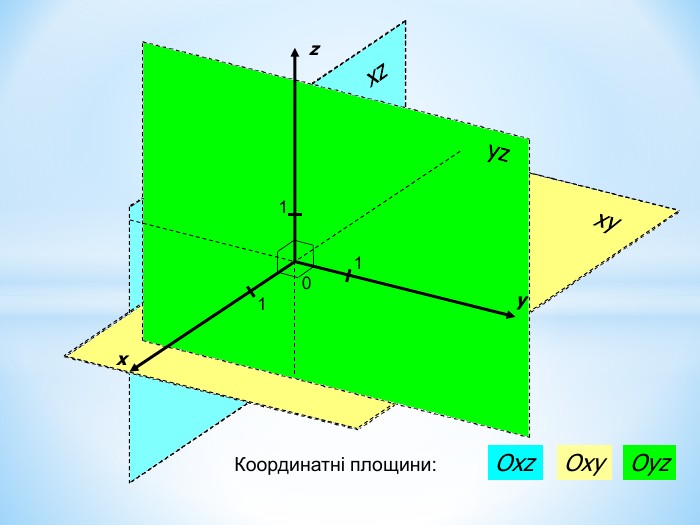
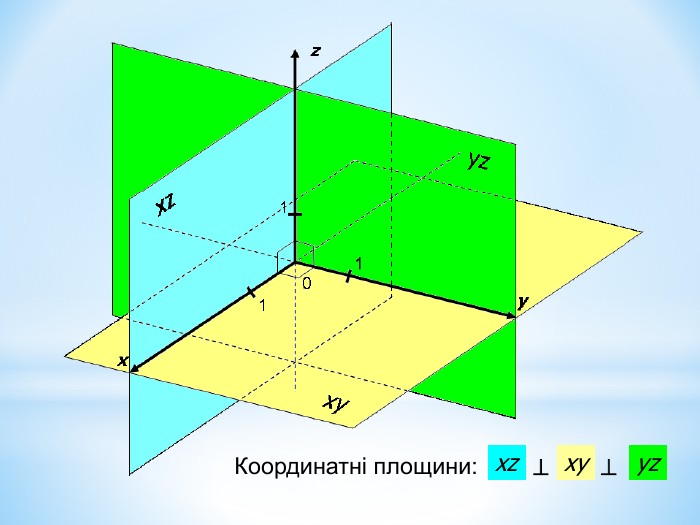
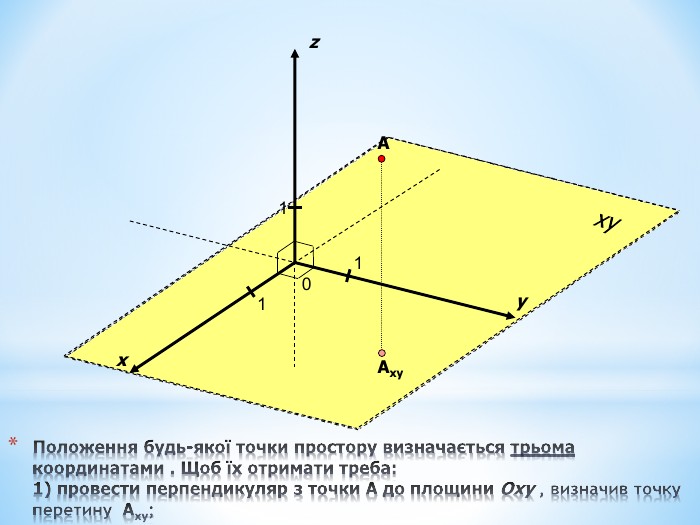
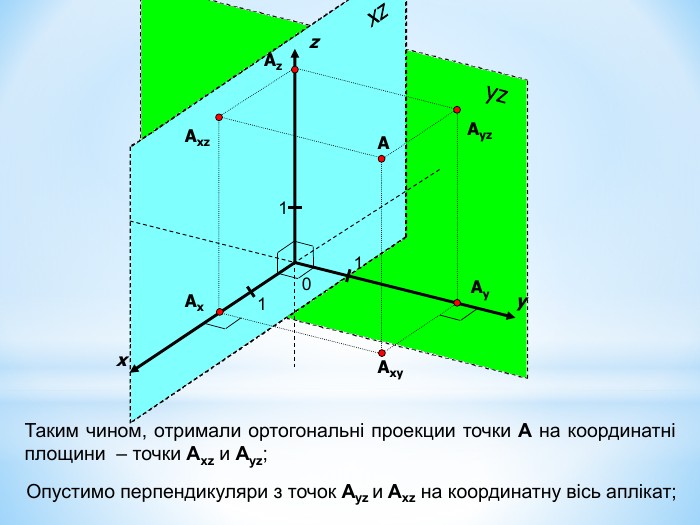
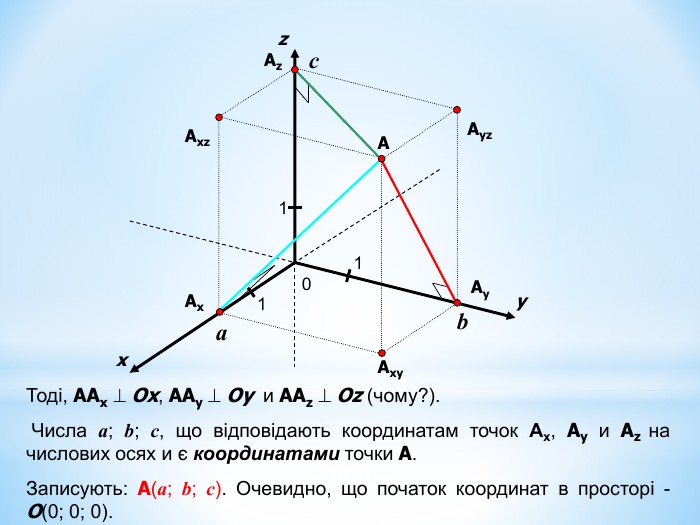
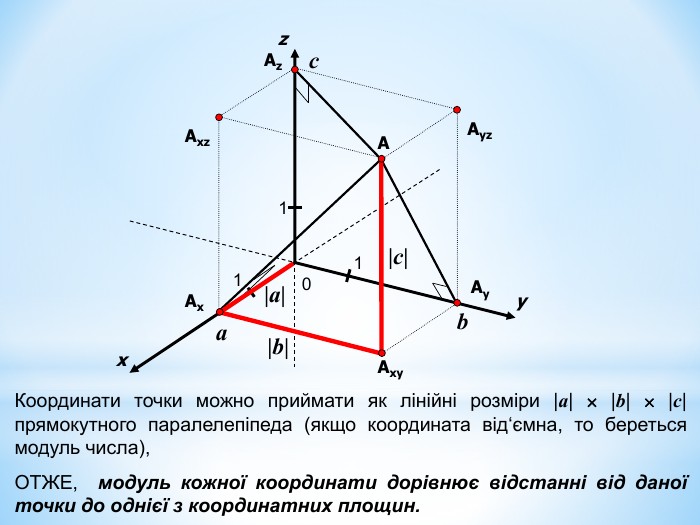
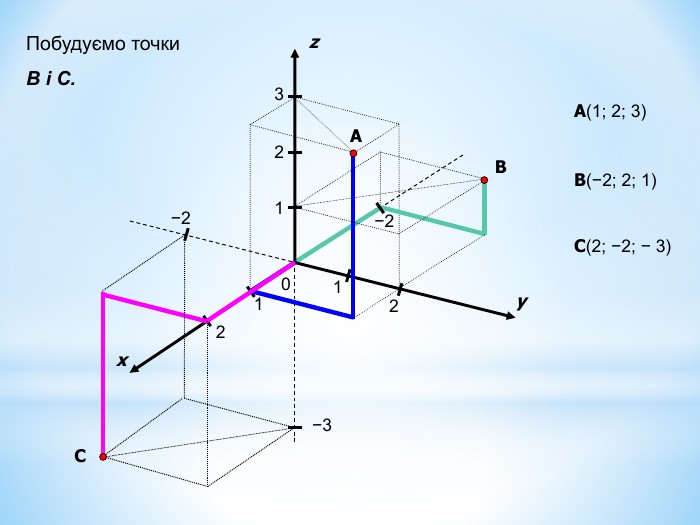
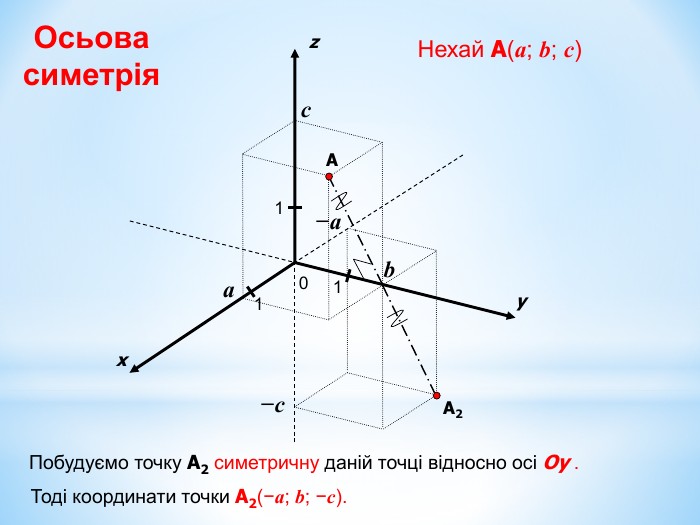
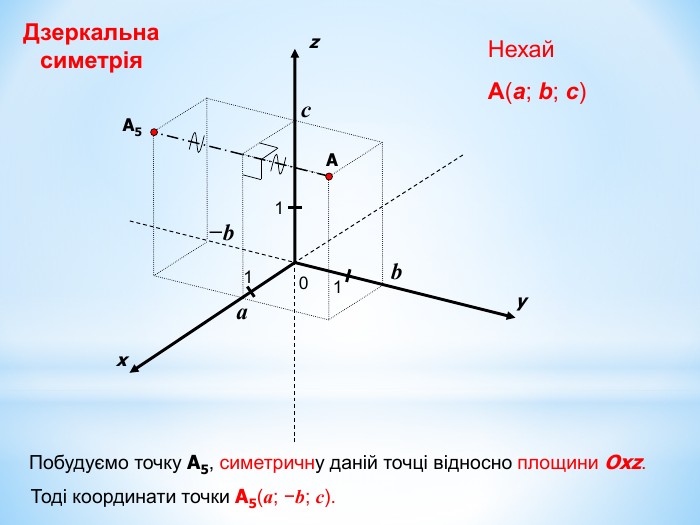
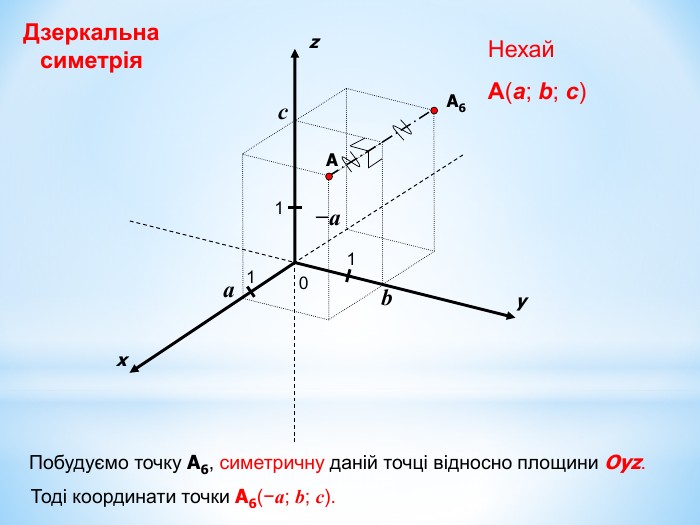
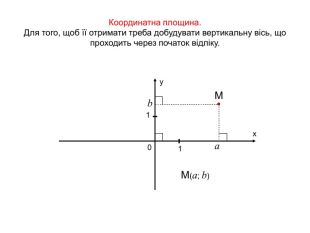
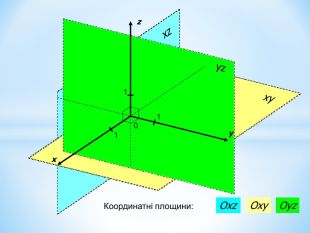
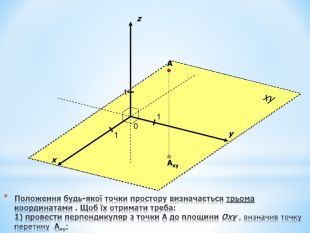
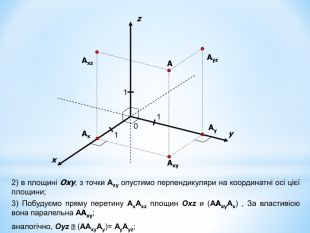
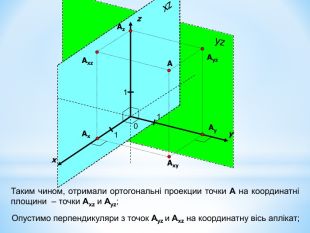
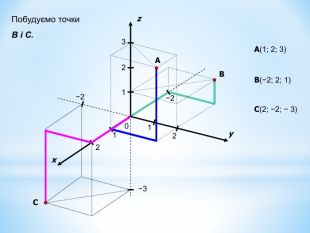
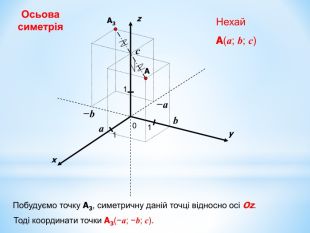
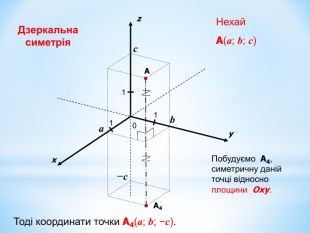
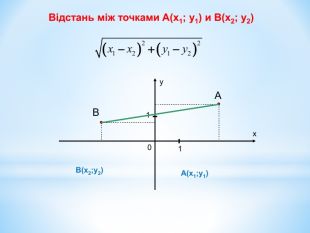
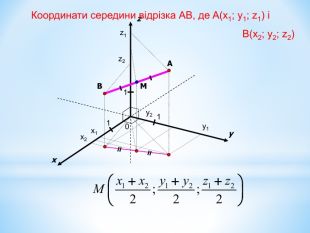
Анімована презентація для ознайомлення учнів з прямокутною системою координат в просторі, з поняттям симетрії в просторі; для навчання учнів умінню знаходити координати точок у просторі; будувати точки за їх координатами;знаходити відстань до осей ОХ,ОУ,OZ
координатних площин. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дякую! Прекрасна презентація.
-


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку