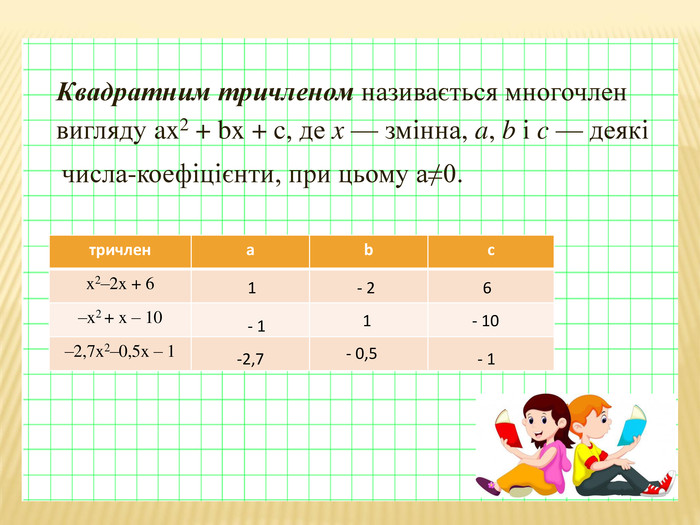
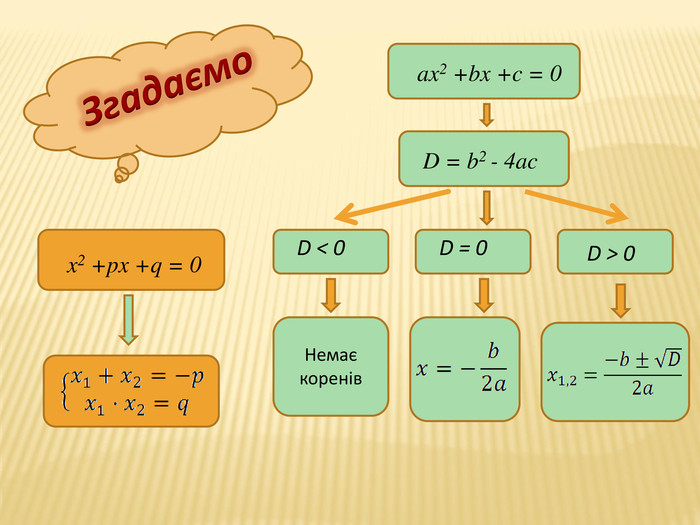
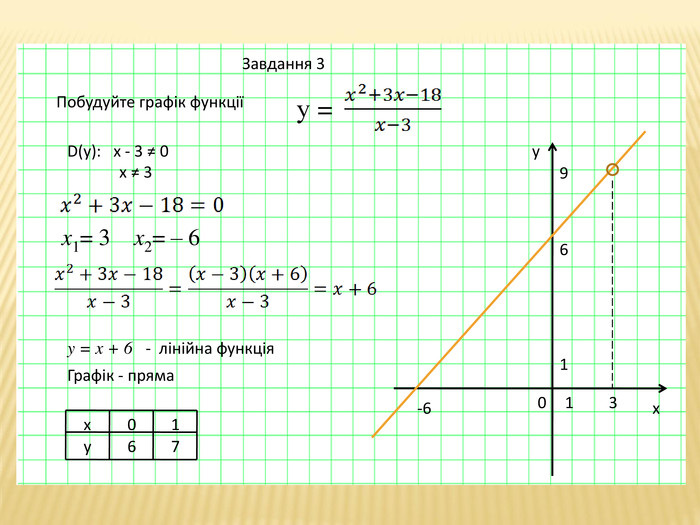
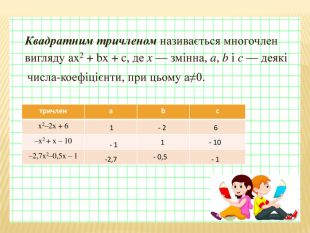
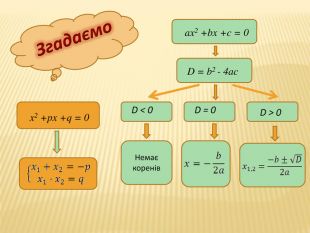
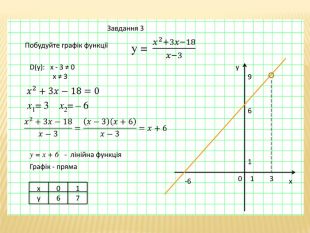
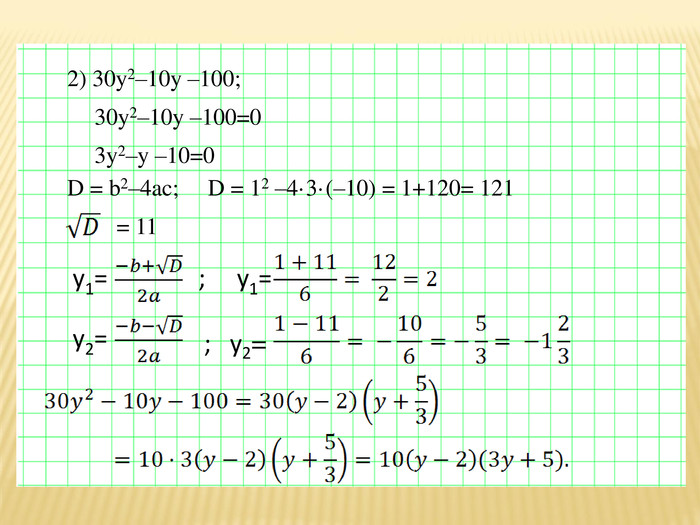Презентація для 8 класу "Квадратний тричлен"
Про матеріал
Даний урок можна використовувати для узагальнення темі "Квадратний тричлен" або при півторенні вивченного матеріалу. Подані розв'язування різноманітних завдань з цієї теми Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку