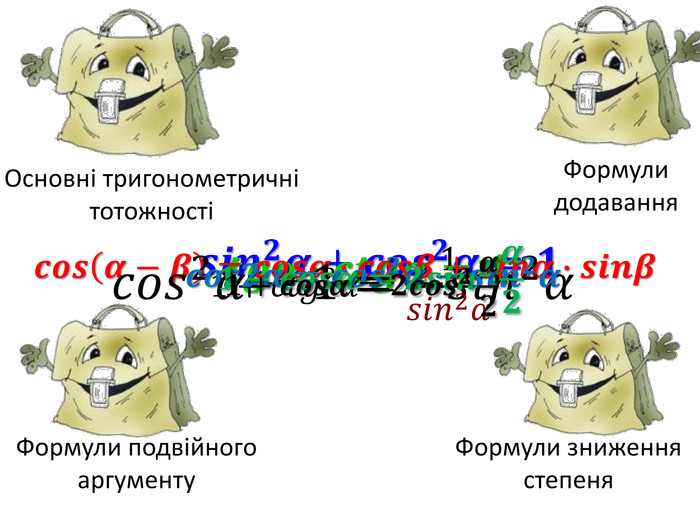
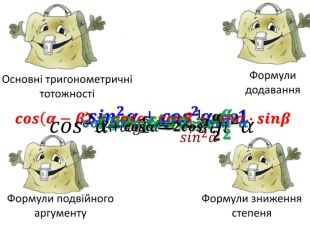
Презентація до теми "Формули подвійного аргументу. Формули зниження степеня"
На початку заняття доцільно повторити формули додавання, а потім переходити до вивчення наступних формул. Презентація містить багато практичних завдань, де з допомогою анімації легко пояснити їх розв'язання.






























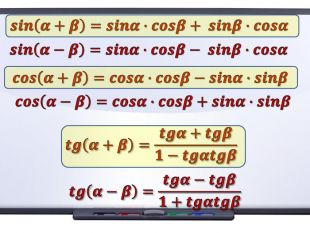
Cпростіть вираз:𝐬𝐢𝐧𝟕𝝅𝟐+𝜶−𝐜𝐨𝐬𝟓𝝅−𝜶+𝒕𝒈𝟔𝝅+𝜶−𝒄𝒕𝒈𝟗𝝅𝟐−𝜶= IV чв. – ІІ чв. – І чв. +І чв. +=−𝒄𝒐𝒔𝜶 +𝒄𝒐𝒔𝜶 +𝒕𝒈𝜶 −𝒕𝒈𝜶 = 0𝐬𝐢𝐧𝟑𝝅𝟐+𝜶∙𝐜𝐨𝐬𝝅−𝜶+𝐬𝐢𝐧𝟑𝝅−𝜶∙𝐜𝐨𝐬𝟏𝟏𝝅𝟐+𝜶= IV чв. – ІІ чв. – ІІ чв. + IV чв.+=−𝒄𝒐𝒔𝜶 𝒄𝒐𝒔𝟐𝜶+𝒔𝒊𝒏𝟐𝜶= 1 Формули зведення. Тригономет-ричне коло∙−𝒄𝒐𝒔𝜶 + 𝒔𝒊𝒏𝜶 ∙𝒔𝒊𝒏𝜶= Основні тригонометричні тотожностіstyle.colorfillcolorfill.typefill.on
𝒄𝒐𝒔𝝅𝟔−𝜶+𝒄𝒐𝒔𝝅𝟔+𝜶= Cпростіть вираз:𝒄𝒐𝒔𝝅𝟔𝒄𝒐𝒔𝜶+𝒔𝒊𝒏𝝅𝟔𝒔𝒊𝒏𝜶 + + 𝒄𝒐𝒔𝝅𝟔𝒄𝒐𝒔𝜶−𝒔𝒊𝒏𝝅𝟔𝒔𝒊𝒏𝜶 = 𝟐𝒄𝒐𝒔𝝅𝟔𝒄𝒐𝒔𝜶 =3 𝒄𝒐𝒔𝜶 𝐬𝐢𝐧𝛑𝟒−𝛂−𝐬𝐢𝐧𝛑𝟒+𝛂= 𝒔𝒊𝒏𝝅𝟒𝒄𝒐𝒔𝜶−𝒔𝒊𝒏𝜶𝒄𝒐𝒔𝝅𝟒 − −𝒔𝒊𝒏𝝅𝟒𝒄𝒐𝒔𝜶+𝒔𝒊𝒏𝜶𝒄𝒐𝒔𝝅𝟒 =𝒔𝒊𝒏𝝅𝟒𝒄𝒐𝒔𝜶−𝒔𝒊𝒏𝜶𝒄𝒐𝒔𝝅𝟒− −𝟐∙𝟐𝟐𝒔𝒊𝒏𝜶= =−𝟐𝒔𝒊𝒏𝜶 −𝒔𝒊𝒏𝝅𝟒𝒄𝒐𝒔𝜶−𝒔𝒊𝒏𝜶𝒄𝒐𝒔𝝅𝟒 Формули додавання. Значення тригонометричних функцій деяких кутів= 𝟐∙𝟑𝟐𝒄𝒐𝒔𝜶 =−𝟐𝒔𝒊𝒏𝜶𝒄𝒐𝒔𝝅𝟒=
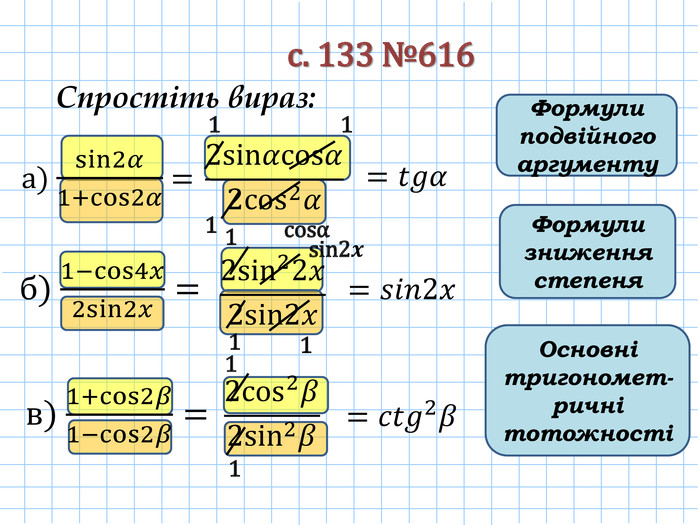
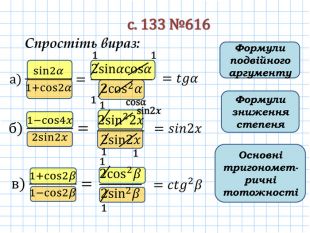
Застосовуючи формули подвійного аргументу, знайдіть значення виразу:а)sin𝛼=sin2⋅𝛼2= ……...….. 𝒔𝒊𝒏𝟐𝜶=𝟐𝒔𝒊𝒏𝜶𝒄𝒐𝒔𝜶 2𝑠𝑖𝑛𝛼2𝑐𝑜𝑠𝛼2; б)sin3𝛼=sin2⋅32𝛼= ……………….. 2𝑠𝑖𝑛32𝛼𝑐𝑜𝑠32𝛼; в)sin4𝛼=sin2⋅2𝛼= ………………… 2𝑠𝑖𝑛2𝛼𝑐𝑜𝑠2𝛼 =4sin𝛼cos𝛼cos2𝛼; г)cos3𝛼=cos2⋅32𝛼= ……………… =1−2sin232𝛼; cos232𝛼−sin232𝛼 =2cos232𝛼−1 = д)cos4𝛼= ………….. = ………… cos2⋅2𝛼 =1−2sin22𝛼. cos22𝛼−sin22𝛼 = =2cos22𝛼−1 Формули подвійного аргументу
Формули скороченого множення(a + b)2 = a2 + 2ab + b2 – квадрат суми;(a – b)2 = a2 – 2ab + b2 – квадрат різниці;a2 – b2 = (a + b)(a – b) – різниця квадратів;a3 + b3 = (a + b)(a2 – ab + b2) – сума кубів;a3 – b3 = (a – b)(a2 + ab + b2) – різниця кубів;(a + b)3 = a3 + 3a2b + 3ab2 + b3 – куб суми;(a – b)3 = a3 – 3a2b + 3ab2 – b3 – куб різниці.
Якщо гострий кут 𝜶 добудовується до горизонтального діаметра, то назва функції не змінюється. Якщо гострий кут 𝜶 добудовується до вертикального діаметра, то назва функції змінюється на кофункцію. У правій частині виразу ставиться знак, який має функція, що задана в умові. Правила зведення


про публікацію авторської розробки
Додати розробку






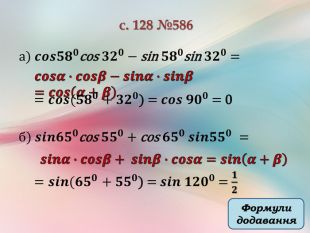























-

Гозян Тетяна
11.02.2024 в 13:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Забара Ольга
22.01.2024 в 22:18
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кухтін Юлія Олександрівна
11.01.2023 в 11:11
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Асєєва Ірина
28.03.2022 в 18:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Людмила Гелетей
24.02.2022 в 21:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Опята Людмила
26.10.2021 в 20:55
Дякую за презентацію. СУПЕР.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Бершеда Людмила Олександрівна
26.01.2021 в 23:38
Дякую за презентацію!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Роман Людмила
24.01.2021 в 20:45
Величезне спасибі !
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kozlovska Glalyna
19.01.2021 в 15:45
Дякую за презентацію!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Дмитренко Людмила Миколаївна
18.01.2021 в 21:12
Дякую автору за чудовий матеріал !
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ільченко Лариса
09.01.2021 в 22:32
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 8 відгуків