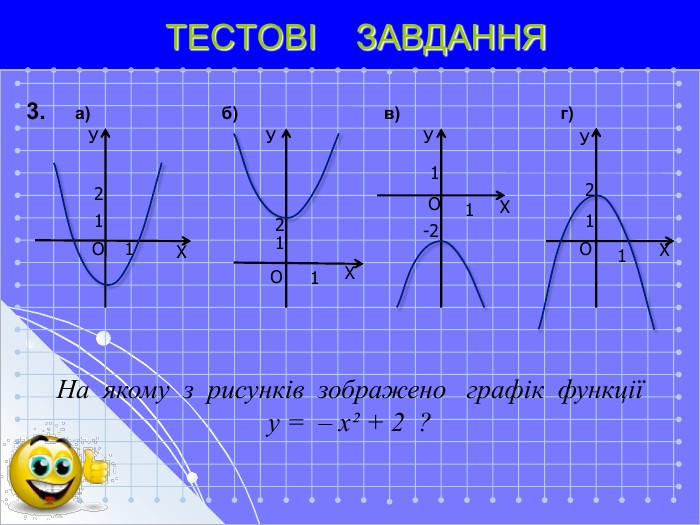
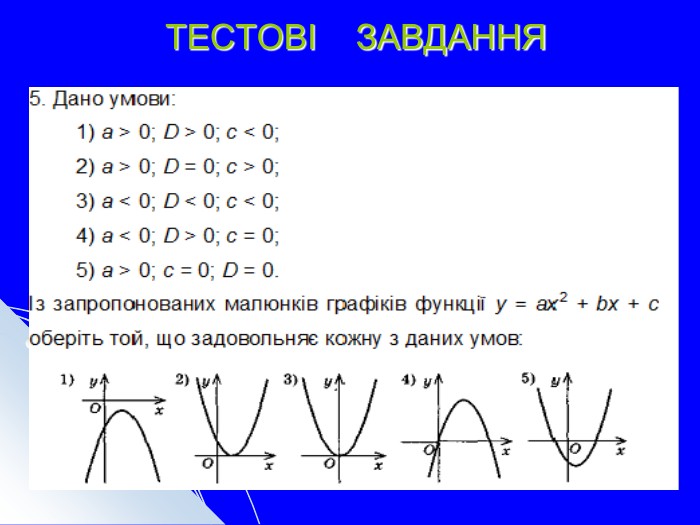
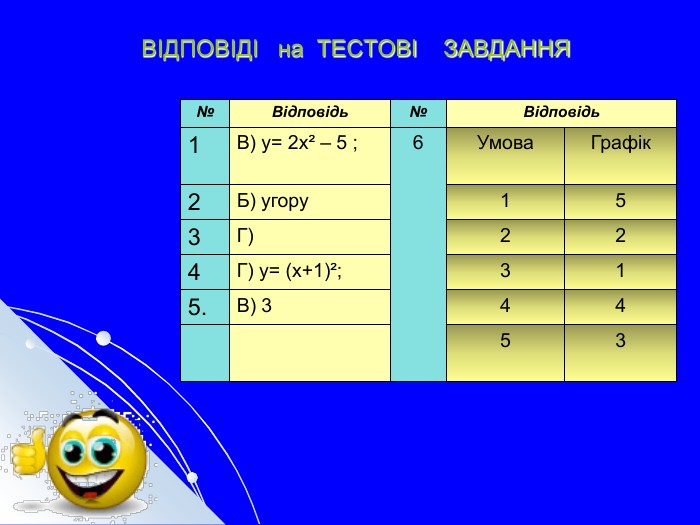
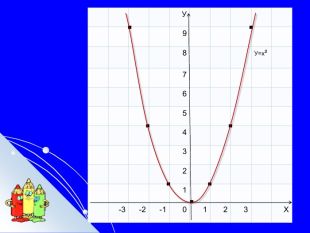
Презентація до теми "Квадратична функція"
Про матеріал
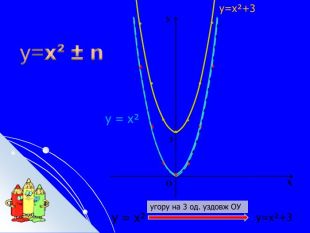
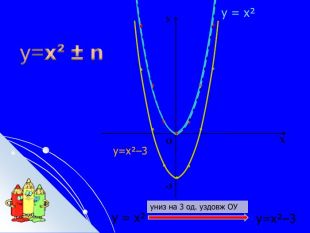
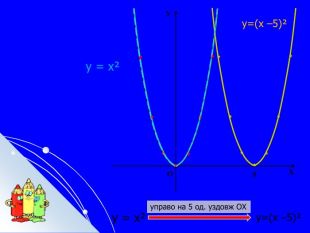
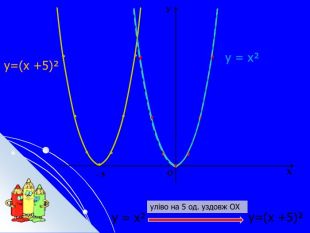
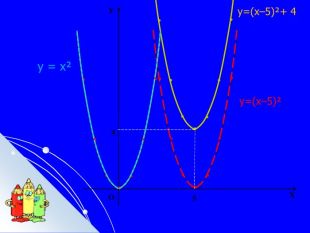
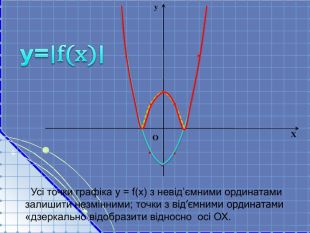
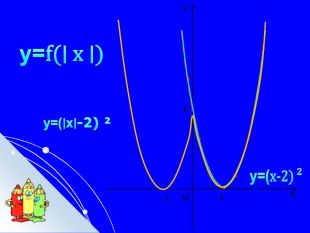
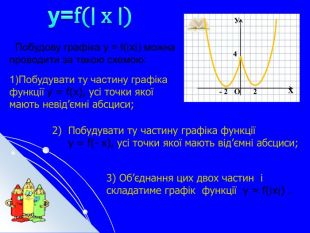
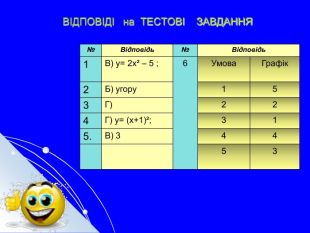
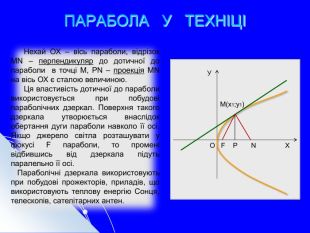
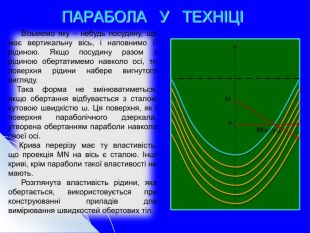
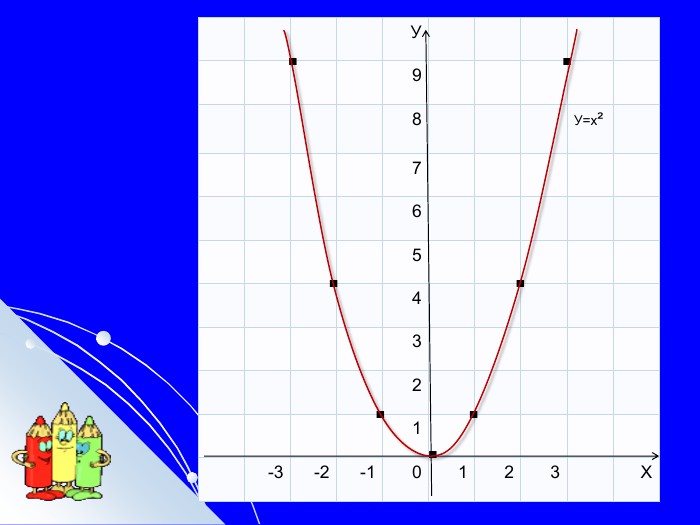
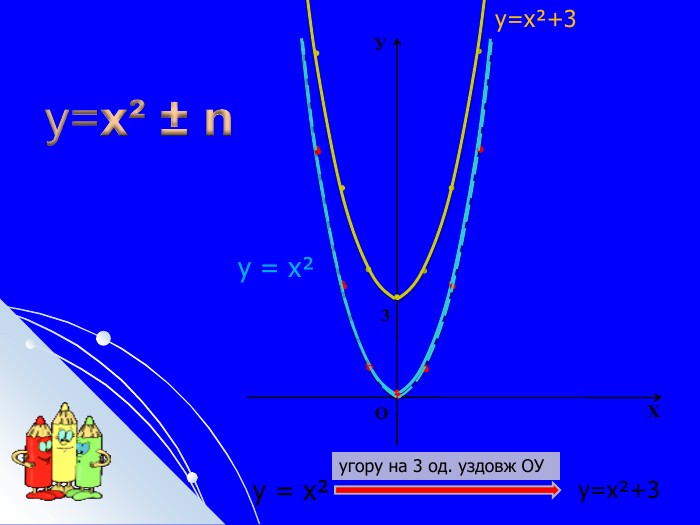
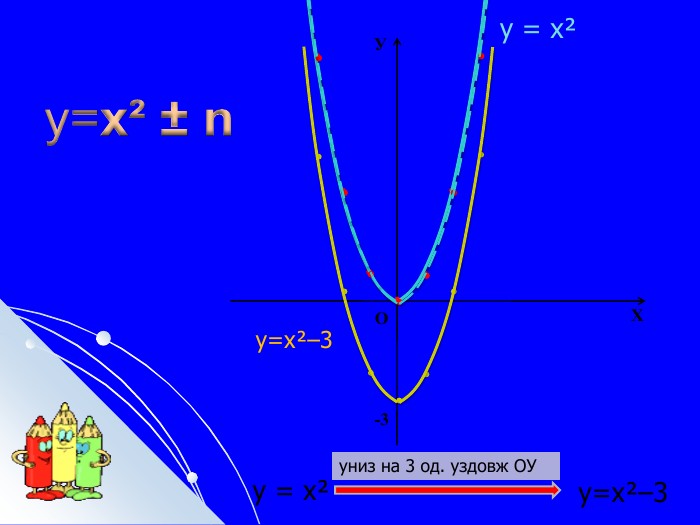
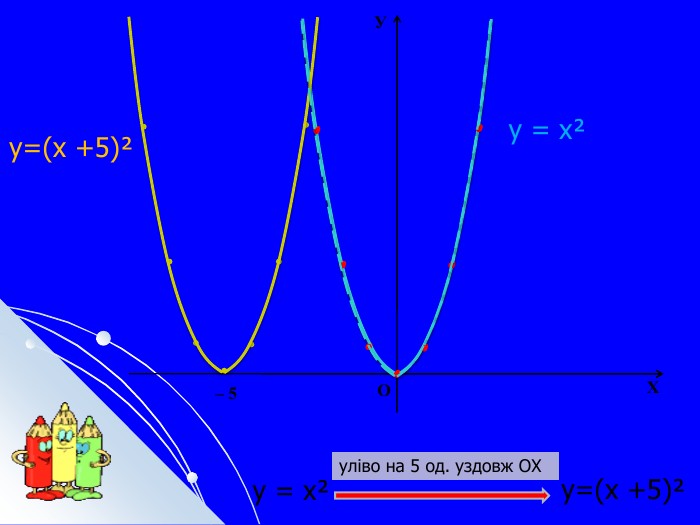
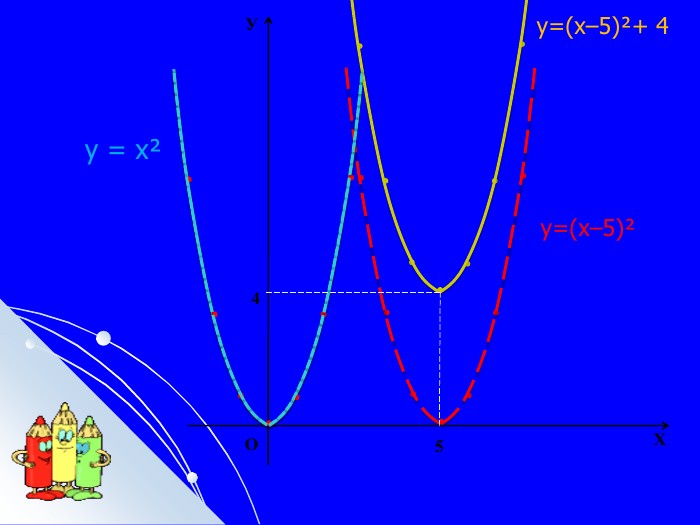
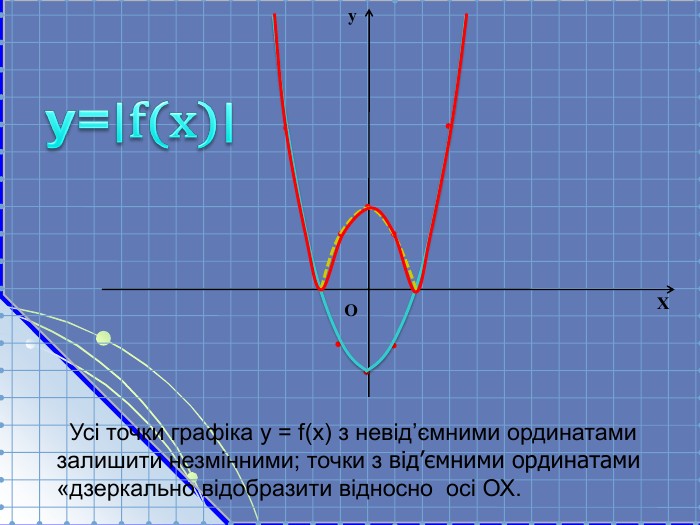
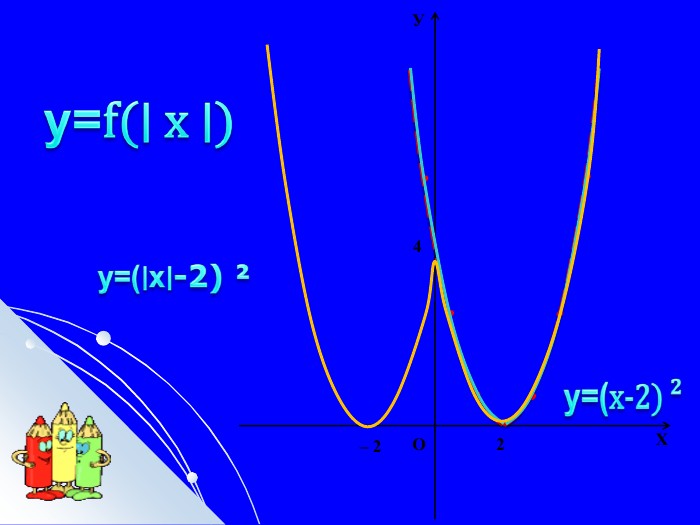
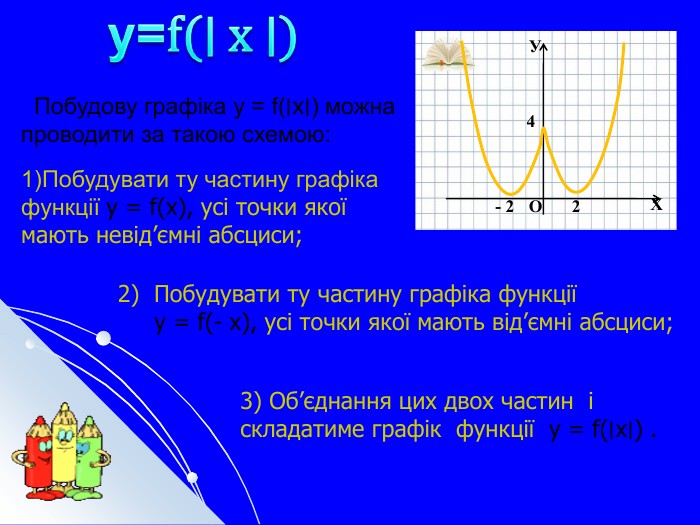
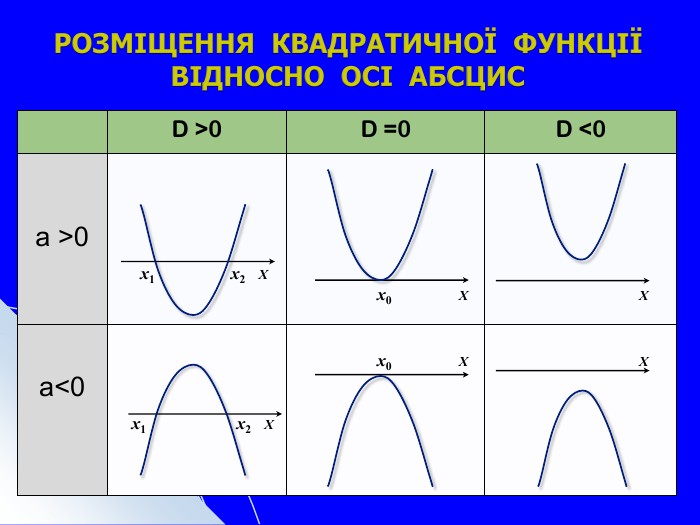
Складається із 35 слайдів з анімаціями. Слайди допоможуть учням скласти та записати алгоритм побудови графіка квадратичної функції та ілюструють застосування паралельного перенесення уздовж координатних осей для побудови графіка різних видів квадратичної функції, у т.ч. із зовнішнім і внутрішнім модулями. Також наведено приклади розв'язування завдань на знаходження нулів функції, проміжків зростання і спадання, знакосталості. Презентація містить відомості про застосування графіка квадратичної функції в архітектурі, інженерії. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
11. Квадратична функція, її графік і властивості Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку








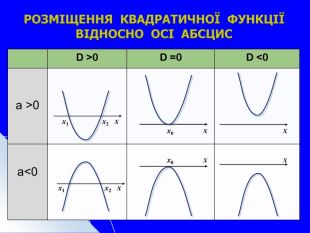
![а > 0 а < 0 1. D(y) = R 2. Е(у) = [у0; +∞) 1. D(y) = R 2. Е(у) = (-∞; y0] (х0 — абсциса вершини параболи, у0 — ордината вершини параболи) 3. а) Функція зростає, якщо х [х0; +∞) б) Функція спадає, якщо х (-∞; х0] 3. а) Функція зростає, якщо х (-∞; х0] б) Функція спадає, якщо х [х0; +∞) а > 0 а < 0 1. D(y) = R 2. Е(у) = [у0; +∞) 1. D(y) = R 2. Е(у) = (-∞; y0] (х0 — абсциса вершини параболи, у0 — ордината вершини параболи) 3. а) Функція зростає, якщо х [х0; +∞) б) Функція спадає, якщо х (-∞; х0] 3. а) Функція зростає, якщо х (-∞; х0] б) Функція спадає, якщо х [х0; +∞)](/uploads/files/206395/330481/371657_images/17.jpg)

![ПРИКЛАД 1 Розв’язання: а) оскільки а = –3 , гілки параболи напрямлені вниз, функція зростає, якщо х Є ( – ∞ ; 2] , функція спадає, якщо х Є [2; + ∞). б) оскільки а = –3 , гілки параболи напрямлені вниз, тому функція набуває найбільшого значення у вершині: у0= –3∙22+12∙2+1=13. Отже, найбільше значення функції у = 13. в) кількість нулів квадратичної функції залежить від знаку дискримінанту відповідного квадратного рівняння, у нашому випадку другий коефіцієнт парний, тому скористаємось формулою: Функція має два нулі. ПРИКЛАД 1 Розв’язання: а) оскільки а = –3 , гілки параболи напрямлені вниз, функція зростає, якщо х Є ( – ∞ ; 2] , функція спадає, якщо х Є [2; + ∞). б) оскільки а = –3 , гілки параболи напрямлені вниз, тому функція набуває найбільшого значення у вершині: у0= –3∙22+12∙2+1=13. Отже, найбільше значення функції у = 13. в) кількість нулів квадратичної функції залежить від знаку дискримінанту відповідного квадратного рівняння, у нашому випадку другий коефіцієнт парний, тому скористаємось формулою: Функція має два нулі.](/uploads/files/206395/330481/371657_images/19.jpg)