Презентація до теми "Многокутник"
Про матеріал
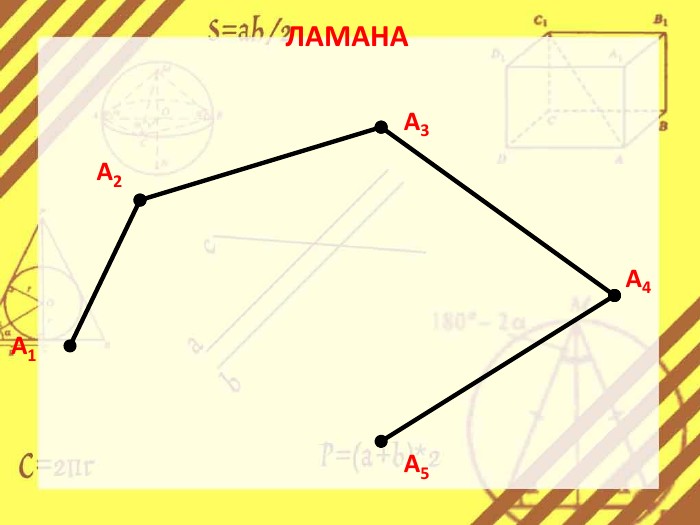
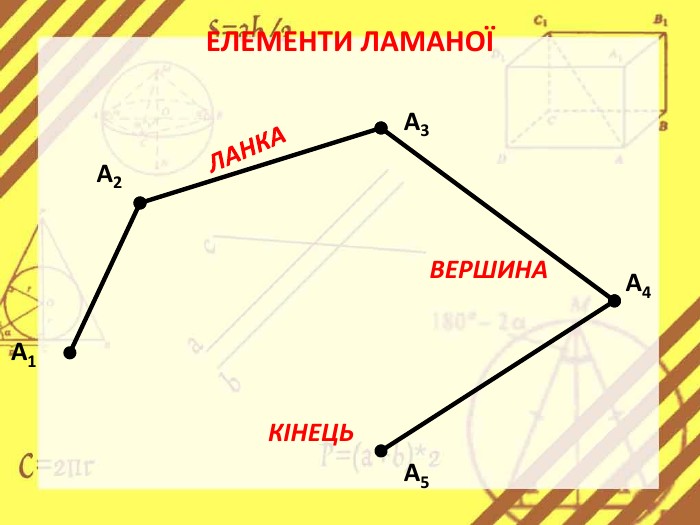
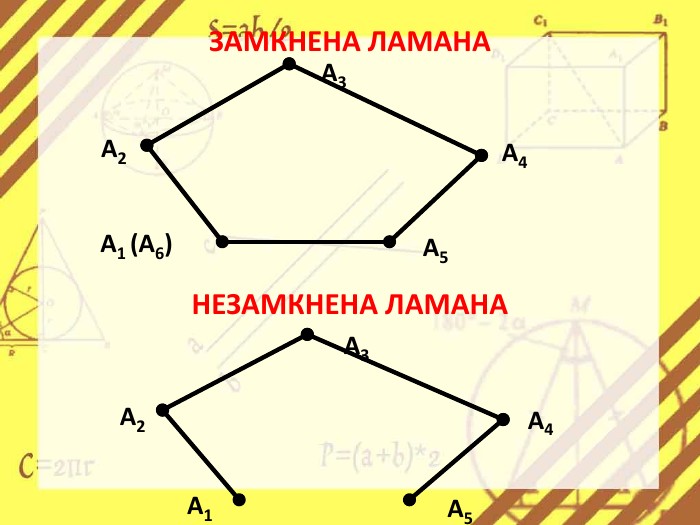
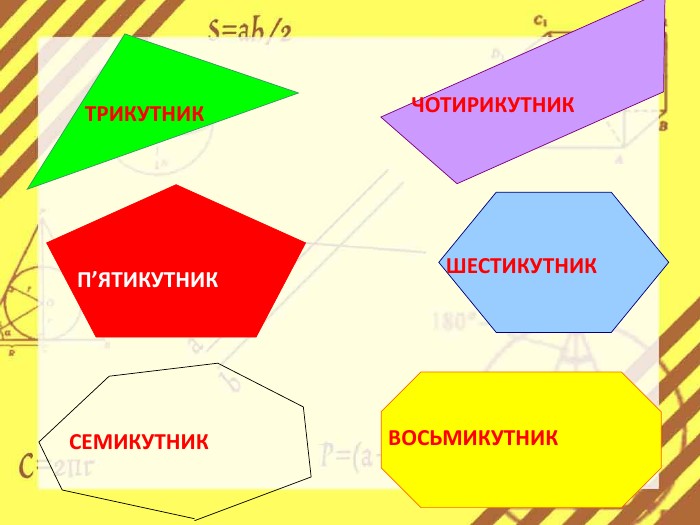
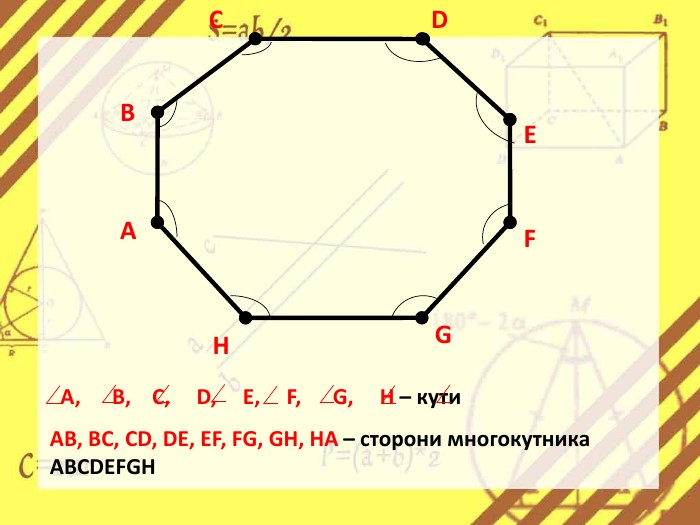
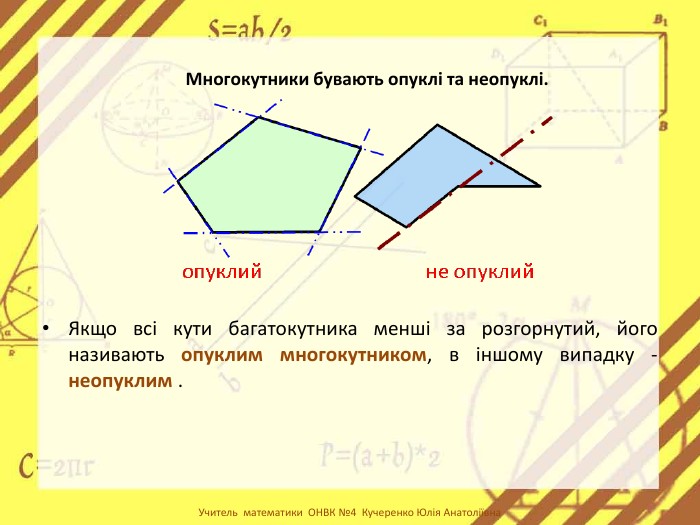
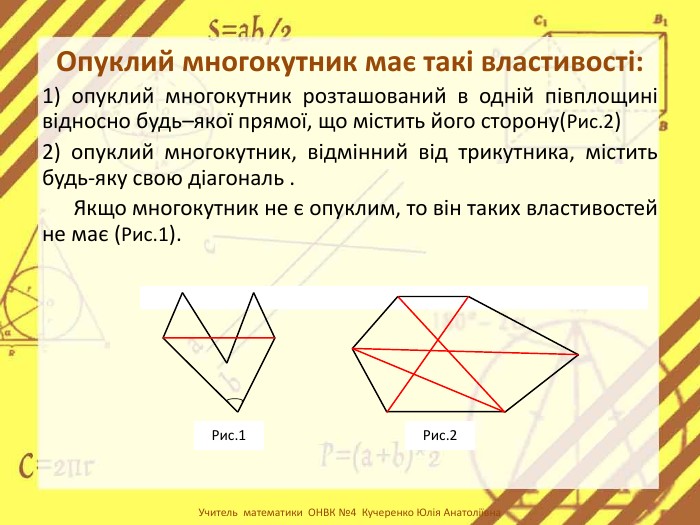
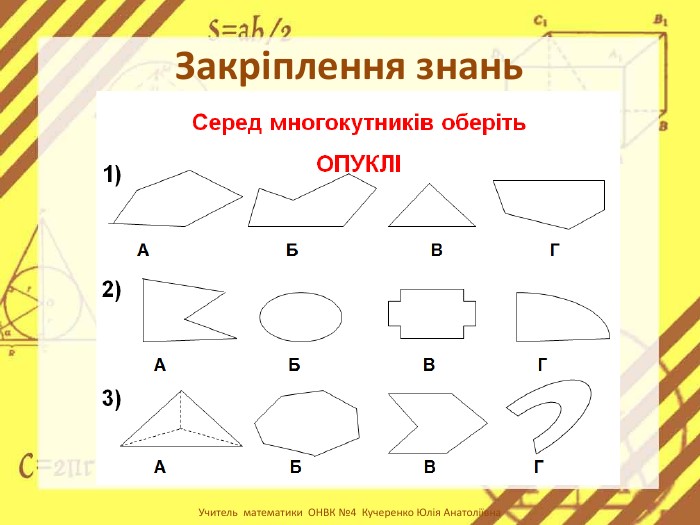
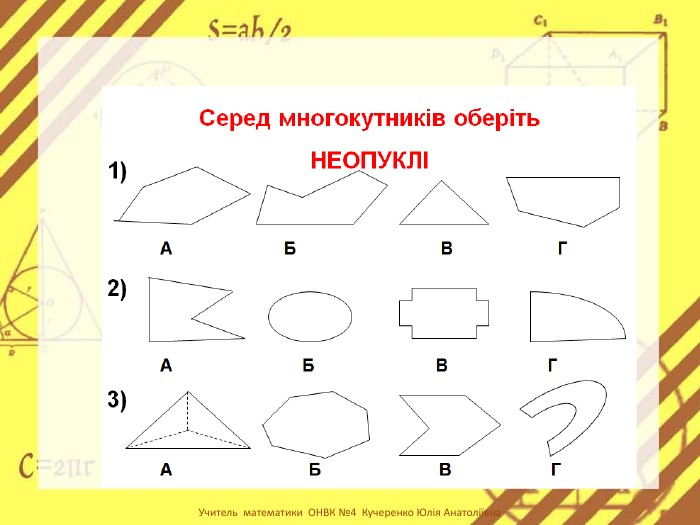
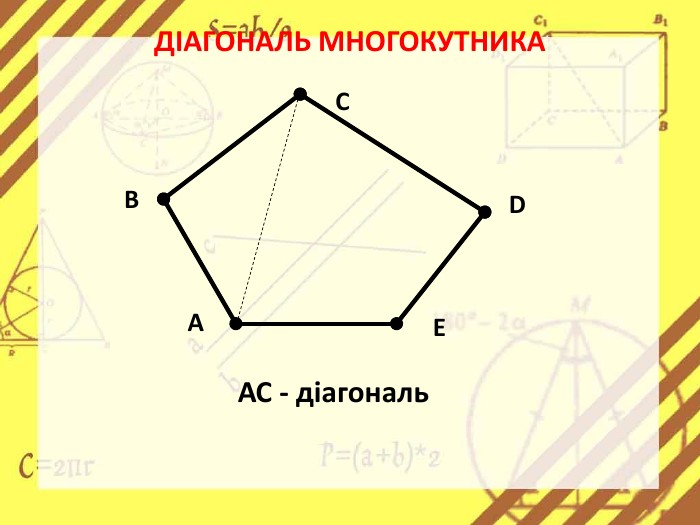
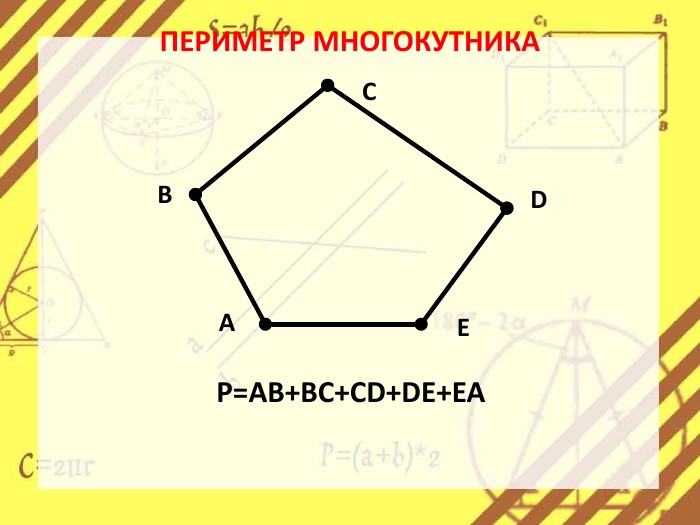
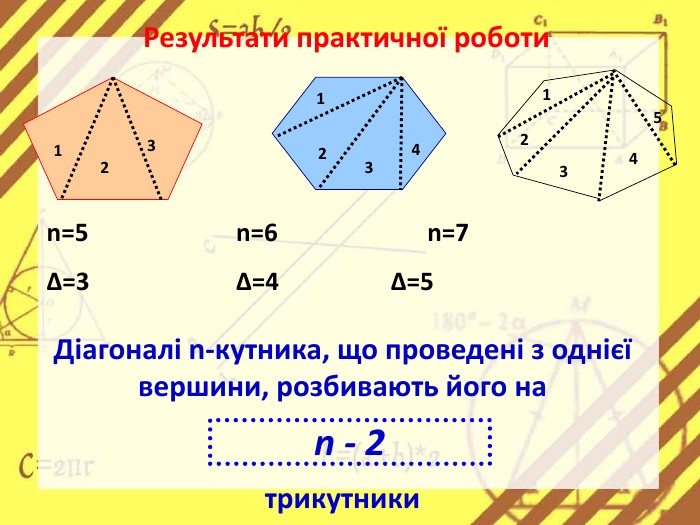
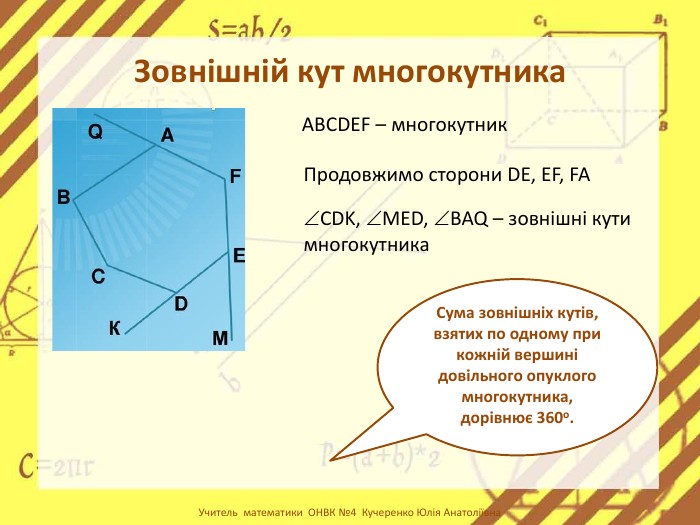
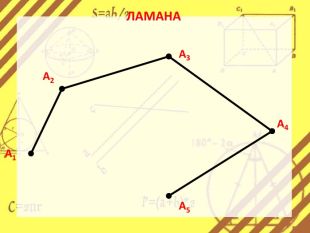
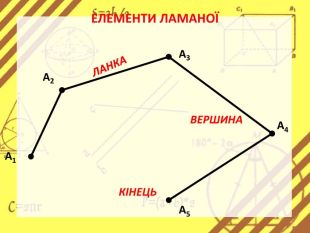
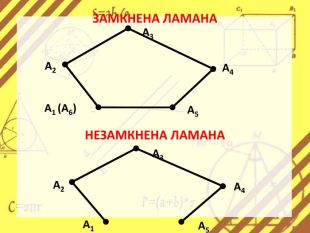
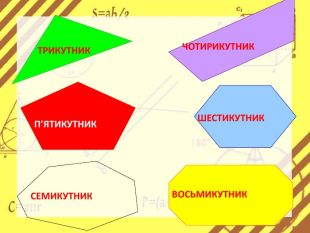
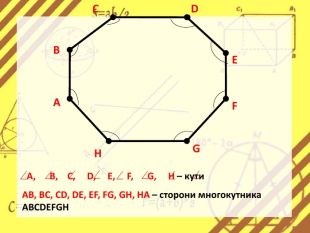
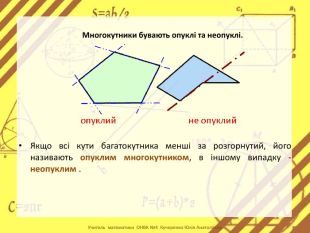
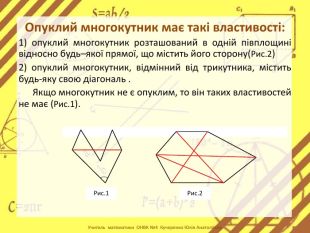
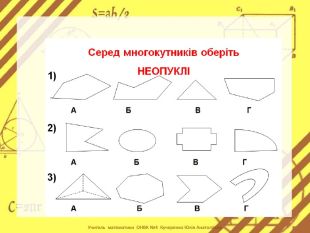
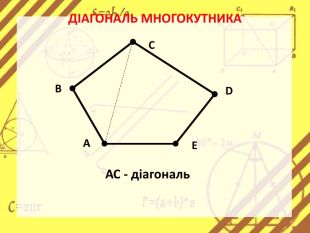
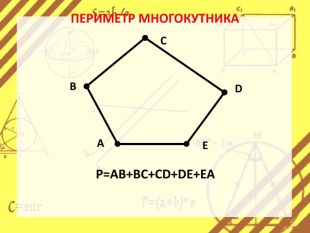
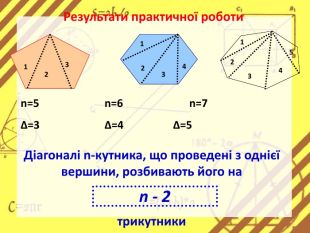
Презентація стане в нагоді вчителям при ознайомленні учнів з поняттям многокутника, видами многокутників (опуклим і неопуклим).Містить задачі на знаходження суми кутів многокутника, завдання на перевірку існування многокутника за відомою сумою кутів. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку