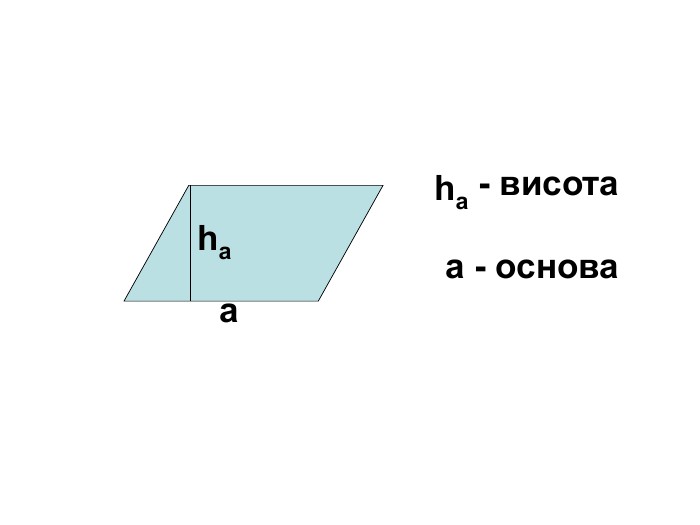
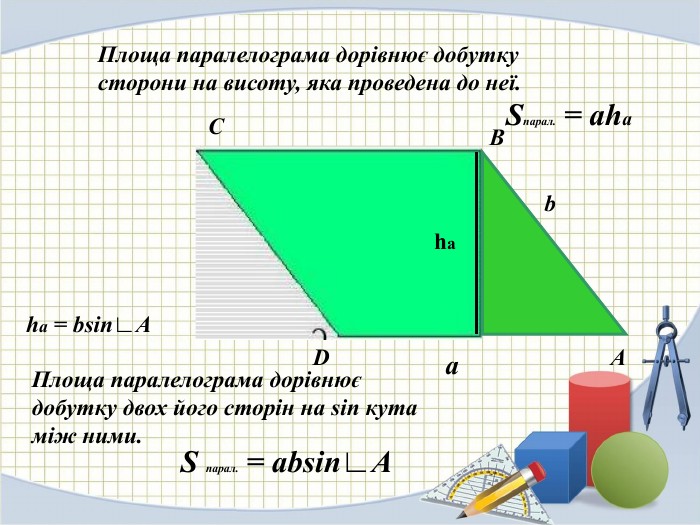
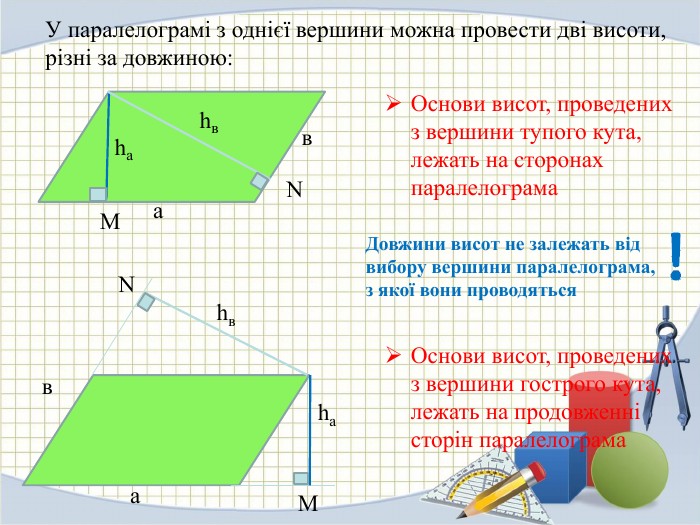
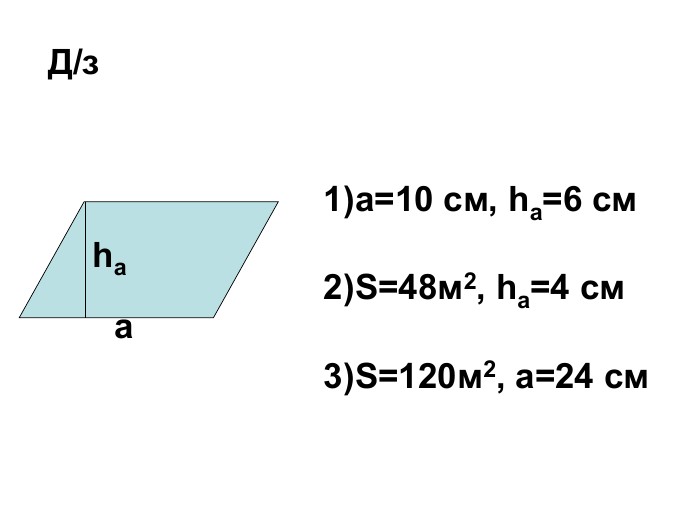
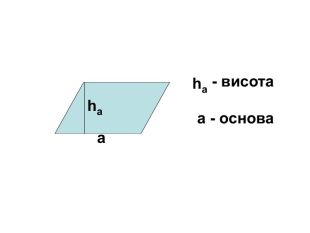
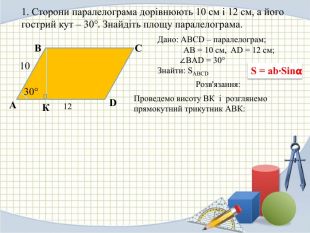
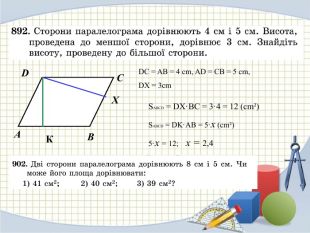
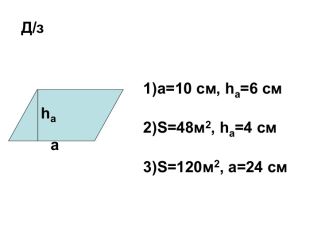
Презентація на тему "Площа паралелограма" 8 клас
Про матеріал
Презентація для ознайомлення учнів з формулами для знаходження площі паралелограма Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку