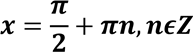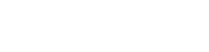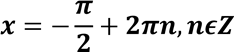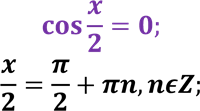Найпростіші тригонометричні рівняння

Презентація створена учителем математики

Матвійчук Тетяною Володимирівною

Означення:

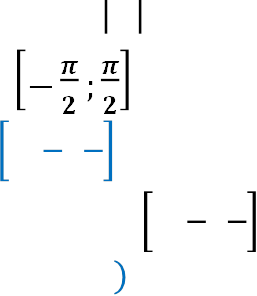Арксинусом числа  𝒃, де   𝒃 ≤ 𝟏 , називають таке число 𝜶 з проміжку ,  синус  якого дорівнює 𝒃.

𝝅 𝝅

                   𝒂𝒓𝒄𝒔𝒊𝒏 𝒃 = 𝜶, 𝜶 ∈    −    ;  , 𝐬𝐢𝐧 𝜶 = 𝒃, 𝒃 ≤ 𝟏.

𝟐 𝟐

                                                                                                                          𝟏 𝝅 𝝅                       𝝅 𝝅         𝝅 𝟏

                  Приклад: 𝒂𝒓𝒄𝒔𝒊𝒏  =    ,     ∈    −    ;  , 𝐬𝐢𝐧  =  .

                                                                                                                 𝟐          𝟔𝟔                    𝟐 𝟐                                                         𝟔            𝟐

                                                                                                     𝒂𝒓𝒄𝒔𝒊𝒏 −𝒃 = − 𝒂𝒓𝒄𝒔𝒊𝒏𝒃,

Приклад:  .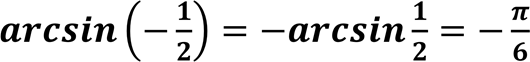

Означення:

Арккосинусом числа 𝒃, де  𝒃 ≤ 𝟏, називають таке число  𝜶 з проміжку 𝟎; 𝝅 , косинус якого дорівнює 𝒃.

                                    𝒂𝒓𝒄𝒄𝒐𝒔 𝒃 = 𝜶, 𝜶𝝐𝟎; 𝝅 , 𝐜𝐨𝐬 𝜶 = 𝒃,    𝒃 ≤ 𝟏.

Приклад:  .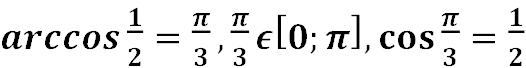

𝒂𝒓𝒄𝒄𝒐𝒔 −𝒃 = 𝝅 − 𝒂𝒓𝒄𝒄𝒐𝒔𝒃,

                                                                                                                          𝟏                                  𝟏                                              𝝅                                 𝟐

                                                              𝒂𝒓𝒄𝒄𝒐𝒔   −   = 𝝅 − 𝒂𝒓𝒄𝒄𝒐𝒔  = 𝝅 −  =  𝝅.

                                                                                                                          𝟐                                  𝟐                                              𝟑                                  𝟑

                                   Але: 𝒂𝒓𝒄𝒄𝒐𝒔 −𝟏    = 𝝅, 𝝅𝝐𝟎; 𝝅, 𝐜𝐨𝐬 𝝅 = −𝟏.

Означення:

Арктангенсом числа  𝒃, називають таке число 𝜶 з проміжку 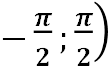,  тангенс  якого дорівнює 𝒃.

Приклад: .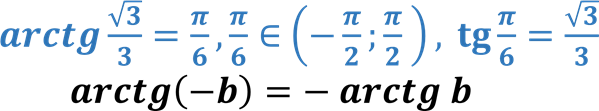

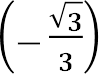                                                                                                                                                                                                                               𝟑 𝝅

                            Приклад: 𝒂𝒓𝒄𝒕𝒈                = −𝒂𝒓𝒄𝒕𝒈 = −  .

                                                                                                                                                                                                                            𝟑   𝟔

Означення:

Арккотангенсом числа  𝒃, називають таке число 𝜶 з проміжку 𝟎; 𝝅,  котангенс  якого дорівнює 𝒃. 𝒂𝒓𝒄𝒄𝒕𝒈 𝒃 = 𝜶, 𝐜𝐭𝐠𝜶 = 𝒃, 𝜶 ∈ 𝟎; 𝝅

Приклад:  .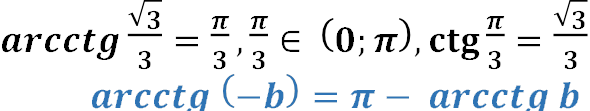

Приклад:

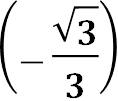                                                                                                                                                                                                              𝟑                                                                             𝝅  𝟐𝝅

                             𝒂𝒓𝒄𝒄𝒕𝒈                  = 𝝅 − 𝒂𝒓𝒄𝒄𝒕𝒈    = 𝝅 −  =  .

                                                                                                                                                                                                          𝟑                                                                            𝟑       𝟑

Обчислити усно:

𝟏) 𝒂𝒓𝒄𝒔𝒊𝒏𝟎;

𝟑

𝟐) 𝒂𝒓𝒄𝒄𝒐𝒔;

𝟐

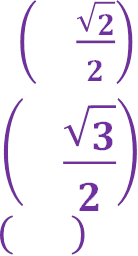                             𝟑) 𝒂𝒓𝒄𝒔𝒊𝒏 −         ;

                        𝟒) 𝒂𝒓𝒄𝒄𝒐𝒔 −          ;

5) 𝒂𝒓𝒄𝒔𝒊𝒏 −𝟏 ;

𝟏 𝟐

𝟔) 𝒂𝒓𝒄𝒄𝒐𝒔;

𝐜𝐨𝐬 𝒙 = 𝒃, 𝒃 ≤ 𝟏 → 𝒙 = ±𝒂𝒓𝒄𝒄𝒐𝒔𝒃 + 𝟐𝝅𝒏, 𝒏𝝐𝒁.

Приклад:

;                         

;

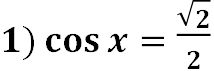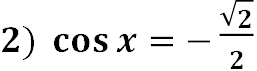
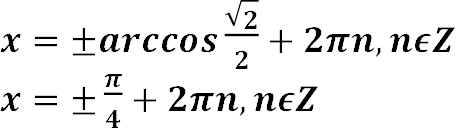𝐬𝐢𝐧 𝒙 = 𝒃, 𝒃 ≤ 𝟏 → 𝒙 = −𝟏^𝒌𝒂𝒓𝒄𝒔𝒊𝒏𝒃 + 𝝅𝒌, 𝒌𝝐𝒁;

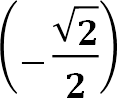                                          𝟑) 𝒔𝒊𝒏 𝒙 = −     ^𝟐 ; 𝒙 = −𝟏^𝒌𝒂𝒓𝒄𝒔𝒊𝒏                  + 𝝅𝒌, 𝒌𝝐𝒁;

𝟐

𝒙 = −−𝟏 ^𝒌𝝅 + 𝝅𝒌, 𝒌𝝐𝒁; 𝒙 = −𝟏^{𝒌+𝟏𝝅} + 𝝅𝒌, 𝒌𝝐𝒁.

𝟒𝟒

𝐭𝐠 𝒙 = 𝒃 → 𝒙 = 𝒂𝒓𝒄𝒕𝒈𝒃 + 𝝅𝒏, 𝒏𝝐𝒁, ∀𝒃 ∈ 𝑹.

Приклад: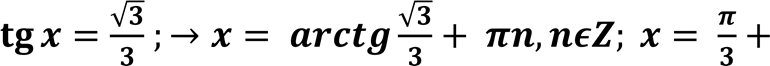

𝝅𝒏, 𝒏𝝐𝒁;

𝐜𝐭𝐠 𝒙 = 𝒃 → 𝒙 = 𝒂𝒓𝒄𝒄𝒕𝒈𝒃 + 𝝅𝒏, 𝒏𝝐𝒁, ∀𝒃 ∈ 𝑹. Приклад: 𝒄𝒕𝒈𝒙 = −  𝟑;

.

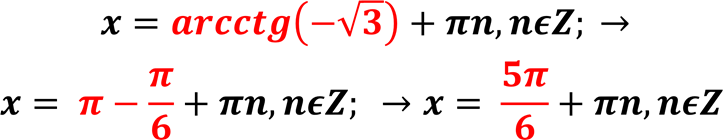Особливі випадки розв’язання тригонометричних рівнянь.

1.Опрацюйте   § 16 ст. 145 – 153, зверніть увагу на розв'язання Задач 1 – 5 .

2.Перегляньте презентацію та  відео за покликанням у Google classroom.

3. Виконайте самостійно: №16.4, №16.10, №16.16.

ДЯКУЮ ЗА УВАГУ!  БАЖАЮ УСПІХІВ!