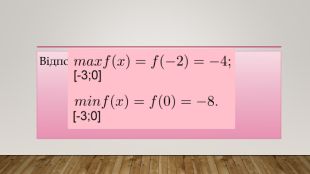Презентація до уроку алгебри 11 класу «Найбільше і найменше значення функції на відрізку"
Про матеріал
Презентація до уроку алгебри 11 класу «Найбільше і найменше значення функції на відрізку. Прикладні задачі на знаходження найбільшого і найменшого значень.»
Приклади задач з теми по підготовці до ЗНО Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


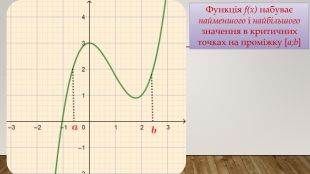
![Функція f(x) набуває найменшого і найбільшого значення в критичних точках на проміжку [a;b] Функція f(x) набуває найменшого і найбільшого значення в критичних точках на проміжку [a;b]](/uploads/files/489395/382081/436247_images/2.jpg)
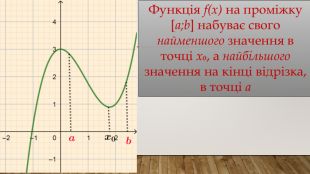
![Функція f(x) на проміжку [a;b] набуває свого найменшого значення в точці х₀, а найбільшого значення на кінці відрізка, в точці а Функція f(x) на проміжку [a;b] набуває свого найменшого значення в точці х₀, а найбільшого значення на кінці відрізка, в точці а](/uploads/files/489395/382081/436247_images/3.jpg)
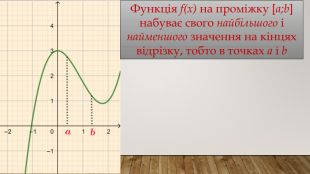
![Функція f(x) на проміжку [a;b] набуває свого найбільшого і найменшого значення на кінцях відрізку, тобто в точках a і b Функція f(x) на проміжку [a;b] набуває свого найбільшого і найменшого значення на кінцях відрізку, тобто в точках a і b](/uploads/files/489395/382081/436247_images/4.jpg)
![Алгоритм знаходження найбільшого і найменшого значення функції на відрізку 1) Знайти критичні точки функції f, які належать відрізку [a;b];2) Обчислити значення функції в знайдених критичних точках і на кінцях розглядуваного відрізка;3) З усіх знайдених значень обрати найбільше і найменше. Алгоритм знаходження найбільшого і найменшого значення функції на відрізку 1) Знайти критичні точки функції f, які належать відрізку [a;b];2) Обчислити значення функції в знайдених критичних точках і на кінцях розглядуваного відрізка;3) З усіх знайдених значень обрати найбільше і найменше.](/uploads/files/489395/382081/436247_images/5.jpg)
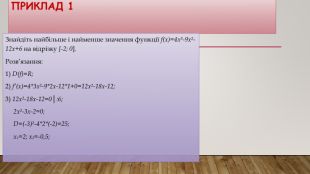
![Приклад 1 Знайдіть найбільше і найменше значення функції f(x)=4x³-9x²-12x+6 на відрізку [-2; 0]. Розв’язання:1) D(f)=R;2) f’(x)=4*3x²-9*2x-12*1+0=12x²-18x-12;3) 12x²-18x-12=0│:6; 2x²-3x-2=0; D=(-3)²-4*2*(-2)=25; x₁=2; x₂=-0,5; Приклад 1 Знайдіть найбільше і найменше значення функції f(x)=4x³-9x²-12x+6 на відрізку [-2; 0]. Розв’язання:1) D(f)=R;2) f’(x)=4*3x²-9*2x-12*1+0=12x²-18x-12;3) 12x²-18x-12=0│:6; 2x²-3x-2=0; D=(-3)²-4*2*(-2)=25; x₁=2; x₂=-0,5;](/uploads/files/489395/382081/436247_images/6.jpg)
![Отже, функція f має дві критичні точки, а проміжку [-2; 0] належіть одна: х= - 0,5. Маємо: Отже, Отже, функція f має дві критичні точки, а проміжку [-2; 0] належіть одна: х= - 0,5. Маємо: Отже,](/uploads/files/489395/382081/436247_images/7.jpg)
![Приклад 2 Знайдіть найбільше і найменше значення функції на проміжку [-3; 0]. Розв’язання:1)D(f)=R\{1};2)3)=0;ОДЗ: х≠1 Приклад 2 Знайдіть найбільше і найменше значення функції на проміжку [-3; 0]. Розв’язання:1)D(f)=R\{1};2)3)=0;ОДЗ: х≠1](/uploads/files/489395/382081/436247_images/8.jpg)
![х₁= - 2; х₂ = 4.4) Отже, функція f(x) має дві критичні точки, а проміжку [-3; 0] належіть одна x= -2. Маємо: х₁= - 2; х₂ = 4.4) Отже, функція f(x) має дві критичні точки, а проміжку [-3; 0] належіть одна x= -2. Маємо:](/uploads/files/489395/382081/436247_images/9.jpg)
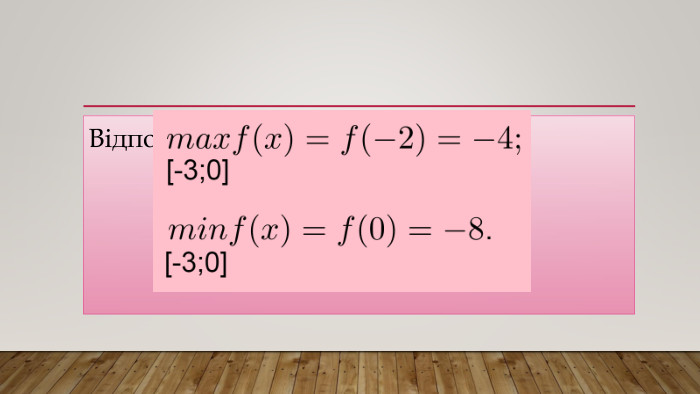




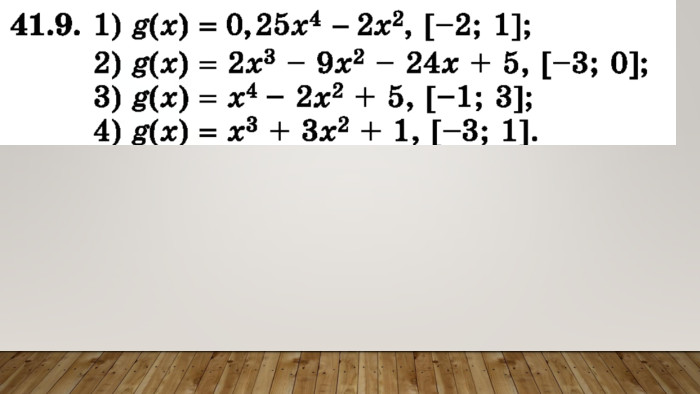


![Домашнє завдання. Знайдіть найбільше і найменше значення функції на вказаному відрізку:f(x)=3x²-x³, [-1;3];f(x)=x⁴-2x²+5, [0;2];f(x)=2x³+9x²-60x-7; [-1;3]. Домашнє завдання. Знайдіть найбільше і найменше значення функції на вказаному відрізку:f(x)=3x²-x³, [-1;3];f(x)=x⁴-2x²+5, [0;2];f(x)=2x³+9x²-60x-7; [-1;3].](/uploads/files/489395/382081/436247_images/18.jpg)