Урок "Показникова функція, її графік і властивості" для 11 класу

Конспект уроку №1

Тема: «Показникова функція, її графік і властивості»  Мета :

-                      навчальна: ввести поняття про показникову функцію, пояснити властивості та навчити будувати графік показникової функції, формувати вміння та навички застосовувати отримані знання для розв’язування задач прикладного характеру;

-                      розвивальна: розвивати логічне мислення, пізнавальну активність; 

-                      виховна: виховувати графічну культуру, увагу, культуру математичної мови.

Тип уроку: вивчення нового матеріалу.

Обладнання: Таблиця «Показникова функція».

 

Хід уроку І. Організаційний момент.

ІІ. Перевірка домашнього завдання.

ІІІ. Актуалізація опорних знань.

Вчитель шляхом фронтального опитування пригадує з учнями основні поняття. З функціональною лінією ви знайомитеся не вперше, тож дайте визначення поняттям: 

1)  Функція. 

2)  Область визначення функції. 

3)  Область значення функції. 

4)  Парність, непарність функції. 

5)  Проміжки монотонності функції. 

6)  Проміжки знакосталості функції. 

7)  Нулі функції. 

8)  Екстремуми функції.

ІV. Вивчення нового матеріалу

Означення показникової ф-ції:

Функція виду у=𝒂^𝒙, де а˃0, а≠1 називається показниковою (з основною а).

Усно.

➢Чи є дані функції показниковими? Якщо ні, то чому? (відповіді учнів)

1)   у=х² – ні

2)   у=3^х – так

3)   ^х – так

4)   у=1^х  - ні

5)   ^х – так

6)   у=(2,5)^х – так

7)   у=(-15)^х – ні

 

➢ Наведіть приклади показникових ф-цій.

Почнемо вивчення показникових ф-цій з ф-ції у=3^х.

 

Складемо таблицю:

Х	-2	-1	0	1	2
Y	1/9	1/3	1	3	9

 

           

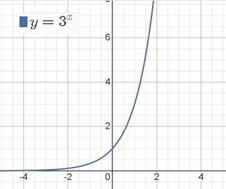Властивості:

1.                D(y)=R

2.                Е(y)= R+

3.                y = 3^х   áна R

4.                (0;1) – точка перетину з 0Y

 

•      Назвіть найбільше значення ф-ції (немає)

•      Назвіть найменше значення ф-ції. (немає)

5. max і min функція не має.

 

Усно. Порівняйте: 1) 3⁴ < 3⁸

2)   3√2 < 3√7

3)   3-1/2 ˃ 3-2

4)   30,5 < 32/3

5)   3ⁿ ˃ 3⁰

6)   3⁰ ˃ 3^-2

7)   3^α ˃ 3^β порівняти α і β  α ˃ β

 

Дивлячись на малюнок 87 стор. 191 (підручник) скажіть, що спільного і чим відрізняються функції та їх графіки. Побудуйте графік ф-ції y = ⁽¹)^х  

3

Складемо таблицю

Х	-2	-1	0	1	2
Y	9	3	1	1/3	1/9

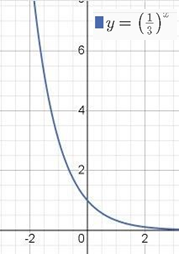                                                                   Властивості:

1.    D(y)=R

2.    E(y)= R+

3.    y = (¹)^х  â   на R

3

4.    (0;1) – точка перетину з OY

 

 

•      Назвіть найбільше значення ф-ції (немає)

•      Назвіть найменше значення ф-ції. (немає)

5. max і min функція не має.

 

Усно. Порівняйте:

1)   (1/3)⁵ ˃ (1/3)⁷

2)   0,2³ < 0,2^-4

3)   (1/3)² ˃ (1/3)⁴

4)   0,4^-3 ˃ 0,4^-1

5)   (1/3)^m < (1/3)ⁿ

6)   (2/7) ^m ˃ (2/7) ⁿ

 

➢Як розташовані графіки функцій у=3^х та у=(1/3)^х ?

(Графіки розташовані симетрично відносно осі OY);

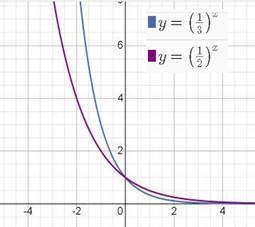
➢Чим відрізняються властивості і графіки функцій у=(1/2)^х і у=(1/3)^х ?

(Вони мають однакові властивості, функція у=(1/2)^х спадає більш швидше).

 

 

V.         Систематизація вивченого матеріалу.

➢Вказати область визначення показникової функції.

-         Область визначення показникової функції – множина R

дійсних чисел, бо степінь а^х, де а˃0, визначений для всіх х є R.

➢Вказати область значень показникової функції.

-         Множина значень показникової ф-ції – множина всіх додатних дійсних чисел.

➢На якій множині показникова функції є зростаючою?

-         Показникова ф-ція у=а^х є зростаючою на множині дійсних чисел, якщо а ˃ 1.

➢На якій множині показникова функції є спадаючою?

-         Показникова функції у=а^х є спадною на множині дійсних чисел, якщо 0<а<1.

➢Якщо х=0, то у = а⁰ = 1

➢Якщо х˃0, то у˃1, якщо а˃1, у<1, якщо 0<а<1

➢Якщо х<0, то у<1, якщо а˃1, у˃1, якщо 0<а<1

➢Як називаються графік показникової функції?

- Графіком показникової ф-ції є крива, яка називається експонентою.

А зараз в робочих зошитах у вигляді таблиці запишемо властивості показникової ф-ції:

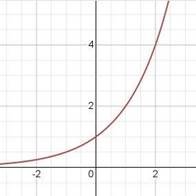
 Показникова функція  у=а^х, а˃0, а≠1, 

                якщо а˃1                                         якщо 0<а<1

                        

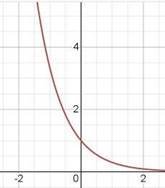
1. D(у) = R	1. D(у) = R
2. E(у)=(0;+ ∞)	2. Е(у)=(0;+ ∞)
3. Зростає х1˃х2=˃ ах1˃ах2	3. Спадає х1˃х2=˃ ах1<ах2
4. Якщо х=0, то у=1	4. Якщо х=0, то у=1
5. Якщо х<0, то у<1	5. Якщо х<0, то у ˃1
6. Якщо х˃0, то у˃1	6. Якщо х˃0, то у<1

VI.     Розв’язати вправи (вправи записані на дошці)

1) Порівняйте:

a.                 20,7 ˃ 22/5

b.                 √5⁰ ˃ √5-1 

c.                 (5/7)³ ˃ (5/7)⁵ 

d.                 6,5² ˃ 6,5^-2 2) Які з функцій зростаючі, а які спадаючі?

a.     у=3,2^х

b.    у=0,3^х

c.     у=(1/8)^х

d.    (2-√2) ² ˃ (2-√2)³

e.     у= π ^х

3) Порівняйте а з 1, якщо:

a.     а^1/2  ˃ а^1/3; а ˃1

b.    а⁵ < а³; 0<а<1

c.     а^-2 ˃ а^-3; а ˃1

VIІ.  Підсумок уроку.

VІІІ. Домашнє завдання: завдання Шкіль, стор. 201, зап. 1-13 (частина-усно; частина – письмово вибірково), в зошит записати 7 запитань.