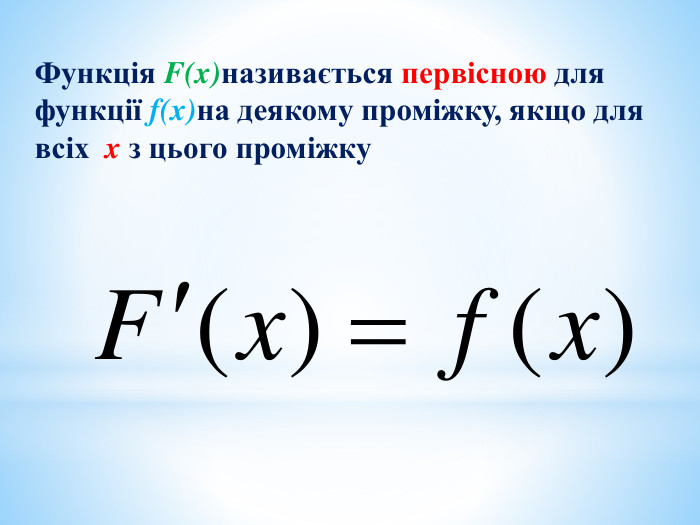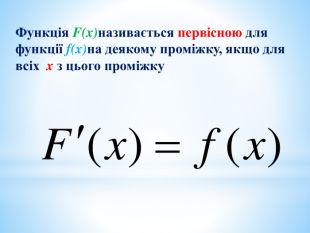Презентація "Інтеграл. Площа криволінійної трапеції"
Про матеріал
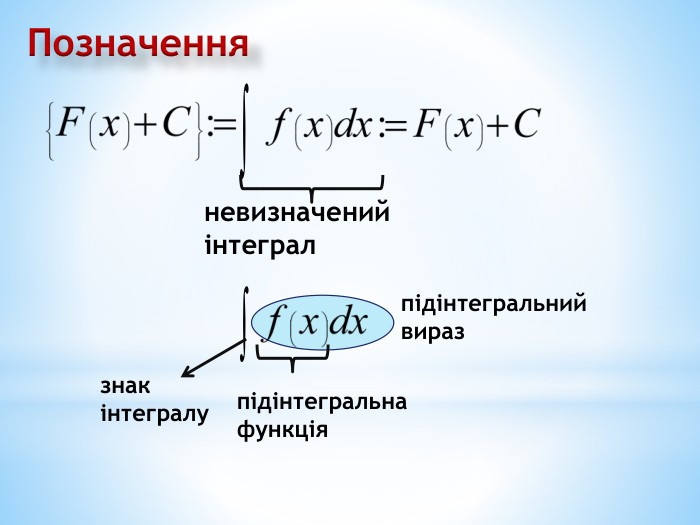
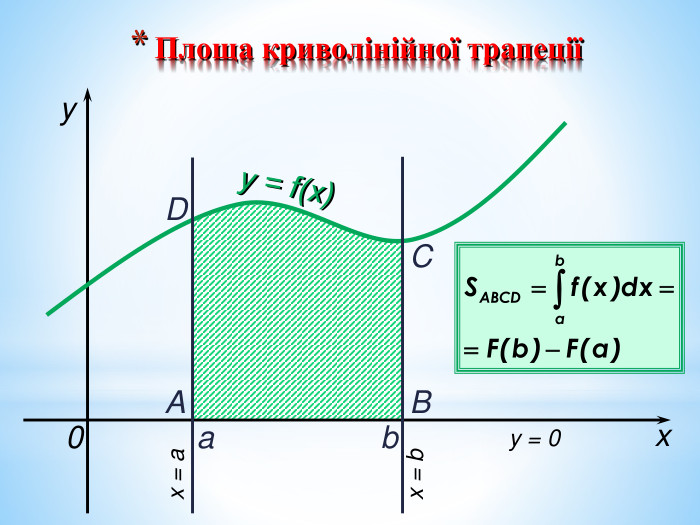
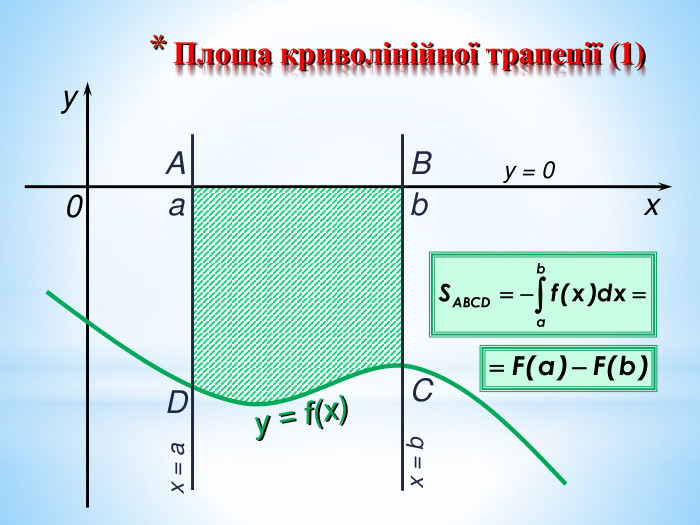
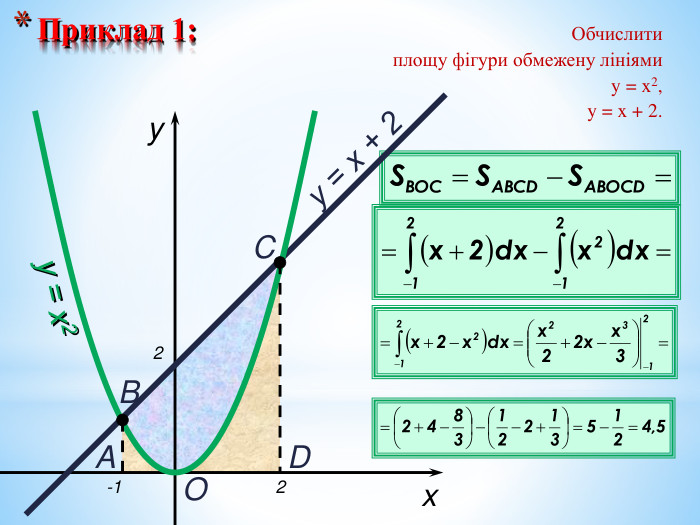
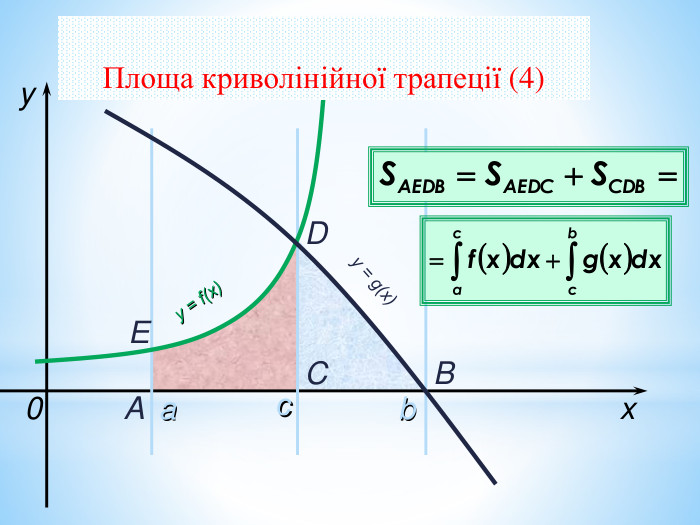
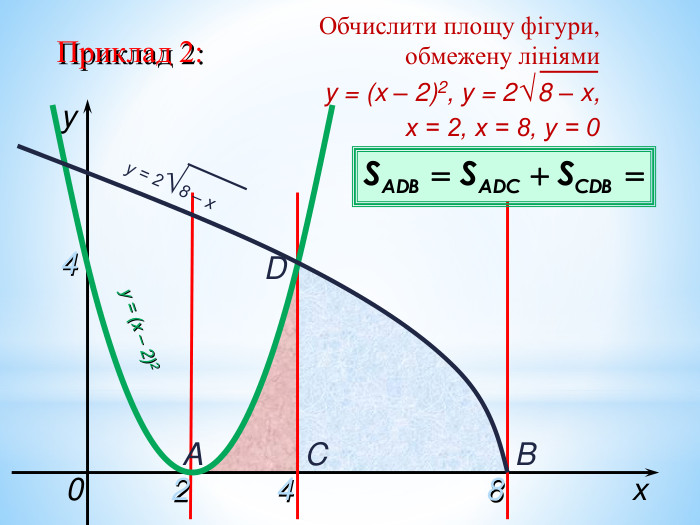
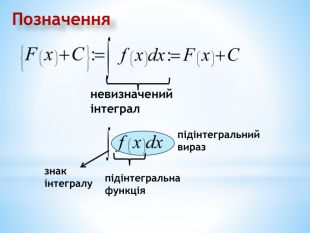
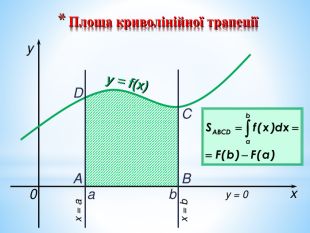
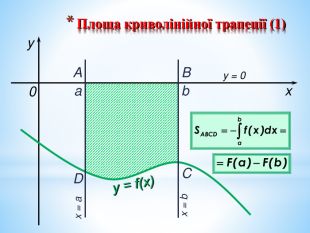
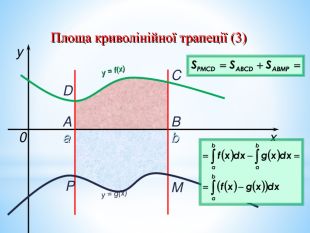
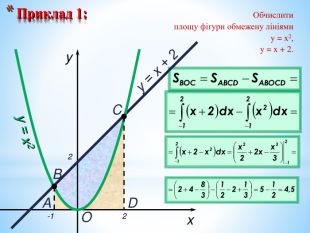
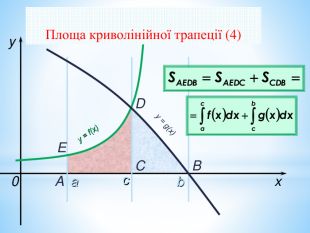
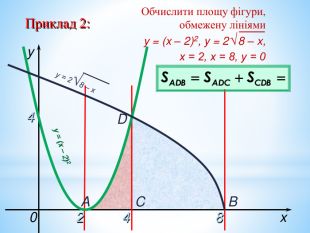
Презентація на повторення теми "Інтеграл. Площа криволінійної трапеції".
Може бути використана при узагальненні поняття інтеграла, зокрема, обчислення площ криволінійних трапецій. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку