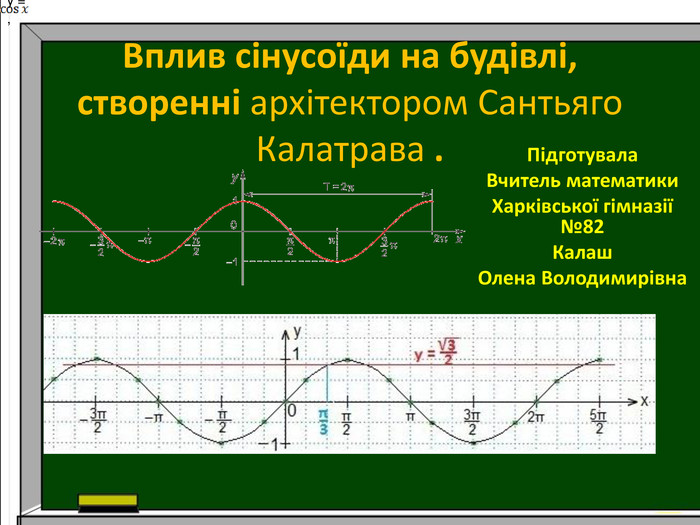
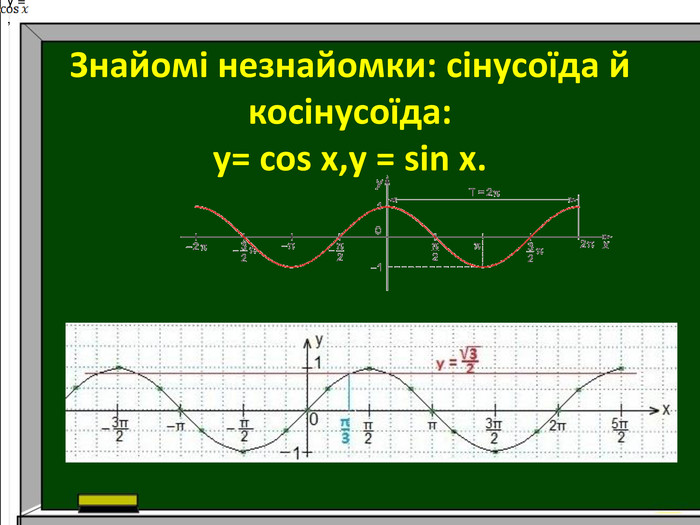
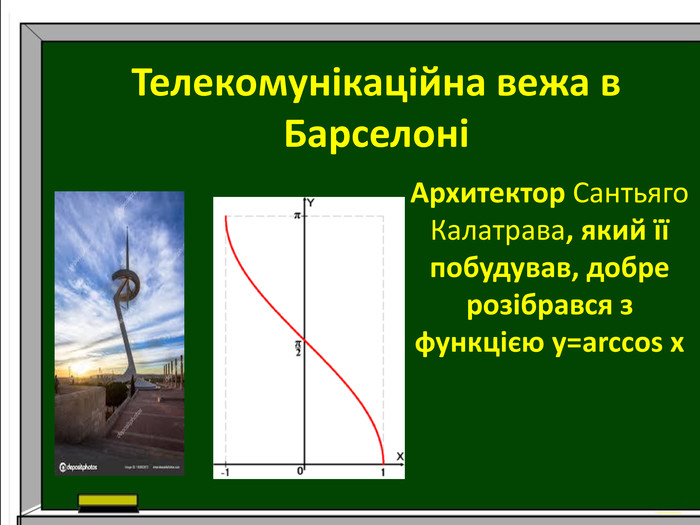
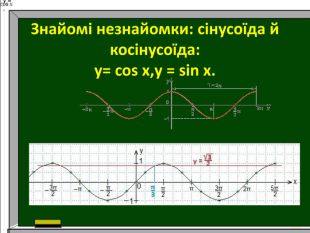
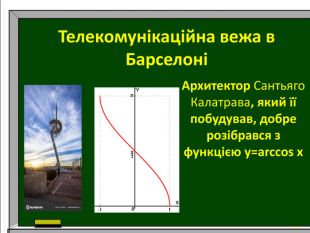
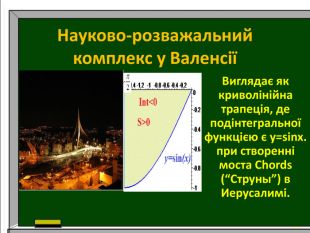
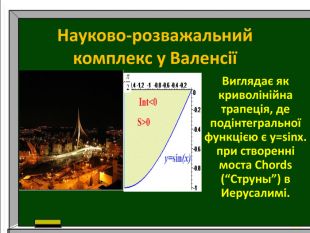
Презентація до уроку алгебри в 10 класі. Тема. "Використання графіків тригонометричних функцій в архітектурі."
Про матеріал
Дослідження: використання графіків тригонометричних функцій в архітектурі. Розвивати математичну грамотність, навички самоаналізу, увагу, пам`ять, цікавість до математики.
Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку