Презентація до уроку геометрії. 9 клас. Тема "Правильні многокутники та їх властивості"

Правильні многокутники

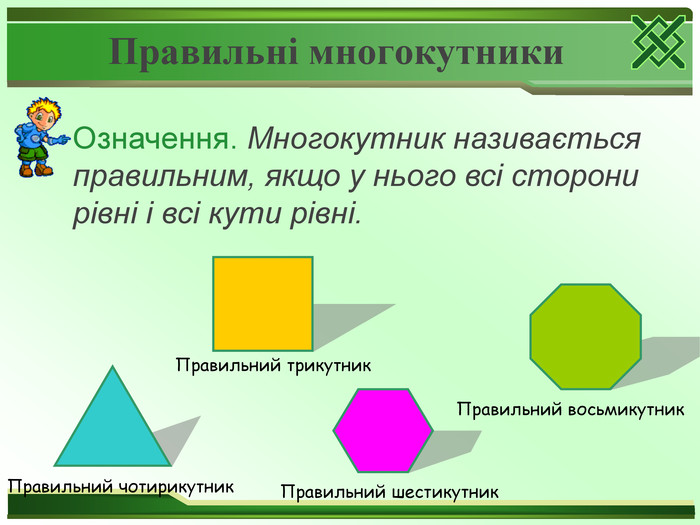
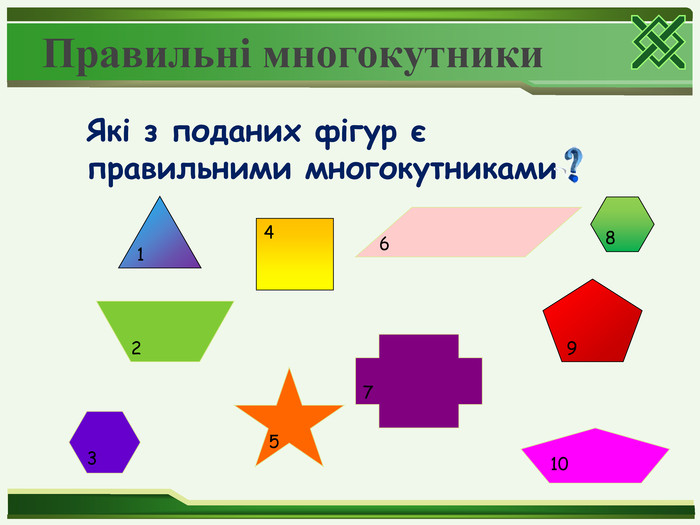
Мета уроку сформувати поняття правильного многокутника, центрального кута правильного многокутника 

Девіз уроку Геометрія - наше велике творіння, яке нас самих захоплює.                                                                Ле Корбюзьє, французький архітектор   

Правила успішності Будьте               УВАЖНИМИ                              ДИСЦИПЛІНОВАНИМИ                            АКТИВНИМИ                              ЧЕСНИМИ                            АЗАРТНИМИ     

Вправа «Мікрофон» Яку фігуру називають многокутником? Які многокутники вам відомі? Який многокутник є найпростішим? Чому дорівнює сума кутів трикутника? Який це опуклий многокутник? А не опуклий?

Розв'язати усно 1. Знайдiть суму внутрiшнiх кутiв: 1) трикутника; 2) чотирикутника; 3) шестикутника; 4) десятикутника. 2. У многокутнику всi кути рiвнi. Знайдiть кiлькiсть кутiв многокутника, якщо зовнiшнiй кут дорiвнює 30°. 3. Яка точка є центром кола, описаного навколо прямокутника? 4. Чи можна вписати коло в ромб? Якщо вiдповiдь позитивна, то вкажiть, де знаходиться центр цього кола?

А чи знаєш ти… Фігури, що мають рівні сторони та кути,  здавна зачаровували людину досконалістю форми і таємничістю, яка завжди  супроводжує досконалість. Такі фігури обожнювали, приписуючи їм магічні та навіть цілющі властивості.

Вправа «Мікрофон» Чому дорівнює сума кутів опуклого n – кутника? Яке коло називають описаним навколо многокутника? Яке коло називають вписаним в многокутник?

Правильні многокутники Означення. Многокутник називається правильним, якщо у нього всі сторони рівні і всі кути рівні. Правильний восьмикутник Правильний шестикутник Правильний трикутник Правильний чотирикутник

Правильні многокутники Які з поданих фігур є правильними многокутниками 1 2 3 4 5 6 7 8 9 10

Градусна міра кута

Центральний кут

Для чого вивчати правильні многокутники? Правильні многокутники — це абстрактні поняття, створені науковцями. У природі абсолютно правильних многокутників не існує. Трапляються об’єкти у формі майже правильних многокутників. Наприклад, бджоли роблять стільники у формі майже правильних шестикутників. 

Для чого вивчати правильні многокутники? Квіти багатьох рослин ростуть так, що кінчики їх пелюсток розташовані у вершинах правильних многокутників, а кінчики сніжинок розташовані у вершинах правильних шестикутників. Форми майже правильних многокутників мають грані деяких кристалів. Наприклад, грані кристалів кухонної солі — квадрати, грані кристалів алмаза — правильні трикутники.

Для чого вивчати правильні многокутники? Правильні многокутники зустрічаються і в багатьох виробах (голівках болтів і гайок, пельменницях).

Для чого вивчати правильні многокутники? В архітектурі часто можна побачити будови, що мають форми правильних многокутників або їх частин. Особливо часто з правильними многокутниками мають справу паркетники, плиточники, архітектори. У деяких палацах, залах настеляють паркет з кількох правильних многокутників: правильних трикутників і шестикутників, квадратів і правильних восьмикутників тощо.

Розв'язати Обчисліть кут правильного n-кутника, якщо: 1) n = 5; 2) n = 12; 3) n = 18. Робота в парі

Розв'язати Знайдіть центральний кут правильного n-кутника, якщо: 1) n = 20; 2) n = 24; 3) n = 10. Колективно

РОЗВ'ЯЗАТИ Знайдіть кут правильного n-кутника, якщо його зовнішній кут дорівнює: 1) 60°; 2) 26°; 3) 34°. Самостійно

РОЗВ'ЯЗАТИ Знайдіть кількість сторін правильного n-кутника, якщо його кут дорівнює: 1) 135°; 2) 150°; 3) 140°. Робота в групі

«Вірю – не вірю» 1. Будь-який  правильний многокутник є  випуклим    2.Будь-який  випуклий многокутник є  правильним?    3.Многокутник є правильним, якщо він випуклий і всі його сторони рівні.   

«Вірю – не вірю»  4.Трикутник є правильним, якщо  всі його кути рівні    5.Будь-який рівносторонній трикутник  є правильним.     6.Будь-який  чотирикутник з рівними сторонами є правильним.     7. Будь-який  правильний  чотирикутник  є квадратом.

ЦЕ ЦІКАВО Правильні многокутники                          З часів Піфагора відомі вони.                            У них рівні сторони, рівні кути.  Зустрінемо в орнаментах і на паркетах,                      І у віршах відомих поетів.  І навіть бджоли з ними працюють,    І мед для здоров’я нам пропонують!

Домашнє завдання Розділ V, § 17 – опрацювати, № 609 і задача: Знайдіть кількість сторін правильного n-кутника, якщо його кут дорівнює: 1) 135°; 2) 150°; 3) 140°.

Використані джерела: А.П. Ершова, В.В. Голобородько… «Геометрія-9» , «Гімназія», 2017 рік. А.С. Зоря, С.М. Кіро  «Про математику і математиків». Київ «Радянська школа», 1981    О.В. Джерело: http://5fan.ru/wievjob.php?id=54395. Інтернет ресурс.