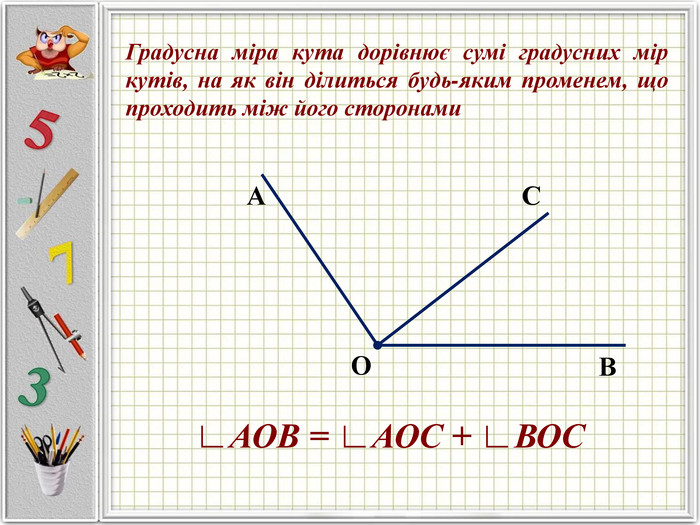
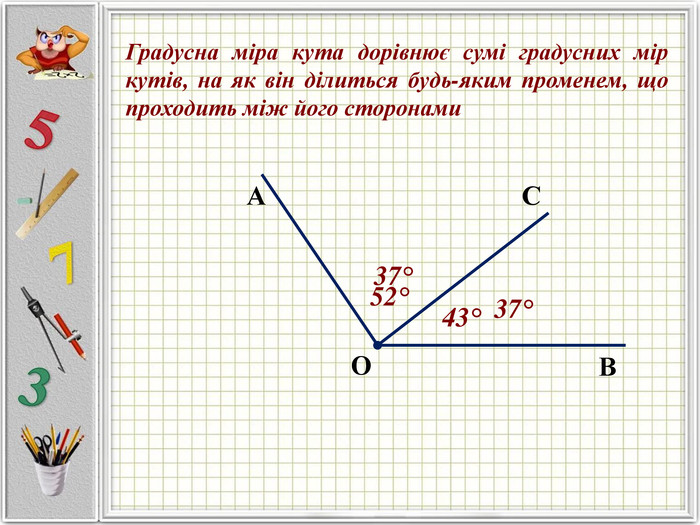
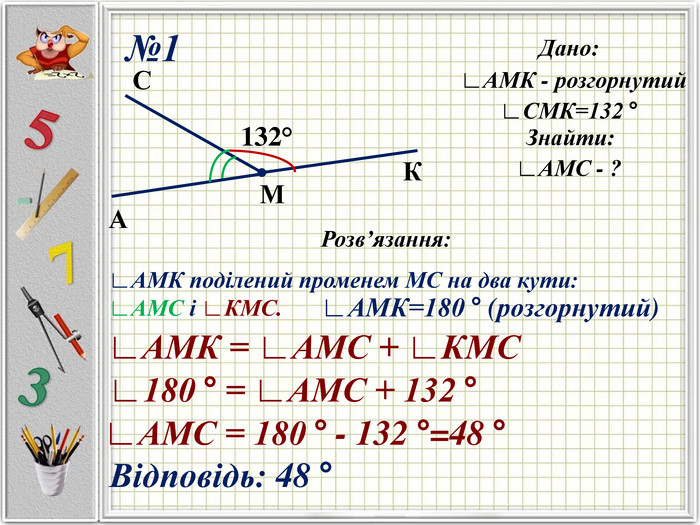
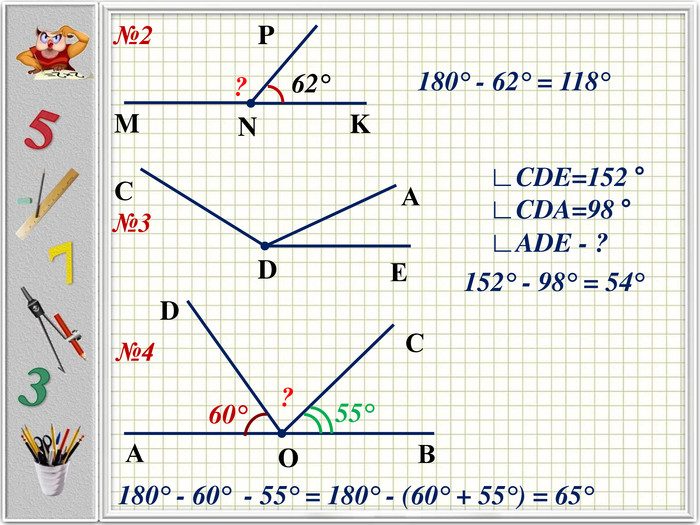
Презентація до уроку "Кути. Розв'язування задач. 5 клас"
Про матеріал
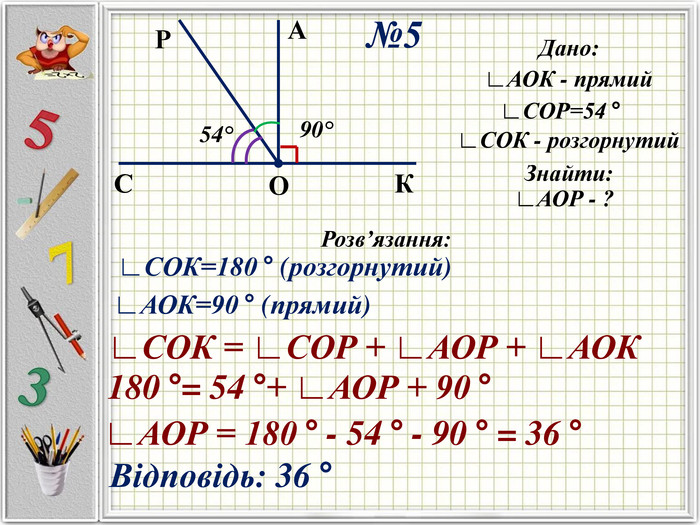
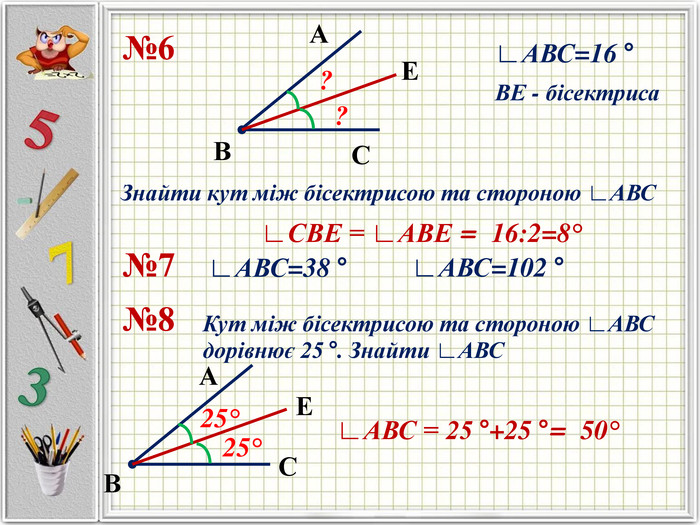
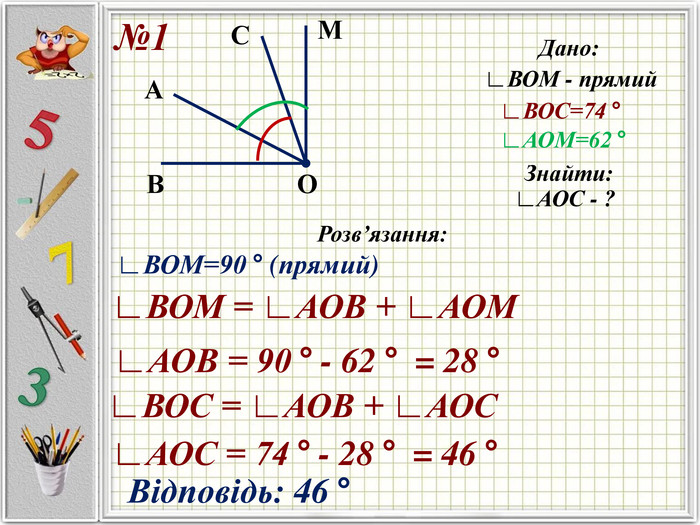
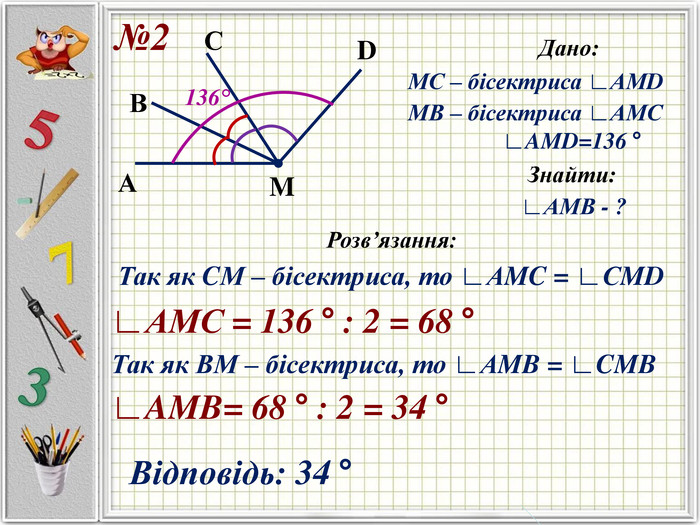
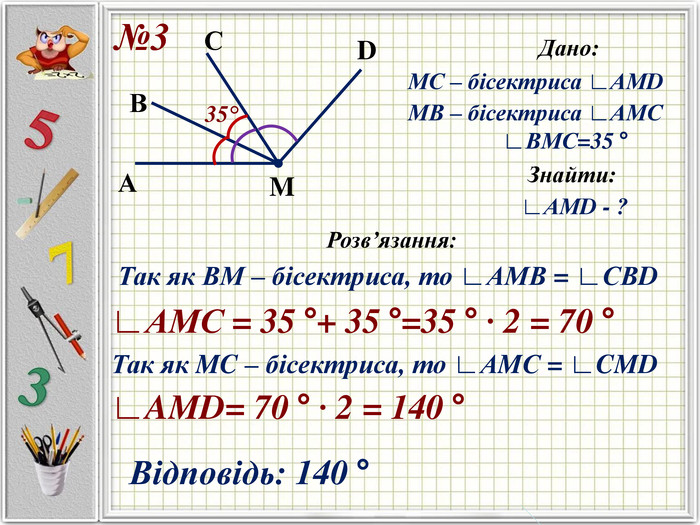
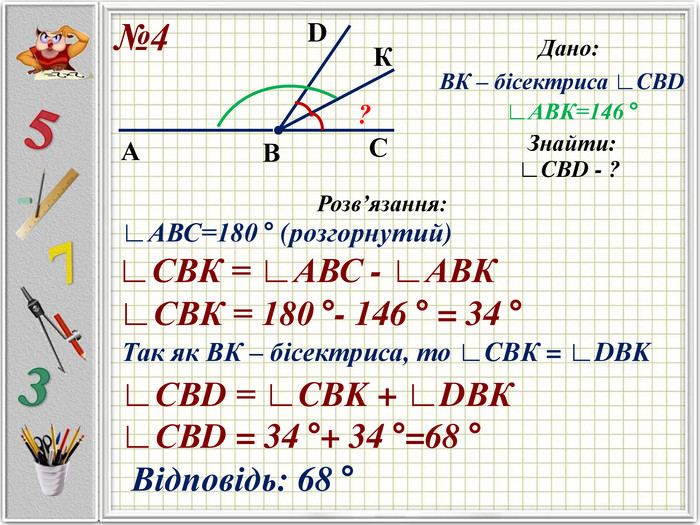
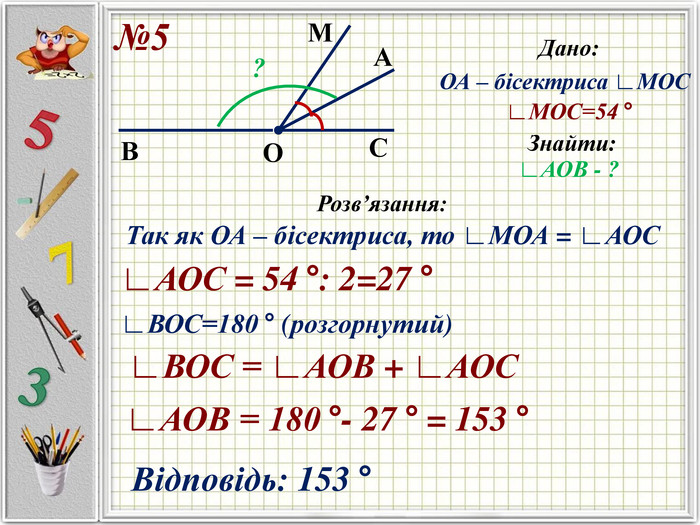
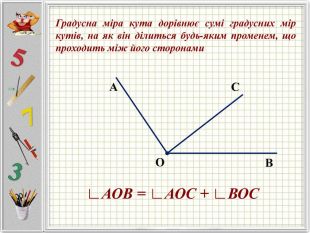
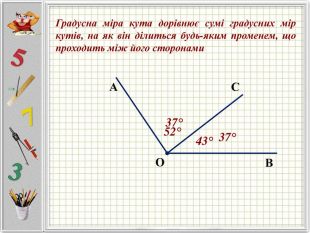
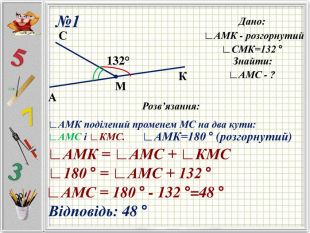
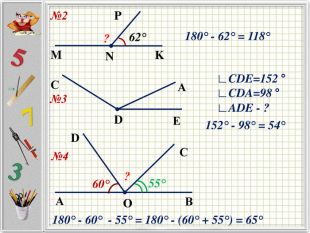
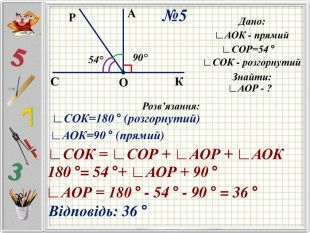
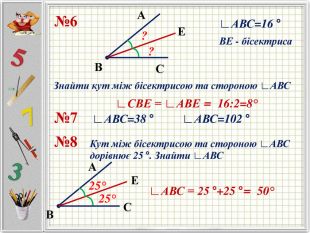
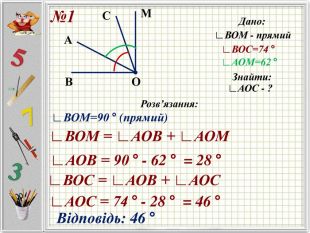
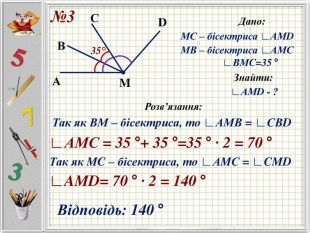
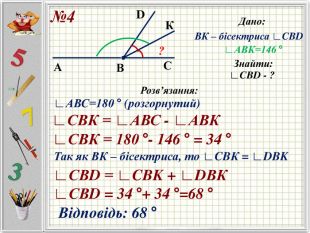
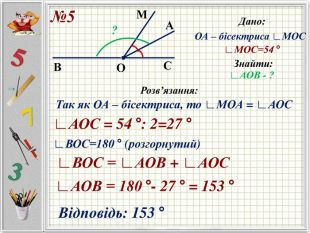
Презентацію можна використати під час другого уроку при вивченні еми "Кути" у 5-му класі. В даній розробці розглянуті задачі різного рівня складності, на використання поняття бісектриси кута, видів кутів, властивості вимірювання кутів. Можна викоритати презентацію під час дистанційного навчання, адже кожна задача має детальне розв'язання для того, щоб учні мали можливость вдома ще раз опрацювати дану тему. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку