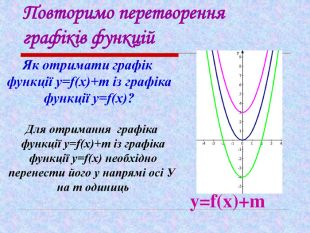
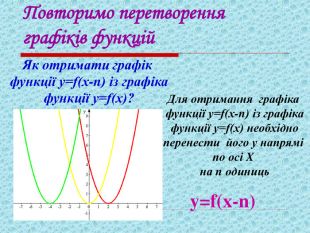
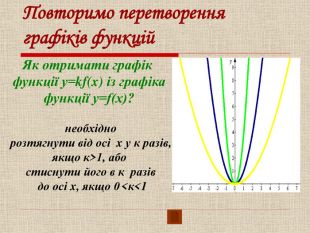
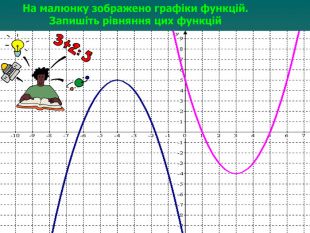
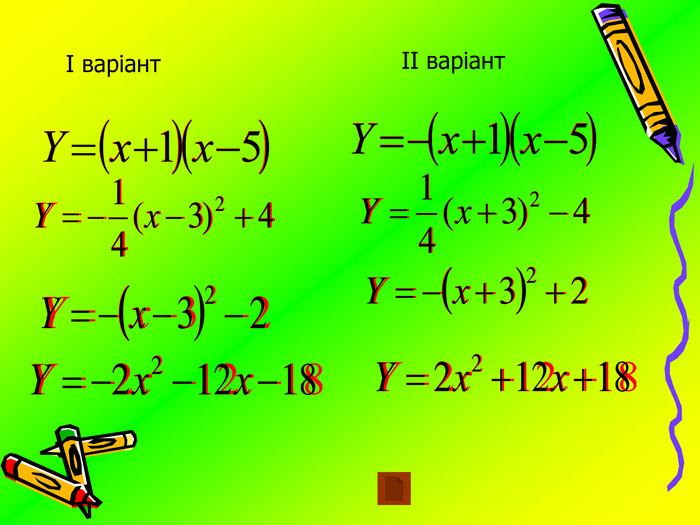Презентація до уроку "Квадратична функція"
Про матеріал
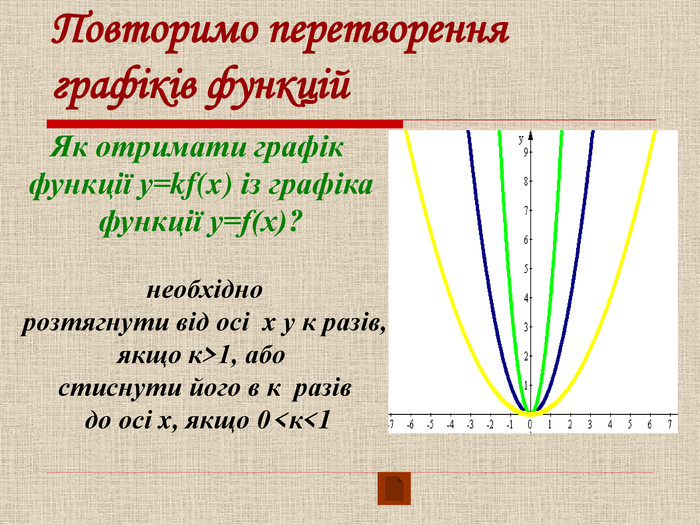
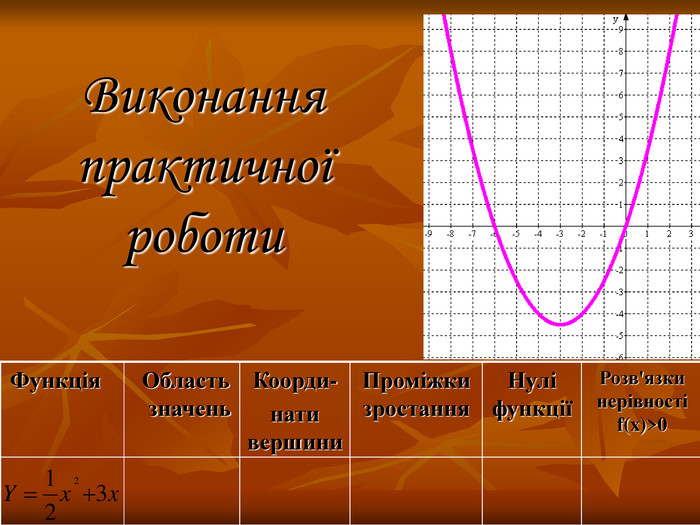
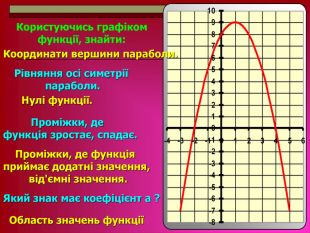
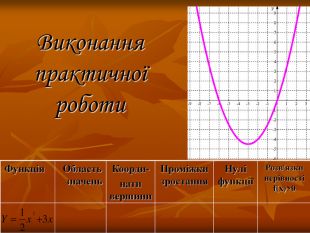
Урок систематизації та узагальнення знань, умінь та навичок учнів з теми:
«Квадратична функція та її властивості». Мета: оцінити рівень теоретичної підготовки учнів i вміння застосовувати набуті знання з теми «Квадратична функція». Діагностика рівня підготовки учнів до подальшого вивчення навчального матеріалу, пов’язаного з поняттям функції у старших класах. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку