Збірник завдань для контролю знаньз алгебри та початків аналізу 10 клас профільний рівень
збірник завдань для контролю знань з алгебри та почтаків аналузу для 10 класу профільний рівень
завдання для самостійних та контрольних робіт, що охоплюють усі теми
Департамент освіти і науки Київської обласної державної адміністрації
Київський обласний інститут післядипломної освіти педагогічних кадрів
Відділ освіти Богуславської районної державної адміністрації
Богуславська академічний ліцей № 1
Богуславської районної ради Київської області
Галина Тропотяга
Алгебра та початки аналізу
10 клас профільний рівень
Збірник завдань для контролю знань
Богуслав
![]() 2020
2020
Тропотяга Г. О. Алгебра та початки аналізу. 10 клас. Профільний рівень: Збірник завдань для контролю знань/ Г. О. Тропотяга. – Богуслав, 2020 – 43 с.
Посібник відповідає чинній програмі з математики для 10 класу загальноосвітніх навчальних закладів (профільний рівень), містить розробки завдань самостійних та контрольних робіт.
Матеріал, наведений у збірнику, об’єднаний у 6 тем. Кожна тема містить самостійні та контрольні роботи у двох варіантах.
Адресовано вчителям математики загальноосвітніх навчальних закладів, учням 10 класу.
![]()
ЗМІСТ
Діагностична контрольна робота
І. ФУНКЦІЇ, МНОГОЧЛЕНИ, РІВНЯННЯ І НЕРІВНОСТІ
Тема 1. Числові множини. Числові функції та їх властивості
Тема 2. Рівняння та нерівності
Тема 4. Ірраціональні рівняння та нерівності
Тема 5. Властивості та графіки тригонометричних функцій
Тема 6. Співвідношення між тригонометричними функціями одного аргументу
IV. ТРИГОНОМЕТРИЧНІ РІВНЯННЯ І НЕРІВНОСТІ
Тема 7. Обернені тригонометричні функції. Основні способи розв’язування тригонометричних рівнянь
Тема 8. Тригонометричні нерівності
V. ГРАНИЦЯ ТА НЕПЕРЕРВНІСТЬ ФУНКЦІЇ. ПОХІДНА ТА її ЗАСТОСУВАННЯ
Тема 10. Дослідження функцій за допомогою похідної
Тема 11. Застосування похідної до розв’язування задач, зокрема прикладного змісту
VI. ПОВТОРЕННЯ, УЗАГАЛЬНЕННЯ ТА СИСТЕМАТИЗАЦІЯ НАВЧАЛЬНОГО МАТЕРІАЛУ, РОЗВ’ЯЗУВАННЯ ЗАДАЧ
ВСТУП
Збірник містить повну добірку самостійних та контрольних робіт з курсу алгебри та початків аналізу для 10 класу профільного рівня; складений відповідно до вимог чинної програми.
Контрольні роботи розраховані на один урок, самостійні роботи – на 25-40 хвилин, у залежності від теми та рівня підготовки учнів.
Матеріал, наведений у збірнику, об’єднаний у 6 тем, відповідно до навчальної програми 10 класу профільного рівня: «Функції, многочлени, рівняння і нерівності», «Степенева функція», «Тригонометричні функції», «Тригонометричні рівняння і нерівності», «Границя та неперервність функції. Похідна та її застосування», «Повторення, узагальнення та систематизація навчального матеріалу». Кожна тема містить самостійні та контрольні роботи у двох варіантах.
Об’єм самостійних та контрольних робіт є орієнтовним, учитель може варіювати його, виходячи з рівня підготовки учнів та особливостей психолого-педагогічної характеристики класу.
Зміст і структура запропонованого дидактичного матеріалу дозволяє здійснити диференційований контроль навчальних досягнень та об’єктивно оцінити рівень засвоєння учнями програмового матеріалу, підготувати учнів до олімпіад та ЗНО з математики.
Діагностична контрольна робота
Варіант 1
-
Яке з чисел є розв’язком нерівності
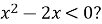
|
а) -1; |
б) 0; |
в) 1; |
г) 2. |
- Яка з наведених систем нерівностей не має розв’язків?
|
а) |
б) |
в) |
г) |
-
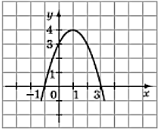 На рисунку зображено графік функції
На рисунку зображено графік функції 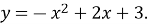 Укажіть найбільше значення функції.
Укажіть найбільше значення функції.
|
а) 1; |
б) 3; |
в) 2; |
г) 4. |
-
Розв’яжіть нерівність
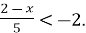
- Вкладник поклав до банку 15000 грн. під 10% річних. Яку суму він отримає через 2 роки?
-
Розв’яжіть систему рівнянь
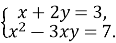
-
Знайдіть цілі розв’язки системи нерівностей
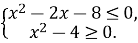
Варіант 2
-
Оцініть значення виразу
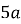 , якщо
, якщо 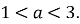
|
а) |
б) |
в) |
г) |
- Розв’язком якої з наведених нерівностей є число 1?
|
а) |
б) |
|
в) |
г) |
-
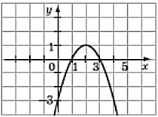 На рисунку зображено графік функції
На рисунку зображено графік функції  Розв’яжіть нерівність
Розв’яжіть нерівність 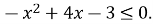
|
а) |
б) |
|
в) |
г) |
-
Розв’яжіть нерівність
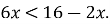
- Вартість дитячого велосипеда зросла з 260 грн. до 312 грн. На скільки відсотків зросла ціна?
-
Розв’яжіть систему рівнянь
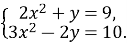
-
Знайдіть область визначення функції
І. ФУНКЦІЇ, МНОГОЧЛЕНИ, РІВНЯННЯ І НЕРІВНОСТІ
Тема 1. Числові множини. Числові функції та їх властивості
Під множиною в математиці розуміють зібрання, сукупність будь-яких предметів, об’єктів, об’єднаних між собою деякою загальною для них усіх ознакою. Предмети (об’єкти), з яких складається множина, називаються її елементами. Для позначення множин, застосовують великі букви A, В, С..., для позначення елементів — малі а, b, с... Той факт, що елемент а є елементом множини А, записують так: ![]() (читається: а є елементом множини А, або а належить А, або а міститься в А, або А містить а). Якщо елемент x не є елементом множини А, то це записується так:
(читається: а є елементом множини А, або а належить А, або а міститься в А, або А містить а). Якщо елемент x не є елементом множини А, то це записується так: ![]() (читається: x не є елементом множини А, або x не належить А, або x не міститься в А, або А не містить х).
(читається: x не є елементом множини А, або x не належить А, або x не міститься в А, або А не містить х).
Множину можна задати перерахуванням її елементів. Наприклад, якщо A — множина дільників числа 30, то ![]() . Запис
. Запис ![]() означає, що множина A складається із всіх чисел x, що задовольняють нерівності
означає, що множина A складається із всіх чисел x, що задовольняють нерівності ![]() . Умова «x – розв’язок нерівності
. Умова «x – розв’язок нерівності ![]() » називається характеристичною властивістю множини A.
» називається характеристичною властивістю множини A.
Множина, що має певну кількість елементів називається скінченною. Якщо множина має нескінчену кількість елементів, її називають нескінченною множиною. Множину, яка не має жодного елемента, називають порожньою і позначають так ![]() .
.
Запис ![]() означає, що множина А називається підмножиною множини В, тобто кожний елемент множини А є елементом множини В.
означає, що множина А називається підмножиною множини В, тобто кожний елемент множини А є елементом множини В.
Загальноприйняті позначення деяких числових множин.
N – множина всіх натуральних чисел;
Z – множина всіх цілих чисел;
Q – множина всіх раціональних чисел;
R – множина всіх дійсних чисел.
Перерізом множин А і В є множина, що складається з елементів, які належать кожній із множин А і В. Позначається : ![]() (AB – добуток множин).
(AB – добуток множин).
Об’єднанням множин А і В є множина, що складається з елементів, які належать хоча б одній із множин А або В. Позначається: ![]() (AB – сума множин).
(AB – сума множин).
Різницею множин А і В є множина, що складається з усіх елементів множини А, які не належать множині В. Позначається: ![]() (A-B – різниця множин).
(A-B – різниця множин).
Між множинами А і В установлено взаємно однозначну відповідність, якщо кожному елементу ![]() поставлено у відповідність один елемент
поставлено у відповідність один елемент ![]() , і при цьому кожний елемент b з B відповідає одному й тільки одному елементу a з A.
, і при цьому кожний елемент b з B відповідає одному й тільки одному елементу a з A.
Множини А і В називаються еквівалентними, якщо між їхніми елементами можна встановити взаємно однозначну відповідність. Говорять, що множини А і В мають однакову потужність.
Нескінченна множина називається зліченною, якщо вона еквівалентна множині натуральних чисел. Будь-яка нескінченна підмножина A натурального ряду чисел N зліченна.
Незліченні множини – нескінченні множини, елементи яких не можна пронумерувати. Найпростіший приклад – множина всіх точок відрізка ![]() Такі множини називаються континуальними. Ірраціональні числа утворюють континуальні множини. Рахункова і континуальна множини не є еквівалентними.
Такі множини називаються континуальними. Ірраціональні числа утворюють континуальні множини. Рахункова і континуальна множини не є еквівалентними.
Числовою функцією з областю визначення D називається залежність, при якій кожному числу х із множини D (області визначення) ставиться у відповідність єдине число у. Записують цю відповідність так: ![]() .
.
Позначення і терміни: ![]() – область визначення,
– область визначення, ![]() – область значень, х – аргумент (незалежна змінна), у – функція (залежна змінна),
– область значень, х – аргумент (незалежна змінна), у – функція (залежна змінна), ![]() – функція,
– функція, ![]() – значення функції
– значення функції ![]() у точці
у точці ![]() .
.
Графіком функції ![]() називається множина всіх точок координатної площини з координатами
називається множина всіх точок координатної площини з координатами![]() , де перша координата х «пробігає» всю область визначення функції, а друга координата – це відповідне значення функції
, де перша координата х «пробігає» всю область визначення функції, а друга координата – це відповідне значення функції ![]() у точці х.
у точці х.
Функцію ![]() називають зростаючою на деякому проміжку області визначення функції, якщо для будь-яких двох точок
називають зростаючою на деякому проміжку області визначення функції, якщо для будь-яких двох точок ![]() і
і ![]() цього проміжка з нерівності
цього проміжка з нерівності ![]() випливає нерівність
випливає нерівність![]() Якщо для кожних двох точок
Якщо для кожних двох точок ![]() і
і ![]() даного проміжка з нерівності
даного проміжка з нерівності ![]() випливає нерівність
випливає нерівність![]() , то функцію
, то функцію ![]() називають спадною на даному проміжку.
називають спадною на даному проміжку.
Означення. Монотонною називається функція, яка зростає (або спадає) на всій області визначення.
Якщо з нерівності ![]() випливає нерівність
випливає нерівність![]() , то функцію називають неспадною.
, то функцію називають неспадною.
Якщо з нерівності ![]() випливає нерівність
випливає нерівність![]() , то функцію називають незростаючою.
, то функцію називають незростаючою.
Функція ![]() парна, якщо
парна, якщо ![]() для всіх х з області визначення. Графік парної функції симетричний відносно осі Оу.
для всіх х з області визначення. Графік парної функції симетричний відносно осі Оу.
Функція ![]() непарна, якщо
непарна, якщо ![]() для всіх х з області визначення. Графік непарної функції симетричний відносно початку координат – точки
для всіх х з області визначення. Графік непарної функції симетричний відносно початку координат – точки ![]()
Значення аргументу, при яких функція дорівнює 0, називаються нулями функції. Графік функції при таких значеннях аргументу перетинає вісь Ox.
♦ Схема розв’язування рівнянь та нерівностей, що містять знак модуля
-
а)
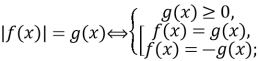
б) 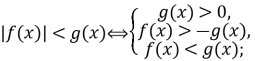
в) 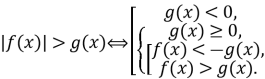
-
а)
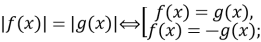
або ![]()
б) ![]()
- Метод інтервалів для виразів, що містять знак модуля
Алгоритм перетворення виразу, що містить декілька знаків модуля:
- Прирівняйте кожний вираз, що стоїть під знаком модуля, до нуля і розв’яжіть отримані рівняння.
- Розмістіть отримані числа на координатній прямій, розбивши її таким чином на інтервали.
- Дослідіть знак кожного виразу, що стоїть під знаком модуля, на кожному з інтервалів.
-
Знайдіть розв’язок рівняння чи нерівності на кожному з інтервалів, враховуючи те, що:
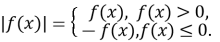
Оскільки ![]() , то граничні точки проміжків будуть враховані двічі.
, то граничні точки проміжків будуть враховані двічі.
Самостійна робота 1
Множини, операції над множинами. Функції, властивості функцій
|
Варіант 1 |
Варіант 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
1) |
|
|
|
|
|
Самостійна робота 2
Перетворення графіків функцій. Оборотна та обернена функція
|
Варіант 1 |
Варіант 2 |
|
|
|
|
|
|
|
|
1)
2) |
1)
2) |
|
|
|
|
|
Контрольна робота № 1
«Числові множини. Числові функції та їх властивості»
Варіант 1
- Знайдіть перетин і об’єднання множин А і В, де А – множина дільників числа 12, В – множина дільників числа 30.
-
Задайте функцію, обернену до функції
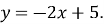
-
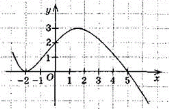 Функцію задано графічно. Укажіть:
Функцію задано графічно. Укажіть:
1) нулі функції;
2) проміжки зростання та спадання;
3) проміжки знакосталості.
- Дослідіть функцію на парність:
1) ![]() 2)
2) ![]() ; 3)
; 3) ![]() .
.
- Побудувати графік функції:
![]() 2)
2) ![]()
Варіант 2
- Знайдіть перетин і об’єднання множин А і В, де А – множина дільників числа 18, В – множина дільників числа 24.
-
Задайте функцію, обернену до функції
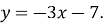
-
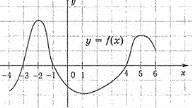 Функцію задано графічно. Укажіть:
Функцію задано графічно. Укажіть:
1) нулі функції;
2) проміжки зростання та спадання;
3) проміжки знакосталості.
- Дослідіть функцію на парність:
1) ![]() 2)
2) ![]()
3) ![]()
- Побудувати графік функції:
1) ![]() ; 2)
; 2) ![]() .
.
Тема 2. Рівняння та нерівності
Самостійна робота 1
Розв’язування рівнянь та нерівностей
|
Варіант 1 |
Варіант 2 |
|
|
|
1)
2)
3) |
1)
2)
3) |
|
|
|
1)
2)
3) |
1)
2)
3) |
Самостійна робота 2
Розв’язування рівнянь та нерівностей, що містять знак модуля
|
Варіант 1 |
Варіант 2 |
|
|
||
|
2) |
|
|
|
||
|
1)
2) |
1)
2) |
|
|
||
|
|
|
|
|
4. При яких значеннях параметра b рівняння |
4. При яких значеннях параметра a рівняння має два різні корені. |
|
Контрольна робота № 2
«Рівняння та нерівності»
|
Варіант 1 |
Варіант 2 |
|
|
|
1)
2) |
1)
2) |
|
|
|
1)
2) |
|
3. При якому значенні параметра a остача від ділення многочлена |
3. При якому значенні параметра a остача від ділення многочлена |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ІІ. СТЕПЕНЕВА ФУНКЦІЯ
Тема 3. Степенева функція
♦ Корінь n–го степеня
Означення. Коренем n–го степеня з числа a називається таке число, n–ий степінь якого дорівнює a (n – натуральне число).
Прийнято такий запис: ![]() – показник кореня, a – підкореневий вираз.
– показник кореня, a – підкореневий вираз.
Арифметичний корінь – невід’ємне значення кореня.
При ![]() – позначення арифметичного значення кореня.
– позначення арифметичного значення кореня.
![]() :
:
-
при
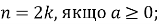
-
при
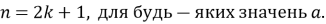
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
♦ Властивості кореня n – го степеня
|
|
|
|
|
|
|
|
|
♦ Наслідки
-
Винесення множника з-під знака кореня
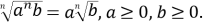 Корінь непарного степеня
Корінь непарного степеня 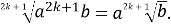
Корінь парного степеня ![]()
-
Внесення множника під знак кореня
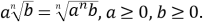
Корінь непарного степеня ![]()
Корінь парного степеня
![]()
-
Якщо
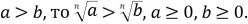
♦ Розв’язування ірраціональних рівнянь та нерівностей
Рівняння або нерівність називаються ірраціональними, якщо невідоме знаходиться під знаком кореня.
- Рівняння:
а) ![]()
б) ![]()
- Нерівності:
а) 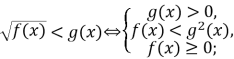
б) 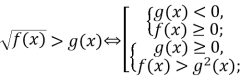
в) ![]()
г) ![]()
Самостійна робота 1
Перетворення виразів n–го степеня
|
Варіант 1 |
Варіант 2 |
|
1. Знайдіть значення виразу: |
|
|
1)
2)
3)
4) |
1)
2)
3)
4) |
|
2. Розв’яжіть рівняння: |
|
|
2)
3)
4) |
2)
3)
4) |
|
3. Спростіть вираз: |
|
|
1)
2) |
1)
2) |
|
4. Обчисліть: |
|
|
|
|
|
5. Побудувати графік функції: |
|
|
|
|
Самостійна робота 2
Степінь із раціональним показником
|
Варіант 1 |
Варіант 2 |
|
1.Знайдіть значення виразу: |
|
|
1)
2)
3)
4) |
1)
2)
3)
4) |
|
2. Спростіть вираз: |
|
|
1)
2)
3)
4) |
1)
2)
3)
4) |
|
3. Скоротіть дріб: |
|
|
1)
2)
3) |
1)
2)
3) |
Контрольна робота № 3
«Степенева функція»
|
Варіант 1 |
Варіант 2 |
|
ЧАСТИНА I (3 бали) Завдання 1-3 містять по 4 варіанти відповідей, з яких тільки ОДНА відповідь є ПРАВИЛЬНОЮ. Виберіть правильну, на вашу думку, відповідь і запишіть її в зошит. |
|
|
1. Обчисліть: |
|
|
1) |
|
|
а) –128; б) –2; в) 2; г) Інша |
а) 513; б) –3; в) 9; г) Інша |
|
2) |
2) |
|
а) 9; б) 13; в) 3; г) –1. |
а) –8; б) –10; в) 14; г) 152. |
|
3) |
3) |
|
а) 81; б) 20,25; в) 3; г) 9.
|
а) 81; б) 9; в) 3; г) 20,25. |
|
ЧАСТИНА II (6 балів) 2. Спростіть вираз |
|
|
|
|
|
3. Розв’яжіть рівняння: |
|
|
|
|
|
4. Знайти область визначення функції |
|
|
|
|
|
ЧАСТИНА III (3 бали ) 5. Розв’яжіть систему рівнянь |
|
|
|
|
Тема 4. Ірраціональні рівняння та нерівності
Самостійна робота 1
Розв’язування ірраціональних рівнянь
|
Варіант 1 |
Варіант 2 |
|
1. Розв’язати рівняння: |
|
|
1)
2)
3)
4) |
1)
2)
3)
4) |
|
2. Розв’язати систему рівнянь: |
|
|
|
|
Самостійна робота 2
Розв’язування ірраціональних нерівностей
|
Варіант 1 |
Варіант 2 |
|
1. Розв’язати нерівність: |
|
|
1)
2)
3)
4) |
1)
2)
3)
4) 4) |
Контрольна робота № 4
«Ірраціональні рівняння та нерівності»
|
Варіант 1 |
Варіант 2 |
|
1. Розв’яжіть рівняння : |
|
|
1)
2) |
1)
2) |
|
2. Розв’яжіть нерівність: |
|
|
|
|
|
3. Розв’яжіть рівняння : |
|
|
1)
2)
3) |
1)
2)
3) |
|
4. Розв’яжіть нерівність: |
|
|
1)
2) |
1)
2) |
|
5. Розв’яжіть систему рівнянь: |
|
|
|
|
III. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Тема 5. Властивості та графіки тригонометричних функцій
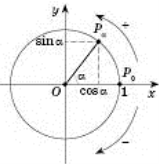 Означення. Синусом кута
Означення. Синусом кута ![]() (в радіанах) називається ордината точки
(в радіанах) називається ордината точки ![]() одиничного кола, яку отримують внаслідок повороту точки
одиничного кола, яку отримують внаслідок повороту точки ![]() на кут
на кут ![]() навколо точки
навколо точки ![]() .
.
Означення. Косинусом кута ![]() (в радіанах) називається абсциса точки
(в радіанах) називається абсциса точки ![]() одиничного кола, яку отримують внаслідок повороту точки
одиничного кола, яку отримують внаслідок повороту точки ![]() на кут
на кут ![]() навколо точки
навколо точки ![]() .
.
Означення. Тангенсом кута ![]() називається відношення
називається відношення ![]()
Означення. Котангенсом кута ![]() називається відношення
називається відношення ![]()
♦ Значення тригонометричних функцій деяких кутів
|
|
в град. |
|
|
|
|
|
|
|
|
|
в рад. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
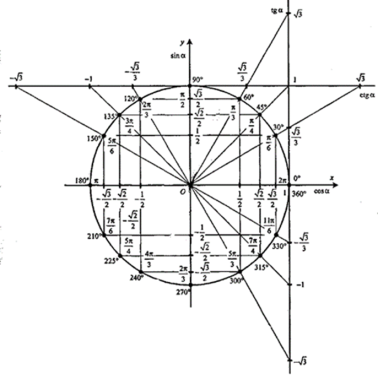
♦ Знаки тригонометричних функцій
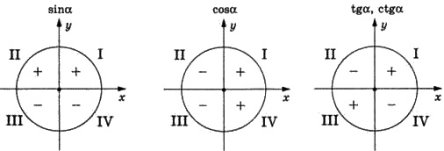
♦ Деякі властивості тригонометричних функцій
Парність і непарність
![]() – парна,
– парна,
![]()
![]()
![]() – непарні.
– непарні.
Періодичність
![]() – період
– період ![]() тоді
тоді
![]()
![]()
![]() – період
– період ![]() , тоді
, тоді ![]()
![]()
![]()
Якщо ![]() – період функції, то
– період функції, то ![]() – також періоди цієї функції
– також періоди цієї функції ![]() – загальний період для всіх функцій
– загальний період для всіх функцій ![]()
![]() .
.
♦ Графіки тригонометричних функцій
-
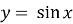 .
.
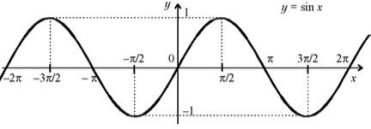
-
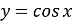 .
.

-
 .
.
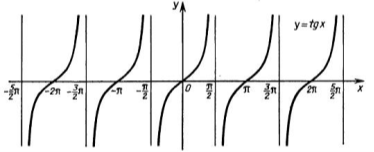
-
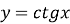 .
.
Самостійна робота 1
Властивості тригонометричних функцій. Період функцій
|
Варіант 1 |
Варіант 2 |
|
1. Знайти значення виразу : |
|
|
1)
2)
3) |
1)
2)
3) |
|
2. Визначити знак виразу : |
|
|
1)
2)
3) |
1)
2)
3) |
|
3. Обчисліть значення тригонометричних функцій: |
|
|
|
|
|
4. Знайдіть період функції: |
|
|
|
|
|
5. Спростіть вираз: |
|
|
1)
2) |
Самостійна робота 2
Властивості тригонометричних функцій.
Побудова графіків тригонометричних функцій
|
Варіант 1 |
Варіант 2 |
|
Побудувати графік функції: |
|
|
|
Контрольна робота № 5
«Властивості та графіки тригонометричних функцій»
|
Варіант 1 |
Варіант 2 |
|
|
|
|
1)
2) |
|
|
|
|
|
|
|
|
1)
2) |
1)
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема 6. Співвідношення між тригонометричними функціями одного аргументу
|
|
|
|
|
|
|
|
|
♦ Формули додавання
-
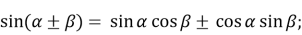
-
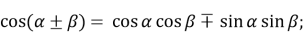
-
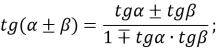
-
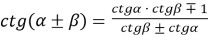 .
.
♦ Формули подвійного аргументу
1) ![]()
2) ![]()
3) ![]()
4) ![]()
♦ Формули перетворення суми в добуток
1) ![]()
2) ![]()
3) ![]()
4)![]()
♦ Формули перетворення добутку в суму
♦ Формули потрійного аргументу
♦ Формули половинного аргументу
-
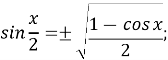
-
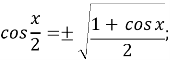
-
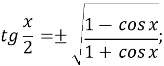
-
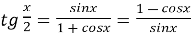 ,
, 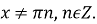
♦ Формули пониження степеня
♦ Правила зведення
Правило:
-
якщо зміна кута відбувається навколо вертикального діаметра
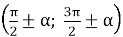 , то назва даної функції змінюється на кофункцію (синус на косинус, тангенс на котангенс і навпаки);
, то назва даної функції змінюється на кофункцію (синус на косинус, тангенс на котангенс і навпаки);
-
якщо зміна кута відбувається навколо горизонтального діаметра
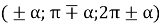 , то назва даної функції не змінюється;
, то назва даної функції не змінюється;
- перед утвореною функцією ставиться той знак, який має функція, що перетворюється.
Самостійна робота 1
Тригонометричні формули додавання. Формули зведення
|
Варіант 1 |
Варіант 2 |
|
|
||
|
1)
2)
3) |
1)
2)
3) |
|
|
||
|
|
|
|
|
||
|
1)
2) |
1)
2) |
|
|
||
|
|
|
|
|
5. Дано:
Знайти : |
5. Дано :
Знайти : |
|
Самостійна робота 2
Тригонометричні формули
|
Варіант 1 |
Варіант 2 |
|||||||||||||||||||
|
Обчисліть: |
||||||||||||||||||||
|
1) |
1) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2) |
2) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
3) |
3) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
4. Установіть відповідність між виразами (1-4) і виразами, отриманими в результаті їх спрощення (А-Д) |
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
5. Перетворіть суму на добуток: |
5. Перетворіть кожну суму на добуток і спростіть: |
|||||||||||||||||||
|
6. Перетворіть добуток на суму: |
||||||||||||||||||||
|
|
|
|||||||||||||||||||
|
7. Спростіть: |
||||||||||||||||||||
|
|
|
|||||||||||||||||||
Самостійна робота 3
Перетворення тригонометричних виразів
|
Варіант 1 |
Варіант 2 |
||
|
|||
|
1)
2)
3)
4) |
1)
2)
3)
4) |
||
|
|||
|
|
|
|
|
|
|||
|
|
|
||
|
|||
|
|
|
||
|
|||
|
|
|
||
Контрольна робота № 6
«Співвідношення між тригонометричними функціями
одного аргументу»
|
Варіант 1 |
Варіант 2 |
|
|
|
1) |
1) |
|
|
|
|
|
|
|
|
1)
2) |
1)
2) |
|
|
|
3) |
1)
2)
3) |
|
|
|
|
|
|
|
|
1)
2)
3) |
1)
2)
3) |
|
|
|
|
|
IV. ТРИГОНОМЕТРИЧНІ РІВНЯННЯ І НЕРІВНОСТІ
Тема 7. Обернені тригонометричні функції. Основні способи розв’язування тригонометричних рівнянь
♦ Означення.
Арксинусом числа b, де ![]() називають таке число
називають таке число ![]() з проміжку
з проміжку ![]() синус якого дорівнює b. Позначається:
синус якого дорівнює b. Позначається: ![]()
Арккосинусом числа b, де ![]() називають таке число
називають таке число ![]() з проміжку
з проміжку ![]() косинус якого дорівнює b. Позначається:
косинус якого дорівнює b. Позначається: ![]()
Арктангенсом числа b, де ![]() називають таке число
називають таке число ![]() з проміжку
з проміжку ![]() тангенс якого дорівнює b. Позначається:
тангенс якого дорівнює b. Позначається: ![]()
Арккотангенсом числа b, де ![]() називають таке число
називають таке число ![]() з проміжку
з проміжку ![]() котангенс якого дорівнює b. Позначається:
котангенс якого дорівнює b. Позначається: ![]()
♦ Властивості
♦ Найпростіші тригонометричні рівняння
частинні випадки:
![]()
![]()
![]()
частинні випадки:
![]()
![]()
![]()
♦ Деякі типи тригонометричних рівнянь
Рівняння виду ![]() або
або ![]() де
де ![]() – деякі числа, є однорідними.
– деякі числа, є однорідними.
-
Рівняння
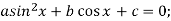
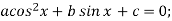 зводяться до квадратних відносно нової змінної t, де
зводяться до квадратних відносно нової змінної t, де 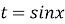 або
або 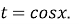
-
Рівняння
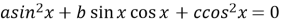 зводиться до рівняння
зводиться до рівняння 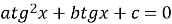 або
або 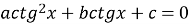 почленним діленням на
почленним діленням на 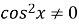 або
або 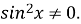
-
Рівняння виду
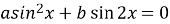 можна розв’язати за допомогою розкладання на множники (звести до одного аргументу, застосувавши формулу подвійного кута).
можна розв’язати за допомогою розкладання на множники (звести до одного аргументу, застосувавши формулу подвійного кута).
-
Рівняння
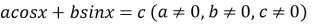 можна подати у вигляді
можна подати у вигляді 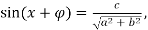 де
де 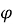 – допоміжний кут, такий що
– допоміжний кут, такий що 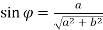 ,
, 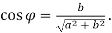
- Використання рівності однойменних тригонометричних функцій при розв’язуванні тригонометричних рівнянь:
якщо ![]() то
то ![]()
якщо ![]()
- Універсальна підстановка для розв’язуванні тригонометричних рівнянь:
![]()
![]()
- Формули пониження степеня:
![]() ;
; ![]()
Найпростіші тригонометричні нерівності – це нерівності виду ![]()
![]()
![]()
![]() (аналогічні нерівності для функцій
(аналогічні нерівності для функцій ![]()
![]() та
та ![]() ).
).
Вісь синусів співпадає з віссю Оу, вісь косинусів – з віссю Ох, вісь тангенсів – це пряма х = 1, вісь котангенсів – це пряма у = 1.
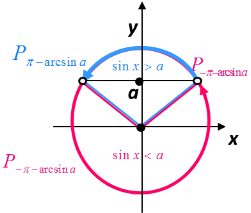 ♦ Схема розв’язування нерівності
♦ Схема розв’язування нерівності![]()
![]()
![]()
![]() .
.
-
на осі
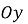 позначити число
позначити число 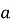 .
.
-
провести пряму
 (через число а паралельно осі Ох).
(через число а паралельно осі Ох).
-
позначити точки перетину прямої у = а з одиничним колом у вигляді порожнього кружечка, якщо нерівність строга, або зафарбованого, якщо вона нестрога, та вкажіть відповідні точки
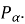
-
якщо нерівність містить
знак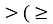 ), то вибрати дугу кола, розташовану вище прямої
), то вибрати дугу кола, розташовану вище прямої  , а якщо знак
, а якщо знак 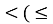 ) – нижче прямої
) – нижче прямої  .
.
- за допомогою стрілки вказати на дузі додатний напрям.
- записати відповідь у вигляді проміжку від початку дуги до кінця (стрілки), враховуючи періодичність функції.
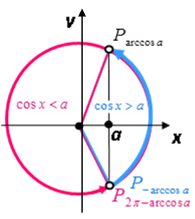 ♦ Схема розв’язування нерівності
♦ Схема розв’язування нерівності ![]()
![]()
![]()
- на осі Ох позначити число а.
-
провести пряму
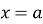 (через число а паралельно осі Оу).
(через число а паралельно осі Оу).
-
позначити точки перетину прямої
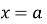 з одиничним колом у вигляді порожнього кружечка, якщо нерівність строга, або зафарбованого, якщо вона нестрога, та вкажіть відповідні точки
з одиничним колом у вигляді порожнього кружечка, якщо нерівність строга, або зафарбованого, якщо вона нестрога, та вкажіть відповідні точки 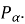
-
якщо нерівність містить знак
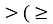 ), то вибрати дугу кола, розташовану праворуч від прямої х = а, а якщо знак
), то вибрати дугу кола, розташовану праворуч від прямої х = а, а якщо знак ) – ліворуч від прямої.
) – ліворуч від прямої.
- за допомогою стрілки вказати на дузі додатний напрям.
- записати відповідь у вигляді проміжку від початку дуги до кінця (стрілки), враховуючи періодичність функції.
♦ Схема розв’язування нерівності ![]()
![]()
-
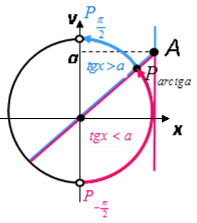 провести вісь тангенсів (пряма паралельна осі Оу і є дотичною до одиничного кола у точці
провести вісь тангенсів (пряма паралельна осі Оу і є дотичною до одиничного кола у точці 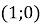 ).
).
-
на осі тангенсів позначити точку
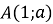 .
.
-
cполучити точку А з початком координат і позначити точку перетину відрізка ОА з одиничним колом
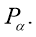
-
якщо нерівність містить знак
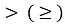 , то вибрати дугу кола від точки
, то вибрати дугу кола від точки 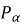 до точки
до точки 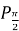 , а якщо знак
, а якщо знак 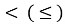 – вибрати дугу кола від точки
– вибрати дугу кола від точки 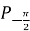 до точки
до точки 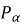 .
.
- записати відповідь у вигляді проміжку від початку дуги до кінця (стрілки), враховуючи періодичність функції.
Функція ![]() визначена при
визначена при ![]() .
.
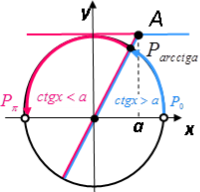 ♦ Схема розв’язування нерівності
♦ Схема розв’язування нерівності ![]()
![]()
-
провести вісь котангенсів (пряма паралельна осі Ох і є дотичною до одиничного кола у точці
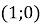 ).
).
-
на осі котангенсів позначити точку
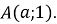
-
сполучити точку
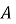 з початком координат і позначити точку перетину відрізка ОА з одиничним колом
з початком координат і позначити точку перетину відрізка ОА з одиничним колом 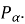
-
якщо нерівність містить знак
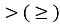 , то вибрати дугу кола від точки
, то вибрати дугу кола від точки 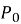 до точки
до точки 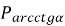 , а якщо знак
, а якщо знак 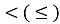 – вибрати дугу кола від точки
– вибрати дугу кола від точки 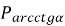 до точки
до точки 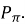
- Записати відповідь у вигляді проміжку від початку дуги до кінця (стрілки), враховуючи періодичність функції.
Функція ![]() визначена при
визначена при ![]()
Самостійна робота 1
Найпростіші тригонометричні рівняння.
Тригонометричні рівняння виду ![]()
|
Варіант 1 |
Варіант 2 |
|
Розв’язати рівняння: |
|
|
3)
4)
5)
6)
7)
8)
9) |
2)
3)
4)
5)
6)
7)
8)
9) |
Самостійна робота 2
Основні способи розв’язування тригонометричних рівнянь
|
Варіант1 |
Варіант 2 |
|
Розв’яжіть рівняння: |
|
|
|
|
Контрольна робота № 7
«Обернені тригонометричні функції. Основні способи розв’язування тригонометричних рівнянь»
|
Варіант 1 |
Варіант 2 |
||
|
|||
|
|
|
||
|
|||
|
|
|
|
|
|
3. Розв’язати рівняння: |
|||
|
|
|
||
|
4. Знайдіть корені рівняння: |
|||
|
|
|
||
|
5. Знайдіть найбільший від’ємний корінь рівняння: |
5. Знайдіть найменший додатний корінь рівняння |
||
Тема 8. Тригонометричні нерівності
Самостійна робота 1
Розв’язування систем тригонометричних рівнянь
|
Варіант1 |
Варіант 2 |
|
Розв’яжіть системи рівнянь: |
|
|
|
|
Самостійна робота 2
Розв’язування тригонометричних нерівностей
|
Варіант 1 |
Варіант 2 |
|
Розв’язати нерівність: |
|
|
|
Самостійна робота 3
Розв’язування тригонометричних рівнянь та нерівностей
з параметрами
|
Варіант 1 |
Варіант 2 |
|
1. Розв’язати нерівність: |
|
|
1)
2)
3) |
1)
2)
3) |
|
2. Розв’язати рівняння: |
|
|
|
|
|
3. Розв’язати рівняння для всіх значень параметра a: |
|
|
1)
2) |
1)
2) |
Контрольна робота № 8
«Тригонометричні нерівності»
|
Варіант 1 |
Варіант 2 |
|
|
|
|
|
|
2. Розв’язати нерівність: |
|
|
1)
2)
3)
4) |
|
|
|
|
|
V. ГРАНИЦЯ ТА НЕПЕРЕРВНІСТЬ ФУНКЦІЇ. ПОХІДНА ТА її ЗАСТОСУВАННЯ
Тема 9. Похідна функції
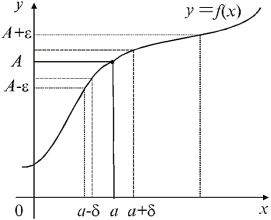 Означення. Число А називається границею функції
Означення. Число А називається границею функції ![]() при
при ![]() , що прямує до a
, що прямує до a ![]() , якщо для будь-якого
, якщо для будь-якого ![]() існує число
існує число ![]() таке, що із нерівності
таке, що із нерівності ![]() випливає нерівність
випливає нерівність ![]() Записують так:
Записують так: ![]()
♦ Теореми про границю
-
Якщо функція
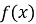 має границю при
має границю при 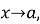 то ця границя – єдина.
то ця границя – єдина.
-
Границя неперервної функції при
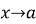 дорівнює значенню функції в точці a.
дорівнює значенню функції в точці a.
- Границя сталої функції дорівнює цій же сталій
![]() де
де ![]() – стала.
– стала.
- Границя суми (різниці) двох функцій дорівнює сумі (різниці) їхніх границь, при умові, що границі доданків існують
![]()
- Границя добутку двох функцій дорівнює добутку границь цих функцій, якщо границі множників існують
![]()
- Сталий множник можна виносити за знак границі
![]()
-
Границя частки двох функцій дорівнює частці границь цих функцій, якщо границі чисельника і знаменника існують і границя знаменника не дорівнює нулю
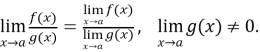
♦ Перша визначна границя ![]()
Нехай функція![]() визначена на всій числовій прямій. Число В називається границею
визначена на всій числовій прямій. Число В називається границею ![]() при
при ![]() , якщо для довільного
, якщо для довільного ![]() знайдеться таке число
знайдеться таке число ![]() що для всіх
що для всіх ![]() які задовольняють
які задовольняють ![]() виконується нерівність
виконується нерівність ![]()
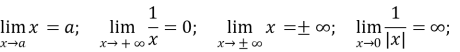
Якщо ![]() то
то ![]()
Якщо ![]() то
то ![]()
Якщо ![]() і
і ![]() то
то ![]()
♦ Способи обчислення границь
-
Для будь-якого многочлена
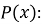
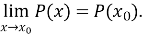
-
Якщо число
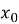 входить до області визначення дробово-раціональної функції
входить до області визначення дробово-раціональної функції 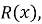 то
то 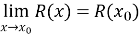 .
.
-
Якщо в результаті підстановки
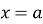 одержали вираз
одержали вираз 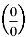 , то:
, то:
а) спробувати розкласти чисельник та знаменник на множники і скоротити дріб;
б) якщо дріб не можна скоротити, то слід чисельник і знаменник домножити на вираз, спряжений із знаменником (або чисельником), а потім скоротити дріб;
в) якщо під знаком границі стоять тригонометричні функції або обернені тригонометричні функції, то зводимо до першої визначеної границі ![]()
![]()
![]()
![]()
![]() якщо
якщо ![]()
![]()
Означення. Похідною функції ![]() у даній точці x називається границя відношення приросту функції
у даній точці x називається границя відношення приросту функції ![]() до відповідного приросту аргументу
до відповідного приросту аргументу ![]() за умови, що
за умови, що ![]() тобто
тобто
![]() (за умови, що ця границя існує). Функція, яка має похідну, називається диференційованою.
(за умови, що ця границя існує). Функція, яка має похідну, називається диференційованою.
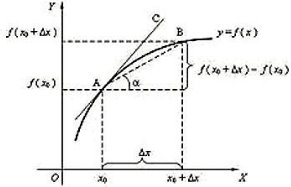 ♦ Геометричний зміст похідної. Дотичною до кривої в даній точці А називається граничне положення січної АВ, коли точка В прямує вздовж кривої до точки А. Значення похідної в точці
♦ Геометричний зміст похідної. Дотичною до кривої в даній точці А називається граничне положення січної АВ, коли точка В прямує вздовж кривої до точки А. Значення похідної в точці ![]() дорівнює тангенсу кута нахилу дотичної до графіка функції в точці з абсцисою
дорівнює тангенсу кута нахилу дотичної до графіка функції в точці з абсцисою ![]() і дорівнює кутовому коефіцієнту цієї дотичної.
і дорівнює кутовому коефіцієнту цієї дотичної.
![]() – кутовий коефіцієнт дотичної з рівнянням
– кутовий коефіцієнт дотичної з рівнянням ![]() .
.
![]()
![]() – рівняння дотичної до графіка функції
– рівняння дотичної до графіка функції ![]() в точці з абсцисою
в точці з абсцисою ![]() .
.
♦ Механічний зміст похідної. Похідна характеризує швидкість зміни функції при зміні аргументу; похідна за часом є міра швидкості зміни, застосована до найрізноманітніших фізичних величин. Якщо функція ![]() описує рух матеріальної точки, тобто залежність пройденої відстані
описує рух матеріальної точки, тобто залежність пройденої відстані ![]() від часу
від часу ![]() , то її похідна задає залежність миттєвої швидкості
, то її похідна задає залежність миттєвої швидкості ![]() від часу
від часу ![]() ,
, ![]() ; похідна швидкості відповідно є прискоренням
; похідна швидкості відповідно є прискоренням ![]()
♦ Таблиця похідних функцій
|
Функція |
Похідна |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
♦ Таблиця похідних складених функцій
|
Функція |
Похідна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
♦ Правила диференціювання
- Сталий множник можна виносити за знак похідної.
![]() – константа.
– константа.
-
Похідна суми функцій:
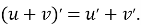
- Похідна добутку функцій:
![]()
-
Похідна частки функцій:
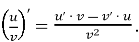
- Похідна складеної функції (функції від функції):
![]()
Самостійна робота 1
Похідна функції. Похідна складеної функції. Рівняння дотичної
|
Варіант 1 |
Варіант 2 |
|
|
|
1)
2)
3)
4) |
1)
2)
3)
4) |
|
|
|
|
|
|
|
|
|
|
|
4. Знайти рівняння дотичної до графіка функції |
4. Знайти рівняння дотичної до графіка функції
|
Контрольна робота № 9
«Похідна функції»
|
Варіант 1 |
Варіант 2 |
|
|
|
1)
2)
3)
4)
5)
6) |
1)
2)
3)
4)
5)
6)
|
|
|
|
|
|
|
|
|
Знайти швидкість руху в момент часу |
Знайти швидкість руху в момент часу |
|
4. Скласти і розв’язати рівняння
|
4. Розв’язати нерівність |
|
5. Знайти множину розв’язків нерівності
|
5. Скласти і розв’язати рівняння
|
Тема 10. Дослідження функцій за допомогою похідної
♦ Застосування похідної.
-
Рівняння дотичної, яка проходить через точку
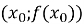 знаходимо:
знаходимо:
-
записуємо рівняння дотичної
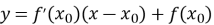 ;
;
-
знаходимо
 ;
;
-
знаходимо
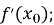
-
значення
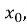
 і
і 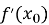 підставляємо у рівняння.
підставляємо у рівняння.
♦ Проміжки монотонності та екстремуми функції.
Достатні умови:
-
Якщо функція
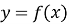 диференційована і зростає на деякому проміжку, то її похідна на цьому проміжку не від’ємна. Тобто, якщо
диференційована і зростає на деякому проміжку, то її похідна на цьому проміжку не від’ємна. Тобто, якщо 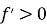 на проміжку, то функція зростає на цьому проміжку.
на проміжку, то функція зростає на цьому проміжку.
-
Якщо функція
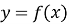 диференційована і спадає на деякому проміжку, то її похідна на цьому проміжку не додатна. Тобто, якщо
диференційована і спадає на деякому проміжку, то її похідна на цьому проміжку не додатна. Тобто, якщо 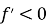 на проміжку, то функція спадає на цьому проміжку.
на проміжку, то функція спадає на цьому проміжку.
-
Внутрішні точки області визначення функції
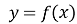 , у яких похідна дорівнює нулю, називають стаціонарними. Отже, для того щоб точка
, у яких похідна дорівнює нулю, називають стаціонарними. Отже, для того щоб точка 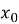 була точкою екстремуму, необхідно, щоб вона була стаціонарною.
була точкою екстремуму, необхідно, щоб вона була стаціонарною.
- Якщо похідна ліворуч стаціонарної точки від’ємна, а праворуч – додатна, тобто при переході через стаціонарну точку похідна змінює знак з «–» на «+», то ця стаціонарна точка є точкою мінімуму.
- Якщо похідна ліворуч стаціонарної точки додатна, а праворуч – від’ємна, тобто при переході через стаціонарну точку похідна змінює знак з «+» на «–», то ця стаціонарна точка є точкою максимуму.
- Якщо при переході через стаціонарну точку похідна не змінює знак, тобто ліворуч і праворуч від стаціонарної точки похідна додатна або від’ємна, то ця точка не є точкою екстремуму.
♦ Проміжки опуклості й точки перегину.
Функція ![]() , визначена на проміжку
, визначена на проміжку ![]() , називається опуклою донизу (догори), якщо на цьому проміжку її графік розміщено не нижче (не вище) дотичної до графіка, проведеної в довільній його точці.
, називається опуклою донизу (догори), якщо на цьому проміжку її графік розміщено не нижче (не вище) дотичної до графіка, проведеної в довільній його точці.
Якщо функція неперервна у точці ![]() і змінює характер опуклості при переході через цю точку, тоді точка
і змінює характер опуклості при переході через цю точку, тоді точка ![]() називається точкою перегину.
називається точкою перегину.
Достатня умова для визначення характеру опуклості функції:
Якщо при ![]() функція є диференційованою і виконується нерівність
функція є диференційованою і виконується нерівність ![]() , то функція опукла донизу на цьому проміжку.
, то функція опукла донизу на цьому проміжку.
Якщо при ![]() виконується нерівність
виконується нерівність ![]() , то функція опукла догори на цьому проміжку.
, то функція опукла догори на цьому проміжку.
Якщо ![]() , причому ліворуч і праворуч від точки
, причому ліворуч і праворуч від точки ![]()
![]() має різні знаки, то
має різні знаки, то ![]() – точка перегину.
– точка перегину.
♦ Найбільше та найменше значення функції.
Теорема Вейєрштрасса. Якщо функція ![]() неперервна на відрізку
неперервна на відрізку ![]() то серед її значень на цьому відрізку є найменше і найбільше.
то серед її значень на цьому відрізку є найменше і найбільше.
Алгоритм знаходження найменшого та найбільшого значення функції ![]() , яка має на відрізку
, яка має на відрізку ![]() скінченну кількість критичних точок:
скінченну кількість критичних точок:
-
знайти критичні точки функції
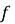 на інтервалі
на інтервалі 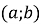 ;
;
-
обчислити значення функції
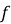 у критичних точках;
у критичних точках;
-
обчислити
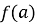 і
і 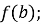
- серед знайдених значень функції вибрати найбільше і найменше.
Це і будуть найбільше: ![]() та найменше:
та найменше: ![]() значення функції
значення функції ![]() на відрізку
на відрізку ![]() .
.
♦ Досліждження функції та побудова її графіка.
Алгоритм досліждження функції та побудова її графіка:
-
Знаходимо область визначення функції
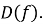
- Знаходимо точки перетину графіка з координатними осями.
- З’ясовуємо парність (непарність), періодичність функції.
- Знаходимо похідну та стаціонарні точки.
- Знаходимо проміжки зростання, спадання, точки екстремуму та екстремальні значення функції.
- З’ясовуємо поведінку функції на кінцях області визначення.
- На підставі проведеного дослідження будуємо графік функції.
Самостійна робота 1
Проміжки монотонності функції. Екстремуми функції
|
Варіант 1 |
Варіант 2 |
|
|
1. Знайдіть стаціонарні точки функції : |
||
|
|
|
|
|
2. Знайдіть екстремуми функції |
||
|
|
|
|
|
3. Знайдіть проміжки монотонності функції: |
||
|
|
|
|
|
4. Знайдіть точки екстремуму функції : |
||
|
|
|
|
Самостійна робота 2
Дослідження функції за допомогою похідної.
Побудова графіка функції
|
Варіант 1 |
Варіант 2 |
|
Дослідіть функцію та побудуйте її графік: |
|
|
|
Самостійна робота 3
Найбільше та найменше значення функції
|
Варіант 1 |
Варіант 2 |
|
1. Знайдіть найменше та найбільше значення функції на заданому відрізку : |
|
|
|
|
|
2. З усіх прямокутників з діагоналлю 18 см знайдіть прямокутник з найбільшої площі. |
2. З усіх прямокутників з площею 25 |
|
3. Знайдіть найменше та найбільше значення функції
|
3. Знайдіть найменше та найбільше значення функції
|
Контрольна робота № 10
«Дослідження функцій за допомогою похідної»
|
Варіант 1 |
Варіант 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. З усіх прямокутників з діагоналлю 18 см знайдіть прямокутник найбільшої площі. |
5. Число 12 представити у вигляді суми двох додатних доданків так, щоб сума їх квадратів була найменшою. |
|
6. При яких значеннях параметра а точка
|
6. При яких значеннях параметра а точка
|
Тема 11. Застосування похідної до розв’язування задач, зокрема прикладного змісту
Самостійна робота 1
Проміжки опуклості та увігнутості функції
|
Варіант 1 |
Варіант 2 |
|
|
|
|
|
|
|
|
|
|
Самостійна робота 2
Застосування похідної до розв’язування рівнянь та нерівностей
|
Варіант 1 |
Варіант 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольна робота № 11
«Застосування похідної до розв’язування задач,
зокрема прикладного змісту»
|
Варіант 1 |
Варіант 2 |
|
|
|
|
|
|
|
|
|
|
|
3. Знайдіть тангенс кута нахилу дотичної проведеної до графіка функції |
3. Знайдіть тангенс кута нахилу дотичної проведеної до графіка функції |
|
4. Число 14 представити у вигляді суми трьох додатних доданків так, що перший відноситься до другого як 1:3, а сума куба першого та квадратів другого і третього набуває найменшого значення. |
4. Число 24 представити у вигляді суми трьох додатних доданків так, що перший відноситься до другого як 1:2, а сума кубів першого і другого та квадрата третього набуває найменшого значення. |
|
5. Обчисліть площу трикутника, утвореного осями координат і дотичною до графіка функції
|
5. Складіть рівняння дотичної до графіка функції |
VI. ПОВТОРЕННЯ, УЗАГАЛЬНЕННЯ ТА СИСТЕМАТИЗАЦІЯ НАВЧАЛЬНОГО МАТЕРІАЛУ, РОЗВ’ЯЗУВАННЯ ЗАДАЧ
Самостійна робота 1
Функції, їхні властивості та графіки.
Розв’язування рівнянь та нерівностей
(повторення)
|
Варіант 1 |
Варіант 2 |
|
|
|
|
1)
3) |
|
|
|
|
|
|
|
|
|
|
Самостійна робота 2
Степеневі функції, їхні властивості та графіки
(повторення)
|
Варіант 1 |
Варіант 2 |
|
|
|
1)
2)
3) |
|
|
|
1)
2) |
1)
2) |
|
|
|
1)
2)
3) |
1)
2)
3) |
Самостійна робота 3
Тригонометричні функції.
Тригонометричні рівняння та нерівності (повторення)
|
Варіант 1 |
Варіант 2 |
|
1. Розв’яжіть нерівності : |
|
|
|
|
2. Розв’язати рівняння : |
|
|
1)
2) |
|
|
3. При яких значеннях параметра a рівняння |
|
|
|
|
Підсумкова контрольна робота за рік
|
Варіант 1 |
Варіант 2 |
|
1. Спростити вираз: |
|
|
2)
3) |
|
2. Розв’яжіть нерівність: |
|
|
|
|
|
3. Складіть рівняння дотичної до графіка функції |
3. Знайдіть рівняння горизонтальних дотичних до графіка функції
|
|
4. Дослідити функцію та побудувати її графік. |
|
|
|
|
|
5. Знайти, при яких значеннях параметра а має розв’язки рівняння: |
|
|
|
|
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
- Сімонова Н.Д. Помічник з алгебри та початків аналізу. Довідник з алгоритмами розв’язання задач. – Харків.: Видавнича група «Основа», 2004. – 186 с.
- Гальперіна А.Р., Золотарьова І.О. Алгебра і початки аналізу. 10 клас: Збірник завдань для контролю знань. – ТОВ «Видавництво «Ранок», 2010. – 176 с.
- Мерзляк А. Г., Полонський В. Б., та ін. Алгебра. 11 клас: Збірник задач і контрольних робіт. – Харків.: Гімназія, 2016. – 95 с.
- Мерзляк А. Г., Полонський В. Б., та ін. Алгебра і початки аналізу. 10 клас. Профільний рівень.: Збірник задач і контрольних робіт. – Харків.: Гімназія, 2018. – 143 с.
- Єршова А.П., Голобородько В.В. Алгебра і початки аналізу. 10 – 11 клас.: Самостійні та контрольні роботи. – Харків.: Гімназія, 2004. – 176 с.
- Роганін О.М. Шкільний курс математики.: Короткий довідник. – Харків.: «Факт», 2005. – 144 с.
- Алгебра і початки аналізу в таблицях. 7 – 11 класи. Навчальний посібник. Науково-методичний центртм, 2003. – 248 с.
- Пастушенко С.М., Підченко Ю.П. Вища математика. Основні поняття, формули, зразки розв’язування задач.: Посібник для студентів вищих закладів освіти. – Київ, 2003. – 160 с.
- https://www.slideshare.net/Lou24112013/ss-41298284
- https://subject.com.ua/mathematics/zno/99.html
- https://znanija.com/task/23758981
- https://mathab.com.ua/pochatki-analizu/poxidna/poxidna-funkciї-її-geometrichnij-ta-mexanichnij-zmist.html
1


про публікацію авторської розробки
Додати розробку

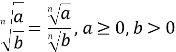
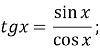
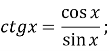


-

Яцейко Галина
12.01.2025 в 20:13
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Крупник Людмила Віталіївна
15.01.2024 в 21:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Lysyuk P
16.12.2023 в 15:22
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Конончук Назар Анатолійович
30.09.2022 в 08:14
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Качурина Виктория
26.10.2021 в 01:00
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука