Урок "Застосування інтеграла до обчислення площ плоских фігур"

Тема заняття. Застосування інтеграла до обчислення площ плоских фігур

Мета заняття:

Навчальна: узагальнити і систематизувати знання студентів з теми «Інтеграл та його застосування»; сприяти закріпленню знань про геометричний, фізичний та економічний зміст інтеграла; формувати вміння й навички студентів самостійно систематизувати та поглиблювати знання, використовувати їх у практичній діяльності, усунути ті прогалини в навчальних досягненнях студентів, які існують у засвоєнні теми

Розвиваюча: розвивати творчі здібності, культуру математичної мови, вміння проводити самоаналіз діяльності, бути опонентом, висловлювати свої думки, виражати почуття та використовувати свій досвід, брати на себе відповідальність за навчання та розвивати вміння вчитися, сприяти підвищенню інтересу до математики.

Виховна: виховувати комунікативні та інформаційні риси у студентів, активність та спостережливість, колективізм та вміння самостійно міркувати, узагальнювати та робити висновки, почуття успіху, бажання подолати труднощі, задовольнити інтереси.

Завдання:

закріплення, розширення та поглиблення знань студентів, отриманих раніше на заняттях;

формування й розвиток їх навичок самостійної роботи;

реалізація диференційованого підходу в навчанні з урахуванням індивідуальних особливостей студента;

Дидактична мета: 

забезпечити педагогічні умови для поглиблення і закріплення знань студентів з теми «Інтеграл та його застосування», набутих під час аудиторних занять та у процесі вивчення навчальної інформації, що виноситься на самостійне опрацювання;

спонукати студентів до колективного творчого обговорення найбільш складних питань навчального курсу, активізація їх до самостійного вивчення наукової та методичної літератури, формування у них навичок самоосвіти;

оволодіння методами аналізу фактів, явищ і проблем, що розглядаються та формування умінь і навичок до здійснення різних видів майбутньої професійної діяльності.

інтеграція сучасних педагогічних та інформаційних технологій підготовки майбутнього фахівця як соціально-адаптованої особистості відповідно до сучасних вимог ринку праці.

Обладнання:

А. Наочні посібники: навчальна презентація, комп’ютерні презентації студентів, портрети, відеофільми про І. Ньютона і Г. Лейбніца, стенд з основними формулами інтегрування.

Б. Роздатковий матеріал: картки індивідуальних досягнень студентів,  картки з тестовими завданнями.

В. ТЗН: ПК, проектор, екран.

Г. Література:    Г.П.Бевз, В.Г.Бевз Математика: Підруч. для 11 класу загальноосвітніх навчальних закладів. Рівень стандарту.

Алгебра і початки аналізу: Підруч.для 10-11 кл. загальноосвіт. навч. закладів / М.І. Шкіль, З.І. Слєпкань, О.С.Дубинчук – К.: Зодіак-ЕКО, 2000.-608с.

                                  Сила і загальність методу диференціального й               

                                  інтегрального числення такі, що не

                                  ознайомившись з ними, не можна як слід зрозуміти

                                  все значення математики для природознавства і

                                  техніки і навіть оцінити всю красу і принадність

                                  самої математичної науки.

      А.М.Колмогоров

Хід заняття

І. Організаційна  частина.

            Мобілізувати студентів до навчання; активізувати їхню увагу; створити робочу атмосферу для проведення заняття (містить привітання викладача зі студентами, виявлення відсутніх, перевірку підготовленості до заняття).

ІІ. Актуалізація опорних знань.

1. Фронтальне опитування.

1. Що називається первісною функції?

Відповідь. Функція F(х) називається первісною для функції f(х) на проміжку І, якщо для кожного значення х із цього проміжку F′(х) = f(х).

2. Скільки первісних має кожна функція i чим вони відрізняються?

Відповідь. Будь-які дві первісні функції для однієї і тієї самої функції відрізняються одна від одної на сталий доданок.

3. Геометрична інтерпретація основної властивості первісних. Побудувати графіки первісної функції f(х)=соѕх:

 F₁ (х) = sin х , F₂(х)=ѕіn х+1, F₃(х)=ѕіn х-2 та перевірити правильність виконання диференціюванням.

Відповідь.

4. Яка фігура називається криволінійною трапецією?

Відповідь. Фігуру, обмежену графіком функції у =  f(х), відрізком осі Ох і прямими х = а х = в, називають криволінійною трапецією.

Побудувати різні види криволінійних трапецій:

a) y = lg 3x, y=1, x=5.

Відповідь.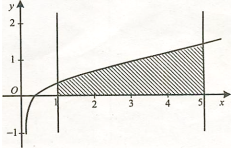

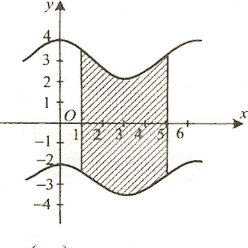
б)y = cos x+3, y = cos x-3, x=1, x=5.

Відповідь.

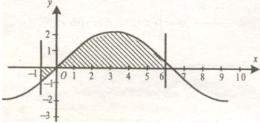
в) , x = -1, x = 6.

Відповідь.

5. Формула Ньютона – Лейбніца.

Відповідь.

2. Самостійна робота

Тестові завдання

Обчислити інтеграли функцій

1-й варіант

1.

А. 0   Б.  В.   Г. 1 Д. Інша відповідь

2.

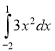
А. 9   Б.-7  В.-3  Г. -9 Д. Інша відповідь

3.

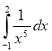
А. Б.  В.   Г.    Д. Інша відповідь

4.

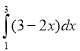
А.2  Б.-2  В.4  Г.3  Д. Інша відповідь

5.

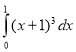
A.   Б.    В.   Г. 3   Д. Інша відповідь

6.

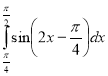
А.        Б.         В.         Г.        Д.  Інша відповідь

2-й варіант

1.

А. 2   Б.3  В.-3  Г. 4 Д. Інша відповідь

2.

А. 5   Б. 13  В. 10   Г. -5  Д. Інша відповідь

3.

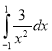
А. 6  Б.0    В.   Г. -6   Д. Інша відповідь

4.

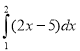
А.2  Б.-2  В.4  Г.3  Д. Інша відповідь

5.

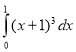
А.- 10   Б.    В.26   Г.10   Д. Інша відповідь

6.

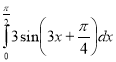
А.0        Б.         В.         Г.        Д.  Інша відповідь

ІІІ. Ознайомлення з методами обчислення площ плоских фігур.

 До поняття інтеграла привели потреби розв’язування задач з геометрії, фізики та багатьох інших. У шкільному курсі геометрії розглядаються формули для обчислення площ невеликої кількості фігур: многокутників, круга та його частин. Виникає запитання: як обчислити площу плоскої фігури, обмеженої довільною кривою? Виявляється, що розв'язати таку задачу можна за певних умов.

Усі плоскі фігури, площі яких можна обчислити  за допомогою інтеграла, поділяємо на 5 типів.

1. Площа криволінійної трапеції обчислюється за формулою

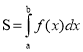, якщо

Демонструється фігура, обмежена графіками: у = е^x, у = 0, х = 1,х = 2.

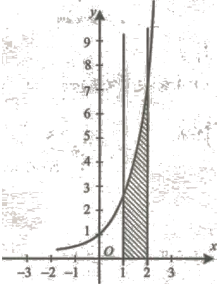
 2. Площа криволінійної трапеції обчислюється за формулою

, якщо

Демонструється фігура, обмежена графіками: у= -x⁴ - 4, у = 0, х = -2, х=2.

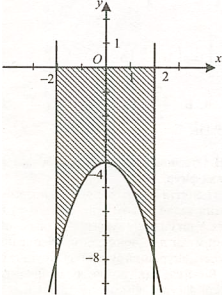
3. Площа фігури, обчислюється за формулою

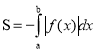
Демонструється фігура, обмежена графіками:

 у =  Зсоѕх, у = 0, х = - 8, х = 8.

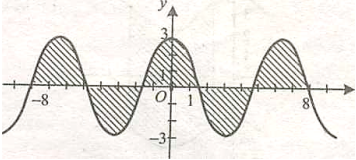
4. Площа фігури, обмеженої кривими та прямими х=а, х=b, обчислюється за формулою

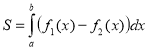
Демонструється фігура, обмежена графіками:

у= - (х-2)²+6, у = З+, х = 1, х = З.

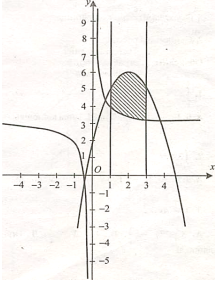
5. Площа фігури, обмеженої кривими у =f(х), y = g(х) , обчислюється за формулою

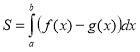
де а, b — корені рівняння f(х) —g(x) = 0.

Демонструється фігура, обмежена графіками:

f(x)=, g(x)=.

IV. Обчислення площ плоских фігур.

1.          Обчислити площу плоскої фігури, обмеженої графіком функції у = 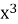, віссю Ох і прямою х = 2.

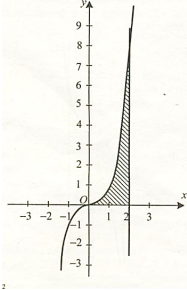
Розв’язання.

Зобразимо фігуру, площу якої треба знайти

у = , у = 0, х = 2.

S = dх = 4 (кв.од.)

2.          Фігура обмежена параболою 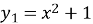, прямою 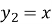+3

 Обчислити її площу.

      Розв’язання.

           Зобразимо фігуру, площу якої треба знайти

+3

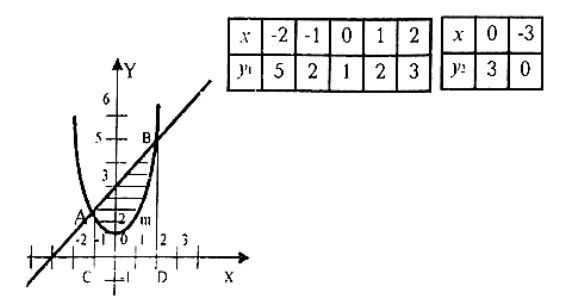
Знайдемо абсциси точок перетину даних  ліній – межі інтегрування.

Отже, а = -1, в = 2.

Обчислимо площу утвореної фігури S=.

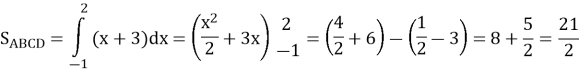
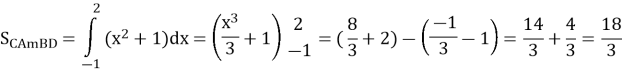
S=

Відповідь: 4,5 (кв.од).

3.          Фігура обмежена графіками функцій у = , . Обчислити її площу.

Розв’язання.

Зобразимо фігуру, площу якої треба знайти.

а)y= - графіком є гіпербола; у = 7 – х – пряма.

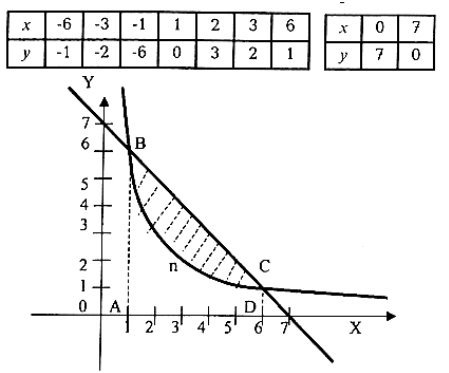
б) Знайдемо абсциси точок перетину даних  ліній – межі інтегрування.

за властивістю пропорції маємо:

6=7х-; – 7х + 6 = 0

За теоремою Вієта маємо:= 6; = 7.

= 6, = 1

або через дискримінант:

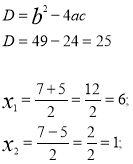
в) Шукана площа дорівнює різниці трапеції АВСD і криволінійної трапеції АВnCD.

=

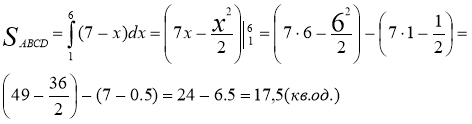
Відповідь:  

4.          Фігура обмежена графіками функцій  у = - ,

у = Обчислити її площу.

Розв’язання.

Зобразимо фігуру, площу якої треба знайти.

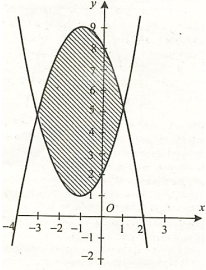
S= – 2х +8) – ())dх21,3 (кв.од.).

V. Розв'язування задач з професійним змістом.

1. Яка маса заготовки вказаної форми, виготовленої з листа сталі Ст. 3,

-10 мм;?  Фігура задана лініями

Розв'язання

Будуємо фігуру, обмежену графіками:

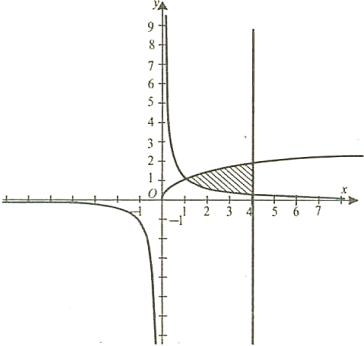
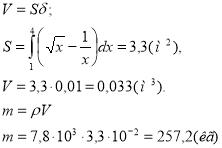
Відповідь: 257,2 кг

2. Розрахувати витрати цегли і розчину для зведення арки товщиною дві цеглини (цегла одинарна 250 х 120 х 65, товщина шва 10 мм) якщо на 1 м³ кладки витрачається 400 шт. цегли і 0,25 м³ розчинy. Зовнішню лінію арки задано функцією, а внутрішню

Розв’язання.

Будуємо фігуру, обмежену графіками:

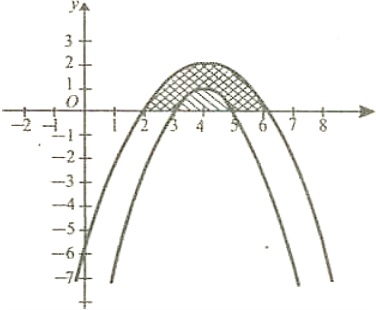
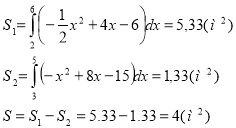
 Висота в 2 цеглини  h=250•2+ 10=510(мм) = 0,51 (м),

V=0,51•4=2,04=2,04 (м³).

Витрати цегли n= 2,04 • 400 = 816,

витрати розчину,m = 2,04 ° 0,25 = 0,51 (м³).

Відповідь. Витрати цегли 816 штук, розчину — 0,51 м³

3. Розрахувати витрати дерева для заготовки боковини стільця, якщо товщина дошки 2 см, а конфігурацію боковини задано лініями: у₁ = х³ + 4, у₂ = -2х² +2 , у₃ = 0, х = 1,6.

Розв'язання

Будуємо графіки функцій у₁ = х³ + 4, у₂ = -2х² +2 , у₃=0, х =1,6(масштаб:

1 поділка —1 дм).

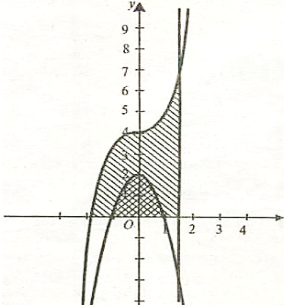
S=S₁-S₂

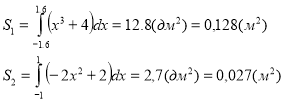
S = 0,128 – 0,027 = 0,101(м² )

V = Sh

V=0,1010,02 = 0,00202(м³)

Відповідь. Витрати деревини для виготовлення заготовки 0,00202 м³ .

VI. Підсумок заняття.

VIІ. Домашнє  завдання.

 За підручником вивчити Р.3 § 14, 15. Розв’язати вправи №№ 505, 507, 530.