Презентація до уроку "Розв'язування показникових нерівностей"
Про матеріал
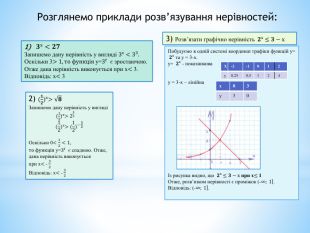
Ознайомлення з показниковими нерівностями. Розв'язування найпростіших показникових нерівностей та тих, що безпосередньо до них зводяться. Знайомство із способами розв'язку показникових нерівностей
Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку