Презентація до уроку "Властивості логарифмів"

Тема уроку: Властивості логарифмів

Мета: навчальна: вивчити основні властивості логарифмів та сформувати вміння й навички їх застосування до розв’язування вправ; розвиваюча: розвивати творче мислення, обчислювальні навички, вміння аналізувати, робити самостійні висновки; виховна: виховувати інтерес до математики, почуття відповідальності, культуру діалогу, впевненість при прийнятті рішень, уміння створювати умови для цілісного сприйняття загальної картини та орієнтуватись в нестандартних ситуаціях

Девіз уроку: «Щоб дійти до мети, треба перш за все йти» Оноре де Бальзак

Актуалізація опорних знань Вправа: «Зарядка для розуму» Логарифм числа b за основою а — це ________________, до якого треба піднести а, щоб отримати b.показник степеняlogab = n, ⇔a >0; a ≠ 1 b > 0; an=b1) Вставте пропущені слова:

Який з виразів є логарифмом числа х за основою а? A) logx a. Б) loga x. В) x lg a Г) lg a x. Актуалізація опорних знань. Вправа: «Зарядка для розуму»2) Виберіть вірну відповідь:style.colorfillcolorfill.type

Актуалізація опорних знань. Вправа: «Зарядка для розуму»а) Логарифм за основою 10 називають_______________ і позначають______. десятковимlg bб) Логарифм за основою e називають _______________ і позначають______.ln bнатуральним(е – ірраціональне число, e ≈ 2,7)  3) Вставте пропущені слова та вирази:

Яка рівність вірна?А) lg 1 =2 Б) ln 1 = e. В) lg 1 100 = - 2 Г) ln 1 𝑒 = 0 Актуалізація опорних знань. Вправа: «Зарядка для розуму»4) Виберіть вірну відповідь:style.colorfillcolorfill.type

Яку з рівностей називають основною логарифмічною тотожністю? А) 𝒙𝒍𝒐𝒈𝒂𝒙=𝒂 Б) 𝒂𝒍𝒐𝒈𝒙𝒂=𝒂 В) 𝒂𝒍𝒐𝒈𝒂𝒙=𝒙  Г) 𝒙𝒍𝒐𝒈𝒙𝒂=𝒙  Актуалізація опорних знань. Пам’ятай!𝒂𝒍𝒐𝒈𝒂𝒃= b Вправа: «Зарядка для розуму»5) Виберіть вірну відповідь:style.colorfillcolorfill.type

Актуалізація опорних знань6)Знайди помилку: 𝟎,𝟑𝟐𝐥𝐨𝐠𝟎,𝟑𝟔= 𝟎,𝟑log𝟎,𝟑𝟔∙𝟐 = 𝟎,𝟑log𝟎,𝟑𝟏𝟐 = 12 Вірно: 𝟎,𝟑𝟐𝐥𝐨𝐠𝟎,𝟑𝟔=  𝟎,𝟑log𝟎,𝟑𝟔𝟐 =  Пам’ятай!𝒂𝒍𝒐𝒈𝒂𝒃= b  𝟔𝟐 = 36 Вправа: «Зарядка для розуму»

Мотивація навчання. Для чого взагалі потрібні логарифми? Яка від них практична користь? Мабуть, найкраще відповів на ці питання знаменитий математик, фізик і астроном П’єр-Симон Лаплас (1749-1827). На його думку, винахід такого показника, як логарифм, немов подвоює життя астрономів, скорочуючи обчислення кількох місяців в працю кількох днів. Деякі на це можуть відповісти: мовляв, любителів таємниць зоряного неба порівняно небагато, а іншим-то людям що дають логарифми? Говорячи про астрономів, Лаплас мав на увазі, перш за все, тих, хто займається складними обчисленнями. А винахід логарифмів дуже полегшив цю роботу.

Отже, логарифми потрібні для спрощення важких обчислювань. Завдяки властивостям логарифмів множення можна замінити простим додаванням, ділення – відніманням, а добування кореня і піднесення до степеню можна перетворити у множення та ділення.

Логарифми в житті людини. Властивості будови слухового апарату людини відповідає властивостям логарифмічної функції. Тому діапазон звуків, що сприяє вухо, низький – від шелесту листя до гуркоту грому. Досліди показали, що організм ніби «логарифмує» отримані ним подразнення, тобто величина відчуття приблизно пропорційна десятковому логарифму величини подразнення. Шкідливий вплив промислових шумів на здоров'я і продуктивність праці робітників спонукало виробити прийоми точної числової оцінки гучності шуму, які опираються на властивості логарифмів.

Логарифми в житті людини. Музиканти рідко захоплюються математикою, хоча зустрічаються з нею набагато частіше, ніж самі про це підозрюють. Вони грають на «логарифмах». І дійсно, так звані ступені частот звукових коливань є логарифми за основою 2.

Під час будівництва ставків необхідно враховувати кількість води, що буде прибувати у ставок у період повені. Розрахунки проводяться за допомогою логарифмів. Логарифми в житті людини

Логарифми в житті людини. У сільському господарстві також не обійшлося без логарифмів. Адже вагу телят одчислюють за допомогою логарифмів.

Відомо, що, консервуючи овочі, важливо знати кислотність розчину, а, знаючи кислотність, можна визначити концентрацію іонів водню. Це можна зробити за допомогою логарифмічних рівнянь, використовуючи десяткові логарифми. Логарифми в житті людини

Об‘єм легенів можна виразити формулою:f(x) = 𝟏𝟏𝟎 (𝒍𝒏𝒙−𝟐)𝒙,Де х – вік людини у роках (х > 10),f(x) - об‘єм легенів у літрах. Розраховано, що найбільший об‘єм легенів має двадцятирічна людина (≈ 5,4 л) Логарифми в житті людини

Властивості логарифмів: Для будь-якого a >0; a ≠ 1; x > 0; y >0 Ці рівності випливають із співвідношень: а0 = 1, а1 = а  1) loga 1 = 0 2) loga a = 1 Наприклад:1) log91 = 0, оскільки 90 = 1;2) log99 = 1, оскільки 91 = 9.

3) Логарифм добутку дорівнює сумі логарифмів множників: Властивості логарифмів: Для будь-якого a >0; a ≠ 1; x > 0; y >0loga (xy) = loga x + loga y. Наприклад: Обчислітьlg(205) = lg100 =2lg 20 + lg5 =

Властивості логарифмів: Для будь-якого a >0; a ≠ 1; x > 0; y >04) Логарифм частки дорівнює різниці логарифмів чисельника і знаменника (діленого і дільника):loga 𝒙𝒚 = loga x – loga y Наприклад: Обчислітьlog1248 – log124 = log12 484 = log1212 =1

(№1) Вправа: Знайди помилку1) log362 + log3618 = log36(2+18) = log3620 Вірно: log362 + log3618 ==log36(2∙18) = log3636 = 12) log1354 – log132 = log13(54-2) = log1352  Вірно: log1354 – log132 =  =log13542 =  log1327 = - 3

5) Логарифм степеня дорівнює добутку показника степеня на логарифм основи: Властивості логарифмів: Для будь-якого a >0; a ≠ 1; x > 0loga x n = n loga x. Наприклад:log381=log334 =loga xn = nloga x4 log33=4loga a = 11

(№2) ЗНО не за горами. Обчисліть значення виразу:log345 + log3900 – log3500 = log3 45∙900500 = = log3 (9∙9) =log381 =log334 =4 log33 =1= 4∙1 =4

Властивості логарифмів: Для будь-якого a >0; a ≠ 1; x > 06) 𝒍𝒐𝐠𝒂𝒑x = 𝟏𝒑 loga x  Наприклад:log82=𝑙𝑜g232 = 𝒍𝒐𝐠𝒂𝒑x = 𝟏𝒑 loga x  13 log22= 13 loga a = 11

(№3) ЗНО не за горами. Обчисліть:𝑙𝑜g1255 =   𝑙𝑜g152512= - 14  1 - 14∙1 = loga xn = nloga x 𝒍𝒐𝒈𝒂𝒑x = 𝟏𝒑 loga x  12𝑙𝑜g5−25= = - 12∙ 12𝑙𝑜g55= 

7) Формула переходу до іншої основи: Властивості логарифмів: Для будь-якого a >0; a ≠ 1; b > 0; c >0; c ≠ 1loga b = 𝒍𝒐𝐠𝒄𝒃𝒍𝒐𝐠𝒄𝒂 Наприклад: Обчисліть: log3264 =65 = Перейдемо до основи 2 за формулою: loga b = 𝒍𝒐𝐠𝒄𝒃𝒍𝒐𝐠𝒄𝒂   𝑙𝑜g2 64𝑙𝑜g232 = 1,2𝑙𝑜g226𝑙𝑜g225 = = 6𝑙𝑜g2 25𝑙𝑜g22 = 

(№4) ЗНО не за горами. Обчисліть: logb a, якщо log3 a = 8, log3 b = 5logb a = 85 = 51,6𝑙𝑜g3 𝑎𝑙𝑜g3𝑏 = Перейдемо до основи 3 за формулою: loga b = 𝒍𝒐𝐠𝒄𝒃𝒍𝒐𝐠𝒄𝒂  8

8) Формула переходу від основи a до b: Властивості логарифмів: Для будь-якого a >0; a ≠ 1; b > 0; b ≠ 1 loga b = 𝟏𝑙og𝒃𝒂 Наприклад: Обчисліть:loga b = 𝟏log𝒃𝒂 =3 𝑙𝑜𝑔37 = 𝒂𝑙og𝒂𝒃= b 73 1𝑙𝑜𝑔73 

(№5) ЗНО не за горами. Обчисліть значення виразу loga500 – loga4,якщо log5a = 14 Розв‘язання:loga500 – loga4 =loga5004 = =loga125 = loga53 = 3loga5 =3 ∙ 1𝑙𝑜𝑔5𝑎 = = 3 ∙ 114 = 3 ∙ 4 =12loga b = 𝟏log𝒃𝒂 𝟏𝟒 

9) loga b ∙ logc d = logc b ∙ loga d. Обчислити: log43∙ lg4∙ log910 =log44∙lg 10∙ log9 3 = 11 = 𝑙𝑜𝑔323 =  12 log3 3 = 112 Властивості логарифмів: Для будь-якого b >0; d > 0; a > 0; a ≠ 1 c >0; c ≠ 1 Наприклад:𝒍𝒐𝒈𝒂𝒑x = 𝟏𝒑 loga x  

(№6) ЗНО не за горами. Обчисліть: log34∙log45∙log57∙log781 == log381∙log44∙log55∙log77 =1111= log334= 4 log33 =4∙1=4

(№7) Пошуковий практикум: (додатково)завдання з демонстраційного варіанту ЗНО 2021 р. Обчисліть значення виразу: 𝑙𝑜g527 𝑙𝑜g52 − 𝑙𝑜g5162 =  = 𝑙𝑜g533𝑙𝑜g52162 = 3 𝑙𝑜g53𝑙𝑜g5181 = 3𝑙𝑜g53𝑙𝑜g53−4 = 3𝑙𝑜g53− 4𝑙𝑜g53 =  = - 34 =  - 0,75

(№8) Пошуковий практикум: (додатково)1) Обчисліть значення виразу: log549 + 2log5 57 2) Знайти значення виразу: 62𝑙𝑜g69− 𝑙𝑜g64 3) Обчисліть 𝑙𝑜g𝑎𝑎𝑏, якщо 𝑙𝑜g𝑎𝑏 = 7 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД𝟐𝟑23𝟕𝟐4{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД234

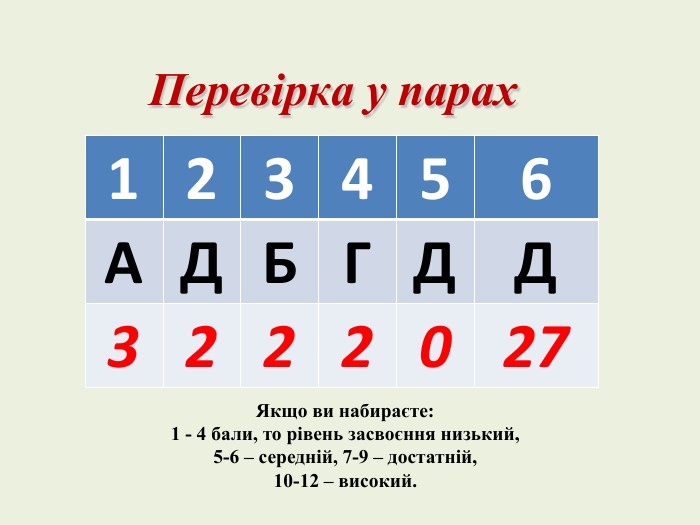
Тест-контроль (кожна вірна відповідь – 2 бали) Якщо ви набираєте 1 - 4 бали, то рівень засвоєння низький, 5-6 – середній, 7-9 – достатній, 10-12 – високий3) lg25lg 5 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД-1215202) Обчисліть: log318 - log32{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД96log316321) Обчисліть: log25 + log21,6{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД33,30,254log2 6,6

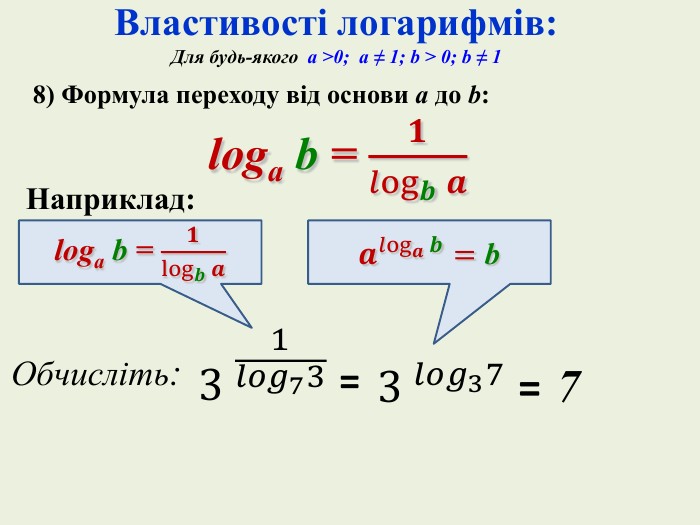
Тест-контроль (кожна вірна відповідь – 2 бали)4) Обчисліть: log95∙log581{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД405451205) Обчисліть: log3𝟓+𝒍𝒐𝒈𝟏𝟑𝟓 6) Обчисліть значення виразу: 𝟐𝟑𝒍𝒐𝒈𝟑𝟐  {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД013227{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД-1log3𝟓1log350{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД-11log350

Перевірка у парах{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}123456 АДБГДД3222027 Якщо ви набираєте: 1 - 4 бали, то рівень засвоєння низький, 5-6 – середній, 7-9 – достатній, 10-12 – високий.

1. Чи задоволений ти своєю роботою на уроці? а) так; б) частково; в) ні; г) важко відповісти2. Яким чином ти збираєшся усунути прогалини? а) спитати у викладача; б) спитати у товариша; в) впораюсь сам (сама); г) не знаю3. Чи зміг би ти пояснити хід розв‘язку задачі своєму товаришу? а) так; б) частково; в) ні; г) важко відповісти4. Якій формі роботи на уроці ти надаєш перевагу? а) индивідуальній; б) у парі; в) колективній Виберіть картинку, що відповідає твоєму настрою на уроці: Рефлексія

Домашнє завдання: Підручник: Математика: (алгебра і початки аналізу та геометрія, рівень стандарту) для 11 кл.\ О. С. Істер № 4.5 (початковий рівень)№4.21 (середній рівень) № 4.38 (достатній рівень) № 4.51 (високий рівень)

Необхідність у складних розрахунках XVI століття швидко зростала. Наприкінці століття декільком математикам, майже одночасно, прийшла у голову ідея: замінити трудомістке множення на просте додавання, а ділення автоматично заменюється на больш просте и надійне віднімання. Чорний ящик №1

Чорний ящик. Тут знаходиться результат діяльності багатьох вчених . Те, що тут лежить, використовувалось у навчальних закладах та інженерних розрахунках до кінця минулого сталіття. Джон Непер. Л. Ф. Магницкий. В. Брадіс. Генрі Бригс

Логарифмичні таблиціppt_x

Тут лежить те, що ще в 20 роках ІV століття придумав англійський математик Уільям Отред.«Рахувати на ній можна швидко, місця майже не займає, її можна всюди носити із собою в кишені»Чорний ящик №2

Логарифмичні лінійки

77log. Знайти значення виразу rbalog=rbalog aalog=1rbalog. Запам’ятай!aalog=144log66log111

Недавно попались на глаза очеловеченные смешные образы уравнений. Ах, как много жизни в этой математике !!! Не правда ли?Копилка приколов репетитора по математике - вибрации

Псевдо математика с Луи де Фюнесом. Псевдо математика с Луи де Фюнесом. Знаменитый французский киношный комик Луи де Фюнес в молодости возможно тоже увлекался математикой. Роль репетитора за 37 лет жизни в кино ему, насколько я знаю, не довелось сыграть, но в каком то фильме в 50-х годах промелькнул забавный эпизод. Луи, с присущей ему безграничной фантазией дурачится у доски, записывая свою трактовку примера на вычисление 66 + 99. Что у него получилось — одному Фюнесу известно.

Как не правы те друзья, что утверждают смело: логарифмы – ерунда, не нужны для дела. Логарифмы – это всё:музыка и звуки, и без них никак нельзя обойтись в науке. Фізика - інтенсивність звуку (децибели). Астрономія – шкала яскравості зірок. Хімія – активність водневих іонів. Сейсмологія – шкала Ріхтера. Теорія музики – нотна шкала по відношенню до частот нотних звуків.Історія – логарифмічна шкала часу.

Розв'язок завдань1. Перевірте правильність рівності:2. Обчисліть:

3. Користуючись основною логарифмічною тотожністю, спростіть вираз: Критерії оцінювання. Кожне завдання оцінюється 1 балом. Якщо ви набираєте 1 - 4 бали, то рівень засвоєння низький, 5-6 – середній, 7-9 – достатній, 10-12 – високий.