Презентація до виступу на тему "Мотивація навчальної діяльності учнів на уроках математики"

Мотивація навчальної діяльності учнів на уроках математики. Учитель: Кодря О. М.

Мотив — це спонукання людини до активності, пов'язане з намаганням задовольнити певні потреби. Внаслідок усвідомлення і переживання потреб у людини виникають певні спонукання до дій, внаслідок яких ці потреби задовольняються.

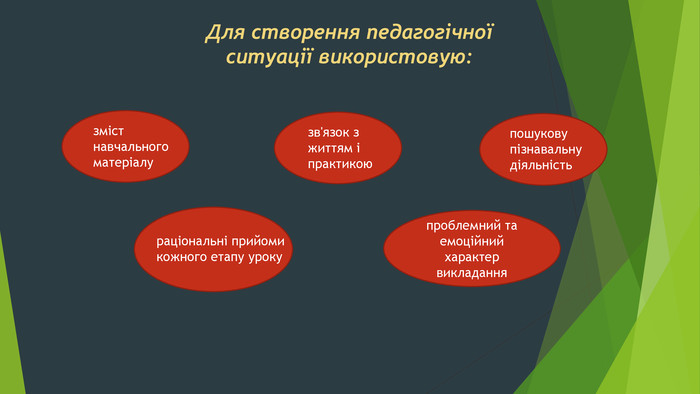
Навчання, підкоряється загальній схемі: Необхідність – початок будь-якою діяльності учня, тобто на уроці висуваються проблеми, які треба розв´язати. Потреба (вивчити новий матеріал або отримати оцінку)Мотив (викликати у дитини бажання займатися проблемою )Мета (ті завдання, які вчитель ставив перед учнями, і які треба виконати за урок)План досягнення мети. Корекція. Оцінка результатів

Давнє прислів’я говорить : «Учитель повинен дати від себе, щоб учень прийшов до себе »

Виділяються три рівні людських здібностей: І рівень- діти здатні взяти все, що їм дають, але не здатні зберегти або зберігають з великими труднощами (здібності нижче середнього); 2 рівень – діти не тільки беруть усе, а й постійно працюючи, спокійно його збільшують(здібності середнього рівня);3 рівня - здібності. Діти не тільки беруть, а й в багато разів збільшують. Це Архімед, Ньютон, Ломоносов… Їхні здібності вище від середнього рівня.

Як кажуть французи: «Всі жанри добрі, крім нудного». Урок повинен бути насичений цікавими фантами, а не тільки містити відомості з підручника та розв,язування задач до теми. Ще Гьоте писав: Пергаменты не утоляют жажды,Ключ у мудрости не на страницах книг,Кто к тайнам мысли рвётся мыслью каждой,В своей душе находит их родник.

Для створення педагогічної ситуації використовую:зміст навчального матеріалузв'язок з життям і практикоюраціональні прийоми кожного етапу урокупошукову пізнавальну діяльністьпроблемний та емоційний характер викладання

Використання:ефекту подивунавчальних дискусійметоду аналізу життєвих ситуаційпізнавальних ігор та ігрових ситуацій. елементів цікавої математикизадач прикладного характерупрактичних задач відкритої інформації на уроках математикиметоду доцільних задачнового математичного фактуісторичного матеріалу. Створення:проблемної ситуаціїситуації зацікавленостіситуації вільного вибору учнями навчального завданняситуації захопленостіситуації успіху А також: евристична бесіда пізнавальні ігри застосування нового математичного матеріалу Способи й методи мотивації:

Для мотивації навчання актуальними є поради:підтримувати рівний стиль стосунків між усіма учасниками навчання підбадьорювати учнів, коли вони стикатимуться з труднощами підтримувати позитивний зворотній зв’язокпіклуватися про різноманітність форм і методів навчанняпривчати учнів до пізнавальної праці, розвивати їх наполегливість, силу волі, цілеспрямованість заохочувати виконання підвищеної складності учити чітко визначати менту, завдання формувати почуття відповідальності та обов’язкуучити висувати вимоги насамперед до самого себе

Пізнавальну діяльність учнів організовую у процесі взаємодії:«учень-інформація»«учень-ситуація», «учень-проблема», «учень – знання», «учень –– знання»«учень– вміння та навички»«учень-учень»«учень-група»

Схематично це виглядає так: {E269 D01 E-BC32-4049-B463-5 C60 D7 B0 CCD2}Індивідуальна самостійна робота учнів за схемою орієнтованої основи дій{E269 D01 E-BC32-4049-B463-5 C60 D7 B0 CCD2}Робота в парах (обговорення й корекція){E269 D01 E-BC32-4049-B463-5 C60 D7 B0 CCD2}Робота в групах (вироблення точки зору, узгодження думок){E269 D01 E-BC32-4049-B463-5 C60 D7 B0 CCD2}Колективна робота (групування думок формування висновків)

Форми інтерактивних технологій:міні-проектинезакінчене реченнярекламаток-шоупрезентаціямікрофонмозковий штурмрольову груматематичний диктант

П’ять груп мотивів навчання:комунікативнісоціальнівідповідальностіперспективипізнавальні

Мотиви перспективи пов’язані зі встановлення Далекої мети навчання. Близької мети навчання. Близьку мету ставить учитель: забезпечення учня методикою оволодіння складними темами навчального матеріалу,поглиблення його знань за рахунок допоміжної літератури, самоосвіти, Факультативних занять

Підласий стверджував: «Потреби, мотиви, стимули – це «ягоди»з одного поля». Його думки стали моїм кредо щодо мотивації навчальної діяльності:- Спираюсь на бажання дитини. Важливе не те, чого бажаємо, а й те, чого хоче учень. Він не впевнений у своїх бажаннях. Завдання вчителя – змінити напрямок його прагнень, якщо вони не збігаються з педагогічними цілями.- Примушую своїх учнів чогось палко забажати. Головне, щоб бажання виникли, а ми змогли б їх використати.- Враховую інтереси й нахили. Розповідаю про те, що цікавить моїх учнів, точніше,з цього починаю. У Важких випадках іду від яскравої форми до зміясту, від емоцій до логіки.- Знаходжу можливість допомогти учням у здійсненні їх намірів.- Заохочую бажання досягти визнання. Не нехтую тим, що багато дітей вчиться не тільки заради знань, а й заради престижу.- Більше хвалю, менше критикую. Авансую найменші позитивні досягнення. «Я вірю що ти зможеш!»- Використовую зовнішню привабливість й цікаві форми роботи, оформлення результатів, кінцевої оцінки діяльності.- Заклик «треба!» трансформую в «це потрібно зробити! Ти ж вольова людина!»- Миттєво використовую ситуацію, що виникла випадково, як стимул.

С. Д. Пуассона писав , що «життя прикрашене двома речами: вивченням математики та її викладанням.»На кожному етапі уроку: використовую відомості про значення математики для сучасних досягнень науки й техніки, залучаю елементи історизму, встановлюю міжпредметні зв’язки, на яскравих прикладах переконую в необхідності конкретних знань для оволодіння певною професією.

«Математику слід вивчати у школі ще й з тією метою, - стверджував М. Лобачевський, - щоб набутих знань було достатньо для звичайних потреб у житті». Тому одним із девізів моєї педагогічної діяльності є слова: Я знаю, нездібних дітей не буває, БОГ кожній дитині дарує талант, І в кожній із них якась здібність дрімає – Політик, поет, слюсар чи музикант.

Фрагменти уроків з елементами мотивації:

Урок – ярмарок у 5 класіТема. Метрична система мір. Вимірювання величин Метою уроку було ознайомити учнів з народними мірами маси і довжини, із мірами часу; закріпити навички перетворення величин; сприяти зацікавленню у поглибленому вивченні математики; розвивати логічне мислення. Досягти мети на уроці я змогла, застосувавши інтерактивні методи «Інсценізація», «Рольова гра». Форма уроку сприяла активізації навчально-пізнавальної діяльності учнів, узагальненню, поглибленню та систематизації їх знань про метричну систему мір.

Урок - подорож у 6 класіТема. Відношення і пропорціїНа даному уроці я використала:- педагогічні прийоми «Приваблива мета», «Дивуй», які зменшили кількість байдужих;- нетипові форми опитування «Кросворд», «Шифрограма», які активізували діяльність учнів на уроці;-інтерактивний метод навчання “Робота в групах”, який дозволив продуктивніше організувати роботу на уроці, згуртувати класний колектив.

Інтегрований урок з алгебри та зарубіжної літератури у 8 класі Тема. Омар Хайям — видатний поет і математик мусульманського Ренесансу. Форма уроку дала мені змогу:- поєднати формування вмінь і навичок учнів розв'язувати квадратні рівняння із узагальненням знань учнів про літературну спадщину О. Хайяма;- розвивати в учнів вміння творчо переносити набуті знання та навички в нові ситуації;- сприяти поглибленню та розширенню знань учнів;- підвести учнів до переосмислення значення даної теми.

Урок-тренінг з алгебри і початків аналізу в 11 класіТема. Розв’язування прикладних задач із застосуванням елементів комбінаторики. Урок був орієнтований на максимальну активність учнів, взаємообмін досвідом, використання групової взаємодії. На даному уроці були використані такі базові методи тренінгового навчання як метод кейсів, моделювання практичних ситуацій, мозкова атака. Активізації діяльності учнів також сприяло використання ІКТ.

Метод проектів: тип - навчальний 5 клас, математика•Тема проекту: цифри, натуральні числа;•Учні об'єднуються у 4 групи.•Мандрівники в минуле: вивчення історії виникнення цифр і чисел; робота з додатковими джерелами інформації; створення усного журналу «цифри та числа»•Дослідники: моделювання проблеми математичною мовою, створення ігрової ситуації, виготовлення наочності (читання чисел), створення презентації «цифри у віршах».•Журналісти: пошук та підготовка цікавих матеріалів про цифри і числа (кросворди, ребуси, загадки), участі у конкурсі «створи казку», створення газети «математичний вісник».•Психологи: підібрати матеріал (тест) на увагу і швидкість реакції. Виявити хто самий уважний.

Метод проектів: тип – дослідницький 9 клас, геометрія урок систематизації знань, вмінь та навичок•Тема проекту: симетрія в житті та творчій діяльності людини•Учасники проекту: учні 9 класу•Мета:дослідити симетрію в житті та творчій діяльності людини; через поняття «симетрія» показати взаємозв’язок між літературою, живописом, архітектурою.•Учні об'єднані у 3 групи•Архітектори: дослідити походження симетрії; навести приклади симетрії в світовій архітектурі,симетрії в дизайні та інтер'єрі; асиметрична композиція.•Письменники: види симетрії в літературних творах,симетричні слова, речення, вірші; приклади фігурних віршів;приклади асиметрії в світових творах;•Мистецтвознавці: симетрія у природі; поняття симетрії з точки зору художника; симетрія в картинах українських художниць; симетрія в кольорі та орнаменті; симетрія в геральдиці та іконописі; симетрія в декоративно-прикладному

Уроці геометрії (10 клас) з теми «Перпендикулярність прямих і площин» можна запропонувати питання практичного змісту , що «спровокує» учнів до активного навчання:1. Як перевірити за допомогою вимірювань, чи є перпендикулярною до підлоги лінія, по якій з’єднуються дві суміжні стіни кімнати?2. Як перевірити за допомогою рулетки вертикальність стовпа?3. Як перевірити вертикальність стержня, користуючись лише прямокутним аркушем паперу?4. Чому льодові бурульки, які звисають з даху навесні, можна вважати паралельними між собою (нехтуючи їхньою товщиною)?5. Чому поверхню стола можна вважати горизонтальною, якщо він стійко стоїть на підлозі, тобто всі його ніжки однакові, торкаються підлоги і розміщені вертикально до неї.6. Чому для встановлення горизонтальної платформи на горизонтальній поверхні досить помістити її на вертикальні опори однакової висоти?7. Щоб переконатись у вертикальності двох стовпчиків, учень перевірив, що перший встановлено вертикально і висоти стовпчиків однакові. Відстані між їх основами та верхівками теж однакові. Чи можна після цього зробити висновок, що й другий стовпчик встановлено вертикально?8. Як на практиці перевірити, чи перпендикулярна площина стіни до площини підлоги?9. Чому висок щільно прилягає до вертикальної стіни, а до похилої – ні?10. Чому поверхня дверей, незалежно від того, зачинені вони чи відкриті, розміщена вертикально до підлоги?

Питання для уроків алгебри 10 клас до теми «Функція»1. Як площа квадрата залежить від його сторони? Задайте формулою цю залежність.2. Маса шматка крейди залежить від його об'єму при сталій густині крейди. Задайте залежність маси т шматка крейди від значення його об'єму V.3. Задайте залежність довжини одного катета прямокутного трикутника від довжини другого катета при сталій гіпотенузі.4. Задайте формулою залежність між опором провідника R і силою струму І, що проходить через провідник при сталій напрузі. Чи задає ця формула функцію?5. Задайте формулою залежність тривалості руху автомобіля між об’єктами А і В. Якою є поведінка швидкості?6. Задайте залежність довжини кола від радіуса кола. По кожному з цих завдань можна запропонувати дослідження властивостей функцій.

Ігрові ситуації

При вивченні теми «Додатні та від’ємні числа» можна використати наступні ігрові моменти:1. Учитель вказує на одного учня, той називає будь від’мне число. Учитель швидко вказує на другого учня, той повинен назвати число, менше першого. Учитель вказує на третього учня, той повинен назвати число, що знаходиться між першими двома. (Тобто більше другого числа, але менше першого). Повторити кілька разів.2. До дошки виходять двоє учнів. Перший називає і записує будь-яке число. Другий називає і записує число, модуль якого більший, ніж модуль першого числа. Перший називає і записує число з ще більшим модулем і т.д. Учні на місцях перевіряють правильність відповідей. Гра припиняється за сигналом вчителя.3. Учитель стоїть обличчям до учнів. Один з учнів записує на дошці будь від’ємне число, більше -33. Учитель стверджує, що, задавши всього чотири питання, відгадає записане число. Сформулювавши перше питання, вчитель вказує на одного з учнів. Той відповідає. Якщо учні не згодні, то руку ніхто не піднімає, і вчитель задає друге питання і т.д. Нехай, наприклад, записане число -3. Учитель задає такі питання: «Це число більше або менше: 1) -16, 2) -8; 3) -4; 4) -2?»

При вивченні теми «Додавання чисел з різними знаками» можуть бути використані наступні ігрові моменти:1. Розставте в квадратиках дев'ять чисел з наступних десяти: -5, -4, -3, -2, 0, 1, 2, 3, 4, 5 - так, щоб сума чисел, що стоять в одному ряду, дорівнювала нулю.2. Гра в -15. Грають парами. На аркуші записано число -15. Перший усно додає до нього одне з чисел 1, 2, 3 і записує суму. Другий усно додає до цього числа одне з чисел 1, 2, 3 і записує суму і т.д. Виграє той, хто запише число 0.3. Задумайте два числа. З першого відніміть друге, результат запишіть. Тепер з другого відніміть перше, результат запишіть. Складіть результати, вийде 0. Чому?

При вивченні теми «Прямокутна система координат на площині. Абсциса і ордината точки» можна використовувати наступні ігри:1. «Попади в ціль»На магнітній дошці малюється система координат. Магнітами до дошки кріпляться «точки» (фігури літаків, танків, підводних човнів або просто умовні кольорові кружечки). Правила гри. Щоб снаряд влучив у ціль, гарматний навідник повинен назвати координати цілі. Перша команда знищує ворожі літаки, друга танки і т.д. Указкою показується фігурка, обраний «навідник» називає її координати, а «гарматний розрахунок» - інші учні цієї команди - «стріляють». Той, хто згоден з названими «навідником» координатами, піднімає зелену картку, а хто ні - червону. Ціль вважається ураженою, якщо всі члени команди дадуть правильну відповідь (фігурка знімається з дошки). Якщо хоча б один учень не згоден з координатами «навідника», фігурка залишається на дошці до з'ясування. Перемагає та команда, у якої кращі «наводчики» і «стрілки».2. «Змагання художників»На дошці записані координати точок. Наприклад: (0, 0), (-1, 1), (-3; 1), (-2, 3), (-3, 3), (-4; 6), (0, 8), ( 2; 5), (2, 11), (6, 10), (3, 9), (4, 5), (3, 0), (2, 0), (1; -7), (3 ; -8), (0; -8), (0, 0). Якщо на координатній площині кожну точку послідовно з'єднати з попереднім відрізком, то в результаті вийде певний малюнок. Дітям ця гра дуже подобається. Можна запропонувати зворотне завдання: намалювати самим будь-який малюнок, що має конфігурацію ламаної, і записати координати вершин

При вивченні теми: «Складання і віднімання додатніх та від’ємних чисел» можна провести дидактичну гру «Фішка». Мета гри - відпрацювати навички додавання і віднімання цілих чисел. А також їх порівняння. Спочатку фішка стоїть на будь клітинці на лінії старту. Учень рухає фішку по таблиці з числами. За один хід за правилами гри він може просунути її на найближчий сусіднє поле по вертикалі або по діагоналі. При переході з однієї клітини в іншу треба додати число, записане в клітині, на яку поставили фішку. Виграє той, хто на лінії фінішу отримає найбільше число. В ході гри школярі, крім обчислень, вчаться вибирати найбільше серед додатніх і від’ємних чисел. Можна скласти таблицю з більш складними завданнями, використовувати дії з звичайними дробами.

При вивченні теми: «Розв’язування лінійних рівнянь» можна провести гру «Математичні ребуси». На дошку для кожної команди проектуються малюнки. Завдання граючим: замість змінних вписати числа, які є коренями рівнянь, записаних по вертикалі і горизонталі. Великий набір діапозитивів або презентація з мультимедійного проектора дає можливість залучити до гри всіх учнів. Виграють ті учні і та команда, які найбільше розгадає ребусів.

При вивченні теми: «Розкриття дужок і внесення в дужки» можна провести гру «Математичний феномен». На початку гри «математичним феноменом» виступає вчитель. Він пропонує кожному з учнів задумати будь-яке число; додати до нього якесь число, помножене на 2, наприклад 8, помножена на 2. знайдену суму розділити на 2, з приватного відняти те число, яке помножили на 2, тобто 8. Учитель вибірково запитує в учнів їх результат і називає задумане ними число. Результат завжди складає половину задуманого числа. Дійсно: (а+2b):2-b = а:2. виграє та команда, яка перша знайде ключ до відгадки і запише її у загальному вигляді. На відміну від ділових ігор, які в більшості випадків займають весь урок, запропоновані дидактичні ігри використовуються лише на окремих етапах уроку, виступаючи у вигляді ігрових моментів і розвивають мотивацію пізнавальної діяльності.

Дякую за увагу!!!