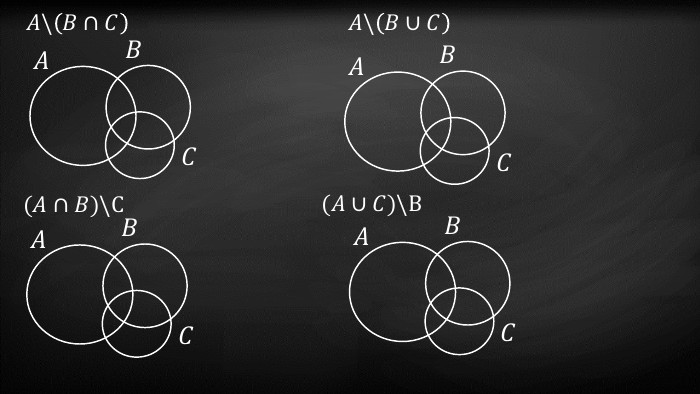
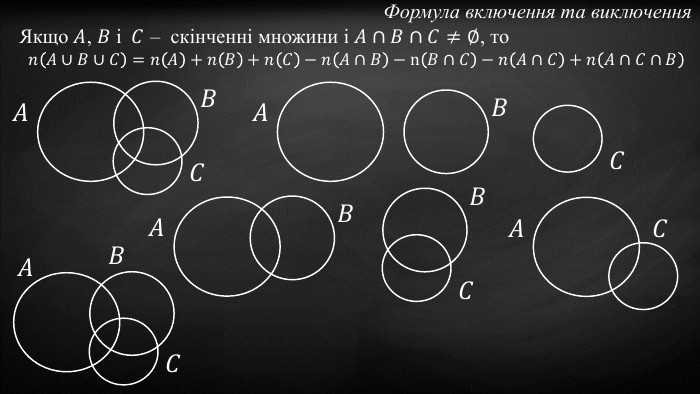
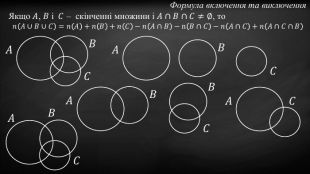
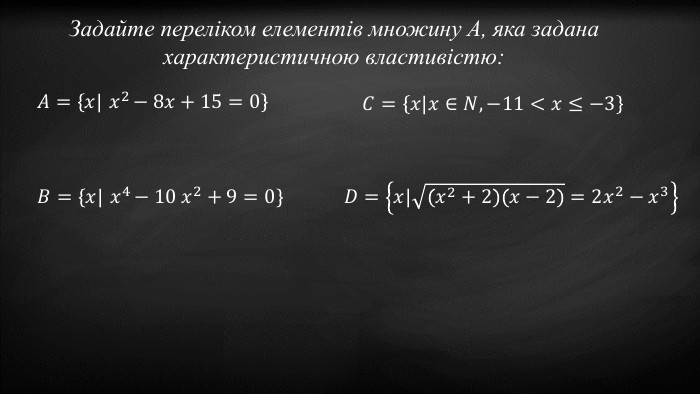Презентація до заняття "Рівнопотужні множини. Формула включення та виключення."
Про матеріал
Презентація до заняття "Рівнопотужні множини. Формула включення та виключення." створена таким чином, щоб вчитель мав можливість пояснюючи теми писати на екрані. Заготовку можна використовувати на уроках алгебри у 8 поглибленому, 10 профільному або ж на заняттях математичного гуртка. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра і початки аналізу (профільний рівень) 10 клас (Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С.)
До уроку
2. Підмножина. Операції над множинами Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку