Презентація "Дотична до кола. Властивості дотичної"
Про матеріал
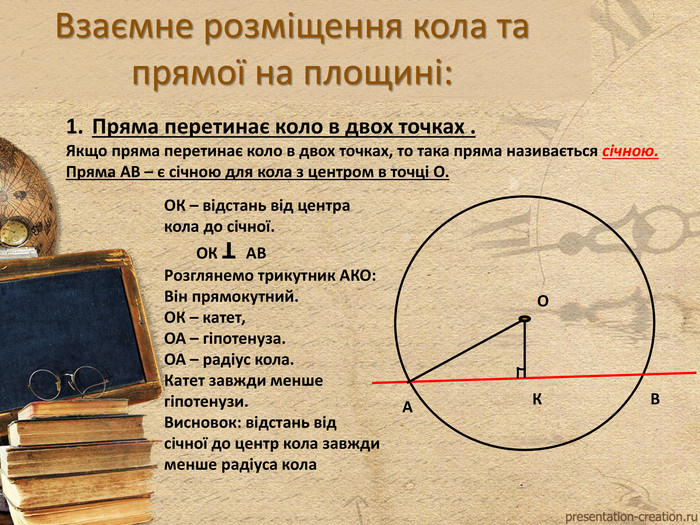
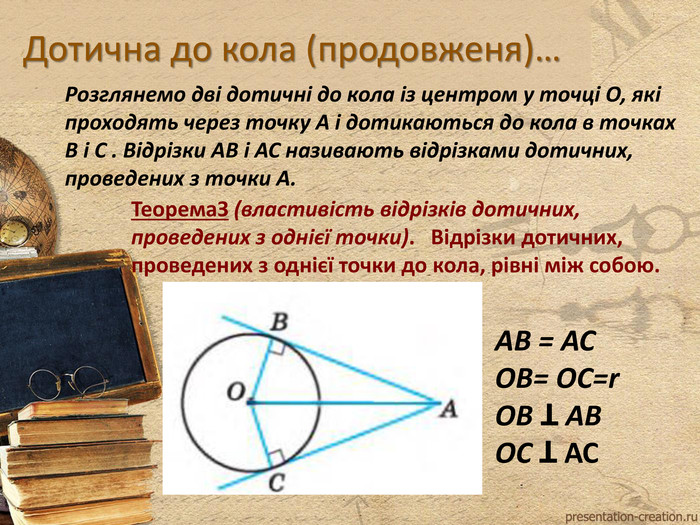
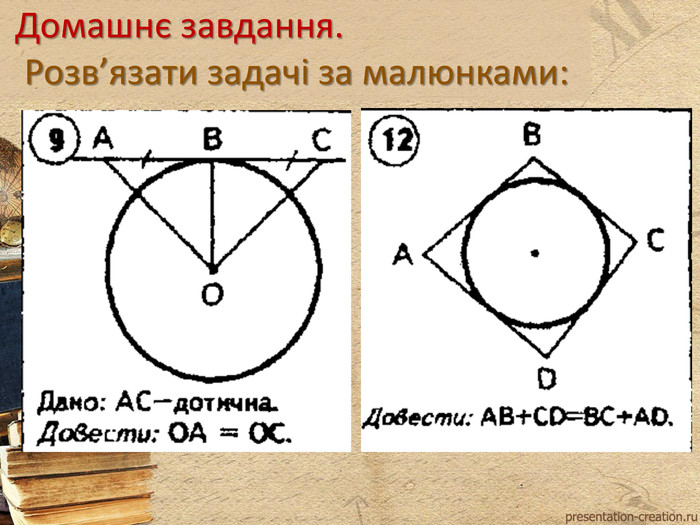
Коло та взаємне розміщення кола та прямої на площині. ВВедення понять "Дотична" та "Січна". Властивості дотичної. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку