Урок " Теорема Піфагора"

Тема « Теорема Піфагора»

Мета  :

Формування  предметних компетентностей:

- домогтися засвоєння теореми Піфагора;

- формувати вміння бачити прямокутні трикутники, які є частинами інших геометричних фігур;

- сформувати вміння знаходити невідому сторону прямокутного трикутника за двома відомими;

Формування ключових  компетентностей:

- формувати вміння оперувати геометричними  фирурами на площині;

- сприяти усвідомленню значення математики для повноцінного життя в сучасному суспільстві;

- сприяти самовихованню допитливості, зацікавленості в пізнанні нового.

Тип уроку: засвоєння нових знань і вмінь.

Обладнання та наочність : підручник, креслярські інструменти,портрет Піфагора, кольорова крейда.

Хід уроку

На дошці розміщено портрет Піфагора  та записано слова «Добре засвоєна мудрість не забувається  ніколи » (Піфагор).

І.Організаційний етап.

Вступне слово вчителя.

Сьогоднішній урок незвичайний. Він пов'язаний зі знаннями, яке виробило людство близько 4000 років.  Дані знання дуже важливі, бо вони допомагали і допомагають людям будувати споруди, які зберігаються тисячоліттями. Це такі споруди, як єгипетські піраміди, храми та інші пам'ятки минулого. Цей урок присвячений одній єдиній теоремі Піфагора, доведенням якої займалися і займаються математики всіх країн. На цей час відомо понад 150 способів доведення теореми Піфагора. Отже , сьогодні ми вивчимо теорему Піфагора та одне з її доведень. Запишіть тему уроку «Теорема Піфагора».
ІІ. Актуалізація опорних знань.

а) Бесіда з класом (за технологією «Мікрофон»):

1. Що таке трикутник?
2. Які є види трикутників?
3. Який трикутник називається прямокутним?
4. Як називаються сторони прямокутного трикутника?
5. Намалюйте на дошці рівнобедрений прямокутний трикутник і назвіть усі його сторони та градусні міри кутів цього трикутника.

б) Виконання усних вправ:

1.Обчисліть:5²; 3²;12²;4²;8²;10².

2.Обчисліть:√25; √16; √9; √144;√100; √400.

3. Знайдіть суму квадратів чисел: 3і 4; 6 і 8; 16 і 12; 5 і 12.

ІІІ. Вивчення нового матеріалу.

а)Історична довідка( готують учні)

1.Теорема Піфагора- одна з визначних теорем математики. Вона  має багату історію. Ще задовго до Піфагора теорема  була відома єгиптянам, вавілонянам, китайцям та індійцям. Доведення самого Піфагора до нас не дійшло. В наш час є більше 150 різних доведень теореми Піфагора. Можливо, що одне з них належить Піфагору чи його учням.

Теорема Піфагора чудова тим, що вона зовсім не очевидна. Із простого спостереження  прямокутного трикутника не зробиш висновок, що між його сторонами є таке просте співвідношення a² + b² =  c². Але це співвідношення стає очевидним, якщо вдало побудувати малюнок.

2. Цього міцного юнака з товстою шиєю та коротким носом, справжнього забіяку, судді однієї з перших олімпіад не хотіли допускати до змагань, тому що Піфагор був малий на зріст. Але йому вдалося побитися зі своїми супротивниками та ще й перемогти.  За деякими даними, Піфагор народився близько 580 р. до н.е. у Стародавній Греції на острові Самос, а помер у 500 р. до н. е.

    Про життя вченого відомо небагато, але з його ім'ям пов'язаний ряд легенд. Розповідають, що він багато подорожував, був у Індії, Єгипті, Вавилоні, вивчав стародавню культуру й досягнення науки різних країн. У м. Кротон,на півдні Індії,він заснував наукову школу - так званий піфагоровський союз.

У школу приймали з великими почестями після випробувань. Кожен, хто приходив у школу, відмовлявся від свого майна й обіцяв зберігати в таємниці вчення засновника. Так на півдні Італії, що була на той час грецькою колонією, виникла так звана Піфагорійська школа. Ті, хто хотів потрапити до неї, повинні були мовчати протягом п'яти років, тільки після цього їх зараховували. Та, незважаючи на незвичайний і жорстокий іспит, багато хто прагнув потрапити до цієї школи. Піфагорійці займалися математикою, філософією, природничими науками й теорією музики. Вони багато винайшли в арифметиці й геометрії. У школі існував декрет, за яким авторство усіх математичних робіт присвоювалося Піфагору. За однією з версій він був убитий під час народного повстання,а будинок школи зруйновано. Після його смерті учні оточили ім'я свого вчителя різноманіт-ними  легендами. Тому встановити правду про звички й характер Піфагора неможливо.

б)Теорема Піфагора.

1.Намалюйте прямокутний трикутник . На  кожній стороні прямокутний трикутник побудуйте квадрат. Знайдіть площу кожного  квадрата та суму площ квадратів побудованих на катетах порівняйте з площею квадрата побудованого на гіпотенузі. Зробіть висновок.( Площа квадрата,побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі квадратів площ побудованих на катетах).

2.Запишемо у вигляді формули c²=a²+b²( де c-гіпотенуза;  a-катет;b-катет).

Сформулюйте теорему Піфагора. «У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів».

3.Розглянемо доведення теореми за підручником(М.І. Бурда,Н.А. Тарасенкова) ст.110.

4.Застосування теореми Піфагора до обчислення невідомої сторони прямокутного трикутника за двома відомими.

Нехай a і b-катети прямокутного трикутника, c -його гіпотенуза. Тоді: a² = c²  - b²; a=;  b²= c²- a², b=.

Правильною є і теорема обернена до теореми Піфагора: якщо квадрат сторони трикутника дорівнює сумі квадратів двох інших його сторін, то цей трикутник – прямокутний.

Наприклад трикутник зі сторонами 3см,4см, 5см – прямокутний (3²+4²=5²). Такий трикутник називається єгипетським.

ІV. Засвоєння нових знань і вмінь.

а) Робота з підручником. Ст.113 вправи усно №728,729.

Б) розв’язування задач за готовими малюнками

  1.Знайти АВ, АС=16см, ВD=6см.               2.Знайти периметр прямокутника.

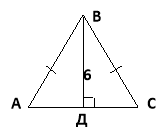
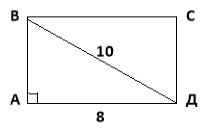
(Відповідь: 10см.)                                         (Відповідь:28см)

В)Розв’язування практичних  задач. (Робота в парах)

1. Дах будинку має форму рівнобедреного трикутника ( ABC) , AB= 50м ,основа трикутника AC = 96 м . Знайти висоту даху. (Відповідь:14 метрів)

2.Висота новорічної ялинки 8 м. Для закріплення її у вертикальному положенні від вершини ялинки зробили натяжки АВ, АC, АD однакової довжини і закріпили їх на підлозі на відстані 6 м від основи ялинки. Якої довжини повинна бути натягуюча проволока, щоб  ялинка стояла вертикально? (Відповідь: 10метрів)

V.  Домашнє завдання.

1. Завдання за підручником. Ст.113.№733,736,№738(а,б), §15.

2. Додаткове завдання.

Сторона квадрата дорівнює 5см. Знайдіть його діагональ.

Складіть « Сінквейн  до прикметника трикутник»

VІ. Підсумки уроку.

Гра «Так — Ні».

Правила гри: якщо твердження здається вам правильним, то покажіть знак плюс, якщо ні  то  знак мінус.

Чи вірите ви, що:

1) будь-який прямокутний трикутник називається єгипетським; (Ні.)

2) Піфагор брав участь у кулачному бої на Олімпійських іграх; (Так, він був чемпіоном у цьому виді спорту.)

3) Фалес був уболівальником і помер на трибуні Олімпійського стадіону під час бою Піфагора; (Так.)

4) якщо кожного дня по 10 годин просто переписувати праці Леопарда Ейлера, то не вистачить і 76 років, щоб переписати їх; (Так, його праці надруковані у 75 великих томах.)

5) Шарль Перро, автор казки про дівчинку у червоному капелюшку, написав казку «Кохання циркуля і лінійки»; (Так.)

6) Наполеон Бонапарт писав математичні роботи; (Так, відома задача Наполеона.)

7) два в квадраті — 4, три в квадраті — 9, кут у квадраті 90⁰; (Так.)

8) Піфагор першим розробив математичну теорію музики; (Так.)

9) Чи вірите ви, що теорему Фалеса назвали «міст віслюка»?

(Не вірю. Так називали теорему Піфагора. А учнів, які вчили її напамять без розуміння, називали)

 10.Чи віриш ти, що існує 25 способів доведення теореми Піфагора? (Ні, понад 150 способів.) 

11.Чи віриш ти, що Піфагор до своєї школи активно залучав жінок тому, що вважав, що вони більш здібні до математики, ніж чоловіки?  (Ні.)