Презентація "Елементи комбінаторики"

Навчальний проект Для учнів 7(11) класу Вчитель Турко О.Г. Первомайська гімназія Елементи комбінаторики

Формування в учнів первинних імовірнісних уявлень; Отримання знань про комбінаторику; Оволодіння вміннями вирішувати задачі; Складання задач, пов’язаних з конкретною життєвою ситуацією; Мета:

Етапи проектної діяльності

І ЕТАП Передпроектна підготовка Формування проектних груп: Перестановки Розміщення Комбінації Біном Ньютона Визначення проблемної мети Розробка плану дослідження Пошук джерел інформації Дослідження історичних даних

ІІ ЕТАП Дослідницький етап Систематизація та узагальнення матеріалу Вивчення основних законів комбінаторики та розв’язування задач з даної теми Комп’ютерне моделювання Складання власних задач Оформлення результатів дослідження та підготовка до підсумкового звіту

ІІІ ЕТАП Презентація отриманих результатів Виступ-захист кожної групи Представлення міні-підручника Презентація особистих досягнень (портфоліо) учнів, одержаних в результаті освітньої діяльності

Історія виникнення комбінаторики XVI століття (азартні ігри) XVIІ століття Н.Тарталья – італійський математик (різні комбінації під час гри) Блез Паскаль, П. Ферма – французькі вчені (теоретичне дослідження) Я.Бернуллі, Л.Ейлера (подальший розвиток комбінаторики) XVIІІ століття

Комбінаторика розділ математики, в якому розглядаються властивості сполук (комбінації, розміщення, перестановки)

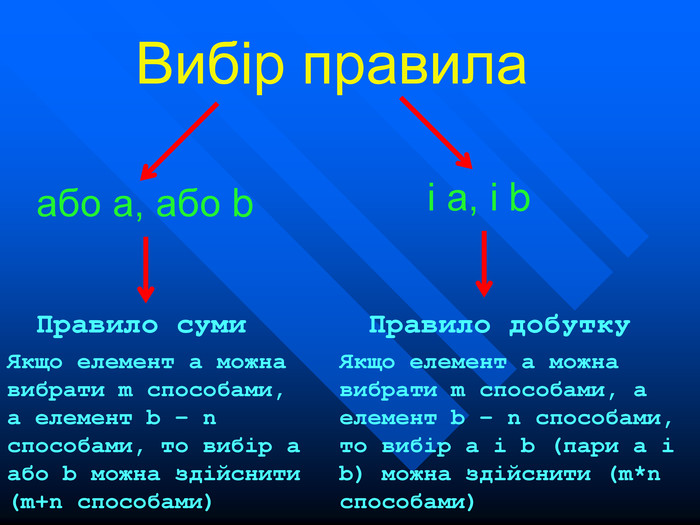
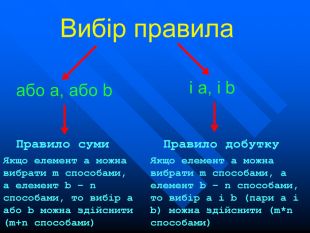
Вибір правила або а, або b і а, і b Правило суми Якщо елемент а можна вибрати m способами, а елемент b – n способами, то вибір а або b можна здійснити (m+n способами) Правило добутку Якщо елемент а можна вибрати m способами, а елемент b – n способами, то вибір а і b (пари а і b) можна здійснити (m*n способами)

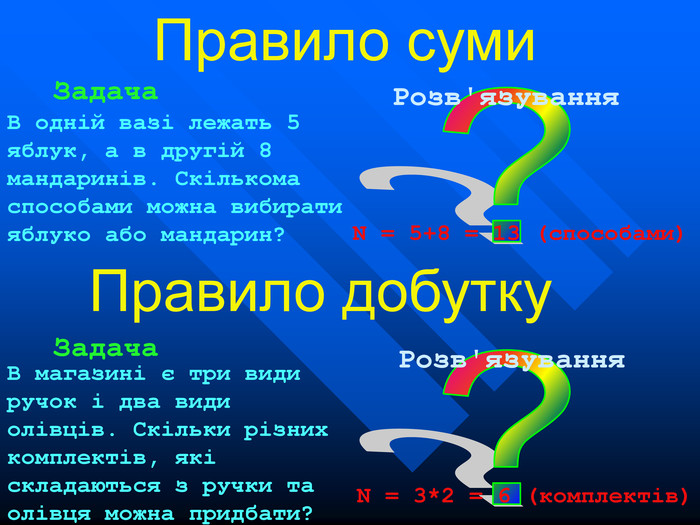
Правило суми Задача В одній вазі лежать 5 яблук, а в другій 8 мандаринів. Скількома способами можна вибирати яблуко або мандарин? Розв'язування N = 5+8 = 13 (способами) Правило добутку Задача В магазині є три види ручок і два види олівців. Скільки різних комплектів, які складаються з ручки та олівця можна придбати? Розв'язування N = 3*2 = 6 (комплектів)

Вибір формули Чи враховується порядок розміщення елементів Чи всі елементи входять у сполуку? Розміщення An m = n! (n-m)! An m = n(n-1)…(n-m+1) Комбінації Cn m = n(n-1)…(n-m+1) 1*2*…*m n! (n-m)!m! Cn m = Перестановки Pn = n! так так ні ні

Група Перестановки

Перестановкою з n елементів називається будь-яка впорядкована множина, яка складається з n елементів. Число перестановок з n елементів позначається Pn Формула Pn = n! n! = 1 • 2 • 3 … (n -1) • n Характеристичні ознаки предмети різні всі місця зайняті порядок елементів важливий

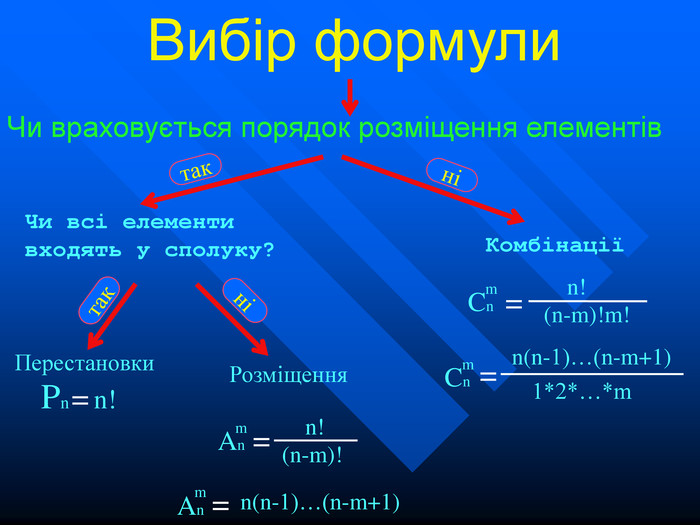
У класі навчається 10 юнаків. Скількома способами можна їх вишикувати у шеренгу? Р10 1*2*....*9*10 = 10! Скількома способами можна скласти список із 9 прізвищ? Скількома способами можна розкласти 8 різних листів у 8 різних конвертів, якщо в кожний конверт кладеться лише 1 лист? Р9 = 9! 1*2*....*8*9 = 362880 Р8 = 8! 1*2*....*7*8 = 40320 Задачі

В класі біля стола кожної групи стоїть 6 стільців. Скільки існує способів розміщення за столом 6 учнів? Р6 =6! Р6 = 1•2•3 •4• 5• 6 = 720

Група Розміщення

Розміщенням з m елементів по n називається будь-яка впорядкована підмножина з n елементів даної множини М, яка містить m елементів, де n  m. Число розміщень з m елементів по n позначається Am n Обчислюються за формулою: Am n = m(m - 1)(m - 2) …(m – n +1) Am n m! = (m-n)!

Характеристичні ознаки розміщень предмети і місця різні 0 ≤ n ≤ m усі n місць необхідно зайняти порядок елементів важливий

Учню треба скласти 4 екзамени …

Учню треба скласти 4 екзамени на протязі 8 днів. Скількома способами це можна зробити? 10 спортсменів розігрують одну золоту, одну срібну і одну бронзову медалі. Скількома способами ці медалі можуть бути розподілені між спортсменами? У класі з 32 учнів для проведення зборів обирають голову, заступника і секретаря. Скількома способами це можна зробити? Задачі A8 4 8х7х6х5 = 1680 = A10 3 = 10х9х8 =720 A32 3 = 32х31х30=29760

В кінці семінару 25 студентів обмінялися фотографіями так, що кожний обмінявся з кожним. Скільки було роздано фотографій? A25 2 = 600 = 25*24

В 11 класі вивчається 14 предметів інваріантної складової. Скількома способами можна скласти розклад занять на понеділок, якщо в цей день повинно бути 6 різних уроків? A14 6 = 2 162 160 = 14• 13 • 12 • 11 • 10 • 9 Розклад

Група Комбінації

Комбінацією з m елементів по n називається будь-яка підмножина з n елементів даної множини М, яка містить m елементів Число комбінацій з m елементів по n позначається Cm n Cm n 1 • 2 • 3 … (n -1) • n m(m - 1)(m - 2) …(m – n +1) = Cm n m! n!(m-n)! =

Характеристичні ознаки порядок вибору елементів не має значення 0 ≤ n ≤ m предмети різні

Основні властивості комбінацій Cm 0 Cm n Cm 2 Cm 1 2 n + + + + … = Cm n = Cm-1 n-1 Cm-1 n + Cm n = Cm m-n Cm n+1 = Cm n m-n n+1

Запишемо всі можливі значення (m = 0, 1, 2, ..., n = 0, 1, 2, ... m) у вигляді трикутної таблиці: Cm n C1 0 C0 0 C1 1 C2 0 C2 1 C3 0 C2 2 C3 1 C3 3 C3 2 C4 1 C4 0 Cn 2 Cn 1 Cn n-1 Cn 0 C4 4 C4 3 C4 2 Cn n … … … … … … … … … … … … …

Трикутник Паскаля 1 1 1 1 1 1 1 1 1 1 1 1 1 2 3 3 4 4 6 6 6 5 5 10 10 15 15 20

Комбінації

Для проведення іспиту створюється комісія із двох викладачів. Скільки різних комісій можна скласти із п’яти викладачів? Із 20учнів треба виділити 6 для чергування. Скількома способами це можна зробити? На полиці є 35 книжок. Скількома способами можна вибрати дві із них? Задачі C5 2 5!:(2! 3!) = (5 • 4) : 2 = 10 = C20 6 = 20! : (6!14!) = (15•16•17•18•19•20) : (1•2•3•4•5 •6) = 38760 C35 2 = 35! : ( 2! 33!) = (35 • 34): 2 = 595

25 студентів потиснули один одному руки перед семінаром. Скільки було зроблено рукостискань? С25 2 = 300 = 25!/2! 23! = 24•25/2

Група Біном Ньютона

Формула бінома Ньютона (a+b) n = Cn 0 * a n + Cn 1 a n-1 * * b + … + Cn m a n-m * * b m + … + Cn n * b n 1 1 1 1 1 1 1 1 1 1 1 1 1 2 3 3 4 4 6 6 6 5 5 10 10 15 15 20 Коефіцієнти розкладу (a+b) збігаються з n-м рядком трикутника Паскаля n

114=14641 14641 (a+b)4=1a4+4a3b+6a2b2+4ab3+1b4 n = 4 113=1331 1331 (a+b)3=1a3+3a2b+3ab2+1b3 n = 3 112=121 121 (a+b)2=1a2+2ab+1b2 n = 2 111=11 11 (a+b)1=1a+1b n = 1 110=1 1 (a+b)0=1 n = 0

Біном Ньютона

Задачі (x+a) 7 0,97 5  0,659

Рефлексія

Яка Ваша думка щодо основної функції теорії комбінаторики? Охарактеризуйте свій емоційний стан протягом та в кінці уроку Які пізнавальні процеси були задіяні на уроці найбільше? Розвитку яких рис характеру сприяв урок? Якого життєвого досвіду ви досягли?