Урок з теми "Розв'язування задач на використання комбінацій (без повторень), розміщень (без повторень), перестановок (без повторень)))"

 

Тема уроку:   

 

Розв’язування задач

на використання комбінацій (без повторень), розміщень (без повторень),

перестановок (без повторень)

 

 

Мета уроку:

• дидактична: ознайомлення учнів з прийомами і методами розв’язання прикладних задач,
• розвиваюча: розвивати в учнів логічне мислення, процеси аналізу і синтезу;
• виховна: виховувати наполегливість і почуття своєї вагомості в колективі, любов до математики

 

Обладнання: мультимедійний проектор, дошка, роздаткові картки

Тип уроку: закріплення вивченого матеріалу

Методи і прийоми: «Робота в малих групах», усне опитування, алгоритм-таблиця, «Мікрофон»

Очікувані результати:  після уроку учні зможуть:

• дати означення:

•            комбінації (без повторень),
•            перестановки (без повторень),
•            розміщення (без повторень);

• записати формули для обчислення комбінацій (без повторень), розміщень (без повторень), перестановок (без повторень);

• розв’язувати задачі на використання правила суми, правила добутку, комбінацій (без повторень), розміщень (без повторень), перестановок (без повторень)

Хід уроку

 

І Організаційний момент (3 хв.)

 

Вступне слово.  

- Добрий день. Сідайте, будь ласка. Поки ви готуєтесь до уроку, налаштовуєтесь на роботу, я відмічу відсутніх. Чергові будь ласка, перевірте готовність дошки до роботи.

- Тема нашого уроку «Розв’язування задач на використання комбінацій (без повторень), розміщень (без повторень), перестановок (без повторень)». Мета уроку: ознайомлення з різними прийомами і методами розв’язання комбінаторних задач. Після уроку ви зможете:

• дати означення:

•            комбінації (без повторень),
•            перестановки (без повторень),
•            розміщення (без повторень);

• записати формули для обчислення комбінацій (без повторень), розміщень (без повторень), перестановок (без повторень);

• розв’язувати задачі на використання правила суми, правила добутку, комбінацій (без повторень), розміщень (без повторень), перестановок (без повторень).

- І першим етапом уроку буде перевірки домашнього завдання.

 

ІІ Перевірка домашнього завдання (5 хв.)

 

- Домашнім завданням було:

Домашнє завдання

повторити: • означення:            комбінації (без повторень),            перестановки (без повторень),            розміщення (без повторень); • правило суми та правило добутку; 2.  розв’язати вправи № 113, 116 стор. 206 (підручник) 3*.  розв’язати рівняння:

 

- Теоретичну частину ми перевіримо через декілька хвилин.

- Для перевірки письмового завдання обміняйтесь, будь ласка, зошитом з сусідом за партою. Ваше завдання: перевірити наявність та правильність виконання задач. Даю вам 3 хвилини. Увага на дошку.

 

Розв’язання домашніх вправ

Вправа № 113 Оскільки з аксіомою І через дві точки можна провести лише одну пряму, то число п усіх прямих дорівнює числу комбінацій із 10 по 2, тобто                      п= Відповідь: 45   Вправа № 116 Оскільки обидві жінки увійдуть до списку, число всіх випадків дорівнює кількості вибору з 30-2=28 (співробітників) двох чоловіків: Відповідь: 378   Розв’язання рівняння : , х є N, 0<х7, , Оскільки 7!0, то можна обидві частини рівності поділити на це число: , тому можемо обидві частини рівності поділити на це число. 8-х=х, х=4. Перевірка. Відповідь: 4

 

- Які є запитання щодо розв’язків задач домашнього завдання?

 

ІІІ Актуалізація вивченого матеріалу (7 хв.)

 

- Наступним етапом уроку буде перевірка теоретичних знань. Я буду задавати питання, а бажаючі будуть відповідати.

 

Усне опитування:

• Дати означення: 1) комбінацій (без повторень)

2) розміщень (без повторень)

3) перестановок (без повторень)

• Сформулювати правило суми

• Сформулювати правило добутку

• Розв’язати задачу (усно). Скількома способами можна вибрати 2 олівці з 12?

(Відповідь: )

• Розв’язати задачу (усно). У вазі стоїть 10 червоних і 5 рожевих  пронумерованих гвоздик. Скількома способами можна вибрати з вази 3 квітки?

(Відповідь: )

• Розв’яжіть рівняння:

(Відповідь: 10)

- Ваші відповіді говорять про те, що теоретичний матеріал кожен з вас знає на достатньому рівні. А зараз перевіримо, наскільки добре ви вмієте розв’язувати задачі, працюючи в невеликих групах і використовуючи знання до розв’язування різних комбінаторних задач. 

 

ІV Закріплення та осмислення вивченого матеріалу (13 хв.)

 

«Робота в малих групах»

- У кожного з вас на парті лежить невеликий кольоровий папірець (всього                5 кольорів). Таким чином з усіх учнів ми утворюємо «5 малих груп».

- Будь ласка, пересядьте кожен в свою групу: червоний колір, жовтий колір, синій колір, зелений колір, фіолетовий колір.

- Перед тим, як кожна група отримає завдання, пригадайте, як працювати в «малих групах» (див. пам’ятку) і розподіліть ролі. 

- Увага! Кожна група отримує картку із завдання. На виконання завдання відводиться 5 хвилин.

 

Картка № 1

Задача. У вазі лежить 10 яблук і 3 груші. Скількома способами можна вибрати один фрукт? Скількома способами можна вибрати два фрукти – яблуко і грушу? Скількома способами можна вибрати яблуко і грушу, якщо вже вибрано один фрукт?

 

Картка № 2

Задача. У класі 16 хлопців і 12 дівчат. 1. Скількома способами можна вибрати одного учня? Скількома способами можна вибрати двох учнів – хлопця і дівчину? Скількома способами можна вибрати хлопця і дівчину, якщо вже вибрано одного учня?

 

 

Картка № 3

Задача. У футбольній команді 11 основних і 8 запасних гравців. Скількома способами можна вибрати одного гравця? Скількома способами можна вибрати двох гравців – основного і запасного? Скількома способами можна вибрати основного і запасного гравця, якщо одного вже вибрано?

 

 

Картка № 4

Задача. У ящику лежить 7 білих і 9 чорних кульок. Скількома способами можна вибрати одну кульку? Скількома способами можна вибрати дві кульки – чорну і білу? Скількома способами можна вибрати білу і чорну кульки, якщо вже вибрано одну кульку?

 

 

Картка № 5

Задача. У взводі 20 солдат і 5 сержантів.   Скількома способами можна вибрати одну людину?   Скількома способами можна вибрати двох людей – солдата і сержанта?   Скількома способами можна вибрати сержанта і солдата, якщо одну людину вже вибрано?

 

- Час вичерпаний. Запрошую до дошки доповідача.

- Поясни, будь ласка, як ваша група розв’язувала задачі, які правила ви використовували?

- Так як задачі для всіх груп були аналогічними, прошу вас перевірити свої розв’язки. Увага на дошку!

Відповіді до задач
Картка № 2   1. Хлопця можна вибрати=16 способами, дівчину - =12 способами. Тому або хлопця, або дівчину можна вибрати 16-12=28 способами → правило суми. 2.   16∙12=192 способами → правило добутку 3. а) Якщо вибрали хлопця, то залишилось 15 учнів, отже, для хлопців є 15 варіантів вибору, для дівчат 12. всього 15∙12=180 способів, б) Якщо вибрали дівчину, то залишилось 11 учнів, отже, для дівчат є 11 варіантів, для хлопців 16. всього 16∙11=176 способів в) 180+176=356 способів → правило суми	Картка № 1 13 способів 30 способів 47 способів
	Картка № 3 19 способів 88 способів 3.  157 способів
	Картка № 4 16 способів 63 способи 110 способів
	Картка № 5 25 способів 100 способів 175 способів

 

- Чи є такі групи, які отримали неправильну відповідь?

 

Колективна робота (10 хв.)

 

Слово вчителя:

- Комбінаторика – розділ математики, в якому розглядаються комбінаторні задачі, тобто такі, в яких є комбінації, розміщення й перестановки (одним словом - сполуки).

- Щоб вибрати ту чи іншу формулу для розв’язування задачі, необхідно з’ясувати, чи враховується порядок розміщення елементів. Якщо так, то чи всі елементи входять у сполуку. Маємо два випадки: Р_т – якщо так, - якщо ні. Якщо ні, то маємо .

- Вибір формули для розв’язання комбінаторних задач можна записати за допомогою такого алгоритму-таблиці (див. додаток). Увага на дошку!

- Запропоновані завдання будемо розв’язувати усно, але пояснювати вибір формули.

 

Завдання:   Визначити вид сполуки, вибрати відповідну формулу для розв’язування задачі
1. Десять друзів при зустрічі потиснули один одному руки. Скільки було зроблено рукостискань?
а) Р10	б)	в)	г)	д)
2. Десять друзів обмінялися фотокартками так, що кожен обмінявся з кожним. Скільки було роздано фотокарток?
а) Р10	б)	в)	г)	д)
3. У класі, де 30 учнів, вибирають команду з 5 учнів для участі у турнірі. Скільки існує варіантів вибору?
а) Р5	б) Р30	в) Р25	г)	д)
4. У класі, де 30 учнів, вибирають команду з 5 учнів: один – капітан команди, по учню – для участі у різних конкурсах. Скільки існує варіантів вибору?
а) Р5	б) Р30	в) Р25	г)	д)
5. Біля столу стоять 4 стільці. Скільки існує способів розміщення за столом чотирьох осіб?
а)	б) Р4	в)	г)	д)

 

- Наступну задачу будемо розв’язувати письмово

 

Задача. У вазі 12 білих і рожевих пронумерованих гвоздик. Відомо, що букет із двох білих і однієї рожевої гвоздики можна скласти 105 способами. Скільки у вазі гвоздик кожного кольору?

Розв’язання

Нехай у вазі х білих гвоздик, тоді рожевих – (12-х). Зрозуміло, що 2≤х≤11. Букет можна скласти способами. Тоді       =105,

;

х∙(х-1)∙(12-х)=210;

12х²-12х-х³+х²-210=0;

х³-13х²+12х+210=0;

х³-6х²-30х-7х²+42х+210=0;

х∙(х²-6х-30)-7∙(х²-6х-30)=0

(х²-6х-30)∙(х-7)=0

х²-6х-30=0     або      х-7=0

х=3                    х=7

3, отже х=7.

Значить, 7 білих і 5 рожевих гвоздик.

Відповідь: 7 білих і 5 рожевих гвоздик.

 

V Підбиття підсумків, оцінювання результатів уроку (5 хв.)

 

- Давайте ще раз пригадаємо основні властивості сполук

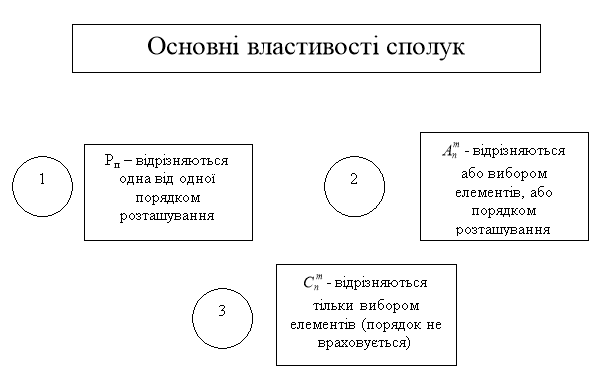
«Мікрофон»

- Чи була корисною сьогоднішня робота і чого ви навчилися?

- Чи досягли ми очікуваних результатів?

- Які труднощі виникли у вас на уроці?

 

- А зараз будемо оцінювати роботу кожного учня на уроці (виставлення оцінок).

 

VІ Домашнє завдання та інструктаж до нього (2 хв.)

 

Домашнє завдання

повторити § 34 стор. 193-206, розв’язати вправи № 115, 119* стор. 206 3.  Задача. У колоді 36 карт, із них 4 тузи. Скількома способами можна вибрати 6 карт так, щоб серед них було 2 тузи?

 

Пам’ятка

 

Як працювати в малих групах

 

Робота в малих групах дасть змогу вам набути навичок спілкування та співпраці

Після того як вчитель об’єднав вас у малі групи і ви отримали завдання, ваша група за короткий час (3-5 хв.) повинна виконати це завдання та представити результати роботи своєї групи.

 

1. Швидко розподіліть ролі в групі: керівник групи, посередник, секретар, доповідач.

 

Керівник групи:

• зачитує завдання;

• організовує порядок виконання;

• пропонує учасникам групи висловитись по черзі;

• заохочує групу до роботи;

• підбиває підсумки роботи;

• за згодою групи визначає доповідача.

Секретар:

• веде коротко і розбірливо записи результатів роботи своєї групи;

• як член групи має бути готовим висловити думку групи при підбитті підсумків або допомогти доповідачеві

Посередник:

• стежить за часом;

• заохочує групу до роботи.

Доповідач:

• чітко висловлює думку, до якої дійшла група;

• доповідає результати роботи групи.

 

2. Починайте висловлюватися спочатку за бажанням, а потім по черзі.

 

3. Дотримуйтесь правил активного слухання, головне – не перебивайте один одного.

 

4. Обговорюйте ідеї, а не особи учнів, які висловили цю ідею.

 

5. Утримуйтесь від оцінок та образ учасників групи.

 

6. Намагайтесь дійти спільної думки, хоча в деяких випадках може бути особлива думка і вона має право на існування.