Презентація "Елементи комбінаторики"
Про матеріал
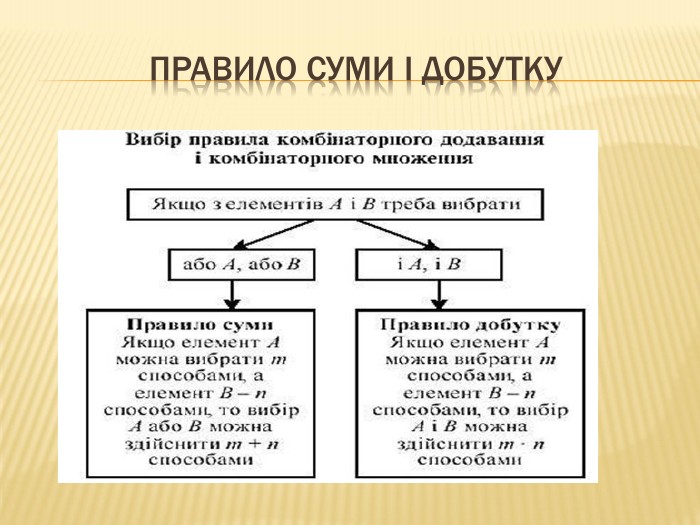
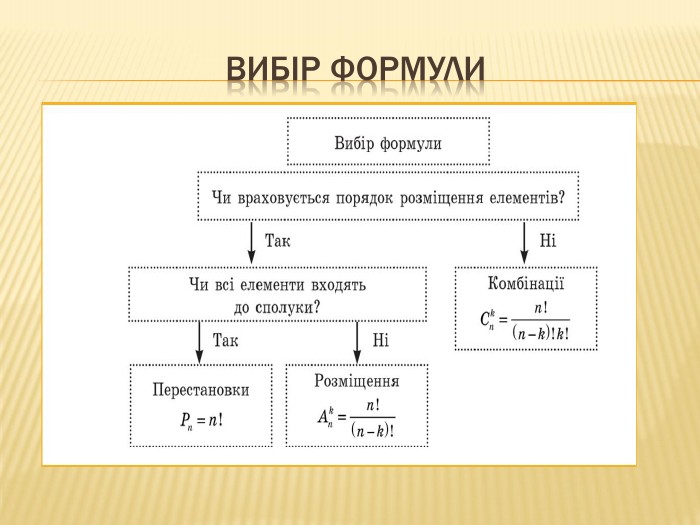
Презентація містить матеріал з теми "Елементи комбінаторики" , який можна використати під час вивчення теми, при підготовці до контрольної роботи з теми, для повторення та підготовки до ДПА та ЗНО з математики Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку