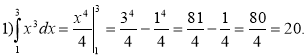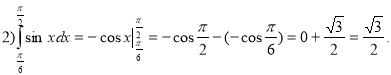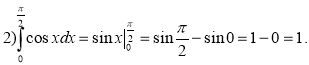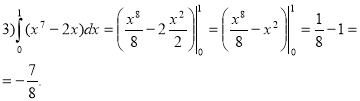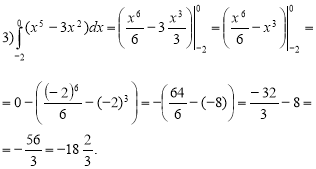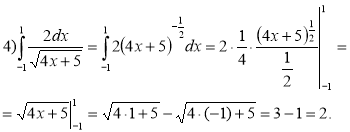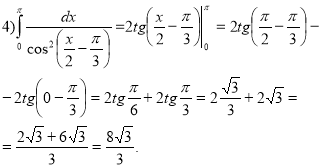Урок з теми " Формула Ньютона – Лейбніца. Основні властивості інтеграла”
Тема уроку: “ Формула Ньютона – Лейбніца. Основні властивості інтеграла”
Мета:
- навчальна:
ознайомити учнів з формулою Ньютона—Лейбніца та основними властивостями визначеного інтеграла, які випливають із властивостей первісної і формули Ньютона—Лейбніца; формувати вміння застосовувати дану формулу для обчислення визначених інтегралів; удосконалити вміння знаходити первісні для функцій;
- розвивальна:
розвити логічне мислення, пам'ять, увагу, спостережливість, вміння аналізувати, порівнювати, робити висновки; сприяти розвитку грамотної усної і письмової математичної мови;
- виховна:
виховати взаємоповагу в колективі, чуйне ставлення один до одного, вміння розуміти точку зору співрозмовника, визнавати право на іншу думку; прищепити інтерес до предмету.
Учні повинні:
- знати: формулу Ньютона – Лейбніца, основні властивості визначеного інтеграла;
- вміти: обчислювати визначені інтеграли із застосуванням формули Ньютона – Лейбніца, використовувати властивості визначного інтегралу при знаходженні визначених інтегралів.
Тип уроку: комбінований.
Хід уроку
- Організаційний момент.
Привітання. Організація класу до уроку. Перевірка присутніх учнів.
- Перевірка домашнього завдання.
- Мотивація навчальної діяльності.
«Недостатньо лише отримати знання,
треба їх систематизувати
і знайти їм гідне застосування».
Йоганн Вольфганг фон Гете.
(Німецький поет і
мислитель XVIII ст.)
На минулому занятті ми познайомились з поняттям визначеного інтеграла та з його геометричним змістом. Безпосередньо за означенням визначені інтеграли легко обчислювати лише для найпростіших функцій. Однак, для інших функцій, наприклад тригонометричних, обчислення границь інтегральних сум значно ускладнюється. До того ж такий спосіб потребує важких і громіздких обчислень. Сьогодні ми познайомимось з іншим способом обчислення визначених інтегралів значно простішим та легшим. Тому після вивчення сьогоднішньої теми ви зможете обчислювати визначені інтеграли та познайомитесь з його властивостями. Ці знання вам неодмінно знадобляться під час підготовки та складання Державної підсумкової атестації. Але, для того, щоб дізнатися тему сьогоднішнього заняття, вам необхідно пригадати деякий теоретичний матеріал, розгадати кросворд та знайти ключове слово.
- Актуалізація опорних знань учнів.
Фронтальне опитування
Кросворд
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Питання до кросворду:
- Як називається операція знаходження похідних? (Диференціювання)
- З якою величиною фігури пов'язаний геометричний зміст визначеного інтеграла. (Площа)
- Як називається функція F(х) для функції f (х) на деякому проміжку, якщо для будь-якого х із цього проміжку F' (х) = f (х). (Первісна)
- Як називаються числа а і b в позначені визначеного інтеграла. (Межа)
- Як називається операція, обернена до диференціювання. (Інтегрування)
- Як називається сукупність усіх первісних для даної функції f (х). (Інтеграл)
- Як називається фігура, обмежена графіком неперервної і невід'ємної на відрізку [а; b] функції у = f(x), відрізком [а; b] осі Ох і прямими x = а, х = b. (Криволінійна трапеція)
- Вивчення нового матеріалу
Отже, ви відшукали ключове слово теми сьогоднішнього уроку і це – «формула». Авторами формули, яка дає другий спосіб обчислення визначених інтегралів, стали два визначних вчених – англійський фізик, математик, механік і астроном Ісаак Ньютон і німецький філософ, логік, математик, фізик, історик Готфрід Вільгельм Лейбніц. Отже, тема сьогоднішнього уроку – «Формула Ньютона – Лейбніца. Основні властивості визначеного інтеграла».
(Доповідь учнів про життєвий шлях та наукову діяльність І. Ньютона і В. Лейбніца)
Формула Ньтона – Лейбніца
Якщо функція f(x) визначена та неперервна на відрізку [а; b] і F(x) — будь-яка первісна для функції f(x) на відрізку [а; b], то
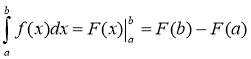 .
.
![]() - скорочений запис різниці F(b) - F(a).
- скорочений запис різниці F(b) - F(a).
Формула Ньютона-Лейбніца пов'язує поняття інтеграла й первісної для даної функції, і є правилом обчислення інтегралів.
Приклад 1. Обчисліть 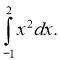
Розв'язання: Оскільки для функції f (x) = х2 однією із первісних є F(x) =![]() , то заданий інтеграл обчислюється безпосереднім застосуванням формули Ньютона – Лейбніца:
, то заданий інтеграл обчислюється безпосереднім застосуванням формули Ньютона – Лейбніца:
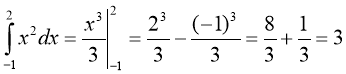 . Відповідь: 3.
. Відповідь: 3.
Приклад 2. Обчисліть 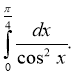
Розв'язання: Так як для функції f (x) =  однією із первісних є F(x) =
однією із первісних є F(x) =![]() , то маємо:
, то маємо: 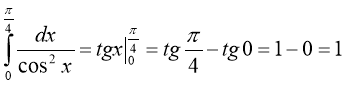 . Відповідь: 1.
. Відповідь: 1.
Із властивостей первісної і формули Ньютона-Лейбніца випливають основні властивості інтеграла:
-
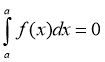 .
.
Доведення: 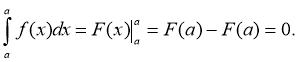
-
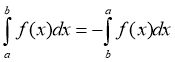 .
.
Доведення: 
- Постійний множник можна виносити за знак інтеграла:
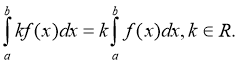
Доведення: Якщо F(х) є первісною для функції f(x), то для функції kf(x) первісною буде функція kF(х). Тоді
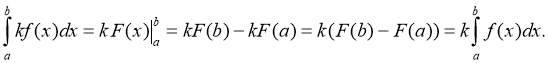
- Інтеграл суми (різниці) функцій дорівнює сумі (різниці) інтегралів :
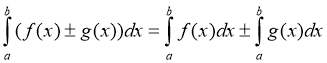 .
.
Доведення: Доведемо цю властивість для інтеграла суми функцій. Нехай F(х) – первісна для функції f(x), а G(х) – первісна для функції g(х), то для функції f(x) + g(х) первісною буде функція F(х) + G(х). Тоді
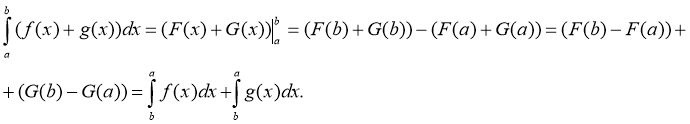 Аналогічно доводиться інтеграл різниці функцій.
Аналогічно доводиться інтеграл різниці функцій.
-
Якщо функція f (x) інтегрована на [а; b] і с
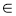 [а; b], то
[а; b], то
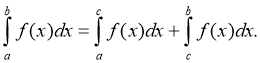
Доведення: Нехай F(x) — первісна для функції f(x). Тоді
 Додаючи почленно ліві і праві частини рівностей, одержуємо:
Додаючи почленно ліві і праві частини рівностей, одержуємо:
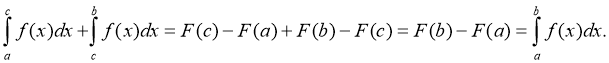
Приклад 3. Обчисліть 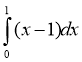 .
.
Розв'язання: Використовуючи властивості визначеного інтеграла (властивість 4), запишемо даний інтеграл як різницю двох інтегралів, кожний з яких безпосередньо можна обчислити за формулою Ньютона – Лейбніца:
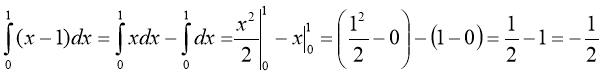 .
.
Відповідь: ![]() .
.
- Закріплення вивченого матеріалу. Формування умінь.
Виконання вправ
Завдання. Обчистити інтеграли (колективне розв’язання)
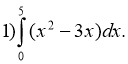
Розв'язання: Використовуючи властивість 4 визначеного інтеграла, запишемо заданий інтеграл як алгебраїчну різницю двох інтегралів. Для другого інтеграла, можна застосувати властивість 3 і винести постійний множник 3 за знак інтеграла. Кожний з отриманих інтегралів обчислюється за формулою Ньютона – Лейбніца:
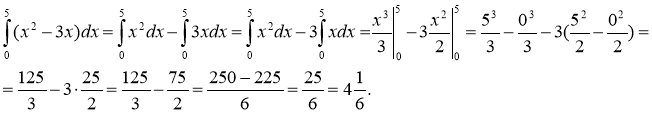 Відповідь:
Відповідь: ![]()
2) ![]()
Розв'язання: Використовуючи правила обчислення первісних і таблицю первісних, знаходимо первісну для функції f (x) =![]() . Потім знаходимо інтеграл за формулою Ньютона – Лейбніца:
. Потім знаходимо інтеграл за формулою Ньютона – Лейбніца:
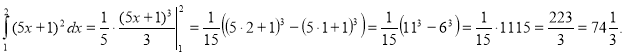
Відповідь: ![]()
3) 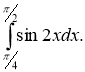
Розв'язання: Спочатку знайдемо первісну для функції f(x) =![]() , використовуючи правила обчислення первісних і таблицю первісних, а потім знайдемо інтеграл за формулою Ньютона – Лейбніца:
, використовуючи правила обчислення первісних і таблицю первісних, а потім знайдемо інтеграл за формулою Ньютона – Лейбніца:
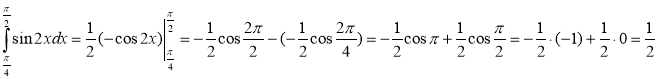 .
.
Давньогрецький поет Нівей говорив, що математику не можна вивчати, спостерігаючи, як це робить сусід. Тому зараз працюємо самостійно.
Самостійна робота
1 варіант
Завдання: Обчисліть інтеграл:
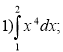
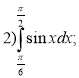
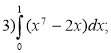
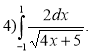
2 варіант
Завдання: Обчисліть інтеграл:
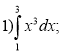
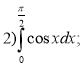
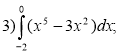
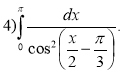
(Для перевірки самостійної роботи учні обмінюються своїми роботами один з одним. Вчитель оголошує відповіді до кожного завдання. Учні перевіряють відповіді та виставляють один одному оцінки).
Критерії оцінювання самостійної роботи: 1 завдання - 4 бали, 2 – 4 завдання - по 2 бали.
Розв’язання та відповіді до самостійної роботи
|
1)
Відповідь: |
Відповідь: 20. |
|
|
Відповідь: 1. |
|
Відповідь: |
|
|
|
|
Як вже було сказано, інтеграл має широке практичне застосовування. Розглянемо, як застосовують інтеграл під час розв’язування задач економічного змісту.
Завдання: Експериментально встановлено, що продуктивність праці робітника наближено виражається формулою f(t) = - 0,4t + 8, де t – робочий час у годинах. Обчислити обсяг продукції, виробленої за восьмигодинний робочий день.
Розв’язання: Питання до учнів:
- Що називається продуктивністю праці?( Продуктивність праці – величина, яка вимірюється кількістю продукції, випущеної працівником за одиницю часу.)
-
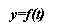

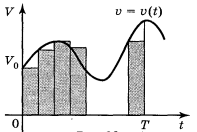 Як знайти об’єм випущеної продукції, якщо відома продуктивність праці та час, за який дана продукція була випущена? (Щоб знайти об’єм випущеної продукції, потрібно продуктивність праці помножити на час)
Як знайти об’єм випущеної продукції, якщо відома продуктивність праці та час, за який дана продукція була випущена? (Щоб знайти об’єм випущеної продукції, потрібно продуктивність праці помножити на час)
Нехай функція y = f(t) описує зміну продуктивності працівника за деякий робочий час. Знайдемо об’єм продукції V, виготовленої за проміжок часу [0, T]. Розіб'ємо проміжок часу [0;Τ] на n рівних частин точками
0 = t0 < t1 < t2 < ... < tn-1 < tn = Τ , ![]() ; t1 - t0 = t2 – t1 = …= tn – tn-1 = Δt.
; t1 - t0 = t2 – t1 = …= tn – tn-1 = Δt.
Тоді, об’єм продукції Vk , виготовленої за проміжок часу [tk; tk+1 ], де k = 0, 1, ..., n - 1 приблизно дорівнює добутку f(tk)·Δt, а об’єм всієї продукції, виготовленої за проміжок часу [0; Τ], приблизно дорівнює
![]() .
.
Якщо n → ![]() , то Δt → 0, і тоді об’єм продукції, виготовленої робітником за проміжок часу [0; T], який позначимо через V, дорівнює
, то Δt → 0, і тоді об’єм продукції, виготовленої робітником за проміжок часу [0; T], який позначимо через V, дорівнює ![]() . Отже, V =
. Отже, V = ![]() . Враховуючи означення визначеного інтеграла, отримаємо
. Враховуючи означення визначеного інтеграла, отримаємо 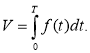
Тому 
Отже, за робочий день робітник виготовляє 51 одиницю продукції.
- Підсумок уроку.
Отже, сьогодні на уроці ми познайомились з властивостями визначеного інтеграла та навчилися обчислювати визначені інтеграли за допомогою формули Ньютона – Лейбніца.
Ми вже знаємо, що визначений інтеграл має велике практичне застосування. В першу чергу, з його допомогою можна обчислювати об'єми і площі поверхонь геометричних тіл, площі плоских фігур. Як саме це робити ми розглянемо на наступних заняттях.
Цікаво, що нікого не дивує, що математичну формулу для обчислення визначених інтегралів вивели фізик І. Ньютон і філософ В. Лейбніц, а це означає, що математика – мова, якою говорить сама природа.
- Домашнє завдання.
Мерзляк А. Г. Алгебра 11 кл: збірник задач і контрольних робіт № 223(1 – 12).
Література:
- Мерзляк А. Г. Алгебра 11 кл: збірник задач і контрольних робіт/А. Г. Мерзляк, В. Б. Полонський , Ю. М. Рабінович, М. С. Якір. – Х.: Гімназія, 2012.
- Нелін Є. П., Долгова О. Є. Алгебра і початки аналізу: дворівневий підруч. для 11 кл. загальноосвіт. навч. закладів. – 3 – тє вид., виправл. – Х: Світ дитинства, 2007.
- Шкіль М.І. Алгебра і початки аналізу 10-11 кл. [Текст] : підручник / М.І. Шкіль, З.І. Слепкань, О.С. Дубинчук – К. : Зодіак - ЕКО, 2002.
1


про публікацію авторської розробки
Додати розробку